
ジョン・マギーの投稿「 メルセンヌ・プライムスとルーカス-レーマー・テスト 」の翻訳。
記事のコードはここからダウンロードできます 。
出版の翻訳と準備の手助けをしてくれたPolina Sologubに深く感謝します。
内容
- はじめに。
- オイラーおよびメルセンヌの乗数定理
- ルークとレーマー
- から 前に
- 完璧な数字
-21、22、23番目のメルセンヌ数
-24、25、26番のメルセンヌ番号。
- 27日と28日のメルセンヌ
- 第29回メルセンヌ
- 30日と31日のメルセンヌ
- メルセンヌ番号の優れたインターネット検索
- メルセンヌ数の因数分解
はじめに
メルセンヌ素数は次の形式の素数です (次数pの値も単純でなければなりません)。 これらの素数は、17世紀前半にこの形式の素数のリストを作成したフランスの数学者および宗教学者メルセンヌに由来しています。 それらの最初の4つは長い間知られています。 、 、 そして 。
メルセンヌは 素数に対しては単純になります 多くに属する 。 彼がすべてについて正しかったかどうか、 Wolfram言語 -PrimeQ関数を使用して確認できます 。これは、数字を合成することを証明するために特定の要因を検索する必要がない、簡単にするために数字をテストする最新の方法を使用します。


彼の声明は -素数、単なるタイプミス、そして実際には彼は 。 核分裂テストは利用可能な数少ないツールの1つであるため、メルセンヌの生涯の間に単純性のチェックが困難であったことは容易に理解できます。 たとえば、 最小のファクターは15桁の数値であるため、最新の因数分解法を使用してもそれほど簡単に見つけることはできません。 FactorInteger関数は、分解法を大きな整数に適用できる最も高度な方法を使用します。
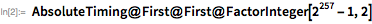

オイラーおよびメルセンヌの乗数定理
シンプルテストの分野における最初の重要な成果は、偉大な数学者レナード・オイラーに属します。 簡単です。 彼は、単純な除数 1または62(mod 248)に等しくなければなりません。
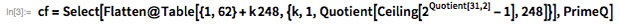

このような比較的短いリストは、オイラーの時点でさえ、(手動で)試行分割を使用して確認できます。 彼はメルセンヌの定理の適用に属します。 仕切りです それから 、 そして 正の整数の場合 。 これらの事実により、可能な除数の数が大幅に制限されます。 。 以下の関数を使用して、この定理を使用して可能な除数のリストを提供する方法を示します より小さい 。
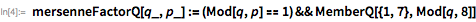
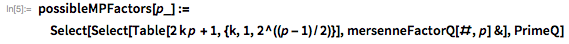


これらの機能を使用して、除数をすばやく見つけます。 。 ご注意ください 仕切りです 場合にのみ 。 これにより、効果的な累乗法を提供するPowerMod関数を使用できるようになります。
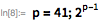
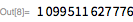


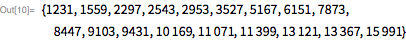

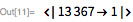
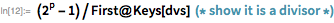
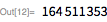
以下は、161649文字のメルセンヌ数です。


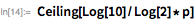


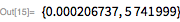
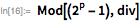

ルークとレーマー
次の重要なステップは、 Eduard Lukeによるこの形式の数字の単純さをチェックする方法の発見でした。 彼は1876年に彼の方法を使用して、 (「プレコンピューター」時代の最大のメルセンヌ数)は単純です。 20世紀の初め、二項算術と代数の基礎が広く知られるようになったとき、 デレクヘンリーレマーはルークの方法を完成させました。 結果として得られたLuc-Lemer数の単純性テストは 、この形式の数が素数であるかどうかの効果的なチェックを提供しました。 チェックは、モジュロの比較を使用して実行されました。

つまり、 によって表される数と同一 下位ビットに加えて、残りのビットで表される数値。 この比率は、次の限り再帰的に適用できます。 。
次の例を考えてみましょう。 ここでそれを示します
 のために 。 ご注意ください
のために 。 ご注意ください  (23下位ビット)および
(23下位ビット)および  -残りのビットが最下位にシフトされることを意味します。
-残りのビットが最下位にシフトされることを意味します。


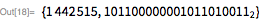
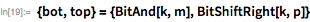



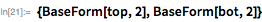
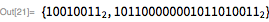

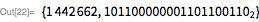
以下の関数は、この計算方法を定義します ビット演算のみを使用します(除算なし)。 ご注意ください バイナリ形式を持っています 、単一の0はありません。したがって、 数値の下位ビット 。

次の関数は、Luc-Lemer単純性テスト(LLT)を実装します。 シーケンスを定義する 、 。 それから 場合にのみ 。

経験上、これらの関数にかかる時間のほとんどは整数演算に費やされることが示されています。
かどうかを確認するには シンプルな場合、最初に小さなシンプルな仕切りでシンプルさをテストし、他のシンプルさチェックを実行するのが最善です。 まずcheckMPDivisorsでエンコードされたメルセンヌの素数の除数定理を使用し、次にPrimeQ関数を使用します。 これが機能しない場合は、Luc-Lemerテストを適用します。

ここでは、 PrimeQ関数の拡張バージョンを紹介します。これは、多数のフォームに対してLuc-Lemerテストを適用します 。

から 前に
Luc-Lemerテストを使用してコンピューターで見つかった最初のメルセンヌ素数は 、ランプコンピューターSWAC(Standards Western Automatic Computer)に基づいて1952年1月30日にRafael Robinsonによって発見されました。 以下に、それぞれ37ビットの256ワードを含むこのコンピューターのメモリブロックを示します。

20番目のメルセンヌ素数は、IBM 7090での50分間のLuc-Lemerテストの結果として、1961年11月にAlexander Hurwitzによって発見されました。







この種の作業に適したWolfram言語の機能の1つは、高速整数演算です。 メルセンヌ素数の検索は、コンピューター化された検索の時代のd明期に大きな課題になりました。 研究者は、高速フーリエ変換法を採用して、2つの大きな整数を乗算するタスクを、変換された数字の単純な要素単位の積に変換しました。 整数の素早い乗算は、Luc-Lemerテストの2乗ステップに必要です。 Wolfram言語は数十億文字の正確な整数で動作するように最適化された最新のアルゴリズムを使用しています。 たとえば、最後のものが 、実際には素数のメルセンヌ数であり、そのすべての数を示しています。



完璧な数字
メルセンヌ素数と完全数の間には興味深い関係があります。 完全数とは、そのすべての約数の合計に等しい数です(数自体を除く)。 ユークリッドは仮定し、オイラーはすべての完全な数が次の形式であることを証明しました 。 Wolfram言語のPerfectNumberQ関数は、数値が完全かどうかをチェックします。 このプロパティのデモを行います 。
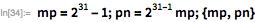

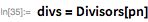


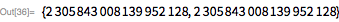


21、22、および23メルセンヌ
21番、22番、および23番のメルセンヌ数の再発見に進みます(さらに、次の形式で示します)。 ): 、 、 。 それらはすべて、ドナルドギリスによって発見されました。ドナルドギリスは、1963年春にイリアックIIでLLTを開始しました( こちらを参照)。 フォームのすべての番号を確認するには 間の素数の場合 約6分かかりました。


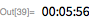
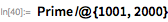
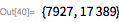

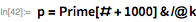



24、25、26番目のメルセンヌ数
次に、検索を展開して見つけます 、 、 。 これらの最後のものは1979年2月にランドン・カート・ノールとローラ・ニッケルによって発見されました。 彼らは 前に CDC Cyber 174スーパーコンピューター上で(これについてはこちらをご覧ください )。 計算が長くなっているため、並列処理を使用し始めています。 テストは独立しているため、 ParallelMapを使用して作業を高速化できます。 範囲チェック 約3分半かかります(4つのコアが使用されます)。



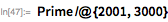
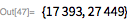


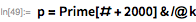
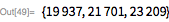
特化されたLuc-Lemerテストは、より一般的なPrimeQ関数(指定されたメルセンヌ数)よりもはるかに高速であることに注意してください。

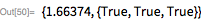
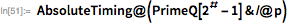

27日と28日、メルセンヌ
次に、範囲を確認しました 番号を見つける 。 それは1979年4月にハリー・ネルソンと彼のチームによって発見されました(彼らはCray-1スーパーコンピューターを使用しました)。 検索は15分で完了しました。


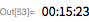
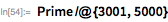


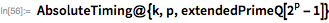
次のメルセンヌ数、 。 1982年9月にDavid Slowinskiによって-これもCray-1で開かれました。 このスーパーコンピューターの重量は約5トンで、約115キロワットの電力を消費し、そのコンピューティングパフォーマンスは160 メガフロップに達しました 。 100万個の64ビットメモリワード(8メガバイト)が付属し、現在の価格では約1,600,000ドルかかりました。 以下は、その冷却システムの詳細です。 比較のために: Raspberry Piの重さは数オンスで、4ワットで動作し、約410メガフロップスを提供し、1GBのRAMを搭載しています。これはすべて40ドルです。 Mathematicaにもすぐに付属しています。


数 25962桁が含まれます。 この値は1時間14分で(Raspberry Piではなくラップトップで)検出され、範囲でテストされました 。








第29回メルセンヌ
現在、より深刻なコンピューター時間が必要なので、実行ごとにタイムスタンプも生成します。 次に範囲を確認します 。 1時間44分後に、コンピューターは以下を示しました。 。 この番号は、1988年1月29日にWalker ColquittとLuke Welsh(NEC DX-2スーパーコンピューター。記事はここにあります )によって最初に発見されました 。






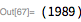




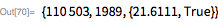


30日と31日のメルセンヌ
次の2つのメルセンヌ素数: そして 、-は実際に29日以前に発見されました(28日を発見した同じチームによって)。 彼らはCray X-MPを使用して、1983年9月に30番目のメルセンヌ数を、1985年9月に31番目を見つけました。 確認する 範囲検索機能を使用する 。 それぞれを確認するには この範囲では、4時間8分かかりました。








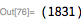

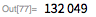



グレートインターネットメルセンヌ数検索
34番目のメルセンヌ素数の発見により、 -1996年9月、メルセンヌ素数を検索するためのスーパーコンピューターの時代は終わりました。 次の15個は、グレートインターネットメルセンヌシンプルナンバーサーチ( GIMPS )のボランティアによって発見されました。これは、パーソナルコンピュータで(バックグラウンドプロセスとして)Luc-Lemerテストのバリアントを実行します。 この大規模な分散コンピューティングプロジェクトは、現在、1秒あたり約300テラフロップスに相当するパフォーマンスレベルを達成しており、アイドル時間は130万台を超えています。

Luc-Lemerテストを使用して、34番目のメルセンヌ数を確認しましょう。 この段階で、パソコンの機能の限界に達しました。 この範囲で数千のメルセンヌ数をテストするには、何日もかかります。 1つの大きな素数をテストするために必要な数十億の計算の中で1つの算術エラーが誤った結論につながり、損失を意味するため、Luc-Lemerテストはコンピューターハードウェアおよびソフトウェアの信頼性のストレステストとしてよく使用されることに注意してくださいメルセンヌ数または間違った答え。 それぞれを確認したという事実 2から139901までの素数の場合、MathematicaシステムとWolfram言語での多数の算術演算と2項演算の信頼性を説得力をもって証明します。
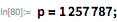


メルセンヌ数の因数分解
すでに見てきたように、フォームの数の拡大で考えられる要因の数 メルセンヌ乗数の定理によれば、それは有界です。 これにより、この形式の大きな除数の効率的なコンピューター検索が可能になりました。 この記事の執筆時点では、すべてのメルセンヌ数( )完全に因数分解されました(図はここにあります )。 GIMPSプロジェクトは、単純な数字の検証の副産物として、多くのメルセンヌ数の大きな乗数の発見にもつながりました。 この問題を解決するための最新のアプローチである新しい記事(および17の新しい因子分解)は、 ここにあります 。 最大の因数分解された数は ; 見つかった最小の除数は10進数で76桁です。 最小の除数は23です。この結果を得るのに必要な合計時間は7500年です(コンピューター時間について)。
最初のいくつかの要因をすばやく見つけることができます。 FactorInteger関数を使用します。


これまでに発見されたすべてのメルセンヌ素数は、Wolfram言語でカタログ化されています(44日まで)。 この情報へのアクセスは、 MersennePrimeExponentおよびMersennePrimeExponentQ関数によって提供されます。
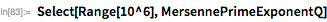





このトピックに興味がある場合は、次のWebサイトで詳細を確認できます。