サッカーボールとフラーレン

最も美しい数学的結果の1つは、安全にオイラーの定理と考えることができます。これは、ペテルスブルグ科学アカデミーのレナードオイラーの作品「身体の教義の要素」および「平らな顔に囲まれた身体が対象となるいくつかの注目すべき特性の証明」に初めて登場しました。



オイラーの定理。 させる $$${\ rm B}$ -凸多面体の頂点の数、 $$${\ rm P}$ エッジの数と $$$\ガンマ$ -顔の数。 それから平等

$$

$${\ rm B}-{\ rm P} + \ガンマ= 2$$

数 $$$\ chi = {\ rm B}-{\ rm P} + \ガンマ$ 多面体のオイラー特性と呼ばれます。 慣れ親しんでいる一部の多面体のオイラー特性を計算するのは簡単です。

多面体	$$${\ rm B}$	$$${\ rm P}$	$$$\ガンマ$	$$$\ chi$
四面体	4	6	4	2
キューブ	8	12	6	2
八面体	6	12	8	2

オイラーの定理の証明はここにあります 。

オイラーの定理を使用して、いくつかの興味深い事実を確立しましょう。 サッカーボールの画像を見てください。

質問：ボールを縫うには五角形がいくつ必要ですか？ させる $$$x$ -六角形の数、および $$$y$ -五角形の数。 オイラーの定理をサッカーボールに適用してみましょう。

$$

$${\ rm B}-{\ rm P} + \ガンマ= 2、$$

どこで $$${\ rm B} = \ frac {6x + 5y} {3}$ 、 $$${\ rm P} = \ frac {6x + 5y} {2}$ 、そして $$$\ガンマ= x + y$ 。 頂点、エッジ、および面の数の式は、各頂点が3つの面に該当し、各エッジで2つの面のみが交差するという観察から簡単に得られます。 数式の値を代入すると、答えが得られます。 $$$y = 12$ 。 可変 $$$x$ 方程式から除外、すなわち 六角形の数は何でもかまいません。 次の画像は、五角形だけで作られたボールを示しています。 それらのいくつ？

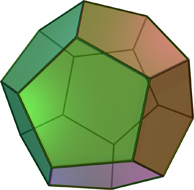
この多面体は12面体と呼ばれ、5つの正多面体の1つです。

別のプロットを見てみましょう。 フラーレンは、同素体の炭素のクラスに属する分子化合物であり、偶数個の三配位炭素原子で構成された凸閉多面体です。 フラーレンの名前は、この原則に基づいて測地構造が構築されているエンジニアおよび建築家のリチャード・バックミンスター・フラーに由来しています。 当初、このクラスの化合物は、五角形と六角形の面のみを含む構造に限定されていました。

最後に、次の図を見てみましょう。

特別なものはありません-六角形から組み立てられたドームだけです。 そして、オイラーの公式をもう一度瞑想し、五角形を探しに行きます。

アレクセイ・サヴァテエフの注目すべき講義または彼の著書 「数学のための数学」で、これと他の多くの数学的主題を参照してください。