A new solution to the Fermi paradox (why we are alone in the universe)
Recently I came up with a completely new solution to the Fermi Paradox . I will not retell what you can read on the wiki.
I will pass to the point. To solve the problem, we need a few ingredients.
A fairly well-known and explained (often incorrectly) popular science thing. Briefly, in the MWI the world is “entirely” determined, there is no accident. When events have several outcomes, they all happen, and then, using the decoherence mechanism, different “branches” of reality appear in our macro-world, where different copies of our consciousness fail. However, each copy considers itself unique, since there is no interaction between branches.
The interesting and controversial idea of quantum suicide is based on MWI. Say, if the shot of the gun will depend on the quantum event, then having put such a gun to the head we don’t lose anything: in the branch where the gun fired, we will cease to exist, and where we didn’t shoot, we continue to exist. That is, our consciousness "falls" into the branch where the shot did not happen.
Quantum suicide is often criticized for the following reason - what if death from a shot is not instant? But what if we do not die, but remain paralyzed? Below we will return to this issue.
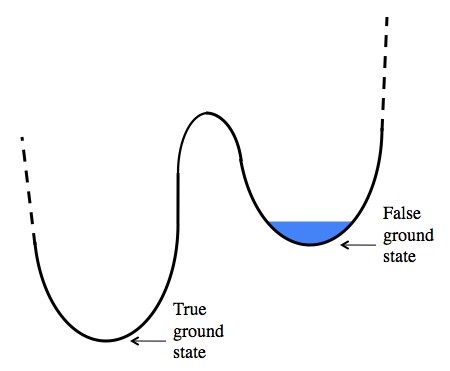
It is possible that our vacuum is false , that is, our void is not a lower state of vacuum (in the energy sense). Then a spontaneous transition at some point in the vacuum into a more favorable energy state is possible. The difference in the energy of the vacuum turns into a mess of a variety of particles (and possibly not existing in our vacuum), and their number is huge. Actually, the matter that existed before such an event can be neglected.
Further, when the center of destruction arose, it is impossible to stop the process, like dominoes, the process spreads in all directions, and at the speed of light! That is, he has no harbingers - not even disturbing music, like in films. You sit, drink wine at night and look at the stars, and then once - and there is nothing but a plasma of new particles.
We would like to believe that such an event is very very very unlikely, for example, Nick Bostrom answered me with a link to his article with Tegmark, where they estimated the probability of such an event "from above":
arxiv.org/abs/astro-ph/0512204
Have you noticed that vacuum catastrophe is much better suited for quantum suicide than a gun? The process is instant, it cannot leave you crippled ... It is just perfect. And so ... What if it happens regularly, but we don’t notice it? I would like to consider just such a universe.
Let's introduce the value D (doom factor), which is proportional to the probability of spontaneous decay of the vacuum. For D = 1, one such event occurs once a year in a 1x1x1 light-year cube. Astronomers are now cringed at using the light year as a measure of distance, instead of the parsec, but in this case I really want to measure time and distance in "identical" units.
So, what is the likelihood that we will remain alive in such a universe? We need to estimate the number of potential disasters in the past, that is, in our past light cone. This value is equal to the four-volume of a 4-dimensional cone of height t if the distances are measured in light years and time is simply in years (c = 1):
For our history, the time in this formula must be replaced by A = 13.8 billion years - the age of the Universe. (in fact, this is not entirely honest, since closer to the time of the Big Bang, the cone is distorted due to GR, but we ignore these effects here)
Asking
we get n = 379 million. That is, the probability that we did not die is equal 
. This should not surprise us, in the MWI the branches are separated even more even within minutes and seconds.
Nevertheless, it is interesting to trace, and when (on average) was the last event of this kind? This can be done by the formula:
The value that we get is rather strange (for our random choice D) - about 100 million years. However, in fact this is not surprising, since the 4-volume of the cone grows very quickly to the base. That is, the danger that lies in wait for us does not come from the vacuum that accidentally collapsed 4 years ago at Alpha Centauri, but that it will be covered by a wave of decomposition that has reached us from the far depths of the Universe.
For estimation, we take the derivative of n with respect to t and obtain:
For our value of D, the value of n increases by 0.11 every year, that is, roughly speaking, every 9 years our chances are reduced by half (but, again, we do not notice this at any value of D!)
Again, I will not retell the wiki . However, this argument operates with (poorly defined) statements about 'souls' that 'infuse' (temporally) randomly into the bodies that are available. Since bodies are much larger by the end of civilization, the probability of being born in the Roman Empire is very small.
However, if the number of bodies is normalized by the probability of the existence of branches of reality (and it should normalize in this way - the Bourne rule would not work otherwise), then the “corrected” distribution of the number of bodies has a peak at the beginning of time and not at its end, that is, it inverts this argument:
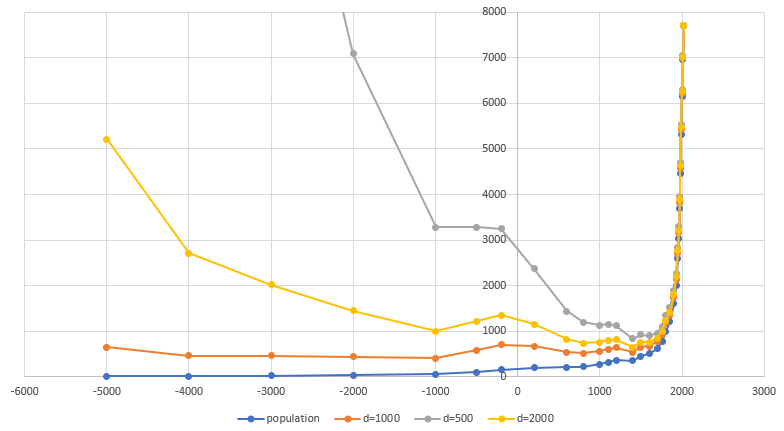
The blue line on the graph shows the world's population in millions of people at different times. Other curves 'normalize' these values taking into account that the probability amplitude in the past was greater (for smaller values of D, for example, d = 1000 - the probability decreases by half in 1000 years, and not 9 years)
Finally, we come to the paradox itself. We apply the inverted doomsday argument to civilizations (moreover, when the development time of different civilizations diverges in millions of years, the effect begins to appear from much lower D values). That is, the probability of being born in late civilization is negligible.
That is, we were born in the first, and so far the only civilization!
The wiki article provides various solutions to the problem. Vote for those that you think are likely. I took the options from the English version of Wiki (there are few of them in the Russian version), but I combined some
I will pass to the point. To solve the problem, we need a few ingredients.
1. MWI - the interpretation of the multiverse.
A fairly well-known and explained (often incorrectly) popular science thing. Briefly, in the MWI the world is “entirely” determined, there is no accident. When events have several outcomes, they all happen, and then, using the decoherence mechanism, different “branches” of reality appear in our macro-world, where different copies of our consciousness fail. However, each copy considers itself unique, since there is no interaction between branches.
2. Quantum Suicide
The interesting and controversial idea of quantum suicide is based on MWI. Say, if the shot of the gun will depend on the quantum event, then having put such a gun to the head we don’t lose anything: in the branch where the gun fired, we will cease to exist, and where we didn’t shoot, we continue to exist. That is, our consciousness "falls" into the branch where the shot did not happen.
Quantum suicide is often criticized for the following reason - what if death from a shot is not instant? But what if we do not die, but remain paralyzed? Below we will return to this issue.
3. Vacuum Catastrophe (decay of false vacuum)
It is possible that our vacuum is false , that is, our void is not a lower state of vacuum (in the energy sense). Then a spontaneous transition at some point in the vacuum into a more favorable energy state is possible. The difference in the energy of the vacuum turns into a mess of a variety of particles (and possibly not existing in our vacuum), and their number is huge. Actually, the matter that existed before such an event can be neglected.
Further, when the center of destruction arose, it is impossible to stop the process, like dominoes, the process spreads in all directions, and at the speed of light! That is, he has no harbingers - not even disturbing music, like in films. You sit, drink wine at night and look at the stars, and then once - and there is nothing but a plasma of new particles.
We would like to believe that such an event is very very very unlikely, for example, Nick Bostrom answered me with a link to his article with Tegmark, where they estimated the probability of such an event "from above":
arxiv.org/abs/astro-ph/0512204
Doom Factor.
Have you noticed that vacuum catastrophe is much better suited for quantum suicide than a gun? The process is instant, it cannot leave you crippled ... It is just perfect. And so ... What if it happens regularly, but we don’t notice it? I would like to consider just such a universe.
Let's introduce the value D (doom factor), which is proportional to the probability of spontaneous decay of the vacuum. For D = 1, one such event occurs once a year in a 1x1x1 light-year cube. Astronomers are now cringed at using the light year as a measure of distance, instead of the parsec, but in this case I really want to measure time and distance in "identical" units.
Doomed Universe
So, what is the likelihood that we will remain alive in such a universe? We need to estimate the number of potential disasters in the past, that is, in our past light cone. This value is equal to the four-volume of a 4-dimensional cone of height t if the distances are measured in light years and time is simply in years (c = 1):
For our history, the time in this formula must be replaced by A = 13.8 billion years - the age of the Universe. (in fact, this is not entirely honest, since closer to the time of the Big Bang, the cone is distorted due to GR, but we ignore these effects here)
Oh lucky one!
Asking
we get n = 379 million. That is, the probability that we did not die is equal . This should not surprise us, in the MWI the branches are separated even more even within minutes and seconds.
Nevertheless, it is interesting to trace, and when (on average) was the last event of this kind? This can be done by the formula:
![$ h = \ sqrt [4] {\ frac {3} {\ pi D}} $](https://habrastorage.org/getpro/habr/formulas/423/f2d/63f/423f2d63fe078d5ecab8428fc6cac8f3.svg)
The value that we get is rather strange (for our random choice D) - about 100 million years. However, in fact this is not surprising, since the 4-volume of the cone grows very quickly to the base. That is, the danger that lies in wait for us does not come from the vacuum that accidentally collapsed 4 years ago at Alpha Centauri, but that it will be covered by a wave of decomposition that has reached us from the far depths of the Universe.
How quickly do we decompose?
For estimation, we take the derivative of n with respect to t and obtain:
For our value of D, the value of n increases by 0.11 every year, that is, roughly speaking, every 9 years our chances are reduced by half (but, again, we do not notice this at any value of D!)
Doomsday Argument
Again, I will not retell the wiki . However, this argument operates with (poorly defined) statements about 'souls' that 'infuse' (temporally) randomly into the bodies that are available. Since bodies are much larger by the end of civilization, the probability of being born in the Roman Empire is very small.
However, if the number of bodies is normalized by the probability of the existence of branches of reality (and it should normalize in this way - the Bourne rule would not work otherwise), then the “corrected” distribution of the number of bodies has a peak at the beginning of time and not at its end, that is, it inverts this argument:
The blue line on the graph shows the world's population in millions of people at different times. Other curves 'normalize' these values taking into account that the probability amplitude in the past was greater (for smaller values of D, for example, d = 1000 - the probability decreases by half in 1000 years, and not 9 years)
Fermi paradox
Finally, we come to the paradox itself. We apply the inverted doomsday argument to civilizations (moreover, when the development time of different civilizations diverges in millions of years, the effect begins to appear from much lower D values). That is, the probability of being born in late civilization is negligible.
That is, we were born in the first, and so far the only civilization!
Poll
The wiki article provides various solutions to the problem. Vote for those that you think are likely. I took the options from the English version of Wiki (there are few of them in the Russian version), but I combined some
All Articles