カットの下-詳細なテキストデコードとほとんどのスライド。

私の報告は最も標準的なものではありません。 残念ながら、列挙子の組み合わせはあまり真剣に研究されていません-ロシアでは標準的な大学プログラムに含まれていません。 レポートの最初の入門半分では、列挙型組み合わせ論からの有名な古典的な質問を引用します。 後半では、最近気づいたものからさらに複雑なものになります。 あなたが私を止めて質問した場合-それは大丈夫です。
列挙組み合わせ論とは何ですか? 通常、自然数のシーケンスを研究します。 彼らは違います。 Online Encyclopedia of Integer Sequencesから半ダースのシーケンスを書きました。 ロシア語を話しますが、スライドはすべて英語です。
いくつかのシーケンスはよりコンビナトリアルであり、いくつかはより少ない組み合わせです。 たとえば、この百科事典の最初のシーケンスである有限グループの数は、あまりコンビナトリアルではありません。 次数4の2つのグループがあることがわかります。次に簡単なシーケンスは素数です。 整数nのパーティションの数、項の合計-後で確認します。 次のシーケンスはフィボナッチ数列です。 次に、インボリューションの数、カタロニア語の数、接続されたグラフの数。
質問は次のとおりです。各シーケンスの数値を記述する式はありますか? これは難しい質問です-それは式の意味に関連しています。 さまざまなシーケンスと式について説明します。 それから私はそれを統一して、理論を伝えようとします。 シーケンスを研究し、それらに含まれる数値の公式を理解しようとします。

標準の紹介から始めます。 私自身は何も決定しません-2人の著者を引用する方が良いです。 最初の引用はリチャード・スタンレーによるもので、長い間読んでいますが、その意味は次のとおりです。彼は、「何かが何かを掛けたものの合計に等しい」と書けば、最も興味深いのは明示的な式だと考えています。
ハーブウィルフは、式はこれが和であるか積であるかには関係なく、そのように定義することはできず、式は実際にはアルゴリズムであるとは言いません。 私たちにとって、彼のアイデアは非常に重要です。 数式は、nの時間多項式のシーケンス内の数をカウントする特定のアルゴリズムです。
しかし、実際には、古いアイデアは、式が良いかどうかを理解することです。 彼らは漸近式で式を見ます。 この数値がプラスまたはマイナス3%の精度で式によって理解できる場合、これは適切な式です。 フォーミュラとは何かの3つの標準定義をリストしました。 3つすべてが非常に重要になりますが、アルゴリズムのアプローチが最も重要になります。

漸近線から始めましょう。 これは非常に古いもので、すべてのシーケンスで知られています。 たとえば、フィボナッチ数は非常に特定の指数関数的方法で成長し、カタロニア語数も指数関数的に成長します-多項式因子があります。 非常に古い定理について話している。 これは、100年以上前の素数分布定理です。 パーティションの数については、驚くべき漸近式もあります。 証明するのはそれほど簡単ではありませんが、指数項の理解は少し簡単です。
退縮の数については、複雑すぎず、少しの分析が必要です。 しかし、次数<= nのグループ数の式は非常に複雑です。 それを証明するには、単純な有限群の分類を知る必要があります。これは完全な組み合わせ論ではなく、組み合わせ論ではありません。
しかし、最後の式はそれどころか非常に単純です。 n頂点のグラフの数は、度(...)係数で約2、n / 2です。 また、その意味は非常に単純です。ランダムグラフは、nが無限大になると1になる傾向の高い確率で接続されます。
これらの式は優れていますが、組み合わせ式ではなく分析式です。 また、これらの数値をカウントする方法を理解することはできません。 そして、これが私たちのすることです。 そして、私たちが何をしているかを正確に理解するために、非常に標準的な古典的な例であるフィボナッチ数から始めます。

それらの定義の1つを示します。 フィボナッチ数は、2つの連続した単位がない長さnから1を引いた0と1のシーケンスの数です。 たとえば、2つのユニットが連続しない長さ2のシーケンスが正確に3つあります。ここでは、00、01、10です。2つのユニットが連続しない5つの長さ3のシーケンスがあります。
以下の3つの式があります。 最初の式は、私たちから繰り返されるフィボナッチ数の比です。次は、前の2つの値の合計です。 2番目の式は、フィボナッチ数を二項係数の合計として書き出します。 3番目の式は非常に明確です。彼女は、それらを黄金比とその逆の2度の合計として記述します。
次の質問は、これらの式のどれが良いですか? 学生、新入生、2年生を教えるとき、私は伝統的に最初の式から始めます-これは定義であると言い、しばらくして3番目の式を導き出し、30分を証明します。
しかし、117番目のフィボナッチ数を計算する必要がある場合、3番目の式はまったく役に立ちません。 それを計算するには、このゴールデンセクションが正確に何であるかを非常に明確に知る必要があります-多数の記号でカウントする必要があります。 そして、これもまた困難です。 どうしますか? 考えてみると、これは良い方法ではありません。 二項係数の合計の式は優れていますが、計算の場合、最初の式の方がより簡単で簡単です。 あなたは一つずつ数え、すべてがうまくいくでしょう。
問題が何であるかはすでに明らかです。 どちらの式が優れているかは完全には明らかではありません。 美学の観点からは、おそらく3番目の式の方が優れており、漸近性の観点からは確かです。 彼女はすぐにフィボナッチ数が漸近的であると言います。 ただし、最初の式は計算に適し、2番目の式はいくつかの定理を証明するのにより適しています。

暴動の数は非常に古いシーケンスです。 要素iが常にiに等しくない要素に入るような順列の数を取ります。 長さ2の順列がある場合、そのような順列は常に1つだけです。 単一の順列は適合せず、{21}が適合します。 長さ3の順列がある場合、両方ともループである正確に2つの順列があります。 残りはまったく適合しません-それらには固定点があります。
そして一般的に、再び3つの式。 最初は素晴らしいです:この数はn!/ Eに最も近い整数です。 非常に単純な式があります。 シンプルだが漸近的な成果は驚くべきものです。 eの値をコンピューターで計算するのは非常に難しく、長さ117の暴動の数を明示的に計算するには、非常に高い精度でeを知る必要があります。 2番目の式は最初の式を説明しています。 大まかに言えば、nを取り出すと! アウト、nを取得! テイラー級数の最初のkメンバーの合計を掛けます。 一方では、これは最初の式を説明し、他方では、ここに整数があります-それらは簡単に明示的に計算できます。
実際、最適な計算式は3番目です。 わずかに予期しない再帰関係が得られますが、これは最も簡単に計算でき、まったく何も説明しません。 定義からそのような式を証明することは、非常に明白な練習ではありません。 これ(–1)のn乗をどう処理するかは明確ではありません。 これが物語です。 暴動の数については、どの式が良いのか、どの式が悪いのかが明確でないことは明らかです。

メナージュ番号、フランス語。 タスクは次のとおりです。19世紀の昔ながらのディナーパーティーが開催され、n人のカップルが招待され、2つの条件が満たされるようにすべてを植えたいと考えています。 最初の条件は、男性が女性と交互になることです。 2番目の条件は、配偶者が隣同士に座っていないことです。 XIX世紀の仕事は、おそらく誰かがまだそのようなディナーパーティーを収集しています。 彼らは結婚式でそれをするという。
この数を計算する方法は? 結婚しているカップルが2人しかない場合、それらを座らせることはできません。 カップルが一緒に座るために、彼らはお互いに反対でなければなりません-それは交替がないことを意味します。 夫婦が2人いる場合、シーケンスは最初から始まります。 しかし、結婚した夫婦が3人いるときは、すでにかなりの数のこのような座席の配置があります。 ここにそれらの1つがあります。 カップル1A、2B、3Cがあるとします。 A、B、Cは順番に植え付けを行い、1、2、3はより複雑な方法で植えます。 3はAとBの間にあり、AまたはBの配偶者ではないことがわかります。
この問題は解決できます。 歴史的な観点から、2つの解決策があります。 最初の-複雑で、長く、再帰的-は、1891年に以前に取得されました。 2番目の解決策は、二項係数、階乗、因子などの合計の明示的な式です。この比率が得られたとき、誰も特に満足していませんでした。 これに従ってすべてを計算するのは簡単ですが、これはあまり必要な式ではないと考えられていました。 しかし、1934年にタシャードが二項係数の変数和の形式で式を受け取るとすぐに、誰もが問題が解決したと考えました。 計算の観点からは、2番目の式の方がはるかに優れています。
周期的組み合わせ論からの非常に古典的な例を挙げます。 これをどのように使用しますか? 現在、明示的な式が何であるかについての理解を改善しようとしています。 標準的な方法は、生成関数を取得することです。 これを行うには、2つの異なる方法があります。 最も簡単な方法は、単純にそのようなシリーズの合計を取り、tの正式な関数と見なすことです。

問題は、この関数の式があるかどうかです。 多くの場合、シーケンスには適切な式はありませんが、関数にはあります。 ここに、フィボナッチ数の非常に良い式がある例があります-生成関数にとって非常に合理的です。 しかし、カタロニア語の数については、n + 2ゴンの三角形分割の数が使用されます。 オイラーは1750年代にサンクトペテルブルクでそれらを発明し、研究しました。 この場合の生成関数は合理的ではなく、代数的です。

他の例を見てみましょう-退縮の数を言う。 インボリューションは、2乗が1に等しい順列です。 これは、1または2の長さのサイクルで構成されることを意味します。このようなインボリューションの数については、これを二項係数の合計として表すことができる適切な式はありません。 ただし、非常に良い再発率があります。 これを証明する方法は明らかですか?
nの最後の要素を取得します。 固定小数点-順列の数が1少ないか、他の要素と転置されているかのいずれかです。 そのような要素を選択する方法はn-1個あり、その後に何かを行う必要がある要素がn-2個あります。 定義から、このような単純な再帰関係が得られます。 それはあなたが明示的に書くことができる素晴らしい生産機能を持っています。 これは指数生成関数であることに注意してください。 t n > a n / nを取ります! -確率の生成関数を見ているかのように。
そして、ここには良い式e t + t 2/2があります。
明示的な式を見る新しい方法があります。 パーティションの数nについて、nを被加数の合計として表すいくつかの方法があります。 たとえば、4 = 3 + 1 = 2 + 2など-4を項の合計として記述する方法は5つあります。 しかし、プロデュース機能も素晴らしいです。 オイラーも1738年にこれを思いつきました。 無限の仕事はそれがどうなるかです。 これは前に見たほど良い機能ではありません。 無限の作業がある場合、それをどうするかはあまり明確ではありません。 かなり複雑な機能です。
-カウントについて教えてください。
-n個の頂点にある接続されたグラフの場合、再帰関係がありますが、それは二次関数であり、その係数は二項になります。 グラフには2次の関係がありますが、心から覚えていません。 すぐにカウントできますが、このトピックには含まれていません。

理論 できるだけ多くのシーケンスを分類したいと思います。 いくつかのクラスを取ります。 最初のクラスは有理数列です。 生成関数が有理である場合、つまり、2つの多項式の比率である場合、それらは有理です。 実際、これは、フィボナッチ数を一般化する、指定された数の単純な繰り返し関係と完全に同等です。 ここにあなたが考えることができる最も簡単なものがあります。 驚くべきことに、これらの再帰関係を満たすシーケンスはかなりあります。 ただし、シーケンスは有理関数よりも単純です。 すべての有理数列には非常に単純な漸近線があり、非常に簡単に学習できます。
次のレベルは代数です。 これらは、数式A(t)= 1-√(1-4t) / 2tを一般化する代数列です。
生成関数が多項式係数を持つ特定の代数方程式を満たすと仮定します。 また、このようなシーケンスは非常に多くあります。カタロニア語の数には、このようなシーケンス、モツキンの数、および他の多くのものがあります。 しかし、これは最大のクラスではないことがわかりました。 より大きなクラス-二項和を学習します。 合計、多くの二項係数を取ります。 私は、ラティス上のすべてのベクトルを合計しますが、実際には、アルファとベータは線形関数です。 二項係数で関数が負になる場合、それは0であると見なされます。これらの数値が有限である場合にのみ興味深いです。 そして、そのようなケースはかなりあります。
この例は、まさにそのような場合を示しています。 私たちの前にいくつかの二項係数の合計があります。 ここで-0からn / 2まで、あなたは手放すことができます、もっとやる、二項係数だけが消え、ゼロになります。

その結果、多くの異なるシーケンス、二項和があります。 それらには、暴動の数、およびテーブルの座席配置の数が含まれます。 これはすべて、このような二項係数の観点から理解できます。 上にも下にも多くの階乗があります-すべてが理解できます。 これは大きなクラスですが、さらに大きなクラスであるP再帰シーケンスに興味があります。 これらは2つの方法で定義できます。 最も理解しやすい方法は、これらの数値に再帰的な関係がある場合、合理的な場合のように係数が定数ではなく、nに依存する多項式の場合です。 覚えているなら、ルーカスが発明したこの複雑であまり正確に記述されていない再帰関係は典型的なものです。 しかし、このような関係は他の多くのシーケンスにも存在します。

典型的な例はn!..定義上(n-1)です! * n。
別の例はカタロニア語番号です。 これは、2つの二項係数のある種の比率であることを覚えています。 結果は、nに依存する有理関数です。 したがって、それはゼロに等しくなければならない再帰関係として書くことができます。
これはあまり複雑な定理ではありません。 これは、生成関数が多項式係数を使用したこのような常微分方程式を満たすことを意味します。 シーケンスの仕組みを理解する別の方法を次に示します。 私たちにとって、P再帰シーケンスは最も重要なクラスになります。 以下の定理が含まれています。これらの定理は以下に記述されており、以前のすべてのクラスがこの中にあるという事実に基づいています。 最大級のクラスです。 代数列の場合、これは完全に明らかではなく、他の人にこれを証明するのは少し簡単です。
もちろん、このクラスにはすべての例が含まれているわけではありません。 素数はここに入らないと言う-それらには多項式の関係はない。 同様に、接続されたグラフの数には多項式の関係はありません。 それらは、ここでは当てはまらない、より複雑な例です。 パーティションの数がここに含まれていない場合、そのような例があるのは悪いことですが、定義上、P再帰シーケンスが多項式時間としてカウントされるのは素晴らしいことです。 ここに書かれていることは私たちにとって重要です。 シーケンスのクラスがあり、そのすべてをカウントできます。

それらを数え始める前に、特定の帰結を与えます。 このクラスでは、漸近性の観点からすればすべてがすでに良好であるという事実にあります。 P再帰シーケンスを使用している場合、漸近的な動作は既に非常に良好です。定数n!、ある程度、λn nα (log n) βがあります。 すべてがうまく機能しますが、残念ながら、この定理は証明されていません。 一部の人はそれを定理と考えていますが、彼女には特別な場合にのみ現れます。 しかし、原則として、このような特定のケースは重要です-指数以下に成長する非負のP再帰整数シーケンスがある場合、その動作は非常に単純です:λn nα (log n) β 。 彼女は、単純で良い漸近的な振る舞いをしています。 このクラスは非常に大きく、学習したいさまざまな組み合わせシーケンスが含まれています。 P再帰シーケンスは、私たちにとって最も重要なクラスです。

もう少し一般的なクラスがあり、それについてはほとんど知られていません。 生成関数が代数微分方程式を満たすシーケンスについて話しています。 この生成関数の特定の数の導関数を使用すると、それらは一緒になっていくつかの多項式を満たします。 これはより一般的なクラスです。 残念ながら、漸近的な振る舞いに関する結果はほとんどありません。 次に例を示します。 特定の数で始まり、その後、より少なく、より少なくなる順列を交互に取ってみましょう。 たとえば、長さ3-1、3、2、および2、3、1のこのような順列がちょうど2つあります。長さ4の順列が5つあります。
そのような順列の数については、かなり複雑な再帰関係があります。 これは、通常の微分ではなく、代数微分である方程式として書き直すことができます。2A '= A 2 +1。この形式では、解かれます。生成関数は、tan(t)+ sec(t)で明示的に記述できます。 , , , . , , , — n- . , .
, — , . , , , , . 150 , , , t n 2 , t n 3 , — 150 . , . , . , - . .
4. , . . . , .
— ?
— . , n .
— . , , ?
— . , , , , .
n! * t n , . , , defined, n! , . , .
— , , ?
— . , .
? . ?
— — ?
— , , , . , n — 2 n/2, — , . , — , . . — , . .
, , , . , , n, ? - , , labeled unlabeled. , . ? : e n — . , . , , . — .

. . . — -. «». , , , 0-1-, . , (5674123) (321) — .
, (4321), 4. (321) — . , , , .
, . , , . — , σ avoids ω.
. , - : «, ».
, . , , 0-1- . — , , . , . 簡単な例。 , — (12). 7, ? . , (12), , . : (7654321).
, . .

. , (123), 3. , : , , . , 1915 — . 3, , . , (213), . , , , 3: . . 4, 4, 4 — . .
, , . . , . , , , , , .
, , . . , 2, — , , , . , . , . , , , (1342). , , .
— , , . , - , , .

, , : , , , -, .
, , . . , , , , . 31 80 , .
31 — . - , , . , . ? ナンセンス。 , 80 . .

, , - , , . , , — . 90- , . , , : — 1990 . - , , , . , 4, (1324), , , -. .
31 , 4. , , , . - - . -, . -, ? .

? . , F F', , 2, , . : . .
2. , , F F'. , ? , , , . , ?
, . , — F F' «» «». - .
, , , . — , . , .

, k , . , . , , - . — , . , .
, . , , , . . — . , -. , - .
, , , . 2.

, = NP. : , , .
NP? , , NP. , , .
⊕P. , . . , = ⊕P = NP — . , ⊕P — , . , . , , — . . — .
, . , n- . imput size n log (n) bits, n log (n) . , n, input. , P ≠ ⊕P EXP ≠ ⊕EXP. , input unary, not in binary. Computation Complexity.

, . EXP ≠ ⊕EXP, — 31 — , , , , n. , , defined, AD, 1 , — Computation Complexity. , . - , - — .
, , , , n — , .
1982 : - , ? ? - 31 80 — , . , , Computation Complexity , , , .

, . , , - . , 1. . — - . — 0, — 1 . , , . . , , .
- . , r 0 (n)a n + r 1 (n)a n-1 . . , , .

. . 0, 1, 0,0, 0,1, 1,0 1,1, 0,0,0, 0,0,1 0,1,0, .

. : , . , . , 80 80, .
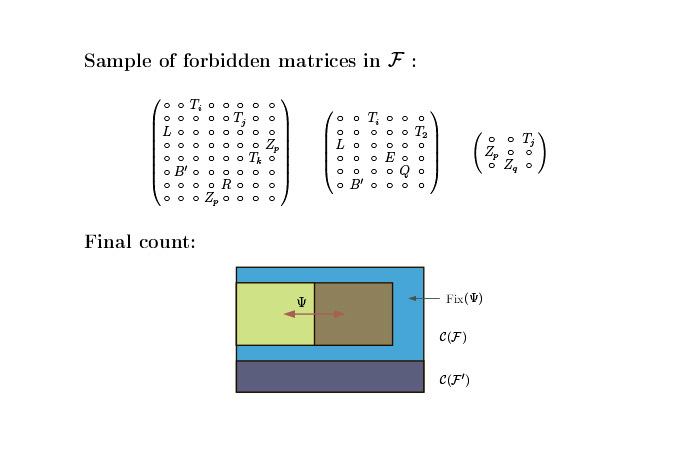
, 88. , - , 1010, . , , :

, , — , , . , , . , , , , , .

— . . 88 1010. , … 1 ? . , , -, , , — , . , . , , , 2 n . , 1 + ε n - ε, , - . .

. . , -, ADE. , . . , , , K! + K n.
. , n 2 . , , — . ! + , , , , . , .

? ? , . , , Wang tiles. 11. , . Wang tiles, . : , , ? , , .
, , . . , , . . - , , .
.


. : , 1. , , ? , , , . , , , 2, . , , -? , .
, , , . , . , , — . 31 . , , .
ただし、Seilbergerは正しいと考えられ、そのような順列を含まない順列のシーケンスはP再帰的ではありません。
最後の仮説は、パターンを含まない数値をカウントするタスクは、その計算クラスでは難しいことを示唆しています。単純に定式化する場合でも、少し時間がかかります。
実際には、それだけです。 どうもありがとう。