How I created a filter that does not corrupt the image even after a million runs - part 2

In the first part of this post, I talked about how repeated use of standard halfpel filters creates distorted images, and then showed a new filter that does not have this problem.



It was a little more blurry and this would not suit everyone. However, it was better than its alternatives - in fact, this filter was used in the original version of Bink 2 . Due to the constant workload, I never managed to return to him again and examine him in more detail.



But now that I have found the time to return to this filter and write an article about it, I should finally ask the question: is there a less blurring filter that still retains the property of “infinite stability”?



Spoiler warning: the correct answer is “probably not” and “definitely there.” But before we get to why there are two answers to this question and what they mean, let's better prepare the test bench.

Offset adjustment

When I initially worked on this problem, I had no idea what I was looking for. I did not even know that there was such a thing as an “infinitely stable” halfpel filter, so I did not create a system in its search. I was just looking for something that would withstand the “many” filter iterations without image distortion. All images from the first part reflect this methodology: the image is shifted from right to left half a pixel at a time, that is, if you apply the filter 100 times, the resulting image will be shifted by 50 pixels.



Now that we know what we are actually looking for , we can be a little more precise. Applying the halfpel filter twice, we shift the image exactly one pixel. That is, if we just move the image one pixel back , it will remain in the same space. Thanks to this, the test will look much more beautiful, because we will not only be able to apply the filter any number of times, without fear that the image will "crawl away" from the screen, but we will also be able to find the difference of the image with previous versions and with the original.



This will allow us to test the filters automatically. We simply apply the filter many times and see one of two things: either convergence to an unchanged image, indicating that the filter is infinitely stable, or a significantly large deviation from the original image, indicating that the filter is “broken”. For these tests, I chose the average error per channel 64 (out of 255), or the maximum error for any of the channels to the full 255 as “significantly large”. If any of these conditions is true, we will assume that the filter “broke” ".

Re-testing the filters from the first part

So, now we better understand how to test these filters, so let's take a fresh look at the filters from the first part. Let's start with a bilinear, which, of course, is not very interesting:









This is a picture after 244 iterations. As you might expect, the image gradually “breaks” due to the constant averaging of pixels. But even it gradually reaches the limit of the average error.



Here is h.264:









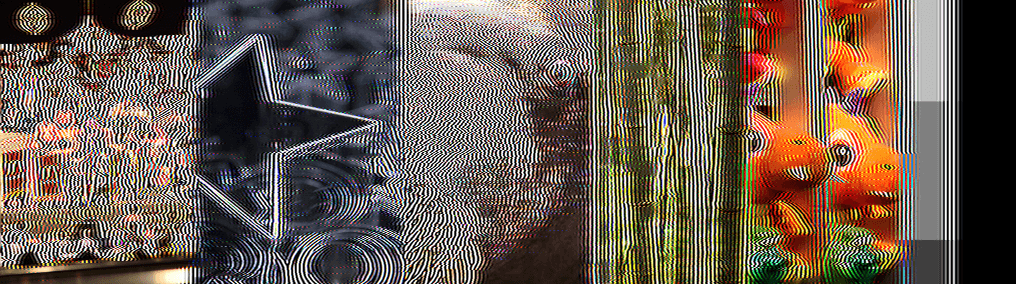
To break the image, 78 iterations are enough for him. The HEVC filter with 8 samples behaves a little better, but still breaks after 150 iterations:









Lanczos with 6 samples breaks after 166 iterations:









That's all our broken filters. All that remains is my integer filter:









As expected, he was not the only one to break. It converges to an infinitely stable image after 208 iterations.



What we know is quite remarkable here: at least for a wide range of test images this filter is infinitely stable , that is, it will never create an artifact, no matter how many times it is used.



This brings us back to the original question: is he really the best? And you already know the answers, because at the beginning of the article I also wrote: “probably not” and “definitely, yes”.



Let's first look at the “probably not” part first.

Integer filters

So, in the first part of the post, I mentioned that the filter core I found was the “best found”, and this is its peculiarity. And here is the feature:



When I was looking for this filter, in fact I was not looking for the best filter. I was looking for the best filter that can be expressed with a very small number of integer shifts, additions and subtractions . It may seem strange, but take your time.



You may have noticed that when I showed the coefficients of h.264, HEVC and the bilinear filter, as well as my filter, I wrote them down as integer numerators over integer denominators, like this:

MyKernel[] = {1.0/32.0, -4.0/32.0, 19.0/32.0, 19.0/32.0, -4.0/32.0, 1.0/32.0};
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

But in the case of windowed sinc, I acted differently and wrote it like this:

 LanczosKernel[] = {0.02446, -0.13587, 0.61141, 0.61141, -0.13587, 0.02446};
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

The reason for this is that windowed sinc is actually inferred from a continuous mathematical function that has nothing to do with ordinary integer fractions. When using this filter, floating point numbers (as accurately as possible) are used that correspond to the values ​​of the sinc function. If you strive to apply them accurately, then you should not round them to ordinary fractions, because this will add an error.



Video codecs traditionally cannot afford to perform such operations. Floating-point operations on such “heavy” tasks as motion compensation are simply impossible to use on low-power or specialized equipment. This is especially true if we are talking about industry-standard codecs that should run on a wide range of devices, including low-cost, low-cost embedded chips.



Moreover, even if you execute them on the CPU, modern instruction sets are based on SIMD, that is, integer operations on the CPU can still be performed faster: you can fit two 16-bit integers into the space of one 32-bit float, essentially doubling the performance of operations, therefore, if we consider the exact number of cycles per operation, then a floating point is not always the fastest option.



Now you see why this feature was important. Since I needed only simple 16-bit integer operations, I looked for those kernels that can be expressed as small integers over divisors in the power of two to 64 and no more. This is a much more limited set of filters compared to if I were considering any set of 6 floating point coefficients.



Similarly, for reasons of efficiency, I did not consider any other number of samples. The only option was 6 or less, so I did not even test versions with 8 or 10 samples.



Thus we came to the first answer: "probably not." If we adhere to these restrictions, then most likely we will not find a better filter that can be applied an infinite number of times without degradation. The filter core from the first part is probably the best we can find, although it must be admitted that I cannot prove it exhaustively.



But what if we do not need to adhere to such restrictions?

Floating point version

If we get rid of the restrictions specific to the original version of Bink 2 (which is now quite outdated - a lot of revisions have since been released) and use arbitrary floating-point coefficients, then how much can the results be improved?



Well, since we know that my integer kernel never degrades, and we know that Lanczos is sharper, but degrades, it is logical that we can find a place between two sets of coefficients where degradation begins. So I wrote a program that helped me find this particular point, and here is what kernel I found:

 MyFloatKernel6[] = {0.027617, -0.130815, 0.603198, 0.603198, -0.130815, 0.027617};
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

This kernel requires 272 iterations to converge, but it is infinitely stable and looks much sharper than my integer filter:









In fact, it is almost indistinguishable from the original:









Almost ... but not quite. If you look closely, you can still see blurring and attenuation in high-contrast areas. The easiest way to see this is in the eye of an orange "dinosaur" and in bright light areas behind bamboo.



That is, a 6-sample floating point filter is definitely better, but it's not perfect. Can it be improved yet?

Increase filter width

Initially, a filter with 6 samples was selected for the same reasons as fractions with small integers: I was looking for an extremely efficient filter. But now we are doing research and have already moved on to floating point numbers, so why not consider a wider filter?



Combining our 6-sample integer filter with the 6-sample Lanczos, we got a very good filter. Why don't we pair it with the 8-sample Lanczos?



The 8-sample Lanczos looks like this:

 Lanczos8[] = {-0.01263, 0.05976, -0.16601, 0.61888, 0.61888, -0.16601, 0.05976, -0.01263};
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Like the 6-sample Lanczos, it is very unstable and collapses after 178 iterations:









If we look for a better filter between a 6-sample integer filter and an 8-sample Lanczos, we will find this rather remarkable 8-sample filter:

 MyFloatKernel8[] = {-0.010547, 0.052344, -0.156641, 0.614844, 0.614844, -0.156641, 0.052344, -0.010547};
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

As an infinitely stable filter, it performs amazingly well. It converges after 202 iterations (convergence is faster than my two filters), and it resembles the original so much that it is difficult to make out which of them is which:









Here is the original for reference again:









Compared to my original integer filter, there is a significant improvement.

How do infinitely stable filters work?

I was going to end this post something like this:



“I don’t know exactly how it all works. In other areas where I have worked with the infinitely applicable transformations, I know how boundary mathematics is performed and useful analysis is created. First of all, it comes to the analysis of the boundary surface for subdivision surfaces, where the eigenvalues ​​and eigenvectors of the subdivision matrix are calculated, after which it is possible to precisely take the limit to an infinite degree. But I have no experience in performing such an analysis for halfpel filters, because they do not leave pixels in place, but shift them sideways. "



That was my plan. But between the writing of the first and second parts, I mailed the results of the improved filter to Fabien Giessen and Charles Bloom . It is not surprising that they knew the mathematics necessary for the analytical study of this problem. It turned out that for filters there really is an analysis of eigenvalues ​​and vectors, but it does not quite work out that way.



But it can be easily done - in fact, it is built into CAM programs as a trivial one-step process and we can really look at the eigenvalues ​​for filters. He does not give us complete answers, because here the fact of rounding (or truncation) to 8 bits (or 10 bits, or 12 bits) after each filtering is important, because truncation affects the method of accumulating errors in comparison with infinitely accurate algebra.



Unfortunately, since this is not at all my area of ​​expertise, I cannot even get a close overview of this analysis. I asked Fabien and Charles if they could write posts with the good information that they sent me in the mail (they both have technical blogs - the ryg blog and cbloom rants ), and Fabien wrote an excellent series of articles on the mathematical foundations of stable filters . If you are interested in the theoretical structure of what is happening in my two posts, then I recommend reading this series!