Two pages were enough to prove the 30-year hypothesis from the field of computer science.

The “sensitivity” hypothesis baffled many prominent computer scientists, but its new evidence turned out to be so simple that one researcher could reduce it to a single tweet

The work published this summer puts an end to the nearly 30-year history of the hypothesis regarding the structure of the fundamental building blocks of computer circuits. This hypothesis of “sensitivity” has perplexed many prominent computer scientists for years, but its new proof turned out to be so simple that one researcher could reduce it to a single tweet.



“This hypothesis was one of the most annoying and shameful open problems in all combinatorics and theoretical computer science,” wrote Scott Aaronson of the University of Texas at Austin in his blog. “The list of people who tried to prove it and failed to do it is a list of the most prominent people in discrete mathematics and theoretical computer science,” he added in an email.



This hypothesis is associated with Boolean functions - the rules for converting strings of incoming bits (zeros and ones) into a single bit. One such rule produces 1 when all incoming bits are 1, and 0 otherwise; another rule returns 0 if the line contains an even number of units, and 1 otherwise. Each computer circuit is a combination of Boolean functions, which makes them "the building material of everything that is done in computer science," said Rocco Cenedio of Columbia University.





Over the years, many ways have been developed in computer science to measure the complexity of a given Boolean function. Each measure uses its own aspect of how the input line information determines the output bit. For example, the “sensitivity” of a Boolean function, roughly speaking, indicates the probability that changing a single bit at the input will change the bit at the output. And the “request complexity” calculates how many incoming bits need to be requested in order to know with certainty what the outgoing will be.



Each measure gives its own unique point of view on the structure of a Boolean function. However, computer scientists found that almost all of these measures fit into a universal platform, and that by the value of one of them one can approximately judge the significance of the others. And only one measure of complexity did not fit into this scheme: sensitivity.



In 1992, Noam Nisan of the Hebrew University of Jerusalem and Mario Szeged, now working at Rutgers University, suggested that sensitivity still fits into this platform. But no one could prove it. “This question, I would say, was outstanding in the field of studying Boolean functions,” said Cenedio.



“People wrote long, complex works, trying to make very little progress,” said Ryan O'Donnell of Carnegie Mellon University.



And now, Hao Huang , a mathematician from Emory University, has proved the sensitivity hypothesis with the help of a brilliant but elementary two-page proof related to the combinatorics of points on cubes. “It's beautiful, like a precious pearl,” wrote Claire Matthew, of the French State Center for Scientific Research in an interview on Skype.



Aaronson and O'Donnell called the work of Juan "book" proof of the hypothesis of sensitivity, referring to the concept of the "heavenly book" by Pal Erdös, in which God writes down ideal proofs of each theorem. “It’s hard for me to imagine that even God knows a simpler proof of the sensitivity theorem,” wrote Aaronson.

Sensitive topic

Imagine, said Matthew, that you are filling out a questionnaire on the bank loan application form with answers that may be yes / no. When you are done, the banker will evaluate the results and tell you if you are suitable for a loan. This process is a Boolean function: your answers are incoming bits, and the banker's decision is outgoing.



If your application is denied, you can think about whether you could change the result by lying in one single question - perhaps by stating that you earn more than $ 50,000 a year, although this is not so. If this lie changes the result of consideration, computer scientists will call such a Boolean function “sensitive” to the value of a particular bit. If, for example, you could lie in one of seven places, and each time change the result, then the sensitivity of the Boolean function of evaluating your loan application is seven.



Computer scientists define the overall sensitivity of the Boolean function as the highest sensitivity value for all possible options for filling out an application. In a sense, this measure calculates how many issues will be really important in most borderline cases - in applications, the result of which is most easily changed if the applications themselves are slightly modified.





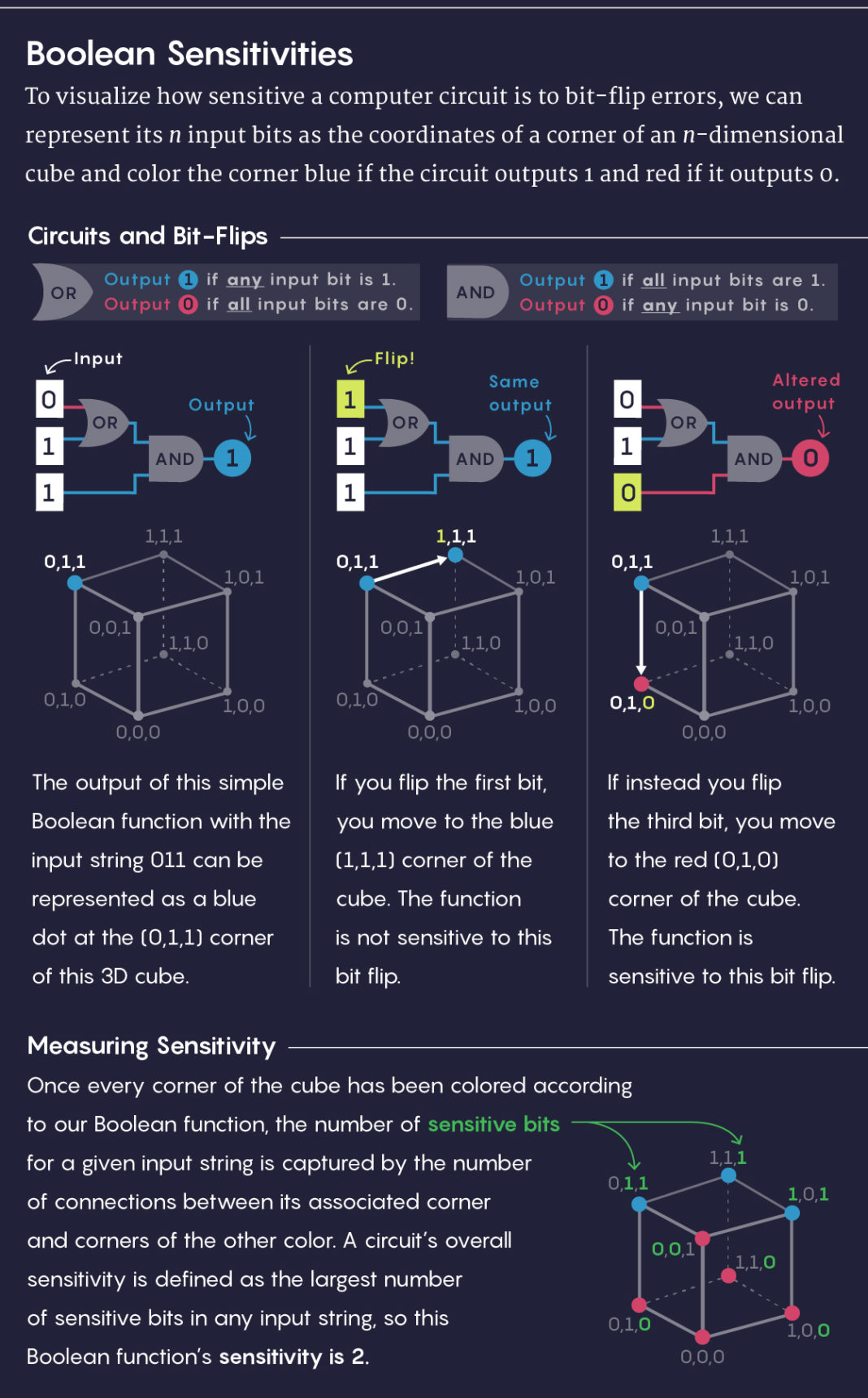
To visualize the sensitivity of the circuit to errors with the reversal of the bits, n incoming bits can be represented as the coordinates of the vertices of an n-dimensional cube. We will color the vertex blue if the path produces 1, and red if 0.



In the middle left: the output of a simple Boolean function with input 011 can be represented by a blue dot on the top of the cube (0,1,1).

Center: Turning the first bit, we will go to the blue top of the cube (1,1,1). The function is not sensitive to the inversion of this bit.

In the middle right: Turning the third bit, we go to the red top of the cube (0,1,0). The function is sensitive to the reversal of this bit.



Having colored all the vertices of the cube, we get the number of sensitive bits for a given incoming line equal to the number of connections between the corresponding vertex and the vertices of a different color. The loop sensitivity is defined as the largest number of sensitive bits in any input line, so this function has a sensitivity of 2.



Sensitivity is usually one of the easiest measures to calculate complexity, but it is not at all a simple explanatory measure. For example, our banker, instead of giving you a form to fill out, could start with a single question, and then use your answer to determine which question to ask next. The largest number of questions that a banker will need to ask before arriving at a solution is the complexity of requesting a Boolean function.



Such a measure appears in a variety of situations - for example, a doctor may want to send the patient to collect as few tests as possible in order to make a diagnosis, or a machine learning expert may want to create an algorithm that studies as few properties of the object as possible before he will be able to correctly classify it. “In many situations — diagnostic or training — you like the basic rule to have low query complexity,” O'Donnell said.



Among other measures is the search for the simplest way to write a Boolean function in the form of a mathematical expression, or to calculate how many answers the banker will have to show to the boss in order to prove that the application has been processed correctly. There is even a variant of the complexity of the query from quantum physics, when the banker asks a “superposition” of several questions at once. Understanding how this measure is related to other complexity measures, researchers better understand the limitations of quantum algorithms.



Computer scientists have proven that there is a close relationship between all of these measures, with the exception of sensitivity. More specifically, they found that they are related to each other by polynomial dependence - for example, one measure can be expressed as a square or cube of another. And only sensitivity stubbornly resisted, not wanting to integrate into this convenient classification scheme. Many researchers suspected that it should be suitable for it, but could not prove that there are no strange Boolean functions whose sensitivity is connected with other measures not by polynomial but by exponential dependence, which in this case would mean that the sensitivity measure is fundamentally smaller than the rest.



“This question has kept people awake for 30 years,” Aaronson said.

Corner the solution

Juan found out about this hypothesis at the end of 2012, having lunch with mathematician Michael Sachs of the Institute for Advanced Studies, where Juan was a postdoc. He was immediately fascinated by the simplicity and elegance of the hypothesis. “And from that moment I became obsessed with thoughts about her,” he said.



Juan added the sensitivity hypothesis to the “secret list” of problems he was interested in, and when he found out about some new mathematical tool, he wondered if he could help him. “Each time after the publication of another work, I returned to this task,” he said. “Of course, I allocated time and energy to work on more realistic tasks.”





Hao Huang on a recent vacation in Lisbon



Juan, like many in the research community, knew that the sensitivity hypothesis could be proved if mathematicians succeeded in proving another hypothesis with a simpler condition concerning a set of points on cubes of different dimensions. There is a natural way to go from a string of zeros and ones to a point on an n-dimensional cube: just use n bits as the coordinates of that point.



For example, four two-bit lines - 00, 01, 10 and 11 - correspond to the four corners of a square on a two-dimensional plane: (0,0), (0,1), (1,0) and (1,1). Similarly, eight three-bit lines correspond to eight corners of a three-dimensional cube, and so on, for higher dimensions. The Boolean function can be considered the rule of coloring these cube angles with two different colors (for example, red for 0 and blue for 1).



In 1992, Craig Gotsman , now working at the New Jersey Institute of Technology and Nati Lignal from Hebrew University, realized that the proof of the sensitivity hypothesis can be reduced to the answer to a simple question about cubes of different dimensions: if you take any set consisting of more than half the vertices of cubes , and color them red, is there a red dot necessarily connected to many other red dots (by “connected” dots we mean that two vertices are connected by a common edge, and not located diagonally).



If our subset contains exactly half the vertices of the cube, they may not be connected to each other. For example, among the eight corners of a three-dimensional cube there are four points,

(0,0,0), (1,1,0), (1,0,1) and (0,1,1) are located diagonally from each other. But as soon as more than half of the vertices of a cube of any dimension turn red, among them red points must be connected among themselves. The question is how are these connections distributed? Will there be at least one of these peaks with a large number of connections?



In 2013, Juan began to think that the best way to understand this issue would probably be to use the standard method of representing the network using a matrix that keeps track of which points are connected and then studies a set of numbers called eigenvalues ​​of the matrix. For five years, he periodically returned to this idea, but to no avail. “At least because of the fact that I thought about her before going to bed, it was easier for me to sleep for many nights,” he commented on Aaronson’s blog entry.



Then in 2018, Juan thought about using the Cauchy alternation theorem, a mathematical statement of 200 years ago, connecting the eigenvalues ​​of a matrix with a submatrix, which perhaps makes it an ideal tool for studying the relationship between a cube and a subset of its vertices. Juan decided to request a grant from the State Science Foundation to further explore this idea.



Then, last month, sitting in a hotel in Madrid and filling out a grant application, he suddenly realized that he could extend the use of this approach to the very end, simply changing the signs of some numbers from the matrix. In this way, he was able to prove that in any set of more than half the vertices of an n-dimensional cube there will exist a point associated with at least √n other points - and the sensitivity hypothesis immediately follows from this result.



When Matthew received Juan’s work in the mail, her first reaction was “oops,” she said. “When a task has existed for 30 years and everyone knows about it, then its proof must be either very long and complex, or very deep.” She opened the file with the work, expecting that she won’t understand anything.



However, the proof was simple enough for Matthew and other researchers to digest it in one sitting. “I think that this fall, students will tell him as part of one lecture in each master's course in combinatorics,” she wrote on Skype.



Juan’s result turned out to be even stronger than necessary to prove this hypothesis, and this force should give us new ideas about measures of complexity. “It has been added to our toolkit and may help answer other questions related to Boolean functions,” said Cenedio.



But most importantly, the result of Juan allows us to stop all worries about whether sensitivity is some strange alien in the world of measures of complexity, said Cenedio. “I think that in the evening, learning about these results, very many were able to sleep peacefully.”