おそらく、一般的に検索を行うサービスであれば、遅かれ早かれ、ユーザークエリのエラーを修正する方法を学ぶ必要が生じます。 人間のエラー ユーザーは常に封印され、誤解され、検索の品質は必然的にこれに苦しみます-そして、ユーザーエクスペリエンスに影響します。



さらに、各サービスには固有の固有の用語があり、ボキャブラリーはタイプミス修正プログラムを操作できるはずであり、既存のソリューションの使用を非常に複雑にします。 たとえば、このようなリクエストは、保護者の編集を学習する必要がありました。







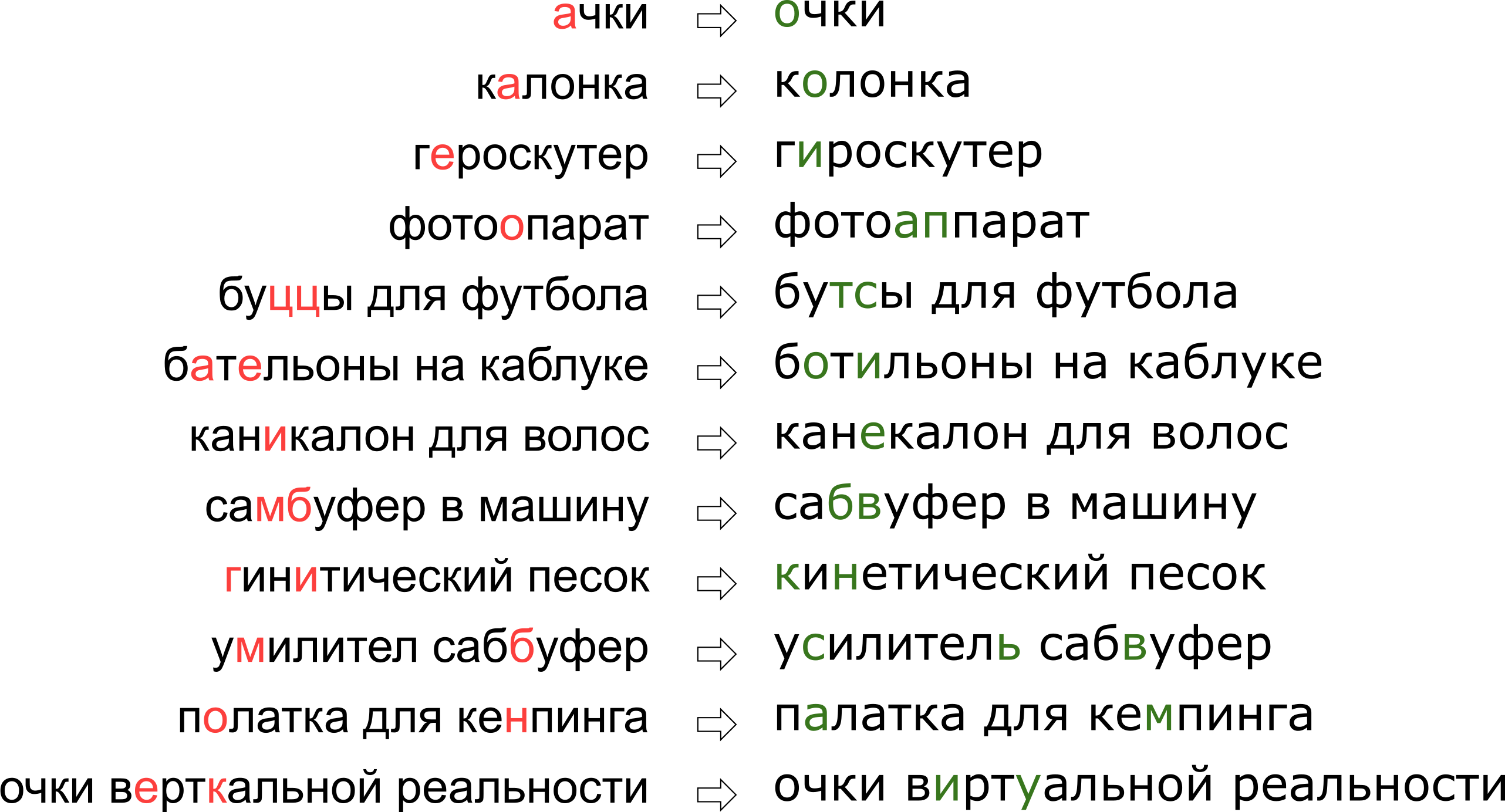
ユーザーに彼の垂直現実の夢を否定したように思えるかもしれませんが、実際には、文字Kは文字Uの隣のキーボード上に単純に立っています。



この記事では、モデルの作成からPythonおよびGoでのコードの作成まで、タイプミスを修正するための古典的なアプローチの1つを分析します。 ボーナスとして-私のレポート「 Vertical Vertices」のビデオ： Highload ++ での検索クエリのタイプミスの修正 。

問題の声明

そのため、封印されたリクエストを受け取り、それを修正する必要があります。 通常、問題は次のように数学的に提起されます。

• 与えられた言葉 $$$s$ エラーとともに送信された;
• 辞書を持っている $$$\シグマ$ 正しい言葉;
• 辞書内のすべての単語wには条件付き確率があります $$$P（w | s）$ 言葉の意味 $$$w$ 言葉を受け取ったなら $$$s$ ;
• 辞書から単語wを最大の確率で見つける必要があります $$$P（w | s）$ 。

このステートメント-最も基本的なもの-は、複数の単語のリクエストを受け取った場合、各単語を個別に修正することを示唆しています。 もちろん、実際には、隣接する単語の互換性を考慮して、フレーズ全体を修正する必要があります。 これについては、「フレーズを修正する方法」セクションで説明します。



2つの不明確な瞬間があります-辞書の入手場所とカウント方法 $$$P（w | s）$ 。 最初の質問は簡単と見なされます。 1990 [1]辞書は、 スペルユーティリティデータベースと電子的に利用可能な辞書から編集されました。 2009年にGoogle [4]を使用すると、インターネット上で最も人気のある単語（および人気のあるつづりの間違い）を簡単に理解できるようになりました。 私はこのアプローチで保護者を作りました。



2番目の質問はより複雑です。 彼の決定が通常ベイズの公式の適用から始まるという理由だけで！

$$

$$P（w | s）= \ mathrm {const} \ cdot P（s | w）\ cdot P（w）$$

ここで、元の不可解な確率の代わりに、2つの新しい、少し理解しやすいものを評価する必要があります。 $$$P（s | w）$ -単語を入力するときの確率 $$$w$ 封印して得ることができます $$$s$ 、そして $$$P（w）$ -原則として、ユーザーが単語を使用する確率 $$$w$ 。



評価する方法 $$$P（s | w）$ ？ 明らかに、ユーザーはbをSと比べてAとOを混同する可能性が高いです。 また、スキャンしたドキュメントから認識されたテキストを修正すると、rnとmの間で混乱する可能性が高くなります。 何らかの方法で、エラーとその確率を記述する何らかの種類のモデルが必要です。



このようなモデルは、ノイズの多いチャネルモデル（ノイズの多いチャネルモデルです。この場合、ノイズの多いチャネルは、ユーザーのブロックの中心から始まり、キーボードの反対側で終わります）、または簡単に言えば、エラーモデルがエラーモデルです。 以下の別のセクションで説明するこのモデルは、スペルミスと実際のタイプミスの両方を考慮する必要があります。



単語を使用する確率を評価- $$$P（w）$ -それはさまざまな方法で可能です。 最も単純なオプションは、テキストのいくつかの大きなコーパスで単語が出現する頻度を取ることです。 もちろん、保護者にとっては、フレーズのコンテキストを考慮して、より複雑なものが必要です-別のモデル。 このモデルは、言語モデル、言語モデルと呼ばれます。

エラーモデル

最初のエラーモデルが考慮されました $$$P（s | w）$ 、トレーニングセットの基本的な置換の確率を計算します。Eの代わりに何回書いたのか、Tの代わりに何回Tを書いたのか、T-Tの代わりに何回書いたのかなど[1]。 その結果、いくつかのローカル効果を学習できる少数のパラメーターを持つモデルが作成されました（たとえば、EとIを混同することがよくあります）。



私たちの研究では、2000年にBrillとMooreによって提案され[2]、後で再利用された（たとえばGoogleの専門家[4]によって）より発展したエラーモデルに落ち着きました。 ユーザーが別々の文字で考えないことを想像してください（EとIを混同し、Yの代わりにKを押し、ソフト記号をスキップします）。たとえば、TSYAをTYSYAに、YをKに、SHAをSHCHYAに、SSに置き換えますCなどに。 ユーザーが封印され、TSYAの代わりにTHYと記述されている確率は、 $$$P（\ text {thousand} \ rightarrow \ text {thousand}）$ モデルのパラメーターです。 すべての可能なフラグメントについて $$$\ alpha、\ beta$ 私たちは数えることができます $$$P（\アルファ\右矢印\ベータ）$ 、その後、所望の確率 $$$P（s | w）$ ブリルアンドムーアモデルで単語wを入力しようとするときの単語sのセットは、次のようにして取得できます。 各パーティションについて、すべてのフラグメントwの確率の積を計算して、対応するフラグメントsにします。 このようなすべてのパーティションの最大値は、の値として取得されます $$$P（s | w）$ ：

$$

$$P（s | w）= \ max_ {s = \ alpha_1 \ alpha_2 \ ldots \ alpha_k、w = \ beta_1 \ beta_2 \ ldots \ beta_k} P（\ alpha_1 \ rightarrow \ beta_1）\ cdot P（\ alpha_2 \ rightarrow \ beta_2）\ cdot \ ldots \ cdot P（\ alpha_k \ rightarrow \ beta_k）\ ,.$$

「アクセサリ」ではなく「アクセサリ」を印刷する確率を計算するときに発生するパーティションの例を見てみましょう。

$$

$$\ begin {matrix} \ text {ak}＆\ text {cec}＆\ text {sou}＆\ text {a}＆\ text {p} \\ \ downarrow＆\ downarrow＆\ downarrow＆\ downarrow＆\下矢印\\ \ text {a}＆\ text {cc}＆\ text {e}＆\ text {soua}＆\ text {p} \ end {matrix}$$

お気づきかもしれませんが、これはあまり成功していないパーティションの例です。単語の一部が互いに可能な限りうまく重なり合っていないことは明らかです。 数量 $$$P（\テキスト{ak} \右矢印\テキスト{a}）$ そして $$$P（\テキスト{p} \右矢印\テキスト{p}）$ まだそんなに悪くない $$$P（\テキスト{sou} \右矢印\テキスト{e}）$ そして $$$P（\テキスト{a} \右矢印\テキスト{soua}）$ ほとんどの場合、このパーティションの最終的な「スコア」は完全に悲しくなります。 より成功したパーティションは次のようになります。

$$

$$\ begin {matrix} \ text {ak}＆\ text {ce}＆\ text {ss}＆\ text {y}＆\ text {ar} \\ \ downarrow＆\ downarrow＆\ downarrow＆\ downarrow＆\下矢印\\ \ text {ak}＆\ text {ce}＆\ text {c}＆\ text {y}＆\ text {ar} \ end {matrix}$$

ここでは、すべてがすぐに所定の位置に落ち、最終的な確率は主に値によって決定されることは明らかです $$$P（\テキスト{ss} \右矢印\テキスト{s}）$ 。

計算方法 $$$P（s | w）$

2つの単語に対して可能なパーティションの順序があるという事実にもかかわらず $$$O（2 ^ {| s | + | w |}）$ 動的計画法計算アルゴリズムの使用 $$$P（s | w）$ かなり速くすることができます-のために $$$O（| s | ^ 2 | w | ^ 2）$ 。 アルゴリズム自体は、 レーベンシュタイン距離を計算するためのワーグナー・フィッシャーアルゴリズムに非常に似ています。



行が正しい単語の文字に対応し、列が封印されたものに対応する長方形のテーブルを作成します。 アルゴリズムの終わりまでに行iと列jの交点にあるセルは、 w[:i]



を印刷しようとすると、正確にs[:j]



を取得する可能性があります。 それを計算するには、前の行と列のすべてのセルの値を計算し、対応する値を掛けてそれらを調べるだけで十分です $$$P（\アルファ\右矢印\ベータ）$ 。 たとえば、テーブルが埋められている場合









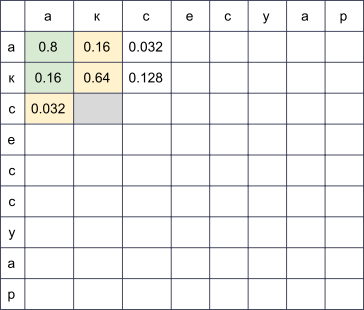
、4番目の行と3番目の列（灰色）のセルを塗りつぶすには、最大値を取得する必要があります $$$0.8 \ cdot P（\テキスト{cc} \右矢印\テキスト{c}）$ そして $$$0.16 \ cdot P（\テキスト{c} \右矢印\テキスト{k}）$ 。 同時に、写真の緑色で強調表示されているすべてのセルを実行しました。 フォームの変更も考慮する場合 $$$P（\ alpha \ rightarrow \ text {空行}）$ そして $$$P（\テキスト{空の行} \右矢印\ベータ）$ 、黄色で強調表示されているセルを移動する必要があります。



上で述べたように、このアルゴリズムの複雑さは $$$O（| s | ^ 2 | w | ^ 2）$ ：テーブルに記入します $$$| s | \回| w |$ 、必要なセル（i、j）を埋める $$$O（i \ cdot j）$ 操作。 ただし、一部の制限された長さ以下のフラグメントにのみ考慮を制限する場合 $$$L$ （たとえば、[4]のように2文字以下）、複雑さは次のように減少します。 $$$O（| s | \ cdot | w | \ cdot L ^ 2）$ 。 私の実験でロシア語のために $$$L = 3$ 。

最大化する方法 $$$P（s | w）$

私たちは見つけることを学びました $$$P（s | w）$ 多項式時間は良いです。 しかし、辞書全体で最適な単語をすばやく見つける方法を学ぶ必要があります。 そして最高は $$$P（s | w）$ 、そして $$$P（w | s）$ ！ 実際、次のような妥当な上位（たとえば、ベスト20）の単語を取得すれば十分です。 $$$P（s | w）$ 、それを言語モデルに送信して、最も適切な修正を選択します（詳細は以下を参照）。



辞書全体をすばやく調べる方法を学習するために、上記の表には、共通の接頭辞を持つ2つの単語について多くの共通点があることに注意してください。 確かに、「アクセサリ」という単語を修正するときに、「アクセサリ」と「アクセサリ」という2つの語彙の単語を記入しようとすると、最初の9行がまったく変わらないことに気付くでしょう。 次の2つの単語の共通プレフィックスが十分に長くなるように辞書パスを配置できれば、多くの計算を節約できます。



そして、できる。 語彙を取り上げてトライしてみましょう。 深さを見ていくと、目的のプロパティが得られます。ほとんどのステップは、テーブルから最後の数行を埋める必要があるときに、ノードからその子孫までのステップです。



このアルゴリズムは、いくつかの追加の最適化により、100ミリ秒以内に典型的なヨーロッパ言語の辞書を50〜10万語でソートすることができます[2]。 また、結果をキャッシュすると、プロセスがさらに高速になります。

取得方法 $$$P（\アルファ\右矢印\ベータ）$

計算 $$$P（\アルファ\右矢印\ベータ）$ 検討中のすべてのフラグメント-エラーモデルを構築する上で最も興味深く重要な部分。 これらの量から品質が決まります。



[2、4]で使用されているアプローチは比較的単純です。 たくさんのカップルを見つけましょう $$$（s_i、w_i）$ どこで $$$w_i$ 辞書からの正しい単語であり、 $$$s_i$ -その密封されたバージョン。 （正確に見つける方法は少し低いです。）次に、これらのペアから特定のタイプミスの可能性を抽出する必要があります（あるフラグメントを別のフラグメントに置き換える）。



各ペアについて、そのコンポーネントを取得します $$$w$ そして $$$s$ そして、文字間の対応を構築し、レーベンシュタイン距離を最小化します。

$$

$$\ begin {matrix} \ text {}＆\ text {}＆\ text {}＆\ text {}＆\ text {}＆\ text {}＆\ text {}＆\ text {a}＆\ text {p} \\ \ text {a}＆\ text {k}＆\ text {c}＆\ text {e}＆\ text {c}＆\ text {}＆\ text {y }＆\ text {a}＆\ text {p} \ end {matrix}$$

これで、置換がすぐに表示されます。a→a、e→、c→c、c→空の文字列などです。 また、2つ以上の文字の置換も確認します。ak→ak、ce→si、ec→is、ss→s、ses→sis、ess→isおよびその他など。 これらすべての置換は、コーパスに単語sが出現するたびにカウントする必要があります（コーパスから単語を取得した場合、これは非常に可能性が高い）。



すべてのペアを渡した後 $$$（s_i、w_i）$ 確率のために $$$P（\アルファ\右矢印\ベータ）$ ペアで発生した置換の数α→βが受け入れられ（対応する単語の発生を考慮して）、フラグメントαの繰り返し数で除算されます。



カップルを見つける方法 $$$（s_i、w_i）$ ？ [4]では、そのようなアプローチが提案されています。 大量のユーザー生成コンテンツ（UGC）を取得します。 Googleの場合、それは何億ものWebページのテキストでした。 私たちには何百万ものユーザー検索とレビューがあります。 通常、コーパス内でエラーのあるバリアントよりも正しい単語が頻繁に見つかると想定されています。 それで、コーパスのレーベンシュタインによると、それに近い各単語の単語を見つけましょう。 人気を取る $$$w$ 、あまり人気がない-のために $$$s$ 。 そのため、ノイズが多くなりますが、トレーニング対象のペアは非常に多くなります。



このペアマッチングアルゴリズムには、改善の余地が多くあります。 [4]では、発生によるフィルターのみ（ $$$w$ 人気の10倍 $$$s$ ）、ただし、この記事の著者は、言語の先験的な知識を使用せずにゴシップを作成しようとしています。 ロシア語のみを考慮する場合、たとえば、 ロシア語の単語形式の辞書のセットを取得し、単語とのペアのみを残すことができます $$$w$ 辞書にある（辞書にはサービスに固有の語彙が含まれていない可能性が高いため、お勧めできません）、または逆に、辞書にある単語sとのペアを破棄します（つまり、封印されないことがほぼ保証されます）。



受信したペアの品質を改善するために、ユーザーが2つの単語を同義語として使用するかどうかを決定する簡単な関数を作成しました。 論理は単純です：単語wとsが同じ単語で囲まれていることが多い場合、それらはおそらく同義語です-レーベンシュタインによると、それらの近さを考慮すると、あまり人気のない単語はより人気のある単語の誤ったバージョンである可能性が高いことを意味します。 これらの計算では、以下の言語モデル用に作成されたトライグラム（3語のフレーズ）の出現の統計を使用しました。

言語モデル

したがって、指定された辞書の単語wについて、計算する必要があります $$$P（w）$ -ユーザーによる使用の確率。 最も簡単な解決策は、ある種の大きなケースで単語の出現を取得することです。 一般的に、おそらく、どの言語モデルも、テキストの大きなコーパスを収集し、その中の単語の出現をカウントすることから始まります。 しかし、これに限定すべきではありません。実際、P（w）を計算するとき、単語を修正しようとしているフレーズやその他の外部コンテキストも考慮することができます。 タスクは計算タスクに変わります $$$P（w_1w_2 \ ldots w_k）$ どこの $$$w_i$ -タイプミスを修正し、現在カウントしている単語 $$$P（w）$ そして残り $$$w_i$ -ユーザーリクエストで修正された単語を囲む単語。



それらを考慮に入れる方法を学ぶには、コーパスをもう一度調べて、n-gram、単語シーケンスの統計をコンパイルする価値があります。 通常、制限された長さのシーケンスを取ります。 インデックスを膨らまさないようにトライグラムに限定しましたが、それはすべてあなたの心の強さ次第です（そしてケースのサイズ-トライグラムの統計でさえノイズが多すぎる）。



従来のn-gram言語モデルは次のようになります。 フレーズについて $$$w_1w_2 \ ldots w_k$ その確率は式によって計算されます

$$

$$P（w_1w_2 \ ldots w_k）= P（w_1）\ cdot P（w_2 | w_1）\ cdot P（w_3 | w_1w_2）P（w_k | w_1w_2w_ {k-1}）\ ,,$$

どこで $$$P（w_1）$ -直接単語の頻度、および $$$P（w_3 | w_1w_2）$ -単語の確率 $$$w_3$ 彼が行く前に $$$w_1w_2$ -トライグラム頻度の比以外 $$$w_1 w_2 w_3$ バイグラム周波数へ $$$w_1 w_2$ 。 （この式は、単純にベイズ式を繰り返し適用した結果であることに注意してください。）



つまり、計算したい場合 $$$P（\ text {mom soap frame}）$ の任意のn-gramの頻度を示す $$$f$ 式を取得します

$$

$$P（\ text {mom soap frame}）= f（\ text {mom}）\ cdot \ frac {f（\ text {mom soap}）} {f（\ text {mom}）} \ cdot \ frac { f（\ text {mom soap frame}）} {f（\ text {mom soap}）} = f（\ text {mom soap frame}）\、。$$

論理的ですか？ 論理的です。 ただし、フレーズが長くなると困難が始まります。 ユーザーが印象的な詳細で10語の検索クエリを入力した場合はどうなりますか？ 10グラムすべての統計を保持する必要はありません。これは高価であり、データはノイズが多く、指標ではない可能性があります。 いくつかの制限された長さのn-gram（例えば、すでに上で提案された長さ3）でうまく行きたいです。



ここで、上記の式が役立ちます。 フレーズの最後に出現する単語の確率は、その直前のわずかな単語だけに大きく影響されると仮定しましょう。つまり、

$$

$$P（w_k | w_1w_2 \ ldots w_ {k-1}）\約P（w_k | w_ {k-L + 1} \ ldots w_ {k-1}）\、。$$

パッティング $$$L = 3$ 、より長いフレーズの場合、式が得られます





$$$P（\テキスト{carlはClaraからサンゴを盗んだ}）\約f（\テキスト{carl}）\ cdot \ frac {f（\ text {carl}）} {f（\ text {carl}）} \ cdot \ frac {f（\ text {claraからのカール}）} {f（\ text {carlからの}）} \ cdot \ frac {f（\ text {claraからのストール}）} {f（\ text {からのクララ} ）} \ cdot \ frac {f（\ text {claire stole corole}）}} {f（\ text {claire stole}）} \、。$





注：フレーズは5つの単語で構成されていますが、式には3つ以下のn-gramが表示されます。 これはまさに私たちが目指していたものです。



わずかな瞬間が残りました。 ユーザーが統計に非常に奇妙なフレーズと対応するn-gramを入力し、まったく入力しなかった場合はどうなりますか？ なじみのないN-gramを置くのは簡単だろう $$$f = 0$ この値で割る必要がなかった場合。 ここでは、さまざまな方法で行うことができるスムージング（スムージング）について説明します。 ただし、 Kneser-Neyの平滑化などの深刻なアンチエイリアシングアプローチの詳細な説明は、この記事の範囲をはるかに超えています。

フレーズを修正する方法

実装に移る前に、最後の微妙な点について説明します。 上記で説明した問題の説明は、1つの単語があり、修正する必要があることを暗示しています。 次に、この1つの単語が他のいくつかの単語の中でフレーズの途中にある可能性があり、それらも考慮に入れて最適な修正を選択する必要があることを明確にしました。 しかし、実際には、ユーザーはどの単語のスペルを指定せずにフレーズを送信するだけです。 多くの場合、いくつかの単語またはすべてを修正する必要があります。



多くのアプローチがあります。 たとえば、フレーズ内の単語の左側のコンテキストのみを考慮することができます。 次に、左から右の単語に従って、必要に応じて修正すると、新しい品質のフレーズが得られます。 たとえば、最初の単語がいくつかの一般的な単語のようになり、間違ったオプションを選択した場合、品質は低下します。 フレーズの残りの部分（おそらく最初は完全にエラーがない場合）は、間違った最初の単語に合わせて調整され、元のテキストとはまったく関係のないテキストを取得できます。



[4]で提案されているように、単語を個別に検討し、特定の分類子を適用して、特定の単語が封印されているかどうかを理解することができます。 分類器は、カウント方法をすでに知っている確率、および他の多くの機能についてトレーニングされています。 分類子が修正する必要があることを示している場合、既存のコンテキストを考慮して修正します。 繰り返しますが、複数の単語のスペルが間違っている場合、エラーのあるコンテキストに基づいて最初の単語について決定する必要があり、品質の問題につながる可能性があります。



ガーディアンの実装では、このアプローチを使用しました。 言葉ごとにしましょう $$$s_i$ 私たちのフレーズでは、エラーモデルを使用して、意味のある上位N個の辞書の単語を見つけ、考えられるあらゆる方法でそれらをフレーズに連結します。 $$$N ^ K$ 結果のフレーズ $$$K$ -元のフレーズの単語数、値を正直に計算する

$$

$$P（s_1 | w_1）\ cdot P（s_K | w_K）\ cdot P（s_K | w_K）\ cdot P（w_1w_2 \ ldots w_K）^ {\ lambda} \、。$$

ここに $$$s_i$ -ユーザーが入力した単語、 $$$w_i$ -それらに対して選択された修正（現在、ソート中）、および $$$\ラムダ$ -[4]で提案されている、エラーモデルと言語モデルの比較品質によって決定される係数（大きな係数-言語モデルをより信頼し、小さな係数-エラーモデルをより信頼します）。 全体として、各フレーズについて、対応する辞書のバリエーションで修正される個々の単語の確率を掛け、さらにこれを言語のフレーズ全体の確率で掛けます。 アルゴリズムの結果は、この値を最大化する辞書の単語からのフレーズです。



だから何を止めますか？ ブルートフォース $$$N ^ K$ フレーズ？



幸いなことに、n-gramの長さが制限されているという事実により、すべてのフレーズの最大値をはるかに高速に見つけることができます。 覚えておいてください：上記の式を簡略化しました $$$P（w_1w_2 \ ldots w_K）$ 3以下の長さのn-gramの周波数のみに依存するようになりました。

$$

$$P（w_1w_2 \ ldots w_K）= P（w_1）\ cdot P（w_2 | w_1）\ cdot P（w_3 | w_1w_2）\ cdot \ ldots \ cdot P（w_K | w_ {K-2} w_ {K-1 }）\、。$$

この値に乗算すると $$$P（s_i | w_i）$ そして、最大化しようとします $$$w_K$ 、すべての種類を整理するのに十分であることがわかります $$$w_ {K-2}$ そして $$$w_ {K-1}$ そして彼らのために問題を解決します-つまり、フレーズのために $$$w_1w_2 \ ldots w_ {K-2} w_ {K-1}$ 。 合計すると、問題は動的プログラミングで解決されます $$$O（KN ^ 3）$ 。

実装

ケースをまとめてnグラムを数える

すぐに予約します。複雑なMapReduceを開始するのに十分なデータがありませんでした。 そのため、レビュー、コメント、検索クエリのテキストをすべてロシア語で収集しました（商品の説明は悲しいかな、英語で表示され、自動翻訳の結果の使用は結果を改善するよりもむしろ悪化しました）をサービスから1つのテキストファイルに収集し、カウントするサーバーを夜に設定しました単純なPythonスクリプトを使用したトライグラム。



辞書として、頻度の高い上位の単語を取り上げ、約10万語を得ました。 長すぎる単語（20文字以上）と短すぎる（ハードコードされた有名なロシア語を除く3文字未満）は除外されました。 規則性r"^[a-z0-9]{2}$"



の単語を別にr"^[a-z0-9]{2}$"



バージョンと長さ2の他の興味深い識別子が生き残ったように。



フレーズでバイグラムとトライグラムを数えると、辞書に載っていない単語が発生する場合があります。 この場合、私はこの単語を捨て、2つの部分（この単語の前後）でフレーズ全体を叩き、別々に作業しました。 それでは、 「abyrvalg」とは何かを知っていますか？ これは... HEADMAN、同僚は 「トライグラムを考慮に入れます」知っていますか、「」「何を知っている」、「」「何を知っている」、そしてこれが漁師の主任の同僚です（もちろん、「首長」という言葉が辞書に収まらない限り...）。

エラーモデルをトレーニングする

さらに、Jupyterですべてのデータ処理を実行しました。 n-gramの統計はJSONから読み込まれ、後処理が実行されて、Levenshteinに従って互いに近い単語をすばやく見つけます。ループ内のペアについては、単語を配置し、フォームss→s（スポイラーの下）の短い編集を抽出する（やや面倒な）関数が呼び出されます





編集の計算自体は基本的に見えますが、時間がかかる場合があります。

エラーモデルを適用する

この部分は、Goのマイクロサービスとして実装され、gRPCを介してメインバックエンドに接続されます。 BrillとMoore自身によって記述されたアルゴリズム[2]が、わずかな最適化とともに実装されました。 その結果、著者の主張の約2倍の速度で動作します。 Goか私かを判断する勇気はありません。 しかし、プロファイリングの過程で、Goについて少し新しいことを学びました。

• math.Max
  
  
  
  を使用して最大値をカウントしないでください。 これはif a > b { b = a }
  
  
  
  よりも約3倍遅いです！ この関数の実装を見てください：
  
  

   // Max returns the larger of x or y. // // Special cases are: // Max(x, +Inf) = Max(+Inf, x) = +Inf // Max(x, NaN) = Max(NaN, x) = NaN // Max(+0, ±0) = Max(±0, +0) = +0 // Max(-0, -0) = -0 func Max(x, y float64) float64 func max(x, y float64) float64 { // special cases switch { case IsInf(x, 1) || IsInf(y, 1): return Inf(1) case IsNaN(x) || IsNaN(y): return NaN() case x == 0 && x == y: if Signbit(x) { return y } return x } if x > y { return x } return y }
        
        
  
          
          
          
        
  
      
          
          
          
        
        
  
          
          
          
        
  
      
       

  
  
  突然+0を-0より大きくする必要がある場合をmath.Max
  
  
  
  使用しないでmath.Max
  
  
  
  。
  
  
• 配列を使用できる場合は、ハッシュテーブルを使用しないでください。 もちろん、これは非常に明白なアドバイスです。 トライノードの子孫配列のインデックスとして使用できるように、プログラムの開始時にUnicode文字の番号を番号に変更する必要がありました（このような検索は非常に一般的な操作でした）。
  
  
• ゴーバックコールバックは安くはありません。 コードレビュー中のリファクタリング中に、アルゴリズムが正式に変更されなかったにもかかわらず、デカップリングを試みる私の試みのいくつかは、プログラムを大幅に遅くしました。 それ以来、Go最適化コンパイラには成長の余地があると考えています。
  
  

言語モデルを適用する

ここでは、驚くことなく、上記のセクションで説明した動的プログラミングアルゴリズムが実装されました。 このコンポーネントの作業は最も少なく、最も遅い部分はエラーモデルの適用です。 したがって、これらの2つのレイヤー間では、Redisでのエラーモデルの結果のキャッシュがさらにねじ込まれました。

結果

この作業の結果（約1か月かかりました）に基づいて、ユーザーにA / Bテストガードを実施しました。ガーディアンの導入前にあったすべての検索クエリのうち、空の検索結果の10％の代わりに、それらの5％がありました。基本的に、残りのリクエストはプラットフォーム上にない商品に対するものです。2番目の検索クエリのないセッションの数も増加しました（そしてこの種のUXに関連するいくつかのメトリック）。ただし、金に関連するメトリックは大きく変化しませんでした。これは予想外のことであり、他のメトリックの徹底的な分析とダブルチェックにつながりました。

おわりに

スティーブン・ホーキングはかつて彼が本に含めたすべての式が読者の数を半分にするだろうと言われました。さて、この記事には約50人がいます-おめでとうございます$$10 - 10読者はこの場所に行きます！$10^{-10}$

ボーナス

参照資料

[1]ワシントン州ゲール、KW教会のMDカーニガン。ノイズの多いチャネルモデルに基づくスペル修正プログラム。第13回計算言語学に関する会議の議事録-1990年第2巻。



[2] E.Brill、RCムーア。雑音の多いチャンネルスペル訂正のための改良されたエラーモデル。第38回計算言語学協会に関する第38回年次会議の議事録、2000



。機械翻訳における大言語モデル。自然言語処理の経験的方法に関する2007年会議の議事録。



[4] C.ホワイトロー、B。ハッチンソン、GYチョン、G。エリス。言語に依存しないスペルチェックと自動修正のためのWebの使用。2009年自然言語処理の経験的方法に関する会議の議事録：第2巻。