これはTensorFlowライブラリチュートリアルです。 手書きの数字の認識に関する記事よりも少し深く考えてください。 これは、最適化方法に関するチュートリアルです。 ここでは数学なしではできません。 完全に忘れても大丈夫です。 リコール。 正式な証拠や複雑な結論はなく、直感的な理解に必要な最小限のものだけがあります。 まず、このアルゴリズムがニューラルネットワークの最適化にどのように役立つかについての少しの背景。

6か月前、友人からPythonでニューラルネットワークを作成する方法を示すように頼まれました。 彼の会社は、地球物理学的測定用の機器を製造しています。 掘削中のいくつかの異なるプローブは、井戸を取り巻く環境のパラメーターに関連する信号のセットを測定します。 複雑な場合には、強力なコンピューター上でも長時間にわたって信号から環境のパラメーターを正確に計算し、現場での測定結果を解釈する必要があります。 クラスター上の数十万のケースをカウントし、それらのニューラルネットワークをトレーニングするというアイデアがありました。 ニューラルネットワークは非常に高速であるため、掘削のプロセスで、測定された信号と一致するパラメータを決定するために使用できます。 詳細は記事にあります:
Kushnir、D.、Velker、N.、Bondarenko、A.、Dyatlov、G.、&Dashevsky、Y.(2018、October 29)。 ニューラルネットワーク(ロシア語)を使用した2D障害モデルでの深方位抵抗率ツールのリアルタイムシミュレーション。 石油技術者協会。 土井:10.2118 / 192573-RU
ある晩、私はケラスが単純なニューラルネットワークを実装する方法を示し、職場の友人がカウントされたデータのトレーニングを開始しました。 数日後、結果について話し合いました。 私の観点からは、彼は有望そうに見えましたが、友人は、デバイスの精度で計算が必要だと言いました。 そして、 平均二乗誤差が約1であることが判明した場合、1e-3が必要でした。 3注文少ない。 千回。
ニューラルネットワークアーキテクチャ、データの正規化、および最適化アプローチの実験では、ほとんど何も得られませんでした。 数週間後、友人から電話があり、MatLabをインストールし、 Levenberg-Marquardt法(以下LMと呼びます)によって問題を解決したと言われました。 長時間(数日間)最適化され、GPUでは機能しませんでしたが、結果は正しいものでした。 それは挑戦のように聞こえました。
kerasまたはTensorFlowの既製LMオプティマイザーのクイック検索が失敗しました。 私はpyrennライブラリのみに出会いましたが、その機能は貧弱に思えました。 自分で実装することにしました。 一見、すべてがシンプルに見え、2晩で十分だったはずです。 時間がかかりました。 次の2つの問題がありました。
- TensorFlow。 たくさんの記事がありますが、ほとんどすべてのレベルは「しかし、
こんにちは世界の手書き数字認識を書きましょう。」 - 数学 私は多くのことを忘れていました。数学の記事の著者は、私のような人々をまったく気にしません。
その結果、数学を忘れ、TensorFlowをもう少し深く理解したいが、筋金入りではない人のために記事を書きました。 この記事には多くのテキストと小さなコードがあります。 反対のオプションは、テキストが少なくコードが多い場合、 Jupyter Notebook Levenberg-Marquardtです。
Rosenbrock機能について知る
最適化アルゴリズムのベンチマークとしてよく使用されるRosenbrock関数によってトレーニングデータを生成します。
f ( x 、 y ) = ( a - x ) 2 + b ( y - x 2 ) 2
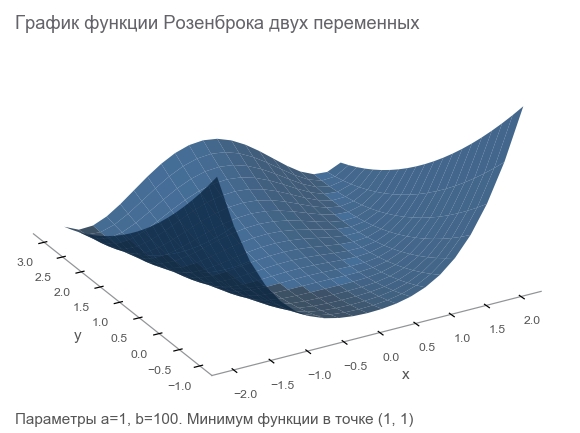
なぜ彼女はいいの?
- 美しいスケジュール。 ローゼンブロック渓谷と呼ばれ、翻訳不能なローゼンブロックのバナナ機能です。
- グローバルな最小値は、長くて狭く、放物線状の平坦な谷の中にあります。 谷を見つけることは簡単であり、グローバルな最小値を見つけることは困難です。
- 多次元オプションがあります。 多くの変数に適した関数を見つけるのはそれほど簡単ではありません。
さらなる作業に必要なライブラリを接続することで、コードの記述を開始します。
import numpy as np import tensorflow as tf import math def rosenbrock(x, y, a, b): return (a - x)**2 + b*(y - x**2)**2
問題を述べる
測定デバイスについて話していたので、アナロジーを使い続けましょう。 架空の世界のデバイスは座標を測定できます ( X 、 y ) と高さ z 。 物理学者は世界を研究し、「 はい、これはローゼンブロックです!座標を知っていれば、高さを正確に計算できます。測定する必要はありません。 」 言い換えれば、科学者は私たちにモデルを与えました z = r o s e n b r o c k ( x 、 y 、 a 、 b ) パラメータに依存します ( A 、 b ) 。 これらのパラメーターは、架空の世界では一定ですが、不明です。 それらを見つける必要があります。
私たちは一連の実験を行い、 m ポイント (x1、y1、z1)、(x2、y2、z2)、...、(xm、ym、zm) :
# (2.5, 2.5) - , , data_points = np.array([[x, y, rosenbrock(x, y, 2.5, 2.5)] for x in np.arange(-2, 2.1, 2) for y in np.arange(-2, 2.1, 2)]) m = data_points.shape[0]
最適化する最初の方法は、パラメーターを試して推測することです。 Numpyライブラリを使用します。
x, y = data_points[:, 0], data_points[:, 1] z = data_points[:, 2] # =5 b=5? a_guess, b_guess = 5., 5. # -hat , , # , , . # ^ - # . hat. z_hat = rosenbrock(x, y, a_guess, b_guess)
私たちがいかに間違っているかを理解するには? 残差をカウント-エラーサイズ。 m ポイントが与える m 矛盾-積分インジケータが必要です。 各残差を二乗して二乗し、平均を計算します。
MSE(a、b)= frac1m summi=1(zi− widehatzi)2
このような近接度の尺度は、 平均二乗誤差と呼ばれます ( 平均二乗誤差 、以下、 mseと呼びます )。
# r - residuals () r = z - z_hat # mse loss = np.mean(r**2) print(loss)
[Out]: 3868.2291666666665
mseを最小化することにより、最小二乗問題を解きます( 非線形二乗最小化 )。
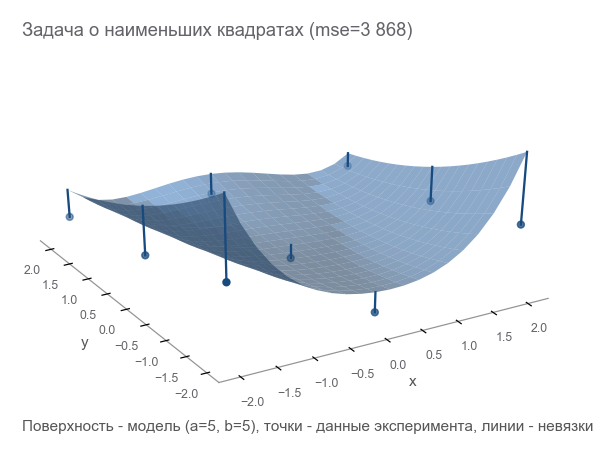
パラメータがまったく推測しなかったことがわかります。
TensorFlowで問題を定式化する
モデルの形式は z=rosenbrock(x、y、a、b) 。 フォームに持ってきます y=f(x、p) (通常は数学の書き込み \ベータ の代わりに p プログラマーはベータ版を使用しません)。 モデルは次の形式を持ちます y=rosenbrock(x、p) どこで y -高さ x 2つの要素(コンポーネント) の座標ベクトルであり、 p -パラメータのベクトル 。
プログラマーは、ベクターを1次元配列と考えることがよくあります。 これは完全に正しいわけではありません。 数値の配列は、ベクトルを表す手段です。 ベクトルを次元の配列として表すことができます N 、二次元配列 1\回N 、さらには配列 N\回1 ベクトルが列ベクトルであるという事実(たとえば、マトリックスを乗算する)が重要な場合:
beginbmatrixx1 vdotsxN endbmatrix
TensorFlowはtensorの概念を使用します。 テンソルは、配列と同様に、1次元( ベクトルを表す)、2次元( 行列または列ベクトル )、およびそれ以上の次元にできます。
# ('placeholder' , # ) x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m]) # ('variable' , ) # (5, 5) p = tf.Variable([5., 5.], dtype=tf.float64) # y_hat = rosenbrock(x[:, 0], x[:, 1], p[0], p[1]) # r = y - y_hat # mse (mean squared error) loss = tf.reduce_mean(r**2)
TensorFlowコードは、Numpyコードと形式に違いはありません。 内容は膨大です。 Numpyコードは mse 値を計算します 。 TensorFlowコードは計算をまったく実行せず、mse が計算できる データフロー グラフを形成します 。 非常に脳に寛容な瞬間は、 rosenbrock関数の働きです。 両方の場合に使用します。 ただし、Numpy配列を渡すと、式に従って計算が実行され、数値が返されます。 そして、テンソルをTensorFlowに転送すると、データストリームのサブグラフを形成し、テンソルの形でエッジを返します。 多型の奇跡、しかしそれらを乱用しないでください:
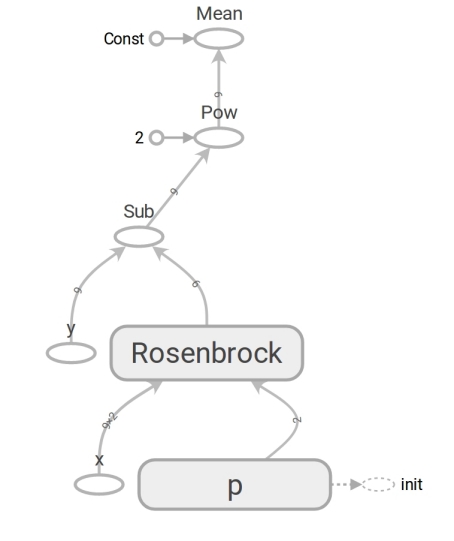
このようなデータフローグラフが存在するため、特にTensorFlowは自動的に微分を計算できます( リバースモードの自動微分手法を使用)。
数学の瞬間。 「忘れた人のための」ブロックはネタバレに隠されます。
ほとんどの場合、1つの変数のスカラー(数値を返す)関数の微分の定義を覚えています。 f: mathbbR\右矢印 mathbbR 派生物 f その時点で x in mathbbR 定義:
f′(x)= limh to0 fracf(x+h)−f(x)h
デリバティブは変化を測定する方法です。 スカラーの場合、導関数は関数がどれだけ変化するかを示します f もし x 小さな値に変更する \バレプシロン :
f(x+ varepsilon)\約f(x)+ varepsilonf′(x)
便宜上、 y=f(x) 、および導関数 y によって x 方法を書きます frac partialy partialx 。 そのような記録は、それを強調しています frac partialy partialx -変数間の変化率 x そして y 。 より具体的には、 x に変更 \バレプシロン それから y およそに変更 varepsilon frac partialy partialx 。 次のように書くこともできます:
x\右矢印x+\デルタx\右矢印y\右矢印\近似y+ frac partialy partialx Deltax
読み取り:「変化する x に x+\デルタx 変わる y およそ y+ Deltax frac partialy partialx 「。このような記録は、変更間のリンクを明確に強調しています x そして変化 y 。
データフローグラフを作成し、mse計算を実行しましょう。
# # placeholder ( ) feed_dict = {x: data_points[:,0:2], y: data_points[:,2]} # TensorFlow session = tf.Session() # session.run(tf.global_variables_initializer()) # () loss (mse) current_loss = session.run(loss, feed_dict) print(current_loss)
[Out]: 3868.2291666666665
結果はNumpyの場合と同じです。 だから彼らは間違っていなかった。
最適化を開始
残念ながら、パラメータを推測することはできませんでした。 しかし、その後:
- 最適性の基準-mseの最小値を設定します。
- 可変パラメーターが決定されました:ベクトル p コンポーネント付き a 、 b Rosenbrock関数。
- 制限についてはまだ考えていませんが、制限はありません。
最後のステップでは、有限損失テンソル( 損失 関数 )を使用してデータフローグラフを作成しました。 最適化の目標は、パラメーターベクトルの値を見つけることです。 p 損失関数の値は最小になります。 幸運なことに、この関数のグラフは非常にシンプルです(凹面で、極小値なし):
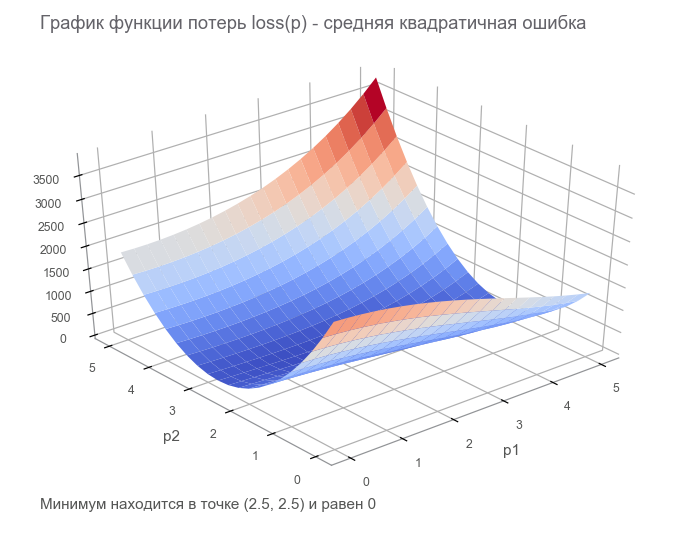
最適化の開始。 まず、一般化されたループを記述します。
# : mse, , # mse, placeholder def train(target_loss, max_steps, loss_tensor, train_step_op, inputs): step = 0 current_loss = session.run(loss_tensor, inputs) # while current_loss > target_loss and step < max_steps: step += 1 # 1, 2, 4, 8, 16... if math.log(step, 2).is_integer(): print(f'step: {step}, current loss: {current_loss}') # session.run(train_step_op, inputs) current_loss = session.run(loss_tensor, inputs) print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}')
最速勾配降下法(SGD)の方法で最適化する
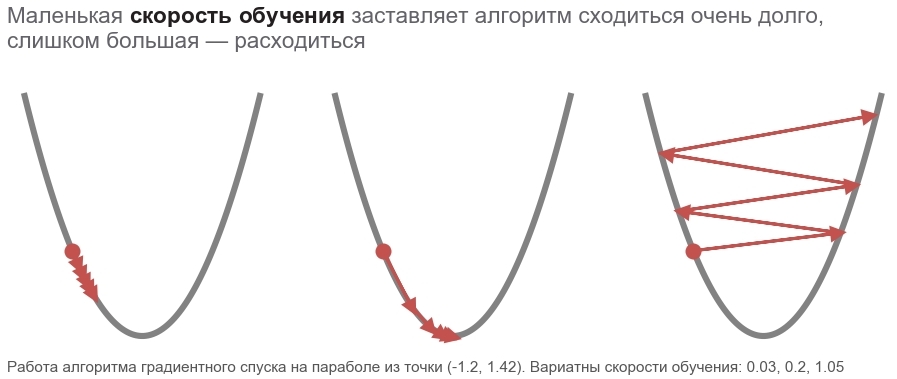
この方法のアクションは、常に斜面を(最も急な方向に)降ろす大胆なスキーヤーに乗ることと比較できます。 この場合、位置のポイントの勾配のみが考慮されます。 斜面が強い場合、スキーヤーは次の変更の前に長い距離を飛行します。 弱い勾配では、小さなステップで移動します。 たぶん飛び去る方法 木に ( アルゴリズムは発散します )、ピットに閉じ込められます( 極小値 )。

次のように書くことができます(変更 boldsymbolp に boldsymbolp−... ):
boldsymbolp rightarrow boldsymbolp− alpha[ nablaploss( boldsymbolp)]
脂っこい boldsymbolp これは実際の位置のポイント、つまり現在のステップでのパラメーターベクトルの値であることを強調します。 最初のステップでは、これが推測です(5、5)。 式には2つの興味深い点があります。 alpha - 学習率 ( 学習率 )、 nablap損失 -パラメーターベクトルによる損失関数の勾配 ( gradient )。
入力としてベクトルを受け取り、スカラーを生成する関数を考えてみましょう。 f: mathbbRN\右矢印 mathbbR 。 デリバティブ f その時点で x in mathbbRN 現在は勾配と呼ばれ、ベクトルです [ nablaxf(x)] in mathbbRN (「nabla」と読みます) 偏微分で構成されます:
nablaxy=( frac partialy partialx1、 frac partialy partialx2、...、 frac partialy partialxN)
この場合、関数の変更が引数の変更に依存するという記録は、次の形式になります。
x\右矢印x+\デルタx\右矢印y\右矢印\約y+ nablaxy cdot\デルタx
記録はそれを考慮してかなり変更されました x 、 \デルタx そして nablaxy -ベクトルの mathbbRN 、そして y -スカラー。 ベクトルを乗算するとき nablaxy そして \デルタx スカラー積が使用されます (コンポーネントの積の合計)。
# grad = tf.gradients(loss, p)[0] # learning_rate = 0.0005 # , apply_gradients - # opt = tf.train.GradientDescentOptimizer(learning_rate=1) # sgd = opt.apply_gradients([(learning_rate*grad, p)]) # , 40000 session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, sgd, feed_dict) print('PARAMETERS:', session.run(p))
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 1381.5379689135807 [...] ENDED ON STEP: 582, FINAL LOSS: 9.698531012270816e-11 PARAMETERS: [2.50000205 2.49999959]
582ステップかかりました。
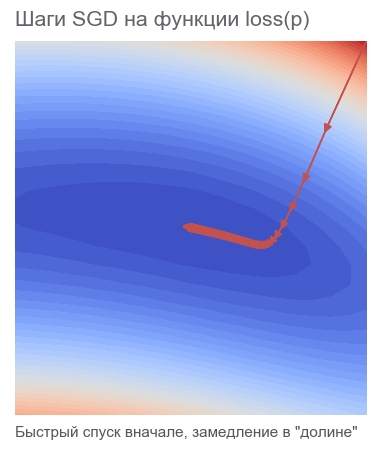
なぜ勾配と反対の方向に移動するのですか? スカラー積でエントリを思い出してください: x\右矢印x+\デルタx\右矢印y\右矢印\約y+ nablaxy cdot\デルタx 。 最小化 y 。 関数の振る舞いは導関数を介して小さな近傍でのみ既知であるため、積を最小化する小さいながら最適なステップで移動する必要があります。 nablaxy cdot Deltax 。 学校の定義では、2つのベクトルのスカラー積は、これらのベクトルの長さとベクトル間の角度の余弦の積に等しい数です。 a cdotb= left|a right| left|b right|cos angle(a、b) 。 ベクトルの固定長の場合、この積は-1のコサインで最小になります。 ベクトルが反対方向に向けられている場合、180度の角度で。 したがって、最小のスカラー積 nablaxy cdot Deltax 達成されたとき \デルタx 反勾配の方向に。
Adamメソッドで最適化
勾配法についてはこれ以上説明しませんが、多くのバリエーションがあります。 それらについては記事「 ニューラルネットワークの最適化の方法」で読むことができます。 TensorFlowでは、多くのオプティマイザーが既に実装されています。 たとえば、アダム:
# , # adm = tf.train.AdamOptimizer(15).minimize(loss) # , 40000 session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, adm, feed_dict) print('PARAMETERS:', session.run(p))
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 34205.72916492336 [...] ENDED ON STEP: 317, FINAL LOSS: 2.424142714263483e-12 PARAMETERS: [2.49999969 2.50000008]
317ステップで管理。 はるかに高速。
ニュートンの方法で最適化する
二次法の動作は、ルートの次のポイントを長時間熟考し、その場所の傾斜だけでなく曲率も考慮に入れる合理的なフリーライドスノーボーダーに乗ることと比較できます。

実際、勾配降下法と2次法はどちらも、現在の点で関数を推測( 近似 )しようとします。 勾配法は、ある点での関数グラフの勾配( 1次導関数)のみに焦点を合わせます。 二次法は、バイアスに加えて、 曲率を考慮に入れます。二次導関数:「曲率が持続する場合、最小値はどこになりますか?」 計算してそこに行きます:
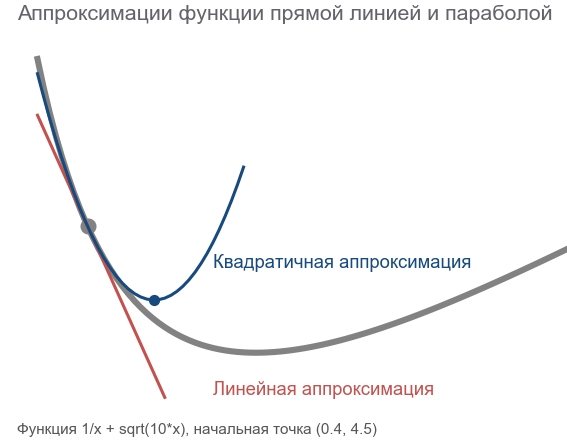
このような近似を構築し、推定最小点を計算するには、 テイラー級数を使用できます。 1次元の場合、点での2次多項式による近似 a 次のようになります。
f(x)\約f(a)+ fracf′(a)(x−a)1!+ fracf″(a)(x−a)22!
最小値は x=a− fracf′(a)f″(a) 。 多次元のケースはより深刻に見えます。
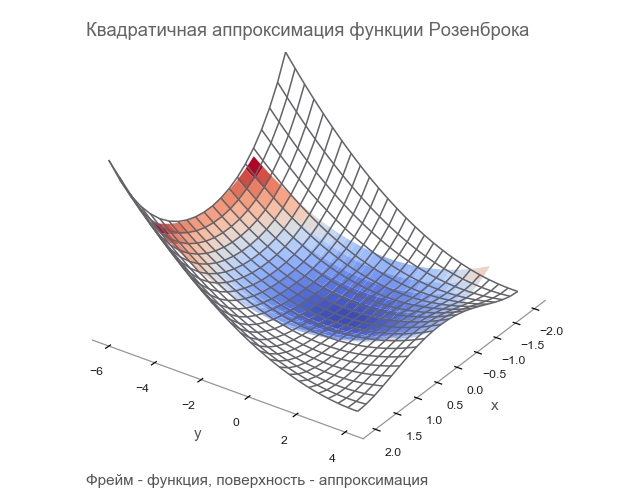
ヘッセ行列は、2次導関数で構成される正方行列です。
boldsymbolHyx= beginbmatrix frac partial2y partialx21& frac partial2y partialx1 partialx2& cdots& frac partial2y partialx1 partialxN frac partial2y partialx2 partialx1& frac partial2y partialx22& cdots& frac partial2y partialx2 partialxN vdots& vdots& ddots& vdots frac partial2y partialxN\部分x1& frac partial2y partialxN partialx2& cdots& frac partial2y partialx2N endbmatrix
点での勾配とヘッセ行列を通るベクトルの関数の二次多項式による近似 a 次のようになります。
f(x)\約f(a)+(xa) intercal[ nablaxf(a)]+ frac12!(xa) intercal[ boldsymbolHfx(a)](xa)
最小値は x=a−[ boldsymbolHfx(a)]−1[ nablaxf(a)] 。 形状は1次元の場合とほぼ一致します。1次導関数を勾配に、2次導関数をヘッセ行列に置き換え、ベクトルを操作するための修正を行いました。 ベクトルを行列で除算することは不可能であるため、 逆行列による乗算が使用されます。 Tは転置を意味します。 この式は、デフォルトではベクトルが列であることを意味します。 転置は、列 ベクトルを行ベクトルに変換します。 TensorFlowで実装する場合、これを考慮に入れる必要がありますが、反対の方向:デフォルトでは、ベクトルは文字列(1次元テンソル)です。 念のため、転置は90度の回転ではなく、行を同じ順序で列に変換することです。
そのため、Newtonメソッドのステップの形式は次のとおりです。
boldsymbolp rightarrow boldsymbolp−[ boldsymbolHlossp( boldsymbolp)]−1[ nablaploss( boldsymbolp)]
TensorFlowには、このメソッドを実装するためのすべてがあります。
# hess = tf.hessians(loss, p)[0] # - grad_col = tf.expand_dims(grad, -1) # , dp = tf.matmul(tf.linalg.inv(hess), grad_col) # - - dp = tf.squeeze(dp) # p dp newton = opt.apply_gradients([(dp, p)]) # , 40000 session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, newton, feed_dict) print('PARAMETERS:', session.run(p))
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 105.04357496954218 step: 4, current loss: 9.96663526704236 ENDED ON STEP: 6, FINAL LOSS: 5.882202372519996e-20 PARAMETERS: [2.5 2.5]
十分な6つのステップ:
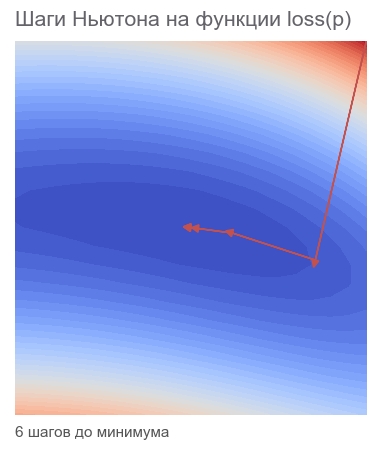
Gauss-Newtonアルゴリズムにより最適化
ニュートン法には1つの欠点があります-ヘッセ行列です。 TensorFlowのおかげで、1行のコードでカウントできます。 wikiによると、 Johann Karl Friedrich Gaussは1809年に彼の方法について最初に言及しました。 その場合、最小二乗法のいくつかのパラメーターのヘッセ行列の計算には多くの時間がかかります。 これで、Gauss-Newtonアルゴリズムは計算を簡素化するために、 ヤコビ行列を介した ヘッセ 行列の近似を使用すると仮定できます。 しかし、歴史の観点からすると、これはそうではありません。 ルートヴィヒオットーヘッセ (彼にちなんで命名されたマトリックスを開発した)は、アルゴリズムの最初の言及から2年後の1811年に生まれました。 カール・グスタフ・ヤコビは5歳でした。
Gauss-Newtonアルゴリズムは、損失関数では機能しません。 残差関数で動作します r(p) 。 この関数は、パラメータの入力ベクトルを受け取ります p そして、残差ベクトルを返します。 私たちの場合、ベクトル p 2つのコンポーネント(パラメーター a そして b ローゼンブロック関数)、およびからの残差ベクトル m コンポーネント(実験の数による)。 ベクトル引数のベクトル関数が取得されます。 その派生物:
ベクトルを入力として受け取り、ベクトルも生成する関数を考えてみましょう。 f: mathbbRN\右矢印 mathbbRM 。 デリバティブ f その時点で x 今サイズがあります N\回M 、 ヤコビ行列と呼ばれ、偏微分のすべての組み合わせで構成されます。
boldsymbolJyx= beginpmatrix frac partialy1 partialx1& cdots& frac partialy1\部分的なxN vdots& ddots& vdots frac partialyM partialx1& cdots& frac partialyM partialxN endpmatrix
ヤコビ行列の行が成分の勾配であることがわかります y 。 アイテム (i、j) 行列 frac partialy partialx 等しい frac partialyi partialxj どれくらい変化するかを教えてくれます yi 変更するとき xj 小さい値。 前の場合と同様に、次のように記述できます。
x\右矢印x+\デルタx\右矢印y\右矢印\約y+\太字Jyx\デルタx
ここに boldsymbolJyx 行列 N\回M 、そして \デルタx サイズベクトル N したがって、製品 boldsymbolJyx Deltax 行列とベクトルの積で、サイズがベクトルになります M 。
豊富なキャラクターで混乱しないように、 boldsymbolJr -現在の点での残差関数のヤコビ行列 boldsymbolp 。 次に、Gauss-Newtonアルゴリズムは次のように記述できます。
boldsymbolp rightarrow boldsymbolp−[ boldsymbolJ rintercal boldsymbolJr]−1 boldsymbolJ rintercalr( boldsymbolp)
フォームでの録音は、ニュートンの方法の録音と完全に一致します。 ヘッセ行列の代わりにのみ使用されます boldsymbolJ rintercal boldsymbolJr 勾配の代わりに boldsymbolJ rintercalr( boldsymbolp) 。 次に、このような近似を使用できる理由を確認します。 それまでの間、TensorFlowの実装に進みましょう。
# , TensorFlow , # , # . , : # 1) tf.unstack(r) # 2) tf.gradients(r_i, p) # 3) tf.stack # , # j = tf.stack([tf.gradients(r_i, p)[0] for r_i in tf.unstack(r)]) jT = tf.transpose(j) # - r_col = tf.expand_dims(r, -1) # hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r_col) # , dp = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) # - - dp = tf.squeeze(dp) # p dp ng = opt.apply_gradients([(dp, p)]) # , 40000 session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, ng, feed_dict)
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 14.653025157673625 step: 4, current loss: 4.3918079172783016e-07 ENDED ON STEP: 4, FINAL LOSS: 3.374364957618591e-17 PARAMETERS: [2.5 2.5]
十分な4つのステップ。 ニュートン法よりも小さい。
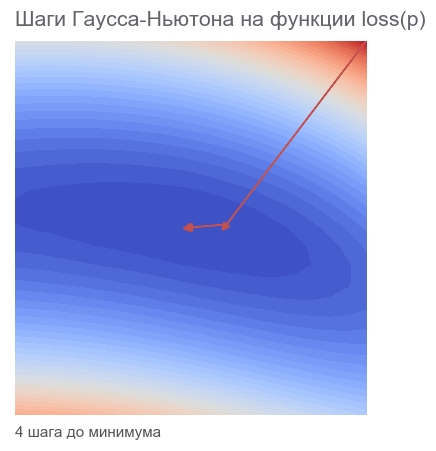
コードからわかるように、損失関数は最適化では使用されず、基準の停止とロギングにのみ使用されます。 最適化アルゴリズムは、どの関数を最小化するかをどのようにして知るのですか 答えは驚くべきことです。 Gauss-Newtonは、 平均二乗誤差のみを最小化します 。
記事の数学的な部分を修正する
必要なすべての計算を繰り返しました。 プログラミングとTensorFlowのみにさらに集中するために、少し修正しましょう。 数学的アクションのシーケンスを追跡するために鉛筆が必要な場合があります。
モデルがあります y=f(x、p) どこで x -ベクトル p -次元パラメーターのベクトル n 、そして y -スカラー。 受け取った実験から m ポイント (x1、y1)、...、(xm、ym) ( データペア )。 残差ベクトル関数は、パラメーターベクトルのみに依存します。 r(p)=(r1(p)、...rm(p)) どこで rk(p)=yk− widehatyk=yk−f(xk、p) 。 , p , xk,yk ? 事実は xk,yk , .
p , ( sum of squared error — sse residual sum-of-squares — rss ) . mse sse , m 。 . :
loss(p)=r21(p)+⋯+r2m(p)=m∑k=1r2k(p)
p (p) 。
, . — . — , r2 等しい 2r∂r∂p 。 :
∇ploss=(m∑k=12rk∂rk∂p1,⋯,m∑k=12rk∂rk∂pn)
. :
[Hlossp]ij=∂2loss∂pi∂pj=m∑k=1(2∂rk∂pi∂rk∂pj+2rk∂2rk∂pi∂pj)
. , , (uv)′=u′v+uv′ 。
いいね! .
, , , — 2rk∂2rk∂pi∂pj 。 , , rk , . — . , ? -.
:
Jr=(∂r1∂p1⋯∂r1∂pn⋮⋱⋮∂rm∂p1⋯∂pm∂pn)
, , . , :
2J⊺rJr≈Hlossp
"" . ( ). , — 2rk∂2rk∂pi∂pj , .
( ):
2J⊺rr=∇ploss
, , - — , mse .
. , , . m (x1,y1),...,(xm,ym) , y=rosenbrock(x,p) 。 p , .
, : " . - ! ". , , , ( supervised learning ). , . : ( training set ) — ; — ( prediction model ) ; — , .
( multi-layer perceptron neural network mlp ). , , :
- ( starting values ) . Xavier'a, .
- ( overfitting ). — . , . — .
- ( scaling of the input ). , .
9 . 500:
# def get_random_rosenbrock_data_points(m): result = np.zeros((m, 3)) result[:, 0] = np.random.uniform(-2, 2, m) result[:, 1] = np.random.uniform(-2, 2, m) result[:, 2] = rosenbrock(result[:, 0], result[:, 1], 2.5, 2.5) return result m = 500 data_points = get_random_rosenbrock_data_points(m) # overfitting , validation_data_points = get_random_rosenbrock_data_points(m)
500 . — ( learner ), ( outcome measurement ) ( features ) .
( network diagram ). MatLab:
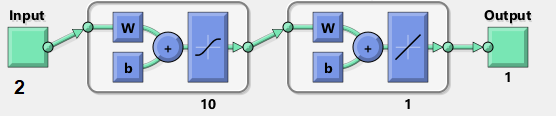
( input ). W ( weights ) 2x10, b ( bias ) 10, ( activation ). () ( hidden layer ) 10 . , , ( output ).
, , ( tanh ):
h1=tanh(xW1+b1)ˆy=h1W2+b2
:
h1=tanh([x1x2][w(1)1,1⋯w(1)1,10w(1)2,1⋯w(1)2,10]+[b(1)1⋯b(1)10])ˆy=[h(1)1⋯h(1)10][w(2)1,1⋮w(2)1,10]+b2
. W1 "" h1 , - W2 。 41 . , .
m×2 , . - ˆy から m :
# 10 "" n_hidden = 10 # Xavier'a initializer = tf.contrib.layers.xavier_initializer() # x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m, 1]) # W1 = tf.Variable(initializer([2, n_hidden], dtype=tf.float64)) b1 = tf.Variable(initializer([1, n_hidden], dtype=tf.float64)) # , tanh h1 = tf.nn.tanh(tf.matmul(x, W1) + b1) # W2 = tf.Variable(initializer([n_hidden, 1], dtype=tf.float64)) b2 = tf.Variable(initializer([1], dtype=tf.float64)) # y_hat = tf.matmul(h1, W2) + b2 # r = y - y_hat # mse loss = tf.reduce_mean(tf.square(r)) # placeholder feed_dict = {x: data_points[:,0:2], y: data_points[:,2:3]} validation_feed_dict = {x: validation_data_points[:,0:2], y: validation_data_points[:,2:3]}
Adam
Adam rosenbrock 。 mse :
# adm = tf.train.AdamOptimizer(1e-2).minimize(loss) session.run(tf.global_variables_initializer()) # , 40000 train(1e-10, 40000, loss, adm, feed_dict) print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict)))
[Out]: step: 1, current loss: 671.4242576535694 [...] ENDED ON STEP: 40000, FINAL LOSS: 0.22862158574440725 VALIDATION LOSS: 0.29000289644978866
. : , , .
rosenbrock 2 . :
- データ。 9 , 500. .
- パラメータ - p , .
:
# y x def jacobian(y, x): loop_vars = [ tf.constant(0, tf.int32), tf.TensorArray(tf.float64, size=m), ] # - # _, jacobian = tf.while_loop( lambda i, _: i < m, # # (-), x lambda i, res: (i+1, res.write(i, tf.reshape(tf.gradients(y[i], x), (-1,)))), loop_vars) # return jacobian.stack() # r_flat = tf.squeeze(r) # # parms = [W1, b1, W2, b2] parms_sizes = [tf.size(p) for p in parms] j = tf.concat([jacobian(r_flat, p) for p in parms], 1) jT = tf.transpose(j) # hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r)
Jrp . , 4 W1,b1,W2,b2 。 4 JrW1,Jrb1,JrW2,Jrb2 tf.concat .
. tf.while_loop , ri , , stack .
ri W1 次のようになります。 [∂ri∂w(1)1,1⋯∂ri∂w(1)1,10∂ri∂w(1)2,1⋯∂ri∂w(1)2,10] 。 tf.reshape (-1,) [∂ri∂w(1)1,1⋯∂ri∂w(1)1,10∂ri∂w(1)2,1⋯∂ri∂w(1)2,10] 。
. - . — TensorFlow . — - - W1,b1,W2,b2 。 -. Levenberg-Marquardt Jupyter Notebook rosenbrock_train.py . , TensorFlow . - , ( ) , , .
-
hess_approx grad_approx -. rosenbrock , . :
- : Δp=[Δw(1)1,1⋯Δw(1)2,10Δb(1)1⋯Δb(1)10Δw(2)1,1⋯Δw(2)1,10Δb2]
- :
ΔW1=[Δw(1)1,1⋯Δw(1)2,10] 、 Δb1=[Δb(1)1⋯Δb(1)10] 、 ΔW2=[Δw(2)1,1⋯Δw(2)1,10] 、 Δb2=[Δb2] 。 - , :
ΔW1=[Δw(1)1,1⋯Δw(1)1,10Δw(1)2,1⋯Δw(1)2,10] 、 ΔW2=[Δw(2)1,1⋮Δw(2)1,10] - .
# 1. dp_flat = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) # 2. dps = tf.split(dp_flat, parms_sizes, 0) # 3. for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4. : gn = opt.apply_gradients(zip(dps, parms)) # session.run(tf.global_variables_initializer()) train(1e-10, 100, loss, gn, feed_dict)
[Out]: step: 1, current loss: 548.8468777701685 step: 2, current loss: 49648941.340197295 InvalidArgumentError: Input is not invertible.
- . , . - , .
, .
-
. Matlab trainlm . . MathWorks.
- : p→p−[J⊺rJr]−1J⊺rr(p) 。 - :
p→p−[J⊺rJr+μI]−1J⊺rr(p)
mu I n ( ). mu , -. , . , LM -.
:
mu = tf.placeholder(tf.float64, shape=[1]) n = tf.add_n(parms_sizes) I = tf.eye(n, dtype=tf.float64) # 1. dp_flat = tf.matmul(tf.linalg.inv(hess_approx + tf.multiply(mu, I)), grad_approx) # 2. dps = tf.split(dp_flat, parms_sizes, 0) # 3. for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4. : lm = opt.apply_gradients(zip(dps, parms))
mu ? LM - . , . , mu , . — , mse . , :
# store = [tf.Variable(tf.zeros(p.shape, dtype=tf.float64)) for p in parms] # TensorFlow save_parms = [tf.assign(s, p) for s, p in zip(store, parms)] restore_parms = [tf.assign(p, s) for s, p in zip(store, parms)] # mu 3. feed_dict[mu] = np.array([3.]) step = 0 session.run(tf.global_variables_initializer()) # mse current_loss = session.run(loss, feed_dict) # 100 while current_loss > 1e-10 and step < 100: step += 1 # 1, 2, 4... if math.log(step, 2).is_integer(): print(f'step: {step}, mu: {feed_dict[mu][0]} current loss: {current_loss}') # session.run(save_parms) # , mse while True: # session.run(lm, feed_dict) new_loss = session.run(loss, feed_dict) if new_loss > current_loss: # - mu 10 feed_dict[mu] *= 10 session.run(restore_parms) else: # - mu 10 feed_dict[mu] /= 10 current_loss = new_loss break print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}') print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict)))
[Out]: step: 1, mu: 3.0 current loss: 692.6211687622557 [...] ENDED ON STEP: 100, FINAL LOSS: 0.012346989371823602 VALIDATION LOSS: 0.01859463694102034
100 LM mse 10 , 40 .
. , . , rosenbrock_train.py .
2D . . . , " " ( curse of dimentionality , Bellman, 1961). . .
:
f(x)=N−1∑i=1[100(xi+1−x2i)2+(1−xi)2],x=[x1⋯xN]∈RN
rosenbrock_train.py get_rand_rosenbrock_points .
-
- : " ! 4 , 300! ". , ( ) -. , , . - . . : ? , . . , - :
- 10 000 6D .
- 3 12, 10, 8 (311 ).
- .
- 3.5 .
. - 2 . LM . 20 .
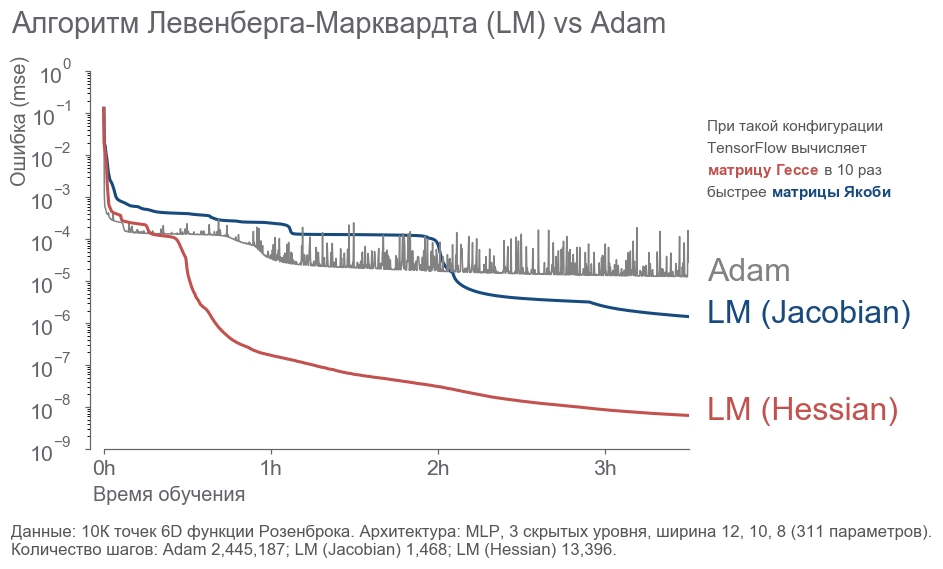
rosenbrock_train.py . . , .
おわりに
, . " ", , . , . , 273 . - , .
, :
- .
- ( ) -:
[1] Petros Drineas, Ravi Kannan, and Michael W. Mahoney. 2006. Fast Monte Carlo Algorithms for Matrices I: Approximating Matrix Multiplication. SIAM J. Comput. 36, 1 (July 2006), 132-157. DOI= http://dx.doi.org/10.1137/S0097539704442684
[2] Adelman, M., & Silberstein, M. (2018). Faster Neural Network Training with Approximate Tensor Operations. CoRR, abs/1805.08079.
, - . , . "".