アレスタの説明のソースは、Lafore R。:L29 Javaのデータ構造とアルゴリズムの説明になります。 古典的なコンピューター科学。 第2版 -SPb。:Peter、2013。-ただし、この問題や他の一般的に使用されるアルゴリズムで最も人気があり適切な704秒。
つまり、異なるアルゴリズムを異なるイデオロギーと比較します。
式(OPN)の一連の作業を視覚化するために、158ページに次のグラフを示します。

すでにここで、シンボル情報の順次読み取りの人の特性について、アルゴリズムの間違った調整を見ることができます。 人にとっては、表現フラグメントの優先度の割り当てと、これらのフラグメントの優先度に応じたさらなる計算スキームの構築がより特徴的です。 したがって、この場合、スキームは実際には次のようになります。
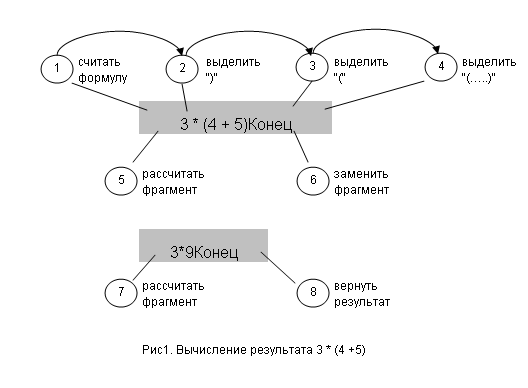
ご覧のとおり、式の文字ごとの解析に関する誤った初期メッセージは、挿入記法処理の歪みを引き起こすだけでなく、複数の括弧を使用した複雑な数式の実際の分析の状況を大幅に複雑にします。 結局、2番目のスキーム(図1)は、分析されたソースの図4.15に示されているものよりも明確であり、かなり短いものです。
さらに、ソースからのかなり長い引用を引用することを余儀なくされており、「フクロウは地球に引っ張られている」。
「ご覧のとおり、中置算術式の結果を計算するプロセスでは、式を前後に移動する必要があります。 最初に、オペランドと演算子は左から右に読み取られます。 演算子の使用に十分な情報が蓄積されると、反対方向に動き始め、2つのオペランドと演算子を「記憶」し、算術演算を実行します。 演算子の後に、優先度の高い別の演算子または括弧が続く場合、演算子の使用は延期されます。 この場合、次に優先度の高い演算子が最初に適用され、次に(左に)戻って以前の演算子が適用されます。順方向と逆方向に移動することから始めましょう。 事実、OPNの謝罪者は通常、計算の最後の段階に集中します。すでに並べ替えられた文字が積み重ねられてそこから削除されると、もちろんこの段階は非常に効果的です。 しかし、結局のところ、延滞の作業は2つの段階で構成されています(p。153)。
もちろん、このような処理を実行するアルゴリズムは直接プログラムできますが、前述のように、最初に式を後置レコードに変換する方が簡単です。」(引用の終わり)
「1。 算術式を後置記法と呼ばれる別の形式に変換します。おっと! 彼らは第2段階の利点を押し出そうとしますが、第1段階の頭痛は単に控えめに言及されています。 これは著者へのb責ではなく、著者はクールだと書いている。これは、このやや泥だらけの方法が式の分析において主要な方法と考えられ、対応する専門分野で教えられている理由の誤解である。
2.後置記法による結果の計算。」(引用の終わり)
ただし、ステージ1を注意深く見てみましょう。 幸いなことに、著者はこのためのシックなテーブルを提供しています(p。153):
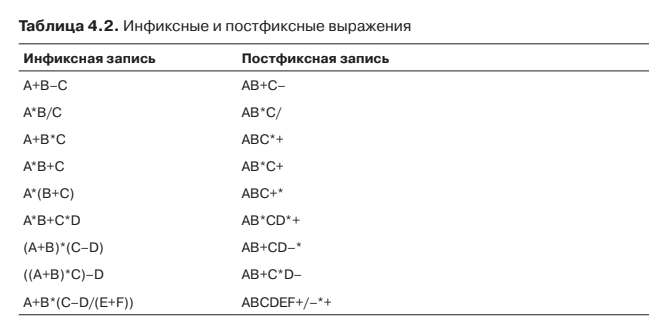
とりわけ、私は最後の行が好きでした。 神のために、ここからスタックから順番に引き出して、正しい結果を得る方法を教えてください。 オペランドと操作が別々の2つのスタックのシステムは引き続き機能しますが、1つのスタックで...
しかし、これはそれについてでさえありません。 インフィックス(私たちに馴染みのある)レコードからポストフィックスを作成するには、いくつのソートを行う必要がありますか? なぜ古代の方法のために学生の通常の人間の論理を破るのですか? たとえば、そのような式がどのように見えるか想像するのも怖いです:(A + B * C / D)+(EF *((G /(HJ *(-1)+ I)-L *(MN)-R)+ S )。そして、すぐに想像できましたか?
したがって、中置レコードから後置レコードへの変換には、ソースデータをソートするための複雑なあいまいなアルゴリズムの実装に、不当に高いコストがすでにかかっていると言えます。 さらに、この段階での返品数は、中置(通常)レコードの処理に必要なリソースを明らかに超えます。 さて、このような接尾辞レコード自体の処理は、何らかの形でスタックから行をプルするプリミティブに限定されず、適切なプロセッサと追加のリソースを必要とします。
必要な操作(OPN)のシーケンスを簡単な例で説明します。

表1 数式のフラグメントを計算する手順
しかし、これがすべてではありません。数字が複数の数字で構成されている場合、個々の数字をスタックまたは出力行に配置する前に、その数字を組み立てるためにバッファを配置する必要があるからです。
アレスターの計算方法を再評価するタスクはありません。そのため、特に興味のある人は、オリジナルのソースでそれについて読むことができます。 したがって、記事のタイトルで発表されたメソッド(アルゴリズム)のピンポンに目を向けます。
すぐに予約を行うと、数式を解析するための多くのメソッド(アルゴリズム)があります。 再帰的下降のメソッドと、ツリーなどを構築するメソッドに名前を付けることができます。 ネットワーク上でピンポンは見つかりませんでしたが、かなり頻繁に使用されていると思います。 彼がそのような名前を受け取った理由は、イラストから明らかになるでしょう。
そこで、アルゴリズムの分析に進みます。 プレゼンテーションを簡単にするための定義から始めましょう。
優先度-ある操作の優位性または他の操作に対するグループ化。 アルゴリズムは3つの優先順位を使用します。0-操作「±」。 1-操作 "* /%"; 2-括弧「()」でグループ化。 注:この記事では、関数とそれらの操作は考慮されていません。 関数は、操作の優先度に影響を与えない独立したレイヤーです。
フラグメントは、低レベルの計算に渡すことができる式の一部です。 つまり、フラグメントは、括弧で囲まれ、0番目と1番目のレベルの演算を含む式の一部であり、2つのオペランドとそれらの間の演算の符号を含む些細なフラグメントの両方です。
説明の便宜上、アレスタの計算に上記で提案したものと同じ式を使用します:(A + B * C / D)+(EF *((G /(HJ *(-1)+ I)-L *(MN )-R)+ S)* W)。 アルゴリズムの動作を説明するプロセスでより明確にするために、文字を数字に置き換えます。 行こう
入力に数式行があります。

オペランドは、操作記号を基準にして、一方が左側に、もう一方が右側に引き出されます。 フラグメント内の操作のシーケンスは、結果の置換を伴う処理シーケンスの優先順位によって直接保護されます。 単項および二項の「-」問題は、加算/減算ブロック内で解決されます。
ですから、ここでは多くの説明は必要ないと思います。 まあ、名前の由来も明らかです。 ご覧のとおり、クラスとしてのソートはありません。式の長さとネストされたグループの数に制限はありません。 すべてが簡単な検索と置換のレベルにあります。 文字列のフラグメントを生成しないようにするには、Stringの代わりにStringBuilder(java)を使用するだけで十分です。これにより、不要なエンティティを生成せずに文字列を変換できます。 しかし、最も重要なこと-これはすべて、単純で直感的な知覚のレベルで理解可能である。
アルゴリズムを比較するために、同じ表記でそれらを表します。
アレスタのアルゴリズムはWikiから取得されます

ピンポンアルゴリズム

したがって、ピンポンアルゴリズムは人間の知覚に可能な限り近いものであり、最小限のリソースしか必要としません。 また、最小限の文字分析と意思決定手順が必要であり、数値から数値を組み立てるためのバッファは必要ありません。
このような直感的なアルゴリズムはたくさんあると思います。 それでは、なぜ学生は太古の昔に発明されたあらゆる種類のがらくたに苦しめられているのでしょうか?
このアルゴリズムが誰かに役立つと嬉しいです。