データジオメトリ4.グラフ空間

点ベースの座標系の特徴（ 二および二座標 ）は、通常の幾何空間とグラフ空間の両方で使用できることです。

グラフ空間とは

空間の次元と基底の次元

グラフ空間の次元は、接続されている頂点の数によって決定されます（グラフのすべての頂点が接続されていることを前提としています-1成分グラフ）。 空間の基礎は、既知の距離（メトリック）を持つグラフの頂点のサブセットとして定義されます。 サブセットには、グラフのすべての頂点と一部（サブグラフ）の両方を含めることができます。 後者の場合、基底の次元はグラフの一般的な空間の次元よりも小さくなります。

グラフ空間の要素

グラフ上の要素とベクトルが何であるかを理解する必要があります。 グラフは、関連する要素（ノード）のコレクションです。 グラフのノードは潜在的な基本要素のセットを決定し、接続はメトリック、基本要素間の距離を決定します。



グラフ上の座標系を決定するための基礎として、グラフのすべてのノードを選択できるわけではなく、その一部、つまりベースサブグラフのみを選択できます。 この場合、グラフの一般的な空間は、基本と外部の基本（外部）の2つの部分空間に分割できます。



グラフの基礎に含まれるノードは、基本と呼ばれます。 空間の他のすべての要素は、重心座標（ベース頂点の重み）を介してそのベースノードに対して相対的に定義されます。



一般的な場合、要素は基底空間に属するか、基底空間の外側にあることができます。 基底外の要素は、 外部と呼ばれます 。 外部要素のベース空間までの距離はゼロではないため、各外部要素はその基底に含まれないグラフのノードです。 つまり、外部要素はグラフ構造で明示的に定義されます。



基底空間に属する要素は、構造内に一切表示されません。仮想要素（基底の明示的に指定された頂点を除く）。 仮想要素のノルムはゼロです。これは、基底の頂点で単一性に正規化された潜在的なベクトルです。 基底空間の仮想要素の例は、基底のオルソセンターです。



グラフが電気回路の場合、要素はネットワークのノードでの電位のセットです。 電気回路のラプラシアンは、リブの導電率で構成されるマトリックスです。 この行列にノードの電位を掛けると、ノード内の電流が得られます。 したがって、ノードのポテンシャルは距離座標です $$$u_i \ equiv dm_i$ 、および合計ノード電流は重心です： $$$i ^ j \ equiv bm ^ j$ 。 座標変換は、単にオームの法則を反映しています。



$$$L ^ {ji} u_i = i ^ j$



要素が物質的なものであり、それらのコンポーネントが仮想（重み、距離、投影）である通常の空間認識とは異なり、グラフ空間では状況は反対です。 要素のコンポーネント（ノード内の電位と電流）は重要であり、空間内の要素の位置は仮想であり、コンポーネントの値のセットによって決定されます。

グラフ上の座標系の構築

問題の声明

グラフ上の座標系（SC）を構築するタスクは、次のように定式化できます。

1. グラフは、相互接続された頂点のセットとして与えられます。
2. グラフのすべての頂点のセットから、 基底 （メトリックテンソルを構築できる頂点のセット）が選択されます-距離またはラプラス。
3. グラフの残りの頂点は外部です。 外部頂点の場合：
   
   
   • 頂点の一般的な接続性（その接続の重みの合計）。
   • 頂点間の接続。
   • 外部頂点と基底の頂点との関係。

基底に関して外側の頂点の座標を決定する必要があります。 座標系では、グラフのすべての（任意の）頂点間の距離を決定できる必要があります。



SCを構築する問題の可能な定式化の1つだけが与えられていることを明確にしましょう。 既知のパラメータと決定する必要があるパラメータの組み合わせは異なる場合があります。

基本サブグラフ

グラフのベース頂点のセットをインデックスで示します $$$a$ （anchor-anchor）、およびインデックスによる他の頂点のセット $$$t$ 。 これらのセットを組み合わせると、グラフのすべての頂点が得られます。 グラフのノードは、少なくとも1つの接続によって他のノードと接続されていると見なします。



グラフの一般距離計量テンソル（DMT） $$$Gm$ 4つのマトリックスに分割できます。



$$$Gm = \ begin {pmatrix} Gm_ {aa}＆Dm_ {at} \\ Dm_ {ta}＆G_ {tt} \ end {pmatrix} \ quad（4.1.1）$



$$$Gm_ {aa}$ -サブグラフの距離計量テンソル。



$$$Dm_ {at}$ -外部頂点の二座標のマトリックス $$$t$ 基本的に $$$a$ 。 このマトリックスでは、頂点座標は転置されたマトリックスの列です。 $$$Dm_ {ta}$ 文字列です。



$$$G_ {tt}$ -基底に含まれないグラフの頂点間のスカラー積の行列。



問題の条件により、部分グラフのグラミアンのみが知られています。 $$$Gm_ {aa}$ 。 行列 $$$Dm_ {at}$ そして $$$G_ {tt}$ -これは、グラフの構造に関するデータに基づいて決定する必要があるものです。

ラプラシアン構造

同様に（4つの部分行列に）、グラフのラプラシアンを分割できます。 $$$L$ 。 グラミアンとは対照的に、グラフのラプラシアンはここではマイナーです-グラフのオルソセンターに関するデータはありません。



$$$L = \ begin {pmatrix} L ^ {aa}＆-C ^ {at} \\ -C ^ {ta}＆L ^ {tt} \ end {pmatrix} \ quad（4.1.2）$



$$$C ^ {at} =-L ^ {at}$ -グラフの外側の頂点間の接続（隣接）のマトリックス $$$t$ そしてその基礎 $$$a$ 。



$$$L ^ {tt}$ -マイナーラプラシアン、外側のピークの接続。 このマトリックスの対角線上にあるのは、ノードの総伝導率（エッジの総重量）の値であり、残りの要素はノード間の接続の大きさです。 通常、このマトリックスは可逆です。 その逆は基本行列と呼ばれます：



$$$F_ {tt} = / L ^ {tt} \ quad（4.2）$



「基本」という用語は、吸収を伴うマルコフ連鎖の理論から取られています。 このようなチェーンでは、ベースノードの役割は、リターン（吸収）のないノードによって果たされます。 このマトリックスの使用例は、指定されたオブジェクトからの遠隔性の程度によってオブジェクトをランク付けする方法に関する記事で提供されました 。



行列の1つ（ラプラシアンマイナー $$$L ^ {tt}$ または基本行列 $$$F_ {tt}$ ）知られています。 （4.2）によると、他の1つを表現できます。

基本的なアイデンティティ

グラミアンとラプラシアンのカウントは互いに逆です。



$$$Gm \ cdot Lm = I \ quad（4.3）$



上記の行列をつなぐ恒等式を見つけるには、ブロック行列（4.1.1）と（4.1.2）を（4.3）に置き換える必要があります（事前にラプラシアンをオルソセンター条件付きパラメーターで境界付けます）。 その結果、次の関係が得られます。

ラプラス接続 $$$Lm ^ {aa}$ そしてリモート $$$Gm_ {aa}$ サブグラフの基底の計量テンソル：



$$$Lm ^ {aa} Gm_ {aa} = I ^ {a} _ {a} \ quad（4.4.1）$



（4.4.1）1つのテンソルを別のテンソルに基づいて計算できます。 基底が関係の形で与えられる場合、基底のラプラシアンを決定する $$$La$ 次のIDを使用できます。



$$$La = L ^ {aa}-B ^ {a} _ {t} C ^ {ta} = L ^ {aa}-C ^ {at} F_ {tt} C ^ {ta} \ quad（4.4.2 ）$



ここに $$$L ^ {aa}$ -ベース頂点の元のラプラシアンのマイナー。 $$$La$ -ラプラシアン、LMT基底の部分行列。 このラプラシアンに基づいて、サブグラフのグラミアンを見つけることができます $$$Gm_ {aa}$ 。



グラフの外部ノードとその基底間の接続のマトリックスがわかっている場合 $$$C ^ {at}$ 基本行列と同様に $$$F_ {tt}$ 、ノードの重心座標を計算することが可能です：



$$$B ^ {a} _ {t} = C ^ {at} F_ {tt} \ quad（4.4.3）$



重心座標のマトリックス $$$B ^ {a} _ {t}$ 影響マトリックスとも呼ばれます。 実際、その値は、残りのベース頂点の影響を反映しています（ディリクレ問題では、外部ノードの境界ノードの値の影響）。



ノードの2座標と2座標は相互に関係しています。 計量基底テンソルにより表現されます：



$$$Dm_ {at} = Gm_ {aa} Bm ^ {a} _ {t}、\ quad Bm ^ {a} _ {t} = Lm ^ {aa} Dm_ {at} \ quad（4.4.4）$



二座標には、単位と、基底をもつ要素のスカラー積の値が含まれます。 $$$Dm_ {ta} = [1_t; D_ {ta}]$ 。

双座標は、スカラー成分（軌道）と重心座標で構成されます。

$$$Bm ^ {a} _ {t} = [W_t; B ^ {a} _ {t}]$



基本行列とLMT基底の行列式がわかっている場合、グラフのラプラシアンの総スカラーポテンシャルを計算できます。



$$$u（L）= -Det（Lm ^ {aa}）/ Det（F_ {tt}）\ quad（4.4.5）$



外部頂点のスカラー積の行列 $$$G ^ a_ {tt}$ サブグラフに基づいて $$$a$ は、頂点の2座標または2座標で表される双一次形式を表します。



$$$G ^ a_ {tt} = Dm_ {ta} Lm ^ {aa} Dm_ {at} = Bm_ {t} ^ {a} Gm_ {aa} Bm ^ {a} _ {t} \ quad（4.4.6）$

基本行列と頂点間の距離

明らかに、行列の値 $$$G ^ a_ {tt}$ 通常、元のグラフの頂点のスカラー積の値とは異なります $$$G_ {tt}$ 。 それらの違いは、基本的なマトリックスで表されます。



$$$G_ {tt}-G ^ a_ {tt} = F_ {tt} \ quad（4.5）$



式（4.5）を使用して、頂点（要素）間の真のスカラー積を計算できます。 $$$G_ {tt}$ 部分グラフの基底の要素のスカラー積が既知の場合 $$$G ^ a_ {tt}$ および基本行列 $$$F_ {tt}$ 。



元のグラフでは、頂点のノルムはゼロです。 したがって、スカラー積 $$$G_ {tt}$ 頂点間の距離の二乗で表現できます $$$Q_ {tt}$ ： $$$G_ {tt} = -Q_ {tt} / 2$ 。 （4.5）は次のように表すことができます。



$$$F_ {tt} + G ^ a_ {tt} + Q_ {tt} / 2 = 0 \ quad（4.5.1）$



要素のスカラー積- （2.6）を決定するときに、2番目の部分でこの式にすでに遭遇しています。 式を比較すると、基本行列の値は、基底に対する頂点のスカラー積によって表現できることがわかります。



$$$F_ {ij} = G_ {ii '、jj'} = G_ {ij、a} =-（Q_ {ij} + Q_ {i'j '}-Q_ {ij'}-Q_ {i'j}） / 2 \クワッド（4.6.1）$



ダッシュは、ベーススペース上の頂点の投影を示します。 $$$G_ {ii '、jj'}$ ペアのスカラー積です $$$（i、i '）$ そして $$$（j、j '）$ 。

を通して $$$G_ {ij、a}$ は、頂点の法線のスカラー積を示します $$$i、j$ 宇宙へ $$$a$ 。



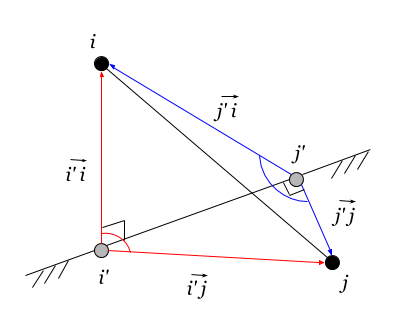
法線は、基本空間での要素からその投影への方向として定義されます。 これは、原点ではなく、通常の座標系の要素の座標のスカラー積を（ベクトルベースで）決定することに近く、ここでは空間が示されています。



頂点のいずれかがベース空間に属している場合、他の頂点との基底に対するスカラー積はゼロに等しくなります。 したがって、基本行列の要素の1つがゼロに等しい場合、行列の行と列全体もゼロになります。



アイテムが $$$i$ そして $$$j$ 一致する場合、基本行列の値は、要素からベース空間までの距離に等しいか、（2.5）要素の負のノルムに従っています。



$$$F_ {ii} = -N_ {i} \ quad（4.6.2）$ -基本行列の対角要素の値。

基本空間外の要素間の距離

頂点が（スーパースペースに属する）ベーススペースに属していない場合、次の2つの状況が考えられます。



1.頂点は同じ（上記の）スペースに属します。 この場合、頂点とベース空間上の投影は同じ平面にあります。

2.頂点は異なる（上記の）スペースに属します（上の図に示されています）。



最初の状況では、法線の方向 $$$\ vec {ai}$ そして $$$\ vec {aj}$ 共線であるため、スカラー積は頂点からベース空間までの距離の積と一致します。



$$$F_ {ij} = \ sqrt {N_ {i} N_ {j}} \ quad（4.6.3）$



頂点が空間の片側にある場合（法線は一方向に向けられている）、平方根の符号は正であり、反対の場合は負です。 この式は、シリーズの第2回の記事（2.7）で既に提供されています。 式（4.6.3）は、特定の（重要ではあるが）ケースを説明しています。

軌道の行列

座標系を構築するには、双座標のスカラー成分（ 要素の軌道と呼ばれるもの）を決定する必要があります 。 このコンポーネントがないと、グラフ内の距離はベース空間のフレームワーク内でのみ取得できます。



双座標の決定のために、要素の軌道と基底空間への投影を要素のノルムに関連付ける式が得られました-（2.9.1）：



$$$W_ {t} = W_ {t '} + N_ {t} / 2 \ quad（4.7）$



要素の射影軌道は双線形形式（2.9.2）で計算できます。これは基底グラミアンとして知られているためです。 $$$G_ {aa}$ 、および要素の重心座標（4.4.3）。 （4.6.2）による要素のノルムの値は、基本行列の対角要素から取得できます。 すべてをまとめると、相互軌道の行列の式が得られます。



$$$W_ {tt} =-（B_ {t} ^ {a} \ G_ {aa} \ B ^ {a} _ {t} + F_ {tt}）/ 2 \ quad（4.8）$



この行列の対角値 $$$Diag（W_ {tt}）$ ピークの軌道です。



したがって、外側の頂点の双座標が決定されます。 双座標に基づいて、式（4.4.4）に従って二座標を計算し、相互ノルム（4.4.2）のマトリックスを取得できます。



座標系を構築するタスクが完了しました。

浅いベース

基底に少数の頂点が含まれている場合、反転式（4.4）の一部を明示的な形式で表現できます。 ここでは、1つと2つの頂点のベースを検討します。

シングルピークベース

これは非常に簡単なため、あまり面白くありません。 距離計量基底テンソルには、単一の距離は含まれません。



$$$Gm = \ begin {pmatrix} 0＆1 \\ 1＆0 \ end {pmatrix}$



基底を基準とした頂点の重心座標はすべて1に等しくなります（コンポーネントが1つしかないため）。 基本行列は、ペアのスカラー積の行列と一致します。各ペアの最初の要素は基底の最上部にすぎません。 第3部では、このような行列に基づく距離行列が距離変換によって取得できることが示されました。



$$$Q_ {ij} = F_ {ii} + F_ {jj}-2F_ {ij}$

2つのピークの基礎

このような基盤は実際的に重要です。 たとえば、以前に検討された電気測定の問題では、外部電圧が印加されるノードは2頂点ベースです。



ベース頂点間の距離を示します $$$A$ そして $$$B$ どうやって $$$r = q_ {AB}$ 。 電気回路では、距離はノード間の抵抗に等しいことを思い出してください。 距離計量基底テンソルの形式は次のとおりです。



$$$Gm = \ begin {pmatrix} 0＆1＆1 \\ 1＆0＆-r / 2 \\ 1＆-r / 2＆0 \ end {pmatrix} \ quad（4.9）$



DMTの決定要因： $$$Det（Gm）=-r$ 。 ラプラステンソル（LMT）は、リモート（4.4.1）を逆にすることによって取得されます。



$$$Lm = \ begin {pmatrix} r / 4＆0.5＆0.5 \\ 0.5＆/ r＆-/ r \\ 0.5＆-/ r＆/ r \ end {pmatrix} \ quad（4.10）$



グラフの頂点の2座標には3つのコンポーネントがあります。スカラー（1）、スカラー積 $$$d_A$ ベース頂点に相対的 $$$A$ およびスカラー積 $$$d_B$ ベース頂点に相対的 $$$B$ ：



$$$Dm = [1; d_A、d_B] \ quad（4.11.1）$



Bi座標にも3つのコンポーネントがあります。 スカラー成分は、頂点の（幾何学的）軌道です。



$$$Bm = [w; B] = [w; b_A、b_B] \ quad（4.11.2）$



（4.11.1）を（4.4.5）に代入し、（3.8）を考慮して、頂点Pの 2座標成分の式を取得します。



$$$Bm_P = [-g ^ P_ {AB} / 2; g ^ B_ {AP} / r、g ^ A_ {BP} / r] \ quad（4.12）$



ここで $$$g ^ Z_ {XY} = g_ {ZX、ZY}$ 始まりが最上部にあるペアのスカラー積 $$$Z$ 要素で終わる $$$X$ そして $$$Y$ 。



$$$g ^ Z_ {XY} = d_ {XY}-d_ {XZ}-d_ {YZ} \ quad（4.13）$



次のように、重心成分の合計が1であることを確認できます。 $$$b_A + b_B = 1$ 。

2頂点ベースのグラフの電位差

（4.12）の座標の重心部分は影響のマトリックスであり 、外部頂点へのベース頂点の影響を伝えます。 たとえば、潜在的な値がベース頂点で与えられる場合 $$$U_a$ 、その後、残りの頂点のポテンシャル $$$U_t$ 影響マトリックスによる与えられたポテンシャルの積によって決定されます：



$$$U_P = B ^ {a} _ {P} U_a \ quad（4.14）$



与えられたポテンシャルのベクトルを次の形式にします $$$U_a = [U_A、0]$ 。 そうすると、グラフの要素PとQの間の電位差は次のようになります。



$$U P - U Q = （B P A - B Q A）U A = g A B 、 P Q U A / r = g A B 、 P Q J q u a d （ 4.15 ） 導出では、アイデンティティ（3.9。 4）隣接するペアのスカラー積の差。$U_P-U_Q =（B_ {PA}-B_ {QA}）U_A = g_ {AB、PQ} U_A / r = g_ {AB、PQ} J \ quad（4.15）$



$$Jは、次の方程式によって決定される入力ストリームの値です。$J$$$$La \ U_a = J$ 。



式（4.15）は、前の記事で示したように、グラフの頂点での電位差とスカラー積との関係を明示的に表しています。

---

まとめると。このパートでは、グラフに座標系を設定する方法を示します。基本的なアイデンティティが与えられており、私たちの意見ではそのキーは（4.5）と（4.5.1）です。

必須プログラムからは、座標変換（基本変更）を検討する必要があります。これは次の記事で行います。