多くの場合、実際には、研究対象のシステム（黒点、年平均降水量から金融市場、経済指標の時系列）は通常分布していないか、それに近いものではありません。 そのようなシステムを分析するために、ハースト[1]は正規化スパンの方法（RS分析）を提案しました。 この方法により、主にランダムな時系列とフラクタル時系列を区別し、非周期的なサイクル、長期記憶などの存在について結論を出すことができます。
RS分析アルゴリズム
- 元の行が与えられます
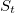。 対数関係を計算します。
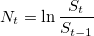
- 行を分割する
に 
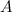連続した期間が長い 
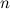。 各期間にマークを付ける 
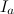どこで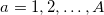 
。 それぞれに定義します 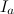平均値：
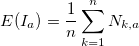
- 各期間の平均値からの偏差を計算します ：
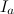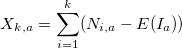
- 各期間内の範囲を計算します。
- 各期間の標準偏差を計算します。 ：
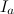- 毎
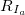割る 
。 次に、 R / Sの平均値を計算します。
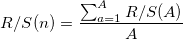
- 増やす 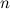そして、手順2〜6を繰り返します
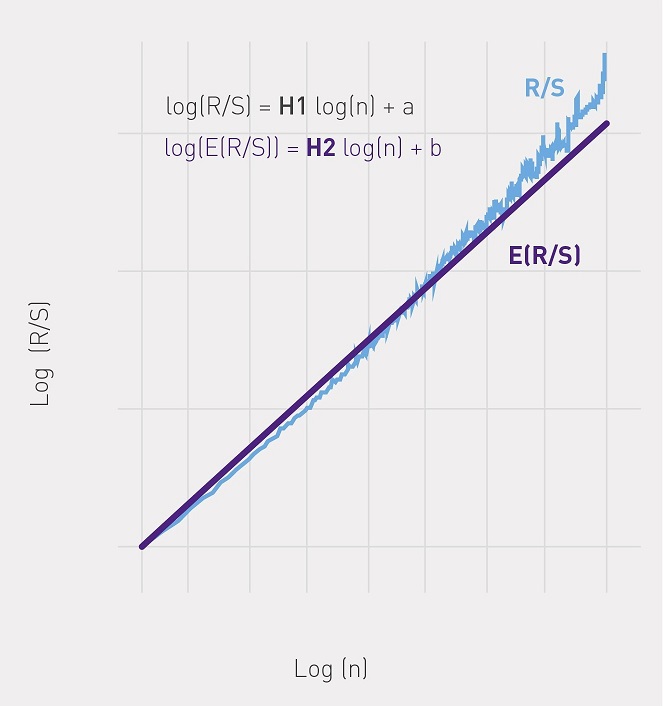
- 依存関係グラフを作成する
から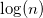 
そして、最小二乗法を使用して、次の形式の回帰を見つけます。 
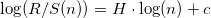、ここでHはハースト指数です（図を参照）。
有意性チェック
次に、有意性の結果を確認します。 これを行うには、分析された構造が正規分布しているという仮説をテストします。 R / Sはランダム変数であり、正規分布しているため、 Hも正規分布していると仮定できます。 独立したプロセスの漸近的な制限は、0.5のハースト指数です。 エニスとロイド[2]、およびピーターズ[3]は、次の予想されるR / Sインジケータの使用を提案しました。
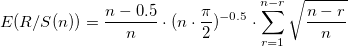
n個の観測値について、予想されるハーストパラメーターを見つけます。
。
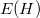予想される分散は次のとおりです。
ここで、 Tはサンプル内の観測値の数です。
選択した統計：
。
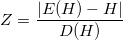それを正規化された正規分布の臨界値と比較します。
サンプル値がクリティカル未満の場合 、システムの正規分布の仮説はこの有意水準では拒否されません 。 構造はランダムであり、正規分布の法則があります。
参照：
- Hurst、G. E.、1951。「長期貯水池容量」。 アメリカ土木学会論文集、116、770-808。
- Anis、AA、Lloyd、EH（1976）独立した通常の加数の調整された再スケーリングされたハースト範囲の期待値。 Biometrica 63：283-298。
- ピーターズ、EE（1994）フラクタル市場分析。 ワイリー、ニューヨーク。 ISBN 0-471-58524-6。