The most comprehensive classification of underwater navigation systems that you can find

Greetings, dear ones!

"Hydroacoustics - the corrupt girl of imperialism!" (C)

Why is underwater navigation important? Yes, because without it, any underwater vehicle is an expensive toy that is not known where, because it is easier and cheaper to make thousands of the same type of underwater robots, and in order to destroy a submarine with dozens of trained crew, one of them is enough.



So what? Long, short, ultra short? Oh no, everything is much deeper! The devil, as usual, lies in the implementation. How the underwater navigation systems are arranged in the real world, why they are arranged exactly the way they work - today I will put it all on the shelves.

With trace amounts of matan as spices, of course.



The bonus is an open source library for solving navigation problems.



Who is not afraid - welcome to the cool December waters of our pond!







So, the last time I, paying tribute to the established order, said that:

• there are long, short and ultrashort-base systems;
• why long is always better and what are the advantages and disadvantages of these types of systems;
• the base line is formed by two points with a known position, from which either angles or ranges or pseudorange to the desired point are measured.

Here on this foundation of knowledge I propose and continue.



As you can see, the existing well-established classification speaks only about the composition of the system and only to some extent about the principles of functioning, leaving a concrete implementation behind the brackets.





For example, a long-range system can be arranged with both range measurements and pseudorange measurements, in the latter case if the base is active, i.e. radiating, then with its support an unlimited number of simultaneously positioned receivers can work, with the generation of coordinates on positioned objects (navigation system). So, for example, global satellite systems work - GPS, GLONASS, Gallileo, Beidou (as well as our “Underwater GPS” ).



All mentioned systems are systems on a long base. But, for example, in a parallel universe there would be the same systems, but operating not according to the differential-ranging, but according to the ranging method, then in order to get your position on the map, you would need to send a request for satellites (for humane reasons, suppose that they all have a common request), accept at least 4 responses, using the double signal propagation time and the fixed delay in processing the request signal on the satellite, calculate the distances to each satellite and solve the navigation problem.



Enchanting inconvenience of such an organization is difficult to overestimate. But let me remind you, from the point of view of modern terminology - both that and another - long-base systems.



Another option - if the object radiates, that is, the ability to "follow" it - remotely determine its coordinates (positioning system).



For example, an ultrashort-base system (UKB) system can request a beacon-transponder or determine the distance to a pinger by prior synchronization or with a request using an electric or optical channel. In all these cases, these will be ultrashort-base systems.



Naturally, the use of a particular scheme and / or layout has various limitations and advantages, therefore it is important to have a more complete classification.



We begin to introduce classification features.

By the method of measuring propagation time

This symptom is the most basic, because regardless of the type of system, its configuration and specific performance, everything works precisely on measuring the propagation time of a signal.

So, how can you measure the propagation time of a signal between two devices?

Request-response method

The simplest and most obvious approach is to use the so-called request-response method. Its essence is as follows.



Let the requesting system emit a request signal at a time $$$t_R$ , which she captures by her internal clock. In an optimistic case, the requested system receives this signal at some point in time $$$t_ {A1}$ , which it captures by its clock that is not synchronized with the clock of the requested system. Since in reality navigation signals have a certain duration and the system leading them always makes a decision on successful reception with some delay, which is also not necessarily constant, some fixed response delay is required $$$t_d$ known to both the requested and the requesting systems.

This position is shown in the figure below:





Timing diagram for determining the propagation time of a signal by the request-response method



In the following figure, the situation with the delay of the decision to detect the signal is considered in more detail:





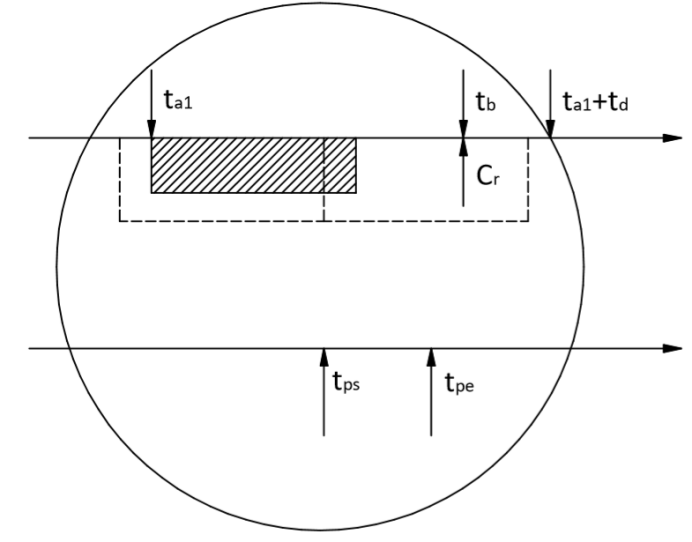
Signal analysis lag. The dashed lines show the duration of the processing windows, the shaded areas represent the useful signal in the ring buffer.



The actual start of the analysis of the window that contains the useful signal occurs after the entire signal is in the ring buffer, the analysis lasts from the point in time $$$t_ {ps}$ before $$$t_ {pe}$ , and during this time the ring buffer is replenished. Thus, to ensure the continuity of the timeline, it is necessary that the response to the request is made after a fixed time from the moment the signal is received, obviously longer than the duration of the window and the duration of its processing.



Now, the requested system after successfully receiving and calculating the actual time of arrival of the signal $$$t_ {A1}$ should emit a response signal at some point in time $$$t_ {R1} = t_ {A1} + t_d$ . The requesting system, in turn, in the same way receives a response signal at a time $$$t_A$ , and can now calculate the propagation time $$$t_F$ signal in a trivial way:

$$

$$t_F = (t_A-t_R-t_d) / 2$$

Here we make the assumption that throughout the transaction the distance between the requesting and requested systems remains either constant or its change is not essential within the framework of the problem being solved.



The determination of the propagation time in this way is widely used in UKB systems, systems with a virtual long base, long base, and some others.



The advantages of this method include:

• no time synchronization of the requesting and requested systems is required (and accordingly, very precise hours are not required);
• the possibility of implementing an address request when the request signal contains information that uniquely determines its belonging to a particular subscriber;
• the ability to apply different queries in a digital system - separately request different parameters. For example, if we are talking about a moving object, then it is logical to request its depth more often and less often the temperature and battery charge, etc.
• simplicity and reliability of implementation;

Cons of this method:

• measurement requires two successful techniques - on the requested and on the requesting system;
• and the requested and requesting systems should contain both receiving and transmitting paths;
• it is necessary to implement the mechanism of waiting and processing the excess of the waiting interval (timeout processing);
• work with several requested systems can only be implemented alternately
  
  
  In fact...

  In fact, there existed (and, possibly, are still used today) systems with tonal beacons-responders, which had the same set of tonal premises as a request signal and different sets as response (which allowed them to be identified) signals. A narrow signal band allowed to request several such beacons at once. It is obvious, however, that today such systems can hardly be considered to meet the challenges of the times;
  
  

Semi-acoustic method: a variation of the request-response method with a request via an electric or optical channel

In a number of tasks where it is possible to communicate over the radio channel or even over the wire between the requesting and requesting systems (which is often the case, for example, in the case of genetically modified divers of TNLA), the task can be greatly simplified by applying a gating pulse instead of the request signal.



In this case:

• firstly, the time of the entire transaction is significantly reduced due to the duration of the request signal and its propagation to the requested system (it is not necessary to send a super-stable broadband signal via cable - a simple rectangular pulse is enough);
• secondly, the fixed delay time, in turn, can also be significantly reduced,
• and thirdly, now the requested system should no longer contain a sufficiently algorithmically complex receiver;
• fourthly, the errors associated with signal propagation in the medium immediately decrease by half.

The propagation time for this variation of the method will be calculated even easier:

$$

$$t_F = t_A-t_r-t_d$$

Where $$$t_A$ - the time of receipt of the response signal on the requesting system, $$$t_r$ - the time of formation of the strobe pulse, $$$t_d$ - fixed delay.



Obviously, not only the request half of the distance can be overcome not by the acoustic channel, but also the response.

Distributed receiver request-response (combined)

This variation of the method relates to long- and short-range navigation systems. Imagine that the requesting system contains one transmitter and several receivers, the clocks on all receivers are synchronized and their positions are known (it is especially easy to imagine such a system if these several receivers are floating buoys, each of which has a GNSS receiver that generates a geographic location and provides quite accurate time strobe - 1PPS pulse ).



Now, by analogy with the usual request-response method, the propagation time $$$t_ {F1}$ before the transmitter is determined:

$$

$$t_ {F1} = (t_ {A1} -t_ {r1} -t_d) / 2$$

Where $$$t_ {A1}$ and $$$t_ {r1}$ - the arrival time of the response signal and the emission time of the request signal of the transmitter, respectively, $$$t_d$ - fixed response delay.



The following figure provides an explanation of the described scheme:





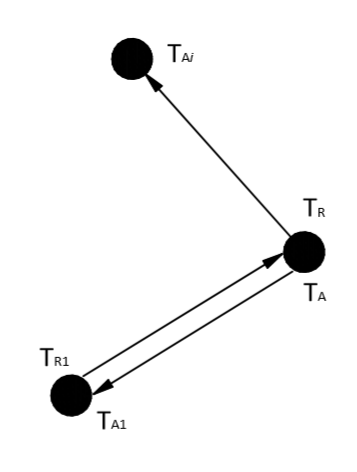
Determination of propagation time to all elements of a distributed receiver



And the time of distribution $$$t_ {Fi}$ to the i-th receiver will be respectively:

$$

$$t_ {Fi} = t_ {Ai} -t_ {r1} -t_d-t_ {F1}$$

or

$$

$$t_ {Fi} = t_ {Ai} - (t_ {r1} + t_d + t_ {A1}) / 2$$

Where $$$t_ {Ai}$ - time of arrival of the signal from the requested system to the i- th receiver.



That is, after the transaction is completed, there is a set of points with known coordinates and ranges to them, which in fact is already very close to the long-range navigation system.

Pre-sync

Or, as it is sometimes called - a one-way measurement of the propagation time, it is used when either one of the interacting systems cannot for some reason emit a signal (for example, it tries to mask itself more acoustically!) Or when the propagation time is too long.



It is understood that at some point in time, the clocks of all the interacting systems were synchronized.



In the context of this method, it is no longer completely incorrect to use the terms “requesting” and “requested” system, so for simplicity we will use the familiar “transmitter” and “receiver”.



In fact, when implementing this method, two approaches can take place:



- In the first, there is only one transmitter that emits a navigation signal at regular intervals $$$t_p$ . At some point in time $$$t_s$ , according to the clock of the receiver, the clock of the receiver and transmitter are synchronized. After this, the propagation time from the transmitter to the receiver can be determined by a simple relation:

$$

$$t_F = (t_A-t_s) mod (t_p)$$

Here $$$t_A$ - time of signal arrival to the receiver.



If you carefully look at this ratio, you can see that using it you can not measure the propagation time greater than $$$t_p$ .

Along with such a serious drawback of the above approach, it has one extremely strong plus: in this way the so-called drive to a lighthouse (transmitter) of a theoretically unlimited number of receivers: imagine that a receiver synchronized at some point has an antenna array, determines the distance to the drive beacon and the horizontal angle of signal arrival.



Which is very convenient, for example, when solving the problem of driving divers - they can go from the place of discharge to tangible distances, and in the case of surfacing a few hundred meters from the point of discharge, to float on the surface with balloons is an activity so-so.



So this approach is implemented, for example, in our Vostok divers drive system.



- The second approach does not impose any restrictions on the number of transmitters and practically does not require periodic signal emission. It still appears in the clock synchronization time of the receiver and transmitter $$$t_s$ , and the actual radiation time $$$t_r$ explicitly contained in the transmitted message. On the receiver side, signal propagation time $$$t_F$ defined as:

$$

$$t_F = t_A-t_r-t_s$$

Without going deep into details, we note that the minus of the circuit with preliminary synchronization is exactly one - the clocks of different devices quickly diverge to unacceptable values.



To give a quantitative sense of how quickly this happens, I will say that with the use of thermostabilized quartz resonators, a difference of 7 milliseconds accumulates on average in 1.5-2 hours.



Taking into account the average value of the speed of sound in water (~ 1500 m / s), this discrepancy leads to an error in determining the distance of ~ 10 meters.



Recently, by the way, colleagues report the successful use of miniaturized atomic clocks (!), In which the indicated accuracy lasts for weeks [1] [2].



In addition to the methods with pre-synchronization, mention may be made of schemes where primary synchronization is provided by the request-response method.



For example, a request initiates a series of response signals, the period of which is $$$t_p$ . The first response signal allows you to determine the propagation time of the signal $$$t_ {psyn}$ at the time of synchronization.



The clock of the requesting system at the time of the first response signal $$$t_ {syn}$ .

Now, to calculate the propagation time $$$t_F$ for each of the subsequent response signals, you can use a simple formula:

$$

$$t_F = t_ {psyn} + t_Amod (t_p) -t_ {syn}$$

Where, $$$t_A$ - time of arrival of the next response signal according to the hours of the requesting system.



Such a scheme has a certain flexibility: the number of responses can be explicitly indicated in the first request signal, and the scheme itself allows several subscribers to work with time division.



At the same time, this approach introduces a certain amount of ambiguity - if the requesting system skips receiving the first response signal, then the work stops until the completion of the entire cycle of transmission of response signals. And in addition to the error associated with the departure of the watch, an error is added to the initial synchronization. In most existing systems, the error in determining the oblique range is indicated in the range from 1% to 0.1% of the actual oblique range. Those. in the average case, the error of the initial synchronization at distances of the order of 1000 meters can be about 10 meters due to the nonlinearity of the propagation of sound waves in the hydroacoustic channel, without taking into account the errors associated with the determination of the direct beam (the mythical “direct signal”, and not one of copies of it, reflected from something).



Okay, they seem to have figured out different methods of measuring the propagation time of a signal, but this is clearly not enough. How else are navigation systems different? Surprisingly:

By a set of measured parameters

This criterion classifies systems according to a set of measured parameters; its main task is to distinguish between goniometric systems from rangefinder and differencefarget. And especially take into account the fact that some systems can work both as goniometric and as ranging (for example, some KB systems and DB systems when a positioned object leaves the navigation base).

Goniometer-distance measuring systems

This type of system determines the position of the positioned object in the polar coordinate system and is characterized by the following sets of measured parameters:

• Type I: $$$\ lambda_0, \ phi_0, z_0, \ alpha, e, t_F$
• Type I: $$$\ lambda_0, \ phi_0, z_0, \ alpha, z_s, t_F$

Where $$$\ lambda_0, \ phi_0, z_0$ - coordinates of the reference point (longitude, latitude, depth), $$$\ alpha$ and $$$e$ - horizontal and vertical angles of arrival of the signal, respectively, $$$z_s$ - the vertical coordinate (depth, distance from the water surface) of the positioned object, and $$$t_F$ - the propagation time of the signal between the reference point and the positioned object.



As shown above, the propagation time can be determined in each of two types according to three general principles:

• a) by request-response method:
  
  $$$t_F = (t_A-t_R-t_d) / 2$
• b) foreplay synchronization:
  
  $$$t_F = (t_A-t_S) mod (t_p)$ or
  
  $$$t_F = t_ {psyn} + t_Amod (t_p) -t_ {syn}$
• c) semi-acoustic:
  
  $$$t_F = t_A-t_R-t_d$

Note that the angles $$$\ alpha$ and $$$e$ for simplicity, they are calculated in the global coordinate system (i.e., they are counted from the true north direction clockwise and from the horizontal down, respectively).



For a long time, I doubted whether it would be worth adding large formulas to the article. Ultimately, those who simply feel idle curiosity may not be able to open the spoiler, and some student whom this really helps will be saved. No extra paragraph is worth the tear of a student!



In general, the problem of determining the angles of arrival of a signal can be formalized as follows:





The navigation problem in such systems is solved in two stages:

1. Projection definition $$r p slant range r to the surface of the water (range in plan);$r_p$
2. The solution of the direct geodesic problem - finding the position of the desired point in the directional angle and distance; namely$$$\lambda_s,\phi_s,z_s$ ;

For type I, the definition of the projection $$r p oblique range and depth$r_p$$$z s of the desired object are determined from the trivial trigonometric relations:$z_s$

$$

$$\begin{matrix} r_p=r*\cos e\\ z_s=r*\sin e \end{matrix}$$

Where r is determined even more trivially from the propagation time $$t F and sound velocity$t_F$$$$\nu$ ;

Determining the position of the desired object - coordinates $$λ s , ϕ s are obtained as a solution to the direct geodesic problem on an ellipsoid. Computationally efficient solutions that provide maximum accuracy are known from the works of Sodano [3] and Vincenti [4], and are commonly referred to as Vincenti Formulas in the common people. Here, forform's sakeof simplicity I will bring a simple solution for a sphere, giving the discrepancy in the distance to several kilometers, not exceeding 0.5 meters:$\lambda_s,\phi_s$

$$

$$\begin{matrix} \phi_s=\arcsin(\sin\phi_1*\cos\delta+\cos\phi_1*\sin\delta*\cos\alpha)\\ \lambda_s=\lambda_1+\arctan(\frac{\sin\alpha*\sin\delta*\cos\phi_1}{\cos\delta-\sin\phi_1*\sin\phi_s}) \end{matrix}$$

Where $$$\delta=r_p/R_E$ , but $$R E is the standard value of the earth's radius [5]. In the given dependence, all values ​​of angles in radians. To translate longitude$R_E$



$$λ s of the desired object in the familiar form ± 0..180 ° should use the simple formula:$\lambda_s$

$$

$$\lambda_s=(540+\lambda_s*180/\pi)mod360-180$$

In Some examples of systems operating on Type Ia this and here is this .

Type IIa systems are our Zima and TriTech MicronNav . At the same time, they say that MicronNav can also work in mode as a type IIc system.



As systems operating according to type IIb, we can cite our Vostok diving drive , and also in [1,2] it is reported about the use of miniature atomic clocks to ensure long-term synchronization in EvoLogics.de systems .

Rangefinder systems

Rangefinder systems can be divided into two types of systems, the difference between which is the availability of information about the vertical coordinate of the desired object or its absence.

• Type I: $$$\{x_1..x_n\}, \{y_1..y_n\},\{z_1..z_n\},\{t_{F1}..t_{Fn}\}$
• II: $$$\{x_1..x_n\}, \{y_1..y_n\},\{z_1..z_n\},z_s,\{t_{F1}..t_{Fn}\}$

Where n is the number of control points, the minimum value for n = 3, $${ x 1 . . x n } , { y 1 . . y n } , { z 1 . . z n } - coordinates of reference points;$\{x_1..x_n\}, \{y_1..y_n\},\{z_1..z_n\}$$${ t F 1 . . t F n } are the propagation times of the signal between the desired object and reference points;$\{t_{F1}..t_{Fn}\}$$$z s is the depth of the desired object. Often this type of task is incorrectly called TOA (English Time-of-arrival - time of arrival), which is more suitable for tasks solved in difference-distance-measuring systems TDOA (English Time-Difference-On-Arrival - difference in time of arrival), in while the more correct name is TOF (eng. Time-of-flight - travel time, distribution time). There are four methods for measuring propagation times for both types of systems:$z_s$

• a) by request-response method:
  
  $$$t_{Fi}=(t_{Ai}-t_{Ri}-t_d)/2$
• b) by pre-synchronization:
  
  $$$t_{Fi}=(t_{Ai}-t_s)mod(t_p)$
• ) «»:
  
  $$$t_{Fi}=t_{Ai}-t_R-t_d$
• d) :
  
  $$$t_{Fi}=(t_{Ai}-t_{Ri}-t_d)/2$
  
  $$$t_A=t_{R1}+t_{F1}$
  
  $$$t_R=t_A+t_d$
  
  $$$t_{Fi}=t_{Ai}-t_R$
  
  

Obviously, the reliability of such systems is theoretically worse than that of goniometric ones, especially in conditions of a complex sonar channel - such a system requires at least 3 successful signal reception to develop one solution.



Systems that determine the propagation time of a signal by method a) are least effective - each reference point should measure the distance to the desired object using the request-response method (or vice versa, the desired object alternately requests reference points).



The practical use of such systems is limited due to the large period of coordinate updating and low energy efficiency, but can be effectively applied in systems with a virtual long base . For example, in our demo project, where we determined the location of one of our micromodemsfloating on a bait boat with another such modem.

The first draft is described in one of our previous articles . There, the modem, GNSS module and radio module were combined using a board on the STM32.



In the new reincarnation of this project, the code was rewritten to Arduino UNO, and the navigation task is solved in an open source application .



Systems operating according to methods b) and c) are more efficient and have only drawbacks inherent in systems with pre-synchronization (b) - divergence of hours with time and with initiation by cable (c) - the need for electrical or optical communication (limitations associated with the availability of cable )



Systems with a distributed receiver operating according to method d) are most efficient from an energy point of view and have the greatest prospects.



Their work is as follows:

• at a given point in time, a leading reference point is selected, which requests the desired object at a time $$t R 1 , while the clocks of all reference points are synchronized (electrically or by radio signal, for example, GNSS);$t_{R1}$
• both the lead and slave reference points determine the times $$t R i arrival of the response signal of the positioned object;$t_{Ri}$
• distribution time $$t F 1 between the positioned object and the leading reference point is determined by the well-known formula, and the time is determined by the known propagation time$t_{F1}$$$t R of the radiation of the response signal, which then determines the times$t_R$$$t F i propagation of the response signal to the slave reference points.$t_{Fi}$

This scheme can be used to build positioning systems, and has the potential to build a system for a theoretically unlimited area (a real underwater GPS without any reservations!), By optimally choosing a leading reference point (for example, the closest to the previous calculated position of the positioned object).



In real rangefinding systems, the navigation task can be solved only by optimization methods. As a rule, the method of the poorest least squares ancestors in any variation is used.





The stability of the solution strongly depends on the initial approximation and, on the whole, is much more stable in type II systems, in view of the fact that, with the known vertical coordinate of the positioned object, the task translates into a flat one. In fact, today, systems built according to type I are not used in underwater navigation due to low reliability and accuracy.



At the moment, it is difficult to give an example of a purely rangefinder system; many contain a rangefinder method as one of the modes (for example, this one ). The production, installation and use of systems on the bottom base, as a rule, can be done only by large manufacturers, I will give as examples, along with the already mentioned, this , this , this , this and that one.

Due to the lack of information, it is difficult to unambiguously attribute any of the mentioned systems to one of the types, with a high probability they all work in the rangefinder mode of type IIa and, possibly, IId. In [1] and [2] it is reported that the systems of the manufacturer EvoLogics are of the IId type (with atomic clocks).



System Waterlinked GPS according to the manufacturer is a typical korotkobazisnuyu system, although, however, no precise data whether it works as a goniometer system with semi-acoustic measurement of the propagation time, or functions as a rangefinder, by type IIc.

Difference Range Finder Systems

From the point of view of the measured parameters, this type of system is similar to rangefinder systems, with the only difference being that instead of the signal propagation time $$t F uses signal arrival times$t_F$$$$t_A$ .



Adhering to the accepted scheme, we formalize the lists of measured parameters:

• Type I: $$$\{x_1..x_n\},\{y_1..y_n\},\{z_1..z_n\},\{t_{A1}..t_{An}\}$
• Type II: $$$\{x_1..x_n\},\{y_1..y_n\},\{z_1..z_n\},z_s,\{t_{A1}..t_{An}\}$

Where n is the number of control points, the minimum value for n = 3, $${ x 1 . . x n } , { y 1 . . y n } , { z 1 . . z n } - coordinates of reference points;$\{x_1..x_n\},\{y_1..y_n\},\{z_1..z_n\}$$${ t A 1 . . t A n } - times of arrival of a signal from either reference points to a positioned object (navigation systems), or times of arrival of a signal from a positioned object to reference points (positioning systems). For difference-rangefinder systems, unlike rangefinder systems, there is no such variety of subspecies due to different methods of measuring propagation time. Instead, there are two main ways to build a system cycle:$\{t_{A1}..t_{An}\}$

• a) synchronous, when the reference points have a synchronized clock;
• b) with an active base and a leading reference point. In this case, the leading reference point begins the cycle, and the followers in the chain emit a signal after receiving the signal from the previous one (for example, the hyperbolic radio navigation systems DECA, LORAN-C and Sovetskaya Chaika worked);

In systems operating on the difference-ranging principle, the so-called hyperbolic mode, i.e. the solution was defined as the intersection of hyperbolas (or hyperboloids), there are approximately a hundred hundred miles of work on this topic that the assiduous reader will find without problems on his own.



By analogy with the rangefinder method,





Today it is difficult to give an example of actually used systems operating according to type I, except for the already mentioned obsolete LORAN-C and Chaika (type Ib, which are not hydroacoustic, and global positioning systems - GPS, GLONASS, Galileo, Beidou (type Ia).



On the contrary, there are quite a lot of systems working on type IIa, for example, commercial, mass-produced by our RedWAVE , GIB SAR and EvoLogics , as well as earlier, purely research projects [48].



The most important advantage of difference-ranging systems is the ability to navigate an unlimited number of positioning objects in the case of an active base - according to the GNSS principle, which, for example, has been successfully implemented in our RedWAVE .



Another major advantage is the possibility of using only the receiving or only transmitting base, which, however, can be said about range-finding systems with preliminary synchronization.



Like rangefinder systems, differential rangefinder systems are even more sensitive to work outside the navigation base. The residual function outside the base is a gutter going to infinity, and finding a minimum there is not a problem at all - it can be found there at almost any point.



They say they don’t show themselves, but I'm not superstitious. Here is a track received by users of our RedWAVE differential rangefinding navigation system with not the most successful placement of buoys (base, reference points) and very inhospitable hydrology:







It is very clearly visible on the map that serious emissions occur exclusively outside the figure formed by reference points (buoys).

At the place of decision making

An important classification criterion is the location of the coordinates, which is often decisive in deciding whether to use a particular system. As a rule, navigation data - location data are primarily required where decisions are made on further actions.

Positioning systems. Tracking systems. Trekinig

This type of system allows tracking the underwater object. Such systems are most demanded when working with telecontrolled uninhabited underwater vehicles (TNPA), which are controlled by cable from operators from a surface post (shore, ship, etc.). Those. the place of decision-making is not at the positioned object.



Convenience here lies in the fact that, for example, a pinger or a responder beacon can be performed autonomously and does not require information and / or energy pairing with a carrier (TNLA), which undoubtedly simplifies integration.



In second place in the demand for tracking systems is the task of tracking divers, which occurs when it is necessary to control their movement, and if there is voice communication, and coordinate their actions.



In this regard, we are especially proud because our diving telephony combines voice communication and positioning - if we place small receiving buoys in the area of ​​diving operations, then after each release of the PTT (Push to talk) button, the diving device emits a navigation signal, which will determine its geographical location. By the way, this is a differential-ranging system of positioning, if we adhere to our classification.



The use of positioning systems is limited for autonomous uninhabited underwater vehicles, mainly due to the fact that AUVs usually contain decision logic and independently navigate if, however, a wireless telecontrol channel is not implemented. That is, navigation systems are generally more relevant for AUVs:

Navigation systems

In navigation systems, the position information of a positioned object is generated on the object itself. Basically, this is applicable for some diving tasks, undoubtedly applicable to a greater extent for AUVs and limitedly applicable to TNLA, when with sufficient direct hands of the robot manufacturer the degree of integration of the navigation system, it is possible to organize the transfer of navigation data via cable to the TNLA control point.



For example, the latter option is non-alternative if it is necessary to simultaneously operate several TNLA in one water area.



Examples of commercially available underwater sonar navigation systems include our RedWAVE and Vostok divers' drive systems, as well as the so-called silent LBL in the EvoLogics system.

Synthesis Methods

In some tasks, it is necessary to have location information at the same time both at the positioned object and at the control point. As an example, let us cite the management of an AUV flock, at least on the way to the place of basing, as well as some work that can be done with the help of divers.



The synthesis of navigation systems and positioning systems can occur according to two scenarios:



1) Actors carry out mutual positioning;



2) The solution obtained in one place is then transmitted to another place using electric, optical or sonar channels;



The second scenario is technically the easiest to implement and requires a generally simpler set of equipment. The only serious limitation is the need for temporary separation of the navigation transaction and the transmission of navigation data when using the sonar channel, and in the case of using another type of channel, there are restrictions associated with the presence of the cable.



When working in the first scenario, mutual positioning can be carried out, for example, using two probing antennas, when the distance is measured by one of the described methods - “request-response”, semi-acoustic or by preliminary synchronization ( UKB + UKB ).

Another way is to synthesize systems with different bases, for example UKB + KB, KB + DB, UKB + DB, KB + KB.



As a rule, when using DB systems with a bottom base, preliminary determination of the location of bottom stations is provided either using a surface direction-finding antenna (DB + UKB), using a KB system located on a ship (DB + KB), or using the virtual DB method (DB + VDB )



Another synthesis option is a system with a variable work pattern. An example is the task of driving and parking (including automatic) underwater vehicle. In drive mode, a distributed array of transceivers mounted on the bottom parking system can operate in a goniometric-rangefinder mode, as the so-called reverse ukb. In this case, the underwater vehicle receives signals from all elements of the measuring base and determines the angle of arrival of signals from the delays. When approaching a short distance, the system can already operate according to the rangefinder and / or difference-rangefinder scheme, while ensuring the maximum accuracy required in the parking mode inside the bottom parking system.



The prototype of such a system we just tested a couple of weeks ago in our pond, it was something like this:





Got a bunch of data that has yet to be processed qualitatively.

And our bonus!

As a presentation, I propose for deeply interested living code that can be used to implement navigation systems and positioning systems. The project is completely non-profit and started by us exclusively for educational purposes.



He lives at: https://github.com/ucnl/UCNLNav and recently, in a curious way, has almost become a meme hero:







In my defense, I want to say that it’s hard to compete with Okoloveb, mobile development and other fashionable things, so I so aggressively asked for asterisks. But, shrapnel - not shit, above your head, cornet! stars are not rubles, and more stars - more involved, more testing - more errors found, no palace - no palace .



Now there are:

- full implementation of conceived in C #

- implementation (constantly being added) of the main functionality in Rust





What the library can do:

• Convert from local coordinate system to geographical and vice versa;
• Solve direct and inverse geodesic problems on a sphere and an ellipsoid (Vincenty equation)

And the most useful:

• Solve TOA navigation problems (determining the position of the desired point by the known and distances to it) both in 2D (with a known Z coordinate) and in 3D.
• Solve TDOA navigation problems (determining the position of the desired point by distance differences.
• Solve a navigation problem using the VLBL method (Virtual Long Base).

PS

Traditionally, I want to remind you that it is very important to be sure that you are doing something useful, therefore, if readers are interested, I will write an article on the use of the library - let me know by voting.



I hope that Longrid came out not very difficult to read, well, or at least lifting.

PPS

I will be glad to listen to constructive criticism, wishes and suggestions.



Errors discovered, typos and inaccuracies in the articles ( not Human thanks to everyone who immediately reports on errors and typos found!).