 Dear reader!
Dear reader!
Today we are not meeting for the first time: tubs of
“We don’t know what you dream of becoming, our reader, - a pilot of a spaceship, or an explorer of the secrets of the atomic nucleus ...(c) Journal "Young Technician" No. 1 of 1956 (not)
... But one thing is firmly known: even if you dream of becoming an artist, writer, artist, then you still need to know the basics of machine learning ”
For the smallest:
Machine learning oil is data that, when “learning with a teacher”, should be structured into homogeneous “tables” (arrays) - input-output, or else, task-answer. This set is called Data Set. At universities, students are trained on ready-made date sets. These kits can be assembled independently. The program for collecting information is called the parser
For mothers:
Judging by the comments, most of the Khabrovites graduated from the Moscow Institute of Physics and Technology, and some more than once. This means that everyone already knows exactly who “survived on the Titanic” and how much “odnushka in America in 198x” cost. There is only one way out - to independently collect the date set. Otherwise, the post will stink with button accordions.
We decide on the task. In my example, we will try using a network to increase the resolution of the image. Accordingly, the set date will look like a set of “bad picture” - “good picture”.
Example
Task:

Answer:


Answer:

Image resolutions are different. Not all cars can pull heavy computing. So that performance and image sizes do not become a limitation, we define the sizes of our images. task 32x32 pixels, response 64x64.
A pixel (not always) is the sum of 3 numbers (see RGB), at the exit from the parser we should get 2 arrays with dimensions (N, 32, 32, 3) and (N, 64, 64, 3), where N is the number examples.
Next, I propose my simple program algorithms, and their not optimal, but workable solutions in Python:
Parser Algorithm:
It takes high-resolution images from the specified directory, divides them into small squares, while reducing the image resolution by half, saves both options to arrays.
1 - with reduced resolution, 2 - with full resolution.
Saves arrays to disk.
Input: photo folder
Output: 2 files containing date set x_train, y_train
1 - with reduced resolution, 2 - with full resolution.
Saves arrays to disk.
Input: photo folder
Output: 2 files containing date set x_train, y_train
Python code
import os import pickle import numpy as np from PIL import Image as PLi from tensorflow.keras.preprocessing import image as TFi path = './source/' temp_path = 'temp.bmp' l = 64 s = 32 x_train = [] y_train = [] def cut (image_path, coords): obj = PLi.open(image_path) cuted = obj.crop(coords) cuted.save(temp_path) large = TFi.load_img(temp_path, target_size=(l,l)) small = TFi.load_img(temp_path, target_size=(s,s)) y = TFi.img_to_array(large) x = TFi.img_to_array(small) y = y.reshape(l,l,3) x = x.reshape(s,s,3) y_train.append(y) x_train.append(x) filelist = sorted(os.listdir(path)) for name in filelist: try: target = PLi.open(path+name) width, height = target.size print(name+' '+str(width)+'x'+str(height)) h = height//l w = width//l for j in range(0, h+1): for i in range(0, w+1): crds = (l*i, l*j, l*(i+1), l*(j+1)) cut(path+name, crds) except BaseException: print ('Err '+name) x_train = np.array(x_train) y_train = np.array(y_train) x_train = x_train/255 y_train = y_train/255 print(x_train.shape) print(y_train.shape) with open('./x_train.pickle', 'wb') as f: pickle.dump(x_train, f) with open('./y_train.pickle', 'wb') as f: pickle.dump(y_train, f)
It should be noted that this algorithm "rapes" the hard drive, as it constantly overwrites. In my case, this is not important - there is a penny SSD, just for such cases. There is another caveat - you can’t just take and save a file of more than 4Gb in FAT32. There should not be too many source pictures.
The neural network training program algorithm:
Loads a set date from a specified directory
Creates a neural convolutional network
Using a date set, trains the network
Retains the best weights for the neural network
Input: 2 x_train, y_train files
Output: a file with weights of a trained neural network.
Creates a neural convolutional network
Using a date set, trains the network
Retains the best weights for the neural network
Input: 2 x_train, y_train files
Output: a file with weights of a trained neural network.
Python code
import pickle from tensorflow.keras.optimizers import Adam from tensorflow.python.keras.layers import Dense from tensorflow.python.keras.layers import Conv2D from tensorflow.python.keras.layers import UpSampling2D from tensorflow.python.keras.models import Sequential from tensorflow.keras.callbacks import ModelCheckpoint as ChPt with open('./x_train.pickle', 'rb') as f: x_train = pickle.load( f) with open('./y_train.pickle', 'rb') as f: y_train = pickle.load( f) model = Sequential([ Dense(3, input_shape=(32,32,3) ,activation='linear'), UpSampling2D(size=(2), data_format=None), Conv2D(3, (3, 3), activation='relu', padding='same'), ]) model.compile(loss='mse', optimizer=Adam(learning_rate=0.00002),metrics=['accuracy']) print(model.summary()) best_w=ChPt('./fcn_best.h5', monitor='val_accuracy', verbose=1, save_best_only=True, save_weights_only=True, mode='auto', save_freq='epoch') last_w=ChPt('./fcn_last.h5', monitor='val_accuracy', verbose=1, save_best_only=False, save_weights_only=True, mode='auto', save_freq='epoch') callbacks=[best_w, last_w] model.fit(x_train, y_train , steps_per_epoch=80, callbacks=callbacks, validation_split=0.25, batch_size=9, epochs=99, verbose=1, shuffle=True, use_multiprocessing=True )
The network architecture is elementary, but even it works, although the result has not gone far from interpolation.
Task:
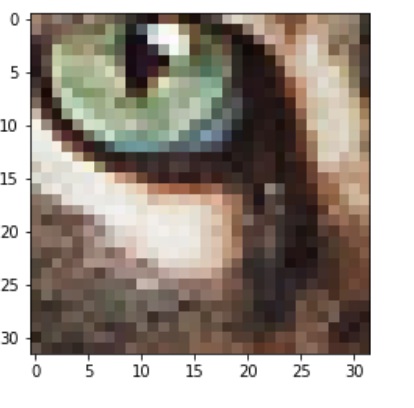
Correct answer:
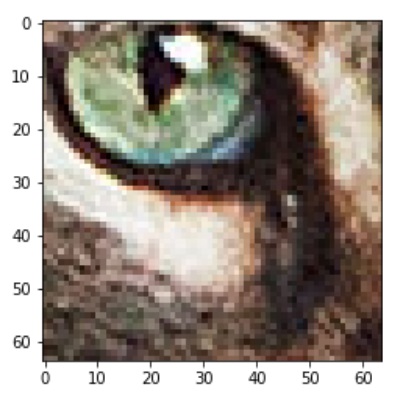
Neural Network Prediction:

In neural networks, the most interesting thing is to come up with an internal structure, which is what I propose the reader to do.
Then everything is simple - cut the picture, run the pieces through the grid with the loaded weights. In order for the result of the work of the neuron to be examined not one square, but the whole, the picture should be glued back.
The squares received in the answer are 64x64 points, the perimeter is 252 of 4096 - more than 6% of the points. This is an area with a low probability of prediction, as their neighbors are lost at the cutting stage. So, the resulting image will have stripes at the joints of the squares.

We will cover these places with predictions of the same picture, but cut with a shift by half a square.
Collector Algorithm:
Creates a neural network
From the indicated directories it loads the weights of the neural network and the target image, divides it into squares, uses these squares for prediction using the neural network. From the obtained squares it collects an improved image.
Saves the received image to disk.
Input: file with neural network weights, picture.
Exit: - picture with double resolution.
From the indicated directories it loads the weights of the neural network and the target image, divides it into squares, uses these squares for prediction using the neural network. From the obtained squares it collects an improved image.
Saves the received image to disk.
Input: file with neural network weights, picture.
Exit: - picture with double resolution.
Python code
import os import pickle import numpy as np from PIL import Image as PLi from tensorflow.keras.preprocessing import image as TFi from tensorflow.keras.optimizers import Adam from tensorflow.python.keras.layers import Dense from tensorflow.python.keras.layers import Conv2D from tensorflow.python.keras.layers import UpSampling2D from tensorflow.python.keras.models import Sequential from tensorflow.keras.callbacks import ModelCheckpoint as ChPt with open('./x_train.pickle', 'rb') as f: x_train = pickle.load( f) with open('./y_train.pickle', 'rb') as f: y_train = pickle.load( f) model = Sequential([ Dense(3, input_shape=(32,32,3) ,activation='linear'), UpSampling2D(size=(2), data_format=None), Conv2D(3, (3, 3), activation='relu', padding='same'), ]) model.compile(loss='mse', metrics=['accuracy']) model.load_weights('fcn_best.h5') path = './target/' temp_location = './target/temp/builded.bmp' out_location = "./target/temp/out.bmp" x0_build = [] x1_build = [] x2_build = [] x3_build = [] def build(image_path, coords, target): obj = PLi.open(image_path) builded = obj.crop(coords) builded.save(temp_location) img = TFi.load_img(temp_location, target_size=(32, 32)) x = np.array(TFi.img_to_array(img)) x = x.reshape(32,32,3) target.append(x) filelist = sorted(os.listdir(path)) for img in filelist: try: if img.endswith('.bmp') or img.endswith('.jpg'): image = PLi.open(path+img) width, height = image.size print(img + ' ' + str(width) + 'x' + str(height)) a = height//32 b = width//32 for j in range(1,a+2): for i in range(1,b+2): build(path+img, (32*(i-1),32*(j-1),32*i,32*j), x0_build) build(path+img, ((32*i-16),32*(j-1),(32*i+16),32*j), x1_build) build(path+img, (32*(i-1),32*j-16,32*i,32*j+16), x2_build) build(path+img, (32*i-16,32*j-16,32*i+16,32*j+16), x3_build) except BaseException: print ('Err ' + img) x0_build = np.array(x0_build) x0_build = x0_build.astype('float') x1_build = np.array(x1_build) x1_build = x1_build.astype('float') x2_build = np.array(x2_build) x2_build = x2_build.astype('float') x3_build = np.array(x3_build) x3_build = x3_build.astype('float') predictionsB = model.predict(x0_build) predictionsB1 = model.predict(x1_build) predictionsB2 = model.predict(x2_build) predictionsB3 = model.predict(x3_build) filelist = sorted(os.listdir(path)) n = 4 for img in filelist: try: if img.endswith('.bmp') or img.endswith('.jpg'): image = PLi.open(path+img) width, height = image.size out = PLi.new('RGB', (width*2, height*2)) a = height//32 b = width//32 k = 0 for i in range (0,a+1): for j in range (0,b+1): im = predictionsB[k] im = im.astype(np.uint8) _image = PLi.fromarray(im ,'RGB') _image_ = _image.crop((n,n,64-n,64-n)) im1 = predictionsB1[k] im1 = im1.astype(np.uint8) _image1 = PLi.fromarray(im1 ,'RGB') _image1_ = _image1.crop((n,n,64-n,64-n)) im2 = predictionsB2[k] im2 = im2.astype(np.uint8) _image2 = PLi.fromarray(im2 ,'RGB') _image2_ = _image2.crop((n,n,64-n,64-n)) im3 = predictionsB3[k] im3 = im3.astype(np.uint8) _image3 = PLi.fromarray(im3 ,'RGB') _image3_ = _image3.crop((n,n,64-n,64-n)) out.paste(_image_, (j*64+n,i*64+n)) out.paste(_image1_, ((j*64+32+n),(i*64+n))) out.paste(_image2_, ((j*64+n),(i*64+32+n))) out.paste(_image3_, ((j*64+32+n),(i*64+32+n))) k = k+1 out.save(out_location, quality=100) except BaseException: print ('Err ') print('Done')
The set of proposed programs is quite variable, with minimal interference in the code. For example, if you change the parser a little, it is easy to get a data set with noise, and then you can try to collect a “denoiser” or “noise”. I hope, dear reader, now you will have fun doing interesting experiments. And I can with impunity lay out my reasoning about the possible network architecture for the task stated above. But this is the next time.
7.3.