Two monumental works convinced many mathematicians to abandon the equal sign. Their goal is to reconstruct the foundations of discipline with the help of a weaker relationship - “equivalence”. And this process does not always go smoothly.
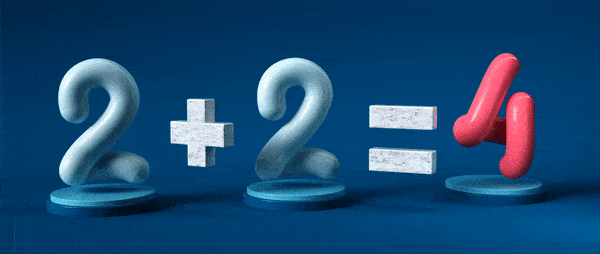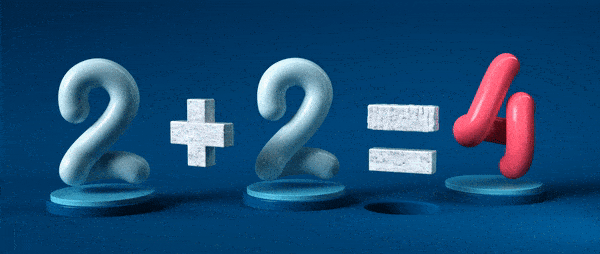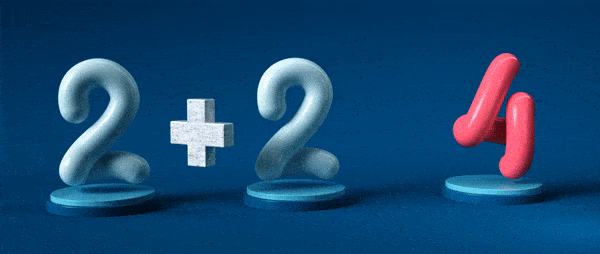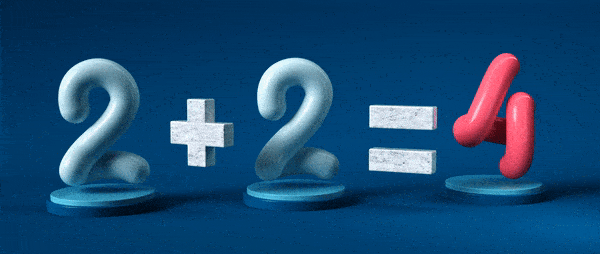
The equal sign is the cornerstone of mathematics. He seems to make a fundamental and consistent statement: these two entities are exactly the same.
However, the circle of mathematicians related to the equal sign, as to the initial error of mathematics, is expanding. They consider it to be an external gloss, hiding the important difficulties of the relationship of quantities - difficulties that can open up solutions to a huge number of problems. They want to reform math using a looser equivalence language.
“We spawned this idea of equality,” said Jonathan Campbell of Duke University. “And there should have been equivalence in its place.”
The most prominent figure in this community is Jacob Lurie . In July, 41-year-old Lurie resigned as a full-time employee at Harvard for a faculty position at the Princeton Institute for Advanced Studies, where some of the world's foremost mathematicians worked.
Ideas of such a scale as that of Lurie are rarely found in any field. In his books spanning thousands of pages full of technical details, he created a surprisingly different way from the usual way of understanding the most basic concepts of mathematics, going beyond the equal sign. “I think it seemed to him that this was the right way of thinking about mathematics,” said Michael Hopkins , a Harvard mathematician and postgraduate supervisor.
He published his first book, The Theory of Higher Topos , in 2009. A 944-page volume serves as an instruction for interpreting recognized areas of mathematics in the new language of "categories of infinity." In subsequent years, Lurie’s ideas penetrated a wide range of mathematical disciplines. Many mathematicians consider them indispensable for the future of this field. “No one will be the same after studying the categories of infinity,” said John Francis of Northwestern University,

Jacob Lurie
However, the spread of the categories of infinity revealed all the problems that a respected field of mathematics goes through, trying to absorb new bold ideas - especially an idea that challenges its most important concept. “There is a certain level of conservatism in the math community,” said Clark Barwick of the University of Edinburgh. “I don’t think that any group of mathematicians can be expected to quickly adopt any tool without convincing reasons.”
Although many mathematicians have accepted the categories of infinity, few have read the entire lengthy and extremely abstract texts of Lurie. As a result, part of the work based on his ideas turns out to be less rigorous than is accepted in mathematics.
“I heard people say: 'Lurie has it somewhere,'” said Inna Zakharevich , a mathematician at Cornell University. - And I say: 'Really? You refer to 8,000 pages of text. ' This is not a reference, this is an appeal to authority. ”
Mathematicians are still trying to realize both the breadth of Lurie’s ideas and the unique way of presenting them. They extract the essence of his presentation of the categories of infinity and present it in a new package so that more mathematicians can use it. In a sense, they carry out the necessary leadership, which is obliged to follow any revolution, translating the revolutionary text into the everyday code of laws. Thus, they create the future of mathematicians, based not on equality, but on equivalence.
Endless equivalence towers
Mathematical equality seems the least controversial of all ideas. Two beads plus one bead equals three beads. What else is there to talk about? However, the simplest ideas can be the most deceptive.
Since the end of the 19th century, the foundations of mathematics have been built on sets of objects called sets. Set theory sets the rules, or axiom, for the creation and handling of these sets. One of these axioms, for example, claims that you can add a set of one element to a set of two elements and get a new set of three elements: 2 + 1 = 3.
The formal way to demonstrate the equality of two quantities is to match pairs to each other. Match one bead to the right of the equal sign with one bead to the left. After all the comparisons, there will be no extra beads left.
Set theory recognizes that two sets of three objects each can be precisely matched to each other, but does not mean all the different possible ways of such a comparison. The first bead on the right can pick up a pair in the form of the first bead on the left, or match the first on the right with the second on the left, and so on (there can be six such pairs). To say that two plus one equals three, and end on this means not to see all the possible ways to equate them. “The problem is that there are many ways to pair up,” Campbell says. “And we forget them when we say equals.”
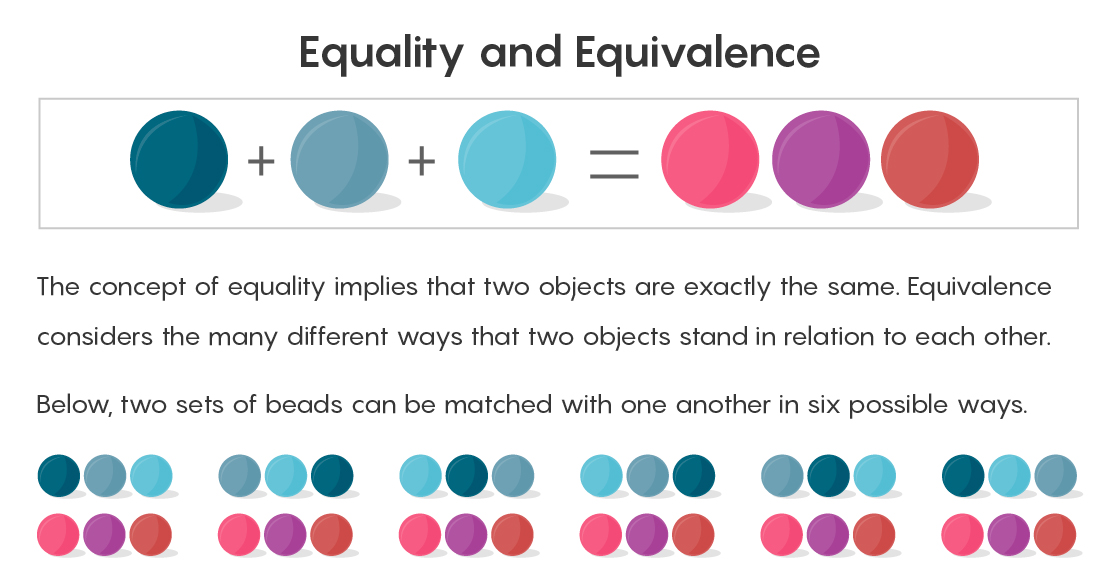
This is where equivalence comes into play. If equality is a clear relationship — two things are either equal or not — equivalence can be different.
When you precisely match each element of one set to each element of the other, you get strong equivalence. But, for example, in such a field of mathematics as homotopy , two forms (or geometric figures) are equivalent if one can be transformed into another by stretching or compression without breaks.
From the point of view of homotopy theory, a flat disk and a point in space are equivalent - the disk can be compressed to a point. However, you cannot match the points of a disc with the points of a point. After all, the disk of points has an infinite number, and a point is just one point.

Since the mid-20th century, mathematicians have been trying to develop an alternative to set theory in which mathematics would be easier to deal with in terms of equivalence. In 1945, mathematicians Samuel Eileberg and Saunders MacLane introduced a new fundamental object with built-in equivalence. They called it a category.
The category can be filled with anything. You can take the category of mammals, which will include all the hairy warm-blooded creatures that produce milk. Or you can create categories of mathematical objects: sets, geometric shapes, or numerical systems.
A category is a set with additional metadata: a description of all ways of matching one object to another, which includes a description of all the features by which two objects can be considered equivalent. Categories can also be imagined as geometric objects in which each category element is represented by a dot.
Imagine, for example, the surface of a ball. Each point on this surface can indicate its type of triangles. Paths between points express an equivalence relation between objects. From the point of view of category theory, we forget the specific way of describing an object and instead concentrate on what place the object occupies in relation to all other objects of this type.
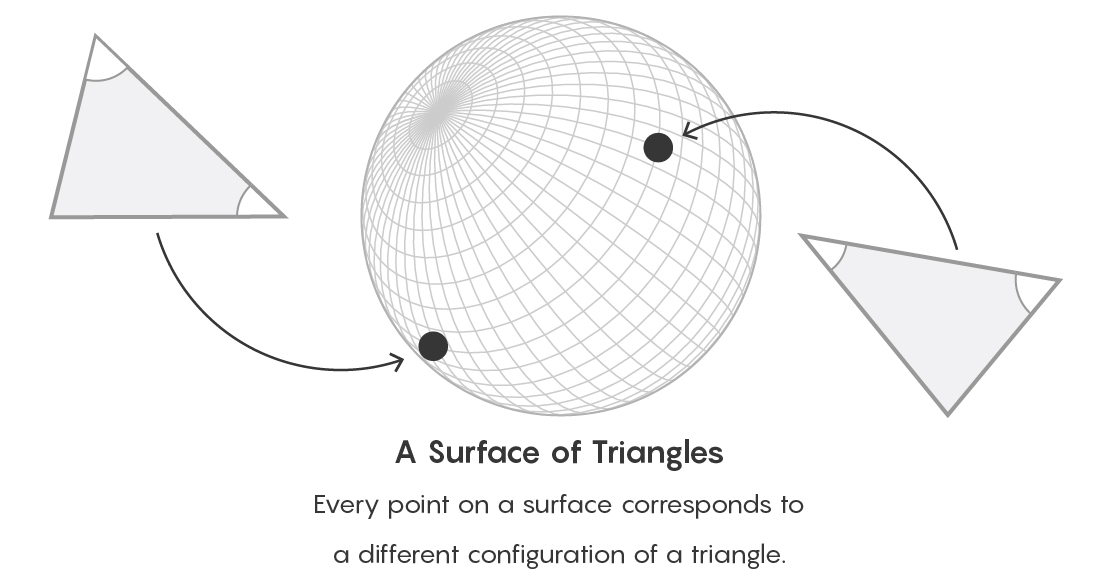
Each point on the surface corresponds to a particular type of triangles.
“We treat many things as things, although in reality they are a relationship between things,” Zakharevich said. - The phrase “my husband” means something that we consider an object, but you can think of it as a relationship. A certain part of it is determined by the relationship with me. "
The category version from Eilenberg and MacLane was well suited to working with strong equivalence options. But in the second half of the 20th century, mathematicians increasingly used weaker forms of equivalence, such as homotopy. “Mathematics is becoming more subtle, and inevitably we have a desire for more subtle ideas about ordinary things,” said Emily Riel, a mathematician at Johns Hopkins University. In these more subtle versions of equivalence, the amount of information about the relationship of two objects increases sharply. The rudimentary categories of Eilenberg and MacLane were not intended for this.
To see an increase in the amount of information, first remember our sphere, denoting different triangles. Two triangles are homotopically equivalent if one can be transformed into another by stretching or another deformation. Two points on a surface are homotopically equivalent if there is a path connecting them. By studying homotopic paths between points on a surface, you are actually studying the different ways that the triangles denoted by these points are connected to each other.
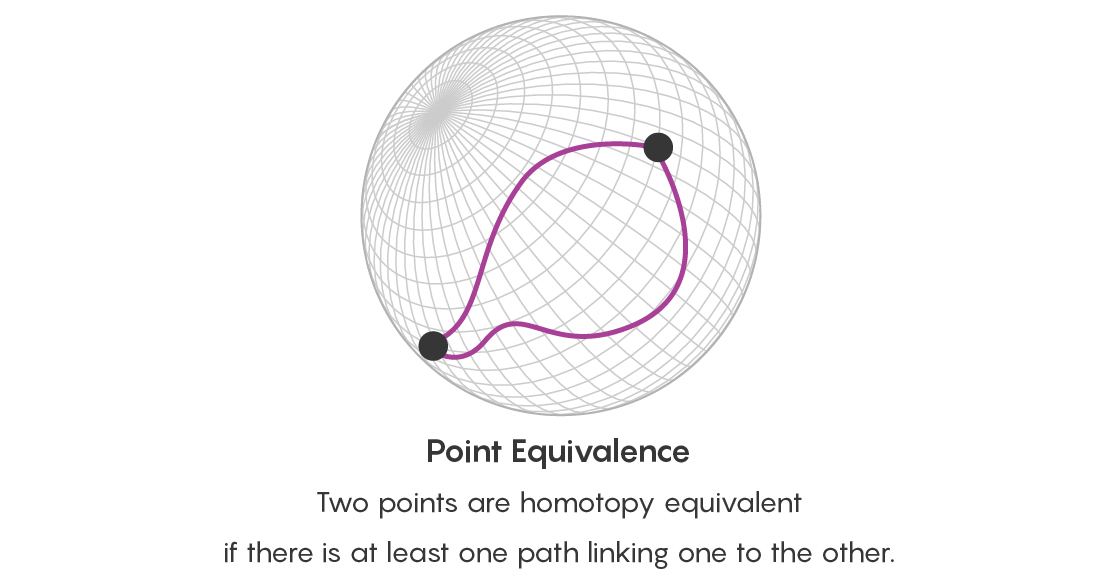
However, it is not enough to state that two points are connected in many equivalent ways. It is also necessary to think about the equivalence of all these paths. Therefore, in addition to the question of equivalence of points, you now ask the question of equivalence of two paths starting and ending at the same points - and is there a path connecting these paths. This path connecting the paths takes the form of a disk, the boundary of which are two of these paths.

You can develop this idea further. Two disks are equivalent if they are connected by a path - and this path will take the form of a three-dimensional object. Such three-dimensional objects can themselves be connected by four-dimensional paths (the path between two objects always has one dimension more than the objects themselves).
As a result, you build an endless tower of equivalence between equivalences. Arguing about the whole doctrine, you generate a general view of all the objects that you have marked with dots on the sphere.
“It's just a sphere, but it turns out that in order to understand the shape of a sphere, you need to go into infinity in some way,” said David Ben-Zvi of the University of Texas at Austin.
In the last decades of the 20th century, many mathematicians have worked on the theory of "categories of infinities" - on the fact that it is able to track the infinite tower of equivalences between equivalences. Some of them have achieved serious success. But only one reached the end.
Rewriting Math
The first work of Jacob Lurie in the categories of infinity was not very successful. On June 5, 2003, the 25-year-old scientist published a 60-page document entitled " On the Topos of Infinity " on the site of scientific preprints arxiv.org. There, he began to draft rough rules by which mathematicians could work with categories of infinity.
Not everyone accepted the first work the same way. Shortly after reading, Peter May , a mathematician at the University of Chicago, wrote to Lurie's supervisor, Michael Hopkins, that although Lurie's work contains interesting ideas, it looks unfinished and requires a more disciplined approach.
“I explained our comments to Mike, and he passed them on to Jacob,” May said.
It remains unknown whether Lurie took May's letter as a challenge, or if he had already planned his next step (Lurie rejected numerous requests for an interview). It is clear that after receiving critical comments, Lurie hit in a multi-year period of productivity, which later became legendary.
“I can’t get into Jacob’s brain, and so I don’t know exactly what he was thinking then,” May said. “But there is a huge difference between the draft that we reviewed and the final versions, which are already on a completely different mathematical level.”
In 2006, Lurie posted on arxiv.org a draft of “Theories of Higher Topos”. In this monumental work, he created the apparatus necessary to replace set theory with a new base for mathematics based on categories of infinity. “He created literally thousands of pages of this fundamental apparatus that we all use now,” said Charles Rezk, a mathematician at the University of Illinois at Urbana-Champaign, who did important work early on in developing infinity categories. “I can’t imagine how it’s possible to create a work like 'Theory of the Highest Topos' in a lifetime - and he created it in two or three years.”
Then in 2011, Lurie gave another, even longer work. In it, he reinvented algebra.
Algebra gives us a wonderful set of formal rules for manipulating equations. Mathematicians constantly use these rules to prove theorems. However, algebra does gymnastics on the fixed bars of the equal sign. Remove these bars, replacing them with a more ephemeral concept of equivalence, and some operations will become very complicated.
Take one of the first rules of algebra that children learn in school: associativity. The sum or product of three or more numbers does not depend on their grouping: 2 × (3 × 4) = (2 × 3) × 4.
It is easy to prove the associativity property for a list of three or more numbers if you are working with equality. This is difficult when you work even with the concept of strong equivalence. But when you move on to more subtle versions of equivalence, with their endless towers of paths connecting the paths, even a simple rule, similar to associativity, turns into a dark forest.
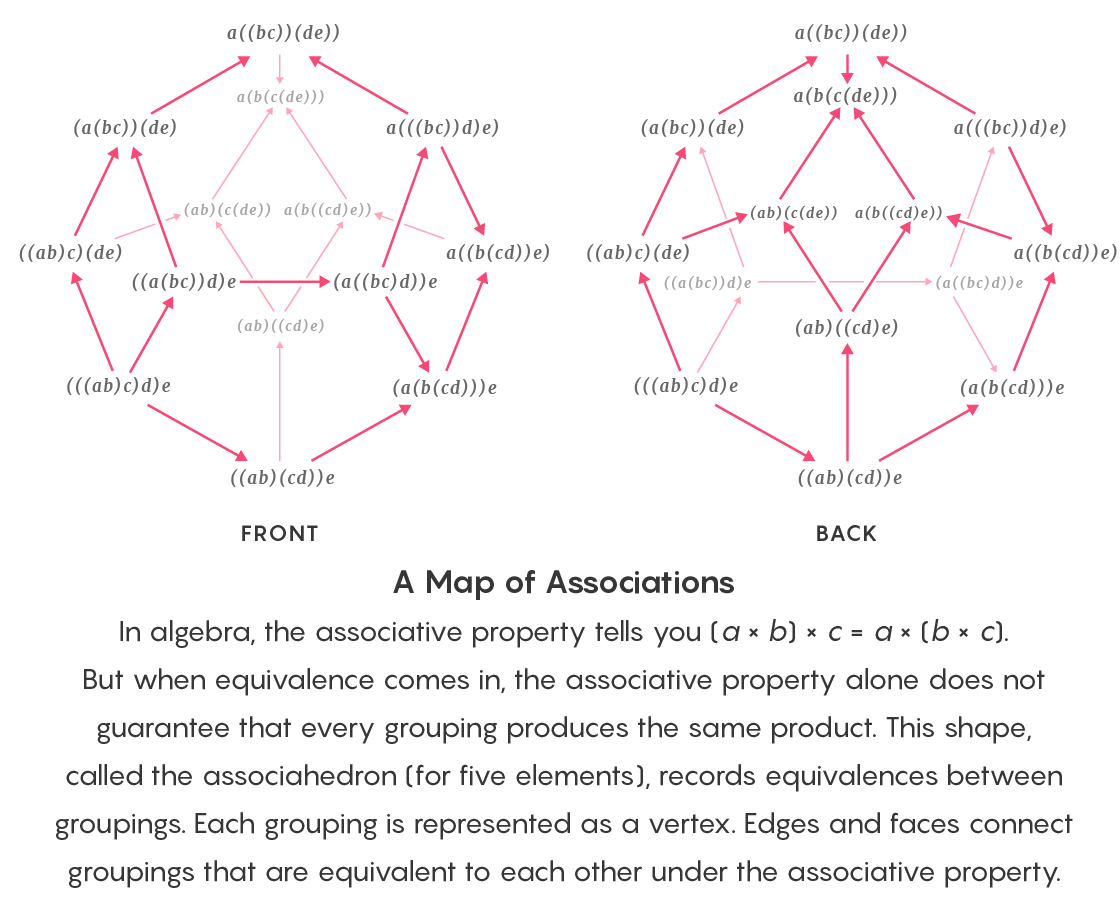
In algebra, associativity states that (a × b) × c = a × (b × c). But with the use of equivalence, associativity alone does not guarantee that any grouping of elements will yield the same multiplication result. This assocahedron contains group equivalence records. Each vertex corresponds to a grouping. Edges and faces combine groups associatively equivalent to each other.
“This makes the problem extremely complicated, which makes it impossible to work with this new version of mathematics,” said David Isla, a mathematician at the University of Montana.
In Higher Algebra, the latest version of which stretches over 1553 pages, Lurie developed an associativity option for infinity categories - as well as many other algebraic theorems that together form the basis of the mathematics of equivalences.
These two books produced the effect of an exploding bomb; such works give rise to a scientific revolution. “The scale was extraordinary,” Reel said. “It was the achievement of the Grothendieck level in algebraic geometry.”
However, revolution takes time, and, as mathematicians discovered after the publication of Lurie’s books, these years can be chaotic.
Digest a cow
Mathematicians are considered people with unambiguous thinking: the proof is either true or not; the idea either works or not. However, mathematicians are also ordinary people, and they react to new ideas in the same way as ordinary people: subjectively, emotionally, having personal motives.
“I think that many texts have been written about mathematicians in such a tone that they are looking for a sparkling crystal clear truth,” Campbell said. “But it doesn’t happen like that.” These are people with their own tastes, comfort zones, and they can deny things they don’t like for aesthetic or personal reasons. ”
In this regard, the work of Lurie has become a complex challenge to the community. In fact, it was provocative: here is a new and better way to do math. This message was addressed especially to mathematicians who spent their entire lives developing methods that Lurie excelled.
“People don’t always like to see the next generation rewrite their work, and this process is generating tension,” Francis said. “This is one of the features of the theory of categories of infinity - most of the previous works correspond.”
Lurie’s work was difficult to digest for other reasons. The volume of materials meant that mathematicians would have to spend years reading his books. It is almost impossible to demand from busy mathematicians who are in the middle of a career, and for graduate students who have only a few years to give a result that allows them to find a job, this is very risky.
Lurie's work was also very abstract, even compared to the extremely abstract nature of everything advanced mathematics studies. And not everyone liked it. “Many people thought Lurie’s work was abstract rubbish, and many simply fell in love with her,” said Campbell. “There were intermediate options, including those who didn't understand her at all.”

Emily reel
The scientific community is constantly accepting new ideas, but usually this happens slowly and with the feeling that everyone is moving at the same time. The emergence of new ideas creates difficulties for the intellectual apparatus of the community. “A lot of new things come up right away - it's like a boa trying to digest a cow,” Campbell said. “A huge mass passes through the community.”
If you are a mathematician who believes that Lurie’s approach is the best way to do mathematics, then your path forward will be lonely. Few people read Lurie’s work, there were no textbooks to recount them briefly, and no seminars to help you get your bearings. “There was only one way to study all this in great detail - to sit down and do everything yourself,” said Peter Heine, a graduate student at MIT who spent a year reading Lurie’s work. - I think this is the most difficult. "It’s not easy to sit down, and to figure it out yourself yourself - namely, to sit down and read 800 pages of Theory of the Topos Theory yourself.
Like many new inventions, the theory of higher topos requires mathematicians to actively interact with the apparatus, which allows it to work. This is how to make every 16-year-old boy dreaming of a driver’s license first learn how to sort out the engine. “If there was a friendlier version of all this, then the theory would immediately become more accessible to wider mathematical circles,” said Dennis Gatesgory, a Harvard mathematician who worked with Lurie.
When people began to read Lurie’s work and use the categories of infinity in their studies, other problems appeared. Mathematicians built their work on the basis of the categories of infinity. Magazine reviewers received these papers and asked: what is it?
“There was a situation in which the work either returned from the magazines with absurd reviews, from which a complete lack of understanding was visible, or it took several years to publish them,” said Barvik. “It can be a lot of inconvenience, because the unpublished work that has been on your site for years looks more and more ridiculous.”
However, the biggest problem was not unpublished works, but works using the categories of infinity, and published - but containing errors.
The books of Lurie are the only authoritative source of information on the categories of infinity. They are strict, but it is difficult to fully understand them. And they are especially poorly suited to the role of instructions that could be referenced - it is difficult to search for certain theorems, or to verify that a certain application of the categories of infinity encountered in someone's work really works.
“Most mathematicians working in this area have not read Lurie systematically,” said Andre Joyal , a mathematician at the University of Quebec in Montreal, whose early work was a key ingredient in Lurie's books. “It takes a lot of time and energy, so we just assume that everything that is written in his books is true - because almost every time we check something, it turns out to be true. In fact, every time. "
The inaccessibility of Lurie's books led to inaccuracies in some of the studies that followed. Lurie’s books are hard to read, hard to quote, and hard to use to test other people's work.
“The general literature on the topic of categories of infinity seems messy,” Zakharevich said.
Despite all its formalism, mathematics should not be a sacred text that only priests can read. In this area not only thick volumes are required, but also booklets, not only the initial revelations, but also the interpretations of their descriptions. In the meantime, the theory of infinity categories exists, for the most part, in the form of several large books on a shelf.
“You can take the approach. 'Jacob will tell you what to do, and everything is in order,' said Rezk. “Or you can decide that 'We don’t know how to present our topic well enough so that people can use it.”
However, few mathematicians were able to accept the challenge and make the category of infinity a technology that more people from their field of study could use.
User Friendly Theory
In order to translate the categories of infinities into an object capable of real mathematical work, Lurie had to prove the theorems associated with them. And for this, he had to choose a landscape on which to create this evidence - just like a person who is engaged in geometry, it is necessary to choose a coordinate system for work. Mathematicians call this model selection.
Lurie developed the categories of infinities on the model of quasicategories.Other mathematicians before him developed the categories of infinities on other models. And although their work was not as comprehensive as that of Lurie, in some situations it is easier to deal with them. “Jacob chose a model and checked that everything works in it, but often it is not the easiest,” said Zakharevich.
In geometry, mathematicians clearly understand how to move between different coordinate systems. They also proved that theorems proved in some conditions work in others.
For infinity categories, such guarantees do not exist. However, when mathematicians write works using the categories of infinities, they often easily switch between models, assuming (but not proving) the portability of the results. “People don’t specify what they’re doing, they switch between all these different models, and they say: Ah, it’s the same thing,” Heine said. “But that is not proof.”
Over the past six years, a couple of mathematicians have tried to obtain these guarantees. Ryl and Dominic Verityfrom McUyra University in Australia, developed a way to describe the categories of infinities, overcoming the difficulties that appeared in previous platforms using certain models. Their work, based on the previous works of Barvik and others, proved that many of the theorems of “Theories of Higher Topos” remain true regardless of the model used. And they prove this compatibility in an appropriate way: “We study the categories of infinity, the objects of which are themselves the categories of infinity,” said Ril. “Category theory bites its tail.”
Riel and Verity hope to develop the theory of the categories of infinities in yet another way. They choose aspects of the theory that work regardless of model. Such a presentation, which is independent of the model, has a convenient quality of instant applicability, which, they hope, will attract mathematicians to this area of research who stayed away from it when the only input was The Higher Topos Theory.
“To get into this world, you need to overcome the moat,” said Hopkins. “And they do that lower the bridge.”
Ryl and Verity plan to finish work next year. Meanwhile, Lurie recently began work on the Kerodon project ., which he planned to turn into a kind of reference book on the theory of the highest category, similar to Wikipedia. Thirteen years after the Higher Topos Theory formalized the mathematics of equivalence, these initiatives are trying to refine and disseminate these ideas - to make the mathematics of equivalence more accessible.
“Genius has an important role in the development of mathematics, but knowledge itself is the result of the work of the entire community,” said Zhoyal. “The real goal of knowledge is to become knowledge of the whole community, and not to belong to one or two people.”