Oh this Newton's method
A lot has been written about numerical optimization methods. This is understandable, especially against the background of the successes recently demonstrated by deep neural networks. And it is very gratifying that at least some enthusiasts are interested not only in how to bomb their neural network on the frameworks that have gained popularity in these Internet, but also how and why it all works. However, I recently had to note that in posing issues related to the training of neural networks (and not only with training, and not only networks), including on Habré, more and more often a number of “well-known” statements are used for forwarding, the validity of which to put it mildly, doubtful. Among such dubious statements:
etc. Than to continue this list, it’s better to get down to business. In this post we will consider the second statement, since I only met him at least twice in Habré. The first question I will touch upon only in that part as regards the Newton method, since it is much more extensive. The third and the rest will be left until better times.
The focus of our attention will be the task of unconditional optimization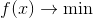
where 
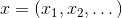- a point of vector space, or simply - a vector. Naturally, this task is easier to solve, the more we know about 
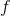. It is usually assumed to be differentiable with respect to each argument 
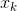, and as many times as needed for our dirty deeds. It is well known that a necessary condition for that at a point 
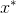minimum is reached, is the equality of the gradient of the function 
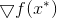at this point zero. From here we instantly get the following minimization method:
Solve the equation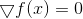
.
The task, to put it mildly, is not an easy one. Definitely not easier than the original. However, at this point, one can immediately note the connection between the minimization problem and the problem of solving a system of nonlinear equations. This connection will come back to us when considering the Levenberg-Marquardt method (when we get to it). In the meantime, remember (or find out) that one of the most commonly used methods for solving systems of nonlinear equations is Newton's method. It consists in the fact that to solve the equation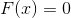
we starting from some initial approximation 
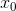build a sequence
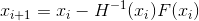- Newton's explicit method
or
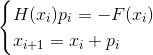- Newton's implicit method
Where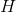
- matrix made up of partial derivatives of a function 
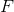. Naturally, in the general case, when the system of nonlinear equations is simply given to us in sensations, require something from the matrix 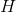we are not entitled. In the case when the equation is a minimum condition for some function, then we can state that the matrix 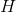symmetrical. But not more.
Newton's method for solving systems of nonlinear equations has been studied quite well. And here's the thing - for its convergence the positive definiteness of the matrix is not required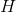 . Yes, and can not be required - otherwise he would have been worthless. Instead, there are other conditions that ensure local convergence of this method and which we will not consider here, sending interested people to specialized literature (or in a commentary). We get that statement 2 is false.
So?
Yes and no. The ambush here in the word is local convergence before the word. It means that the initial approximation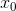 must be “close enough” to the solution, otherwise at each step we will be further and further removed from it. What to do? I will not go into details of how this problem is solved for systems of non-linear equations of a general form. Instead, back to our optimization task. The first mistake of statement 2 is actually that, usually speaking about the Newton method in optimization problems, it means its modification - the damped Newton method, in which the sequence of approximations is constructed according to the rule
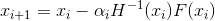- Newton's explicit damped method
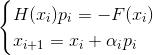- Newton's implicit damped method
Here is the sequence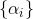
is a parameter of the method and its construction is a separate task. In minimization problems, natural when choosing 
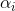there will be a requirement that at each iteration the value of the function f decreases, i.e. 
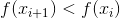. A logical question arises: is there such a (positive) 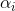? And if the answer to this question is positive, then 
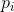called the direction of descent. Then the question can be posed in this way:
when is the direction generated by Newton's method the direction of descent?
And to answer it you will have to look at the minimization problem from another side.
For the minimization problem, this approach seems quite natural: starting from some arbitrary point, we choose the direction p in some way and take a step in this direction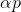
. If 
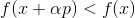then take 
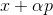as a new starting point and repeat the procedure. If the direction is chosen arbitrarily, then such a method is sometimes called the random walk method. It is possible to take unit basis vectors as a direction — that is, to take a step in only one coordinate, this method is called the coordinate descent method. Needless to say, they are ineffective? In order for this approach to work well, we need some additional guarantees. To do this, we introduce an auxiliary function 
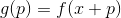. I think it’s quite obvious that minimization 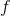completely equivalent to minimizing 
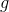. If 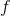differentiable then 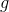can be represented as
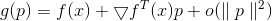
and if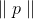
small enough then 
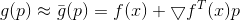. We can now try to replace the minimization problem 
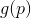the task of minimizing its approximation (or model ) 
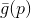. By the way, all methods based on the use of the model 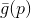called gradient. But the trouble is, 
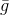Is a linear function and, therefore, it has no minimum. To solve this problem, we add a restriction on the length of the step that we want to take. In this case, this is a completely natural requirement - after all, our model more or less correctly describes the objective function only in a sufficiently small neighborhood. As a result, we obtain an additional problem of conditional optimization:
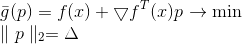
This task has an obvious solution: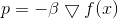
where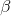 
- factor guaranteeing the fulfillment of the constraint. Then iterations of the descent method take the form
,
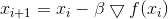in which we learn the well-known gradient descent method . Parameter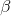 , which is usually called the descent speed, has now acquired a completely understandable meaning, and its value is determined from the condition that the new point lies on a sphere of a given radius, circumscribed around the old point.
Based on the properties of the constructed model of the objective function, we can argue that there is such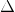
, even if very small, what if 
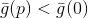then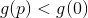 
. It is noteworthy that in this case the direction in which we will move does not depend on the size of the radius of this sphere. Then we can choose one of the following ways:
The first approach is typical for the methods of the trust region , the second leads to the formulation of the auxiliary problem of the so-called linear search (LineSearch) . In this particular case, the differences between these approaches are small and we will not consider them. Instead, pay attention to the following:
why, in fact, are we looking for an offset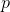
lying exactly on the sphere?
In fact, we could well replace this restriction with the requirement, for example, that p belong to the surface of the cube, i.e.,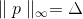
(in this case, this is not too reasonable, but why not), or some elliptical surface? This already seems quite logical if we recall the problems that arise when minimizing gully functions. The essence of the problem is that along some coordinate lines the function changes much faster than along others. Because of this, we get that if the increment should belong to the sphere, then the quantity 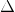at which the “descent” is provided must be very small. And this leads to the fact that achieving a minimum will require a very large number of steps. But if instead we take a suitable ellipse as a neighborhood, then this problem will magically come to naught.
By the condition that the points of the elliptic surface belong, can be written as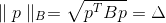
where 
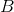Is some positive definite matrix, also called a metric. Norm 
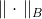called the elliptic norm induced by the matrix 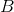. What kind of matrix is it and where to get it from - we will consider later, and now we come to a new task.
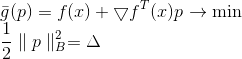
The square of the norm and the 1/2 factor are here solely for convenience, so as not to mess with the roots. Applying the Lagrange multiplier method, we obtain the bound problem of unconditional optimization
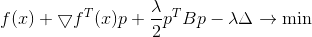
A necessary condition for a minimum for it is
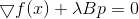, or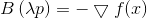 
from where
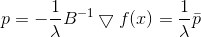
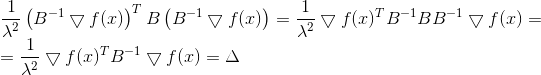
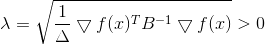
Again we see that the direction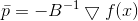
, in which we will move, does not depend on the value 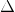- only from the matrix 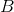. And again, we can either pick up 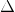that is fraught with the need to calculate 
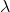and explicit matrix inversion 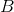, or solve the auxiliary problem of finding a suitable bias 
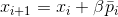. Insofar as 
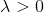, the solution to this auxiliary problem is guaranteed to exist.
So what should it be for matrix B? We restrict ourselves to speculative ideas. If the objective function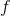 - quadratic, that is, it has the form 
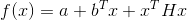where 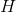positive definite, then it is obvious that the best candidate for the role of the matrix 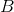is hessian 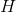, since in this case one iteration of the descent method we have constructed is required. If H is not positive definite, then it cannot be a metric, and the iterations constructed with it are iterations of the damped Newton method, but they are not iterations of the descent method. Finally, we can give a rigorous answer to
Question: Does the Hessian matrix in the Newton method have to be positive definite?
Answer: no, it is not required in either the standard or the damped Newton method. But if this condition is satisfied, then the damped Newton method is a descent method and has the property of global , and not just local convergence.
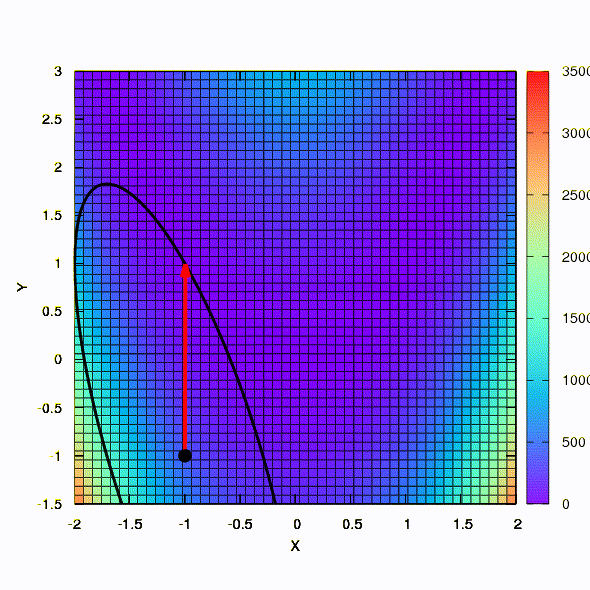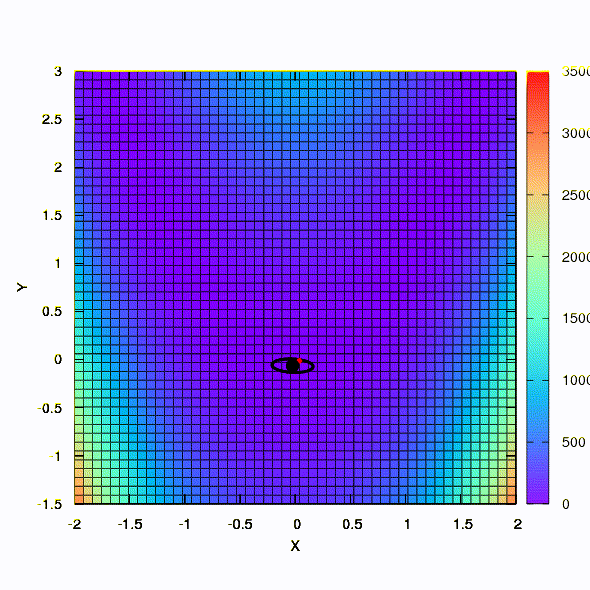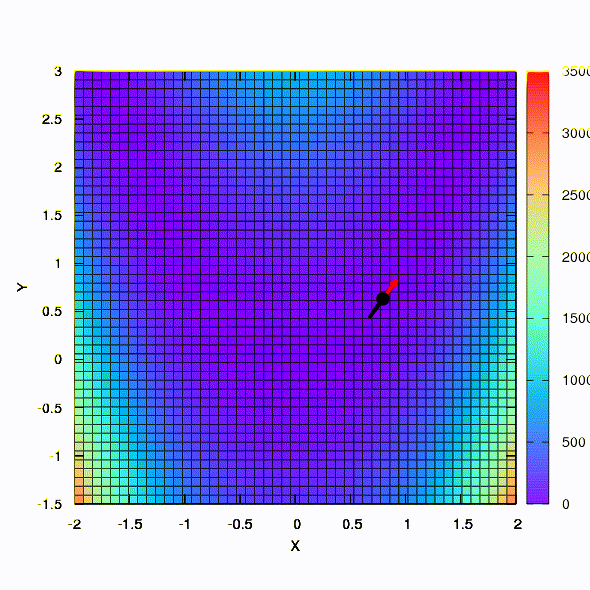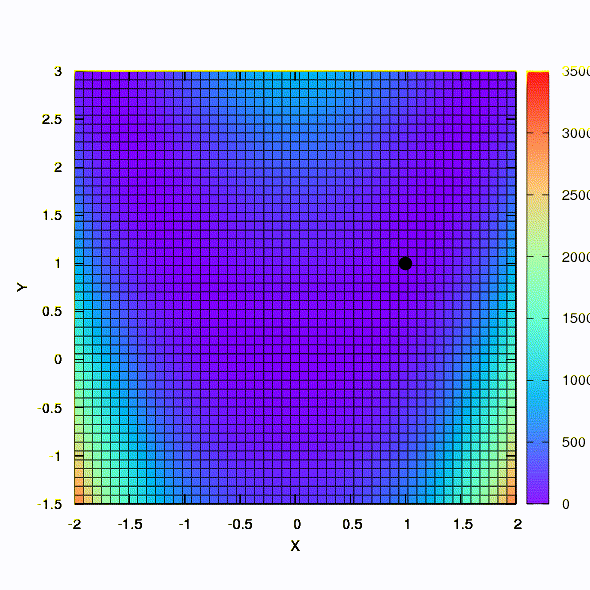
As an illustration, let’s see what confidence regions look like if the well-known Rosenbrock function is minimized by gradient descent and Newton’s methods, and how the shape of the regions affects the convergence of the process.
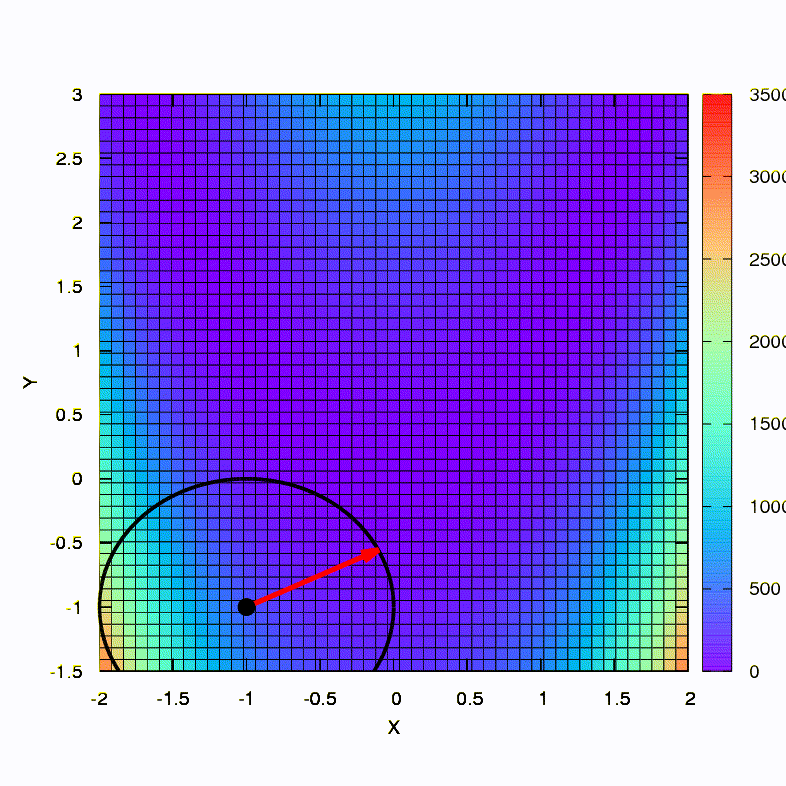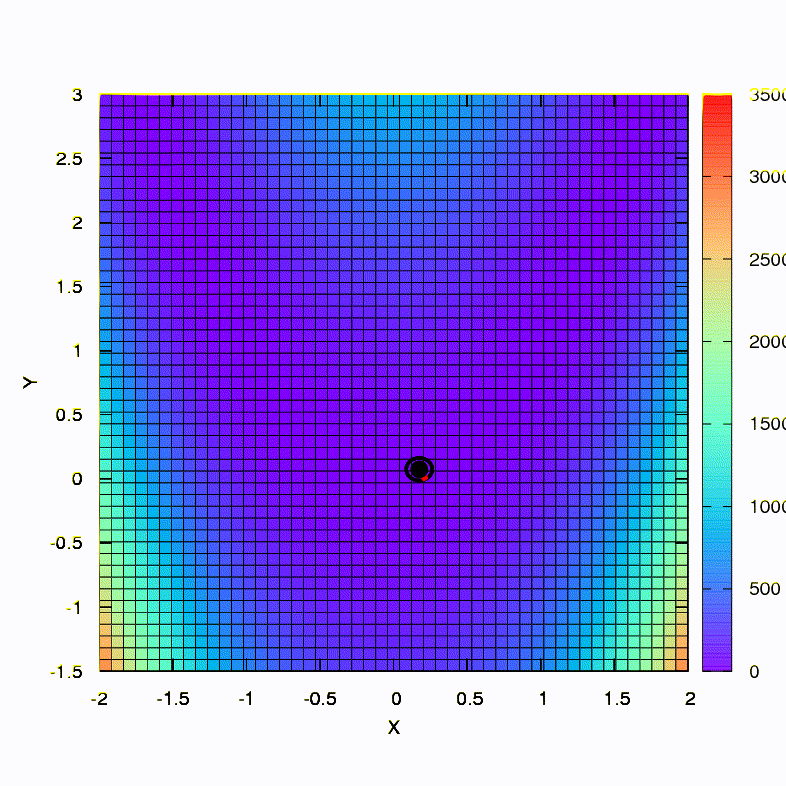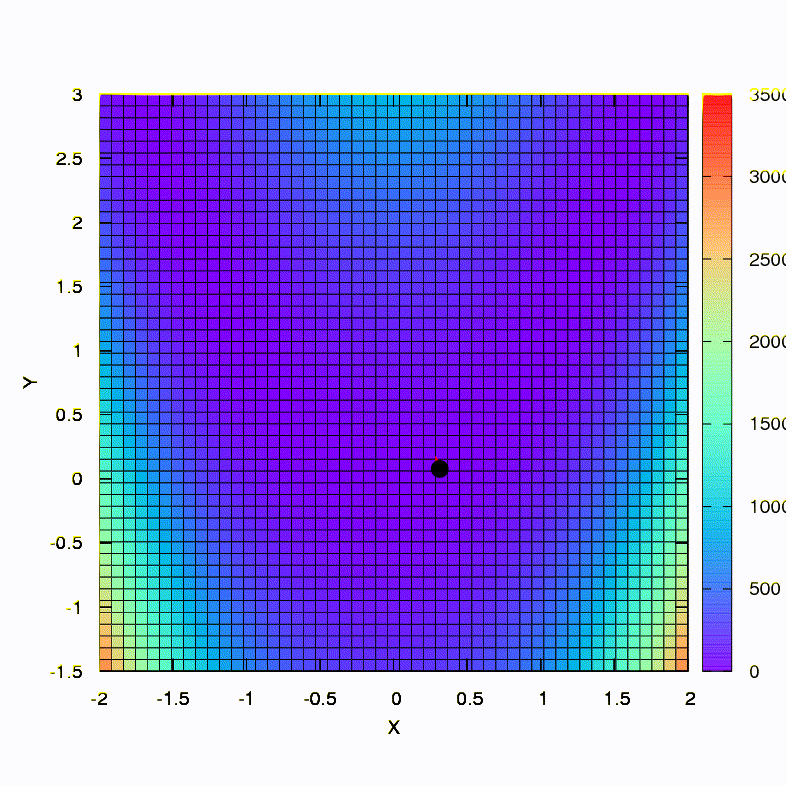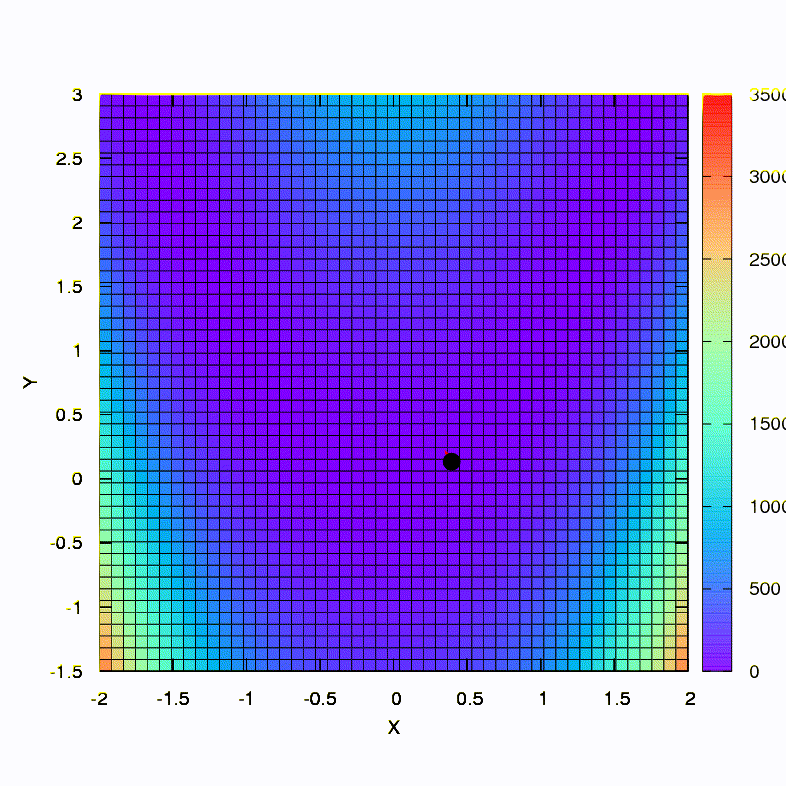
This is how the descent method behaves with a spherical confidence region, it is also a gradient descent. Everything is like a textbook - we are stuck in a canyon.
And this we get if the confidence region has the shape of an ellipse defined by the Hessian matrix. This is nothing more than an iteration of the damped Newton method.
The only unresolved question is what to do if the Hessian matrix is not positive definite. There are many options. The first is to score. Maybe you're lucky and Newton's iterations will converge without this property. This is quite real, especially at the final stages of the minimization process, when you are already close enough to a solution. In this case, iterations of the standard Newton method can be used without bothering with the search for a neighborhood admissible for descent. Or use iterations of the damped Newton method in the case of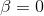
, that is, in the case when the obtained direction is not the descent direction, change it, say, to an anti-gradient. Just do not have to explicitly check whether the Hessian is positive definite according to the Sylvester criterion , as was done here !!! . It is wasteful and pointless.
More subtle methods involve constructing a matrix, in a sense close to the Hessian matrix, but possessing the property of positive definiteness, in particular, by correcting eigenvalues. A separate topic is the quasi-Newtonian methods, or variable metric methods, which guarantee the positive definiteness of the matrix B and do not require the calculation of the second derivatives. In general, a detailed discussion of these issues goes well beyond the scope of this article.
Yes, and by the way, it follows from what has been said that the damped Newton method with positive definiteness of the Hessian is a gradient method . Like quasi-Newtonian methods. And many others, based on a separate choice of direction and step size. So contrasting the Newton method with gradient terminology is incorrect.
The Newton method, which is often remembered when discussing minimization methods, is usually not the Newton method in its classical sense, but the descent method with the metric specified by the Hessian of the objective function. And yes, it converges globally if the Hessian is everywhere positive definite. This is possible only for convex functions, which are much less common in practice than we would like, so in the general case, without the appropriate modifications, the application of the Newton method (we will not break away from the collective and continue to call it that) does not guarantee the correct result. Training neural networks, even shallow ones, usually leads to non-convex optimization problems with many local minima. And here is a new ambush. Newton's method usually converges (if converges) quickly. I mean very fast. And this, oddly enough, is bad, because we come to a local minimum in several iterations. And it for functions with complex terrain can be much worse than the global one. Gradient descent with linear search converges much more slowly, but is more likely to “skip” the ridges of the target function, which is very important in the early stages of minimization. If you have already well reduced the value of the objective function, and the convergence of the gradient descent has slowed significantly, then here the change in the metric may well accelerate the process, but this is for the final stages.
Of course, this argument is not universal, not indisputable, and in some cases even incorrect. As well as the statement that gradient methods work best in learning problems.
- Methods of the second and more orders do not work well in the tasks of training neural networks. Because.
- The Newton method requires positive definiteness of the Hessian matrix (second derivatives) and therefore does not work well.
- The Levenberg-Marquardt method is a compromise between gradient descent and the Newton method and is generally heuristic.
etc. Than to continue this list, it’s better to get down to business. In this post we will consider the second statement, since I only met him at least twice in Habré. The first question I will touch upon only in that part as regards the Newton method, since it is much more extensive. The third and the rest will be left until better times.
The focus of our attention will be the task of unconditional optimization
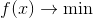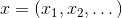where - a point of vector space, or simply - a vector. Naturally, this task is easier to solve, the more we know about 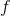. It is usually assumed to be differentiable with respect to each argument 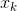, and as many times as needed for our dirty deeds. It is well known that a necessary condition for that at a point 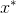minimum is reached, is the equality of the gradient of the function 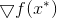at this point zero. From here we instantly get the following minimization method:
Solve the equation
.
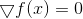The task, to put it mildly, is not an easy one. Definitely not easier than the original. However, at this point, one can immediately note the connection between the minimization problem and the problem of solving a system of nonlinear equations. This connection will come back to us when considering the Levenberg-Marquardt method (when we get to it). In the meantime, remember (or find out) that one of the most commonly used methods for solving systems of nonlinear equations is Newton's method. It consists in the fact that to solve the equation
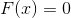we starting from some initial approximation 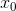build a sequence
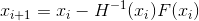- Newton's explicit method
or
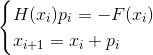- Newton's implicit method
Where
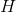- matrix made up of partial derivatives of a function 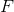. Naturally, in the general case, when the system of nonlinear equations is simply given to us in sensations, require something from the matrix 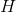we are not entitled. In the case when the equation is a minimum condition for some function, then we can state that the matrix 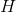symmetrical. But not more.
Newton's method for solving systems of nonlinear equations has been studied quite well. And here's the thing - for its convergence the positive definiteness of the matrix is not required
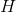. Yes, and can not be required - otherwise he would have been worthless. Instead, there are other conditions that ensure local convergence of this method and which we will not consider here, sending interested people to specialized literature (or in a commentary). We get that statement 2 is false.
So?
Yes and no. The ambush here in the word is local convergence before the word. It means that the initial approximation
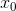must be “close enough” to the solution, otherwise at each step we will be further and further removed from it. What to do? I will not go into details of how this problem is solved for systems of non-linear equations of a general form. Instead, back to our optimization task. The first mistake of statement 2 is actually that, usually speaking about the Newton method in optimization problems, it means its modification - the damped Newton method, in which the sequence of approximations is constructed according to the rule
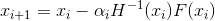- Newton's explicit damped method
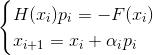- Newton's implicit damped method
Here is the sequence
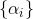is a parameter of the method and its construction is a separate task. In minimization problems, natural when choosing 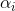there will be a requirement that at each iteration the value of the function f decreases, i.e. 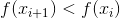. A logical question arises: is there such a (positive) 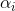? And if the answer to this question is positive, then 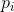called the direction of descent. Then the question can be posed in this way:
when is the direction generated by Newton's method the direction of descent?
And to answer it you will have to look at the minimization problem from another side.
Descent methods
For the minimization problem, this approach seems quite natural: starting from some arbitrary point, we choose the direction p in some way and take a step in this direction
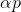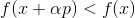. If then take 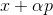as a new starting point and repeat the procedure. If the direction is chosen arbitrarily, then such a method is sometimes called the random walk method. It is possible to take unit basis vectors as a direction — that is, to take a step in only one coordinate, this method is called the coordinate descent method. Needless to say, they are ineffective? In order for this approach to work well, we need some additional guarantees. To do this, we introduce an auxiliary function 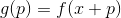. I think it’s quite obvious that minimization 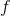completely equivalent to minimizing 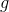. If 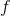differentiable then 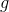can be represented as
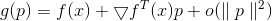
and if
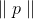small enough then 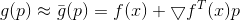. We can now try to replace the minimization problem 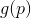the task of minimizing its approximation (or model ) 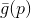. By the way, all methods based on the use of the model 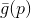called gradient. But the trouble is, 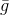Is a linear function and, therefore, it has no minimum. To solve this problem, we add a restriction on the length of the step that we want to take. In this case, this is a completely natural requirement - after all, our model more or less correctly describes the objective function only in a sufficiently small neighborhood. As a result, we obtain an additional problem of conditional optimization:
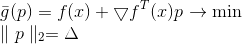
This task has an obvious solution:
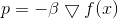where 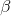- factor guaranteeing the fulfillment of the constraint. Then iterations of the descent method take the form
,
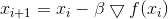in which we learn the well-known gradient descent method . Parameter
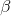, which is usually called the descent speed, has now acquired a completely understandable meaning, and its value is determined from the condition that the new point lies on a sphere of a given radius, circumscribed around the old point.
Based on the properties of the constructed model of the objective function, we can argue that there is such
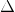, even if very small, what if 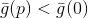then 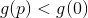. It is noteworthy that in this case the direction in which we will move does not depend on the size of the radius of this sphere. Then we can choose one of the following ways:
- Select according to some method the value .
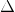- Set the task of choosing the appropriate value 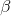, providing a decrease in the value of the objective function.
The first approach is typical for the methods of the trust region , the second leads to the formulation of the auxiliary problem of the so-called linear search (LineSearch) . In this particular case, the differences between these approaches are small and we will not consider them. Instead, pay attention to the following:
why, in fact, are we looking for an offset
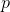lying exactly on the sphere?
In fact, we could well replace this restriction with the requirement, for example, that p belong to the surface of the cube, i.e.,
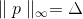(in this case, this is not too reasonable, but why not), or some elliptical surface? This already seems quite logical if we recall the problems that arise when minimizing gully functions. The essence of the problem is that along some coordinate lines the function changes much faster than along others. Because of this, we get that if the increment should belong to the sphere, then the quantity 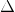at which the “descent” is provided must be very small. And this leads to the fact that achieving a minimum will require a very large number of steps. But if instead we take a suitable ellipse as a neighborhood, then this problem will magically come to naught.
By the condition that the points of the elliptic surface belong, can be written as
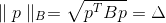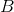where Is some positive definite matrix, also called a metric. Norm 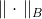called the elliptic norm induced by the matrix 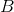. What kind of matrix is it and where to get it from - we will consider later, and now we come to a new task.
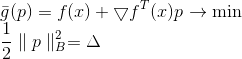
The square of the norm and the 1/2 factor are here solely for convenience, so as not to mess with the roots. Applying the Lagrange multiplier method, we obtain the bound problem of unconditional optimization
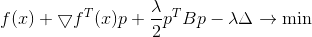
A necessary condition for a minimum for it is
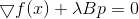, or 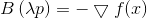from where
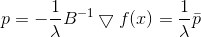
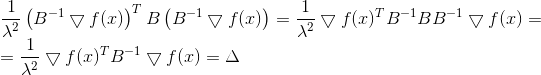
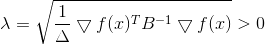
Again we see that the direction
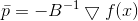, in which we will move, does not depend on the value 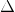- only from the matrix 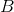. And again, we can either pick up 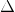that is fraught with the need to calculate 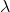and explicit matrix inversion 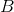, or solve the auxiliary problem of finding a suitable bias 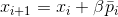. Insofar as 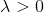, the solution to this auxiliary problem is guaranteed to exist.
So what should it be for matrix B? We restrict ourselves to speculative ideas. If the objective function
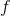- quadratic, that is, it has the form 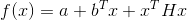where 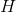positive definite, then it is obvious that the best candidate for the role of the matrix 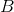is hessian 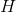, since in this case one iteration of the descent method we have constructed is required. If H is not positive definite, then it cannot be a metric, and the iterations constructed with it are iterations of the damped Newton method, but they are not iterations of the descent method. Finally, we can give a rigorous answer to
Question: Does the Hessian matrix in the Newton method have to be positive definite?
Answer: no, it is not required in either the standard or the damped Newton method. But if this condition is satisfied, then the damped Newton method is a descent method and has the property of global , and not just local convergence.
As an illustration, let’s see what confidence regions look like if the well-known Rosenbrock function is minimized by gradient descent and Newton’s methods, and how the shape of the regions affects the convergence of the process.
This is how the descent method behaves with a spherical confidence region, it is also a gradient descent. Everything is like a textbook - we are stuck in a canyon.
And this we get if the confidence region has the shape of an ellipse defined by the Hessian matrix. This is nothing more than an iteration of the damped Newton method.
The only unresolved question is what to do if the Hessian matrix is not positive definite. There are many options. The first is to score. Maybe you're lucky and Newton's iterations will converge without this property. This is quite real, especially at the final stages of the minimization process, when you are already close enough to a solution. In this case, iterations of the standard Newton method can be used without bothering with the search for a neighborhood admissible for descent. Or use iterations of the damped Newton method in the case of
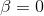, that is, in the case when the obtained direction is not the descent direction, change it, say, to an anti-gradient. Just do not have to explicitly check whether the Hessian is positive definite according to the Sylvester criterion , as was done here !!! . It is wasteful and pointless.
More subtle methods involve constructing a matrix, in a sense close to the Hessian matrix, but possessing the property of positive definiteness, in particular, by correcting eigenvalues. A separate topic is the quasi-Newtonian methods, or variable metric methods, which guarantee the positive definiteness of the matrix B and do not require the calculation of the second derivatives. In general, a detailed discussion of these issues goes well beyond the scope of this article.
Yes, and by the way, it follows from what has been said that the damped Newton method with positive definiteness of the Hessian is a gradient method . Like quasi-Newtonian methods. And many others, based on a separate choice of direction and step size. So contrasting the Newton method with gradient terminology is incorrect.
To summarize
The Newton method, which is often remembered when discussing minimization methods, is usually not the Newton method in its classical sense, but the descent method with the metric specified by the Hessian of the objective function. And yes, it converges globally if the Hessian is everywhere positive definite. This is possible only for convex functions, which are much less common in practice than we would like, so in the general case, without the appropriate modifications, the application of the Newton method (we will not break away from the collective and continue to call it that) does not guarantee the correct result. Training neural networks, even shallow ones, usually leads to non-convex optimization problems with many local minima. And here is a new ambush. Newton's method usually converges (if converges) quickly. I mean very fast. And this, oddly enough, is bad, because we come to a local minimum in several iterations. And it for functions with complex terrain can be much worse than the global one. Gradient descent with linear search converges much more slowly, but is more likely to “skip” the ridges of the target function, which is very important in the early stages of minimization. If you have already well reduced the value of the objective function, and the convergence of the gradient descent has slowed significantly, then here the change in the metric may well accelerate the process, but this is for the final stages.
Of course, this argument is not universal, not indisputable, and in some cases even incorrect. As well as the statement that gradient methods work best in learning problems.
All Articles