Clever Geek Handbook

Data structures for game programmers: bulk data

image






Any programmer will benefit from an understanding of the various data structures and how to analyze their performance. But in practice, I have never come in handy for AVL trees , red-black trees , prefix trees , skip lists , etc. I use some data structures for only one specific algorithm and for nothing more (for example, heaps for implementing a priority queue in the A * path search algorithm ).



In everyday work, I usually do with surprisingly few data structures. Most often, they come in handy for me:





I will devote several articles to how I usually implement all these structures. Let's start with the simplest and most useful - bulk data.



Bulk data



There is no common term for this concept (or I don’t know about it). I call a “ bulk data ” any large collection of similar objects. For example, it could be:





Or, if you are writing code at a higher level of abstraction, it could be:





Typically, each system (rendering, sound, animation, physics, etc.) in a game has a couple of different types of objects that it needs to track. For example, for a sound system it could be:





In the case of bulk data, I will assume the following:





Of course, you can come up with situations in which order is important . For example, if objects denote elements for rendering, then before rendering we may need to sort them from front to back to reduce the amount of redrawing .



However, I believe that in most cases it is preferable to sort the data as it is used , rather than storing the data in a sorted container, such as red-black trees or B-trees . For example, we can sort the rendered objects from front to back before passing them to the renderer, or sort the files alphabetically before displaying them on the screen as a list. Sorting data in each frame may seem costly, but in many cases it is done in O (n) using radix sort .



Since I use only simple data structures, I prefer C ++ objects to C ++ objects, because it’s easier to understand what is happening in memory and evaluate their performance. However, there are situations when you need to store in bulk data something that does not have a fixed size. for example, the name or list of child objects. I will talk about these cases in a separate post, where we look at “arrays of arrays”. For now, let's assume that all objects are simple, fixed-size data structures.



For example, here is what bulk data structures for our hypothetical sound system will look like: 



 typedef struct { resource_t *resource; // Resource manager data uint64_t bytes; // Size of data uint64_t format; // Data format identifier } sound_resource_t; typedef struct { sound_resource_t *resource; // Resource that's playing uint64_t samples_played; // Number of samples played float volume; // Volume of playing sound } playing_sound_t; typedef struct { playing_sound_t *sound; // Faded sound float fade_from; // Volume to fade from float fade_to; // Volume to fade to double fade_from_ts; // Time to start fade double fade_to_ts; // Time to end fade } playing_fade_t;


When considering ways to store bulk data, we need to consider a couple of goals:





The two easiest ways to represent bulk data are a static array or a C ++ vector: 



 // Static array #define MAX_PLAYING_SOUNDS 1024 uint32_t num_playing_sounds; playing_sound_t playing_sounds[MAX_PLAYING_SOUNDS]; // C++ vector std::vector<playing_sound_t> playing_sounds;


Working with an array is extremely simple, and it can work just fine for you if you know exactly how many objects are needed in the application. If you do n't know this , then either waste your memory or you will run out of objects.



The vector std::vector



is also a very worthy and simple solution, but here you need to consider some aspects:





In addition, without additional measures, neither regular arrays nor vectors support references to individual objects. Let's look at this topic, as well as other important design decisions involved in creating the bulk data system.



Removal strategy



The first important decision: what should be done when deleting the object a[i]



. Here are three main options:





The first option is terrible - O (n) is spent on the movement of all these elements. The only benefit of the first method is that if the array is sorted, then the order in it is preserved. But as mentioned above, the order does not bother us. Note that if you use a.erase()



to remove the std::vector



element, this is exactly what will happen!



The second option is often called “swap-and-pop”. Why? Because if you use a C ++ vector, this option is usually implemented by replacing (swapping) the element that you want to delete with the last one, followed by removing or popping the last element: 



 std::swap(a[i], a[a.size() - 1]); a.pop_back();


Why is all this necessary? In C ++, if we assign a[i] = a[n-1]



, we must first remove a[i]



by calling its destructor, and then call the copy constructor to create a copy of a[n-1]



at position i



and finally, we call the destructor a[n-1]



when shifting the vector. If the copy constructor allocates memory and copies data, then this can be pretty bad. If we use std::swap



instead of assignment, then we can do only with the constructors move and should not allocate memory.



Again, that's why C ++ I prefer simple data structures and C operations. C ++ has many performance pitfalls that you can fall into if you don’t know what’s going on inside. In C, swap-erase operation will be very simple: 



 a.data[i] = a.data[--an];


When using swap-and-pop, objects remain tightly packed. To place a new object, simply attach it to the end of the array.



If we use the “with holes” option I, then when placing a new object, we first of all need to check if there are any free “holes” that can be used. It is worth increasing the size of the array only when there are no free "holes". Otherwise, in the process of deleting and creating objects, it will grow indefinitely.



You can use a separate std::vector<uint32_t>



to track hole positions, but there is a better solution that does not require additional memory.



Since the data of the object in the “hole” is not used for anything, you can use it to store a pointer to the next free hole. Thus, all the holes in the array form a simply connected list , and if necessary, we can add and remove elements from it.



This type of data structure, in which unused memory is used to bind free elements, is usually called a free list .



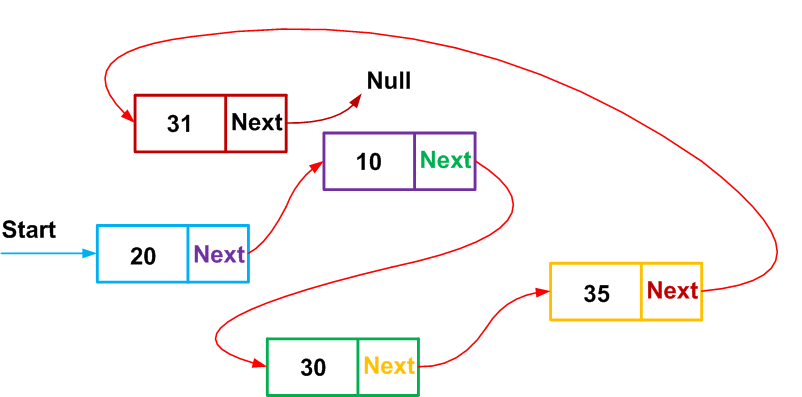
In a traditional linked list, a special list header element points to the first node in the list, and the last list element points to NULL, which means the end of the list. Instead, I prefer to use a circular linked list , in which the heading is just a special list item, and the last list item points to a heading element:









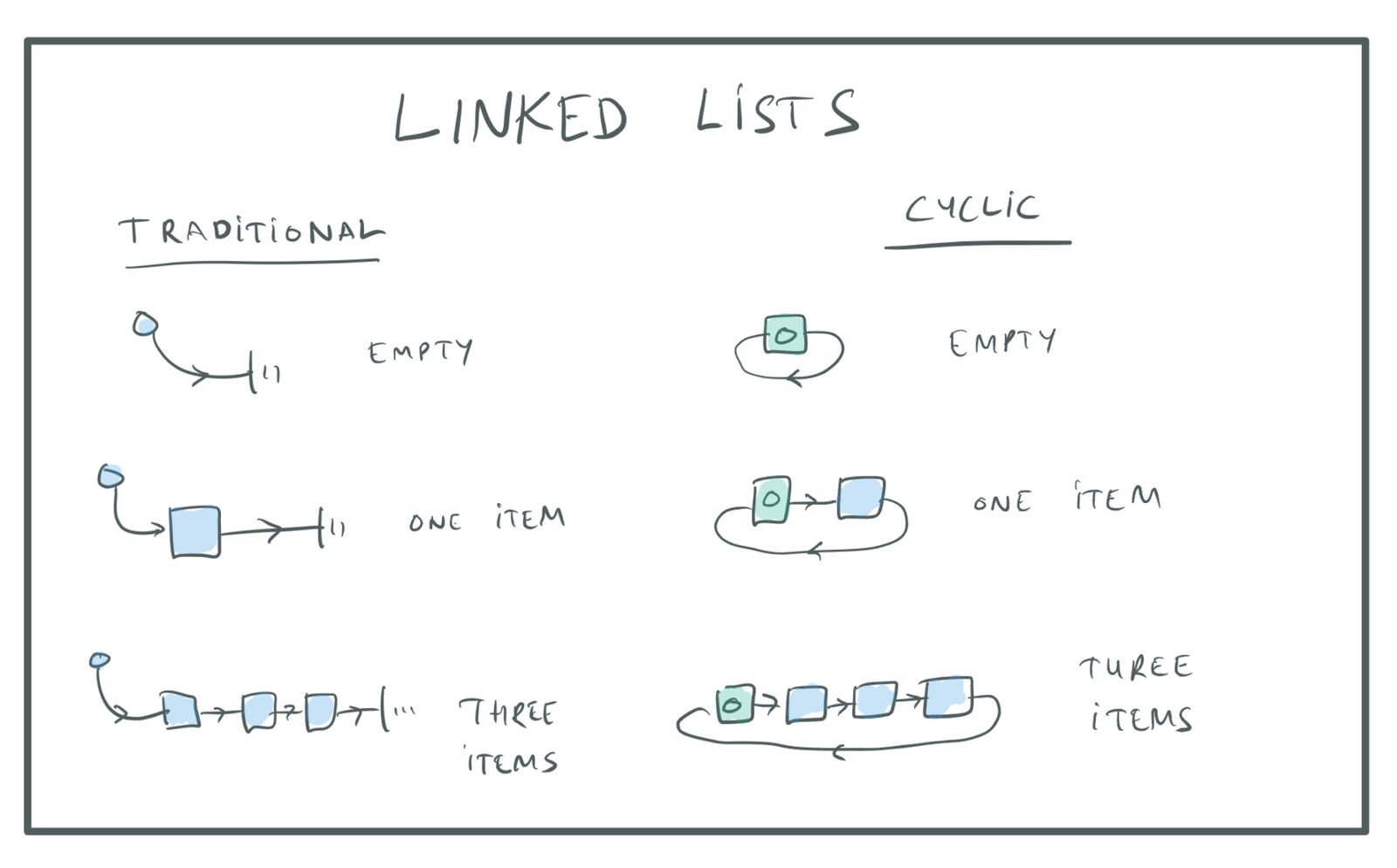
Traditional and ring linked lists.



The advantage of this approach is that the code becomes much simpler by reducing the number of special cases at the beginning and end of the list.



Note that if you use std::vector



to store objects, then pointers to objects will change with every redistribution of the vector. This means that we cannot use regular pointers to a linked list, because pointers are constantly changing. To get around this problem, you can use indexes as "pointers" to a linked list, since the index constantly points to a specific slot even when redistributing the array. We'll talk more about reallocation in the next section.



You can allocate space for a special element of the list title by always storing it in array slot 0.



In this case, the code will look something like this: 



 // The objects that we want to store: typedef struct {...} object_t; // An item in the free list points to the next one. typedef struct { uint32_t next_free; } freelist_item_t; // Each item holds either the object data or the free list pointer. typedef union { object_t; freelist_item_t; } item_t; typedef struct { std::vector<item_t> items; } bulk_data_t; void delete_item(bulk_data_t *bd, uint32_t i) { // Add to the freelist, which is stored in slot 0. bd->items[i].next = bd->items[0].next; bd->items[0].next = i; } uint32_t allocate_slot(bulk_data_t *bd) { const uint32_t slot = bd->items[0].next; bd->items[0].next = bd->items[slot].next; // If the freelist is empty, slot will be 0, because the header // item will point to itself. if (slot) return slot; bd->items.resize(bd->items.size() + 1); return bd->items.size() - 1; }


What is the best removal strategy? Moving the last element to an empty slot, ensuring tight packing of the array or keeping all the elements in their places with the creation of “holes” in the array in place of the deleted element?



When making a decision, two aspects must be taken into account:





Choosing the best option depends on your project.



You can say that storing a densely packed array is better, because iterations over all elements (to update the system) occur more often than matching external links. On the other hand, we can say that the performance of an “array with holes” is worse only in the case of a large number of holes, and in game development we usually care about performance in the worst cases (we want to have a frame rate of 60 Hz, even when the maximum operations are performed in the game) . In the worst case, we have the maximum number of real objects, and in this case there will be no holes in the array. Holes occur only when the number of objects decreases, when we delete some of these objects.



There are also strategies that can be used to speed up the processing of arrays with many holes. For example, we can track the lengths of continuous sequences of holes in order to skip entire sequences of holes at a time, rather than element by element. Since this data is needed only for "holes", and not for ordinary elements, you can store them together with the pointer of the release list in the unallocated memory of objects and not waste extra memory.



In my opinion, if you do not need to optimize the code for fast iterations, then it is probably best to use the "array with holes" option. It is simpler, does not require additional search structures, and you can use the object index as its ID, which is very convenient. In addition, the lack of moving objects eliminates possible bugs.









Bulk data removal strategies.



Weak pointers



As a note, I can say that it is easy to implement support for “weak pointers” or “descriptors” for bulk data objects.



A weak pointer is a reference to an object that can in some way determine that the object to which it refers has been deleted. It is convenient in weak pointers that they allow you to delete objects without worrying about who can refer to them. Without weak pointers to delete an object, we would need to search for each individual link and declare it invalid. This can be especially difficult if the links are stored in script code, on other computers on the network, etc.



Remember that we already have an ID that uniquely identifies existing objects. In the "with holes" option, this ID is simply the index of the element (because the elements never move). In the case of tightly packed arrays, this object index is a record in the search array .



The ID itself cannot be used as a weak pointer, because IDs can be reused. If an element is deleted and a new element is created in the same slot, then we will not be able to figure it out by the ID alone. To get a weak pointer, you need to combine the ID with the generation



field: 



 typedef struct { uint32_t id; uint32_t generation; } weak_pointer_t;


The generation



field is a field in the object's struct that tracks how many times the slot in the bulk data array has been reused. (In the case of tight packing, it keeps track of how many times the slot in the search array has been reused.)



When you delete an item, we increase the generation number in its slot. To check if the weak pointer is still valid, we check if the generation



in the struct of the weak pointer matches the generation of the slot indicated by its id



. If they match, then the source object we are referencing still exists. If not, it means that it is deleted, and the slot is either on the release list or has been reused.



Keep in mind that since the generation



field is necessary for both holes and existing objects, you need to store it outside the union: 



 typedef struct { uint32_t generation; union { object_t; freelist_item_t; }; } item_t;


Distribution strategy



If you use std::vector



to store element data, then when the array is full and needs to be increased, the entire array of elements will be redistributed. Existing elements are copied to the new array.



std::vector



grows geometrically . This means that every time a vector needs to increase, the number of distributed elements is multiplied by some factor (usually by × 2). Geometric (exponential) growth is important because it keeps the costs of increasing the array constant.



When redistributing the array, we need to move all the elements, which requires O (n) . However, as the array grows, we add space for another n elements, because we double the size. This means that we will not need to increase the array again until we add n more elements to it. That is, the increase costs are equal to O (n) , but we only execute them * O (n) * for the nth time of writing to the array, that is, on average, the cost of writing one element is O (n) / O (n) = O (1) .



The cost of recording an item is called the amortized constant , because if you average all the records that are being executed, the costs will be fixed. However, we should not forget that before we average, the costs turn out to be very spasmodic. After every O (n) records we get a peak of height O (n) :









The cost of writing to std::vector



.



Let's also see what happens if we do not use geometric growth. Suppose, instead of doubling the memory during growth, we will simply add another 128 slots. Moving old data still costs us O (n) , but now we need to do it every 128 items we add, that is, the average costs will now be O (n) / O (128) = O (n) . The cost of writing an element to an array is proportional to the size of the array, so when the array becomes large, it starts working at a turtle speed. Oops!



The std::vector



distribution strategy is a good standard option, working well in most cases, but it has some problems:





The code below is an example of bugs that can occur when moving objects: 



 // Create two items and return the sum of their costs. float f(bulk_data_t *bd) { const uint32_t slot_1 = allocate_slot(bd); item_t *item_1 = &bd->items[slot_1]; const uint32_t slot_2 = allocate_slot(bd); item_t *item_2 = &bd->items[slot_2]; return item_1->cost + item_2->cost; }


The problem here is that the allocate_slot()



function might need to redistribute the array to create space for item_2



. In this case, item_1



will be moved to memory and the pointer to item_1



will cease to be valid. In this specific case, we can eliminate the error by moving the assignment item_1



, but similar bugs can appear more imperceptibly. Personally, they have bitten me many times.



Such a situation is perfidious by the fact that the bug will crawl out only when the array is redistributed exactly at the moment slot_2



. The program can work correctly for a long time until something changes the distribution pattern, after which the bug will work.



All these problems can be solved using a different distribution strategy. Here are some of the options:





I repeat, each method has its own advantages and disadvantages. The latter is good because the elements are still stored in memory next to each other, and we need to track a single buffer, so additional vectors or lists are not required. It requires setting the maximum size of the array, but the space of virtual addresses is so large that you can usually specify any huge number without the slightest problem.



If you cannot use a solution with virtual memory, then which approach would be better - fixed size or blocks with geometric growth? If the array is very small, then a fixed size spends a lot of extra memory. For example, if a block has a size of 16 thousand elements, then you use all these 16 thousand elements, even if there is only one element in the array. On the other hand, with geometric growth, you will be wasting memory with a very large array, because on average the last distributed block will be 50% full. For a large array, this can be many megabytes.



Once again I will say that in the development of games it is more important to optimize the code for the worst case, so I'm not really worried about wasting memory on small arrays, if large arrays always show good performance. The total amount of wasted memory will never be more than * 16 K * n *, where n is the number of separate bulk data arrays in the project, and I do not think that we will have many different arrays (only a few pieces for each system).



Fixed-sized blocks have two other advantages. Firstly, calculations to find an element by its index are simpler, this is just blocks\[i / elements_per_block\][i % elements_per_block]



. Secondly, allocating memory directly from virtual memory is much more efficient than accessing a dynamic allocator (heap allocator) due to the lack of fragmentation.



In conclusion, I want to say that if you use the “with holes” option for data storage, then in my opinion it is worth moving away from the distribution strategy through std::vector



so that objects receive constant pointers that never change. Most likely, a large array of virtual memory will be the best solution, but if you cannot implement it, then the second best option is a sequence of blocks of a fixed size.



Note that since this approach makes pointers to objects permanent, now in addition to IDs, we can use pointers to objects to refer to objects. The advantage of this is that we can access objects directly, without performing index searches. On the other hand, a pointer needs 64 bits of memory, and 32 bits are usually enough for an index (4 billion objects is a lot).









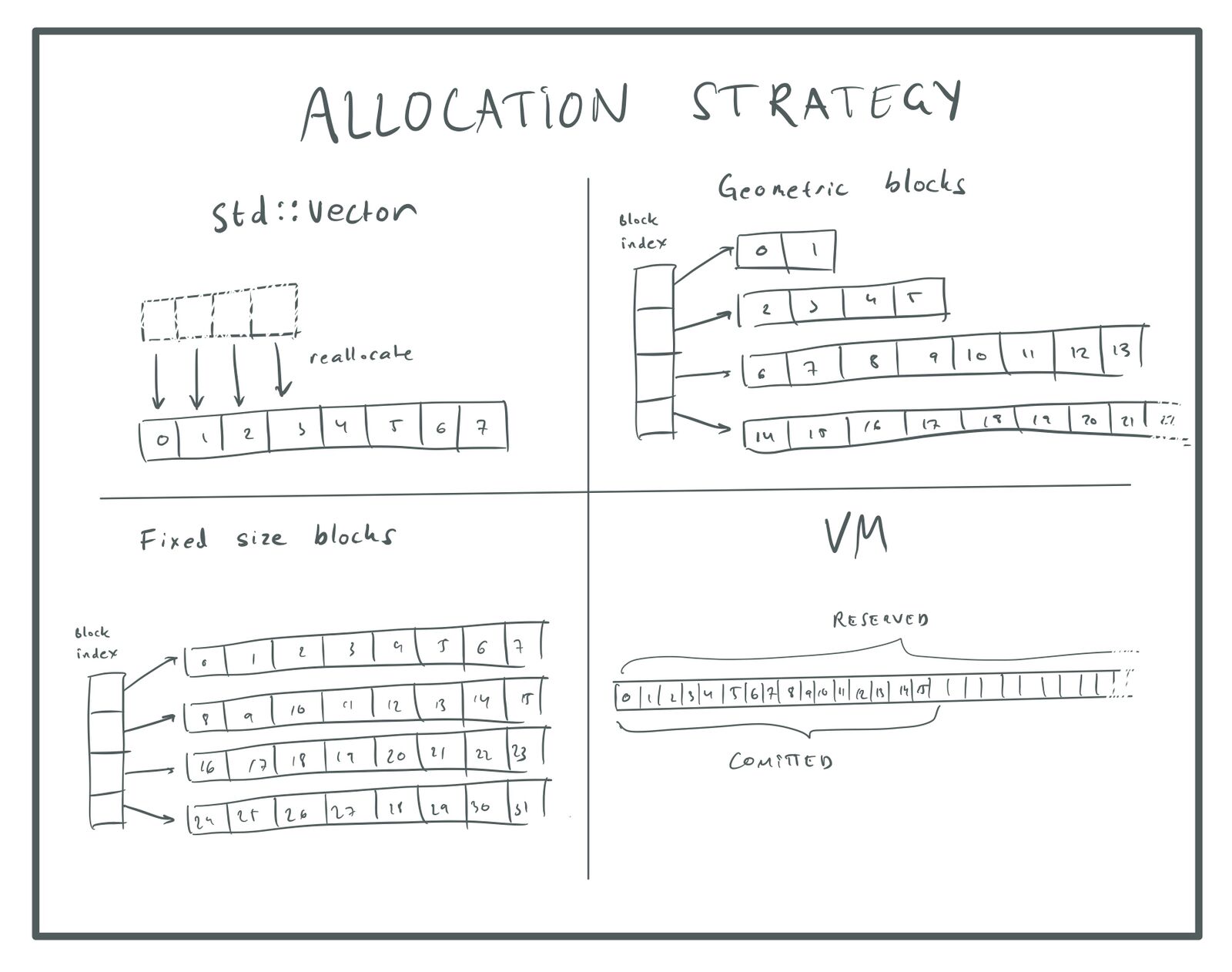
Distribution strategies



Array of structures and array structure



Another important design decision is to choose between an array of structures (Array of Structures, AoS) and an array structure (Structure of Arrays, SoA). The difference is best shown by example. Suppose we have one particle system in which the particles have a lifetime, position, speed and color: 



 typedef struct { float t; vec3_t pos; vec3_t vel; vec3_t col; } particle_t;


The usual way to store it would be to put many of these struct into an array. That is why we call it an “array of structures”. I.e: 



 uint32_t num_particles; particle_t *particles;


Of course, instead of the usual array, you can use any of the above strategies.



In the array structure (SoA) variant, we use a separate array for each struct field: 



 uint32_t num_particles; typedef struct { float *t; vec3_t *pos; vec3_t *vel; vec3_t *col; } particles;


In fact, we can go even further, because vec3_t



in itself is a struct: 



 uint32_t num_particles; typedef struct { float *t; float *pos_x; float *pos_y; float *pos_z; float *vel_x; float *vel_y; float *vel_z; float *col_r; float *col_g; float *col_b; } particles;


This seems a lot more complicated than our original AoS scheme, so why is it really necessary? There are two arguments in support of this approach:





Does this mean that with these accelerations it tick()



will become 80 faster? No.We will get the first acceleration of 10 times only if we are completely limited by memory, and if we are completely limited by memory, SIMD will not be able to let us work faster.



Disadvantages of the SoA approach:





As an example of what kind of problems can arise with the cache, recall the struct particles shown above and imagine that we allocated all arrays using a VM (that is, they are aligned on the borders of a four-kilobyte page). Because of this alignment, all 10 fields of the struct particles will be bound to one cache block. If the cache is 8-channel multiple-associative, then this means that all the fields of the particle cannot be in the cache at the same time. Oops!



One way to solve this problem is to group the particles by the size of the SIMD vector. For example, we can do the following: 



 uint32_t num_particles; typedef struct { float t[8]; float position_x[8]; float position_y[8]; float position_z[8]; float velocity_x[8]; float velocity_y[8]; float velocity_z[8]; float color_r[8]; float color_g[8]; float color_b[8]; } eight_particles_t; eight_particles_t *particles;


In this scheme, we can still use the SIMD instructions to process eight particles at a time, but the fields of one particle are pretty close in memory and we have no problems with cache line collisions that appeared earlier. This is better for a distribution system, because we are back to one distribution per whole array of particles.



In this case, the algorithm tick()



will affect 32 bytes, skip 288 bytes, affect 32 bytes, etc. This means that we will not get full 10x acceleration, as in the case of a separate arrayt



. Firstly, cache lines usually have a size of 64 bytes, and since we use only half, we cannot accelerate more than 5 times. Also, the costs associated with skipping bytes may occur, even if we process the full cache lines, but I'm not 100% sure about this.



To solve this problem, you can experiment with the size of the group. For example, you can resize a group [16]



to one float field that fills the entire cache line. Or, if you use a block allocation method, you can simply set the size of the group to any value that fits into the block:









AoS and SoA.



As for the deletion strategy, SoA is not the best choice for the “with holes” option, because if we use SIMD to process eight elements at the same time, we won’t be able to miss holes in any way (unless all eight elements are “holes”) .



Since SIMD instructions process “holes” in the same way as real data, we need to ensure that holes contain “safe” data. For example, we don’t want hole operations to cause exceptions in floating point operations or to create subnormal numbers that reduce performance. Also, we should no longer keep the pointernext



a release list using union because SIMD operations will overwrite it. Instead, use the struct field.



If we use the densely packed option, then deleting will be a bit more expensive, because you have to move each field individually, and not the whole struct at a time. But since the removal is much more difficult than the updates, this will not be a big problem.



Comparing AoS and SoA, I can say that in most cases, improving performance is not worth the hassle of writing more cumbersome code. I would use it as the “standard” storage format for AoS systems and switch to SoA for systems that require SIMD computing speeds, such as clipping systems and particles. In such cases, for maximum speed, I would probably choose densely packed arrays.



It is worth considering another option - storing data in AoS and generating temporary SoA data for processing by some algorithm. For example, I would do one pass on AoS data and write them to a temporary SoA buffer, process this buffer, and then write the results back as AoS (if necessary). Since in this case I know for sure the algorithm that will process this data, I can optimize the storage format for it.



Keep in mind that this approach works well with the “block storage” option. You can process one 16 thousandth block at a time, convert it to SoA, execute the algorithm, and write the results back. To store temporary data, you only need a scratch buffer with 16 thousand elements.



Conclusion



Any approach has its advantages and disadvantages, but “by default” I recommend storing bulk data for the new system as follows:



An array of structures with “holes” and constant pointers, either distributed as one large reserved volume in the VM (if possible), or as an array of blocks of a fixed size (16 thousand each or in a size that is optimal for your data).


For cases when you need very fast calculations of values ​​for data:



The structure of arrays of tightly packed objects, grouped by 8 for SIMD processing and distributed as one large reserved volume in a VM or as an array of blocks of a fixed size.


Next time we will consider the topic of indexing this data.


More articles:


All Articles