How to make a BTC transaction without depositing small coins

Many bitcoin wallets when choosing coins to send prefer to use a large coin, the balance of which is greater than the amount sent. After each such transaction, a change coin is formed. After some time, the entire wallet is overgrown with such coins of the order of 0.001 (~ $ 10 at the moment), which there is already nothing to spend on. When, once again, I needed to make a transaction, it occurred to me whether it was possible to assemble a transaction so that there was no change. The wallet stubbornly offered to "cut" another larger coin, so I decided to pick coins with my hands in order to collect the necessary amount. However, this turned out to be not so simple: the sum either turned out to be less than the desired value or exceeded it too much. As a result, I decided that there should be an algorithm with which you can collect the desired amount from coins or a little more. It turned out that this is not only possible, but works so well that made me write this article. But first things first.

Backpack problem

The backpack problem is widely known: to pack as many valuable things as possible into a backpack, provided that the capacity of the backpack is limited. In this case, we have the case of the 0-1 backpack problem , since each item (coin) is available for packing in the backpack only once. In addition, the weight of each “item” coincides with its value, so we are dealing with an even more special case, the problem of the sum of the subsets . Wikipedia suggests using a genetic algorithm, but I decided to look for an exact solution using dynamic programming, as this is quite achievable in terms of resources and looks simple.

To reduce the problem of choosing coins to the task of a backpack, you need to make a small conversion of the input data. The fact is that solving the knapsack problem (more precisely, the sum of the subsets) will give us a subset of the original set that has a maximum sum that does not exceed the parameter (backpack carrying capacity). But we are not satisfied with the combination of coins, giving the amount less than the amount that we want to send. However, we are comfortable with combinations that are slightly superior. For example, if we need to send 0.005 bitcoins, and we found a combination that gives 0.00499, then it is useless to us, since it is less than the amount that the seller wants. But if we find 0.005001, that’s right. Extra satoshiki can be used as a commission (we will talk about it in detail below) or give the seller if he allows sending a larger amount. Therefore, with the help of the backpack problem, we need to choose not those coins that need to be sent , but those that need to be left . Then the "shortage" to the maximum will turn into "bust" in terms of the original problem.

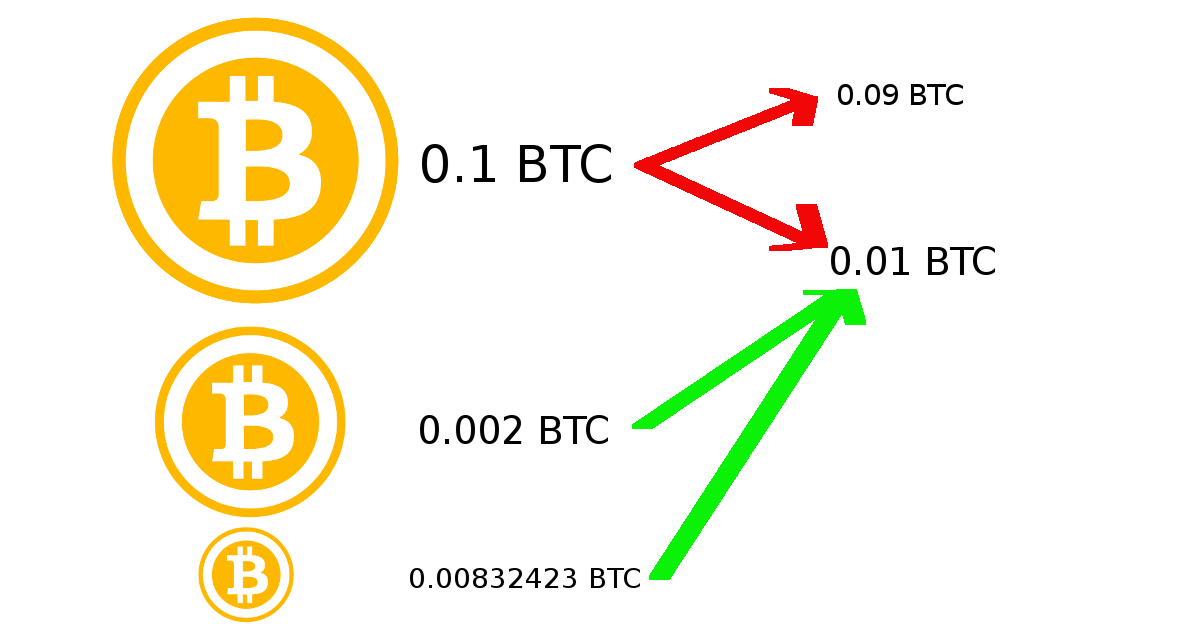
Example. Let's say we have such coins: 0.1 BTC, 0.002 BTC, 0.00832423 BTC. And we need to send 0.01 BTC. Let us find such coins, the sum of which will be maximum, but less than or equal to the total amount of our coins minus the amount sent, that is, such a number: 0.1 + 0.002 + 0.00832423 - 0.01 = 0.10032423. In this case, a simple search finds that it is a 0.1 coin. We leave it, which means we send the rest: 0.002 BTC and 0.00832423 BTC, which in total give 0.01032423 BTC, which is more than 0.01 BTC and suits us. (True, the commission came out about $ 3, but let's say that the network is busy and we want to make the sending as fast as possible.)

Commissions

To take into account transaction fees, I modified each input coin, reducing its balance by the amount that would have to be paid for its inclusion in the transaction as an input. This can be done by knowing the size of the input and the commission (for example, 2 satoshi per byte). In addition, I modified the amount sent, adding to it the price of the part of the transaction that does not depend on the selected coins: header and exit (s). The user can specify all of these parameters using flags. You can also disable the adjustment for commissions in general by specifying a commission of 0 Satoshi per byte.

I took information on the sizes of inputs and outputs in different versions of addresses (classic, wrapped segwit and native segwit from here: https://bitcoin.stackexchange.com/a/84006

Algorithms and implementation

I immediately dropped the genetic algorithm, maybe in vain. Focused on accurate algorithms. My first attempt was to realize through exhaustive search of all combinations, but even on 40 coins he worked for hours and had to abandon it. Then I tried the dynamic programming suggested on Wikipedia . In it, you can not keep in memory the entire matrix, but only the current and previous rows. In addition, we do not need to store the value, since it coincides with the weight and is the column number. But we need to remember the combination - I decided to store it in the form of a bitset. In addition, you can store only one row, building the next row in-place from it. Each nonzero row record remains in its place and is copied (with the addition of the corresponding bit) to another cell a certain number of cells to the right (if it was empty before). If you go in the reverse order, sorting through the cell into which the "jump" goes, then you can fill everything correctly:

Each nonzero cell in the current row generates in the next row itself and another cell for a certain number of cells (equal to the value of the added coin) to the right. If there is already a value in that cell, then the option with the largest number of selected (that is, not included in the transaction) coins “wins”, since we want to send as few coins as possible, other things being equal.

On one cell I spend 8 bytes for a bitset, and the number of cells is equal to the possible number of balances from 0 to the amount of coins minus the amount sent. For example, if there is only 1 bitcoin in the wallet, and 0.1 is sent, then there will be 100'000'000-10'000'000 = 90'000'000 cells, each of 8 bytes, that is 720 megabytes - a little for a modern computer. If the number of coins is less than 32, then 4 bytes per coin could be used, but I did not optimize it. In addition, if there are more than 64 coins, then the program does not work - this would also have to be fixed by making a bitset of arbitrary length. Finally, you can discard the last sign in the balances, losing a little accuracy, but winning 10 times in memory. But so far it will do.

I called the program changeless and placed it on the gitlab: gitlab.com/starius/changeless . It is written in Go, assembled using go get



, as usual. Available binaries for Linux, Windows, Mac , collected in CI.

When I launched the program with real coins, I was amazed at how accurately she picked up the necessary combination. When the number of coins is large, almost any amount commensurate with the balance of the coins can be selected with accuracy down to satoshi! You change the required amount for 1 satoshi and the program gives a completely different combination of coins exactly for this amount. Below is an example of working on 50 random coins with balances from 0 to 1 bitcoin.

 $ cat coins50.txt 0.01331611 0.03906237 0.04847086 0.08453118 0.09748168 0.10395389 0.10619825 0.12156721 0.12923149 0.13587973 0.14798976 0.16053788 0.19011834 0.21570038 0.21946913 0.31861430 0.33435508 0.33718842 0.33789473 0.35976748 0.37360122 0.44944553 0.47572926 0.49927495 0.50992142 0.53062326 0.53079433 0.53542072 0.54715225 0.55019714 0.55313907 0.56656642 0.56673333 0.65879650 0.66228482 0.68424322 0.70436496 0.75638055 0.79095597 0.82438005 0.83684407 0.85151564 0.86862948 0.90054250 0.90239402 0.91636213 0.93087757 0.93579251 0.97207439 0.98248384 $ changeless -amount 10.00000000 -coins coins50.txt Processing item 50/50. 0.09748168 + 0.33435508 + 0.47572926 + 0.53542072 + 0.66228482 + 0.70436496 + 0.75638055 + 0.82438005 + 0.9005425 + 0.90239402 + 0.91636213 + 0.93579251 + 0.97207439 + 0.98248384 = 10.00004651 Tx size: 2118 vBytes. Total fees: 0.00004651 BTC (2.2 sats/vByte). $ changeless -amount 10.00000001 -coins coins50.txt Processing item 50/50. 0.01331611 + 0.09748168 + 0.53079433 + 0.56656642 + 0.70436496 + 0.75638055 + 0.82438005 + 0.86862948 + 0.9005425 + 0.91636213 + 0.93087757 + 0.93579251 + 0.97207439 + 0.98248384 = 10.00004652 Tx size: 2118 vBytes. Total fees: 0.00004651 BTC (2.2 sats/vByte).
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

The program managed to pick up combinations of coins to send exactly 10 bitcoins and exactly 10.00000001 bitcoins (10 bitcoins and 1 satoshi). To see this, you must subtract the commission from the amount of coins: 10.00004651 - 0.00004651 = 10, 10.00004652 - 0.00004651 = 10.00000001.

How to get a list of coin balances

For the Electrum program, I found this way (console command):

 ' '.join((x["value"]) for x in listunspent())
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

If you want to exclude certain coins, for example at a certain address, then this can be done like this:

 ' '.join((x["value"]) for x in listunspent() if x["address"] != "bad address")
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

For other wallets, I did not find such an easy way and had to retype it with my hands.