How to invert three signals with two inverters or their role in the history of computers

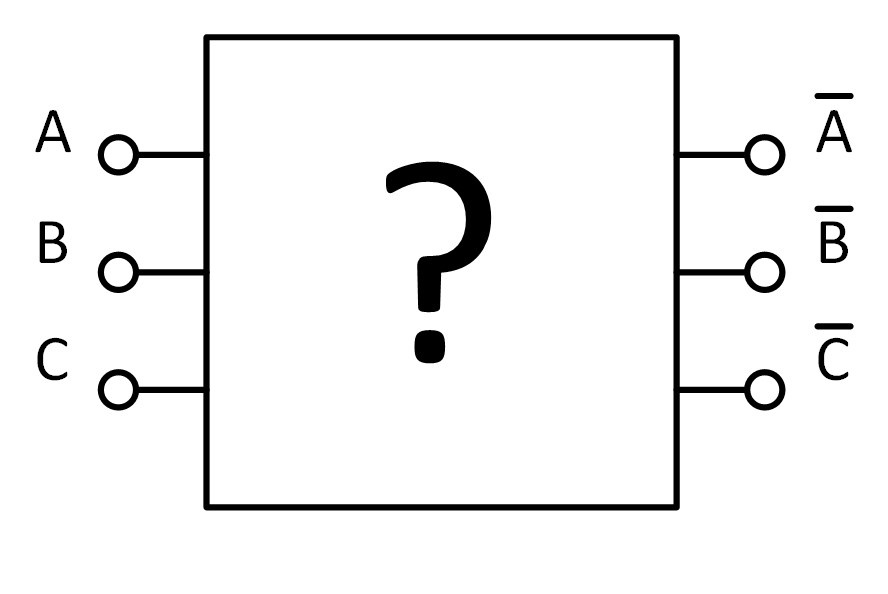Task “Is it possible to invert three signals if you have only two inverters and an unlimited number of“ AND ”and“ OR ”elements? we decided at the institute for one pair. Now her decision baffles even advanced professionals. Let's see how the geektimes-community will cope with it, and at the same time I will try to restore the history of its occurrence ...



A teacher at the institute told me that such problems arose in the era of lamp computers. But we did not have enough minds to ask the details of our students, because now we have to restore the history from the description of the old machines and think a little.

The first electronic computers were built on lamps. So, the first in the USSR (1950) MESM computer contained about 6000 lamps, with the help of which the logical functions "AND", "OR" and "NOT" of binary logic were implemented, which are the basis of modern computers. The implementation of the classic valves on the lamps can be viewed in the picture.







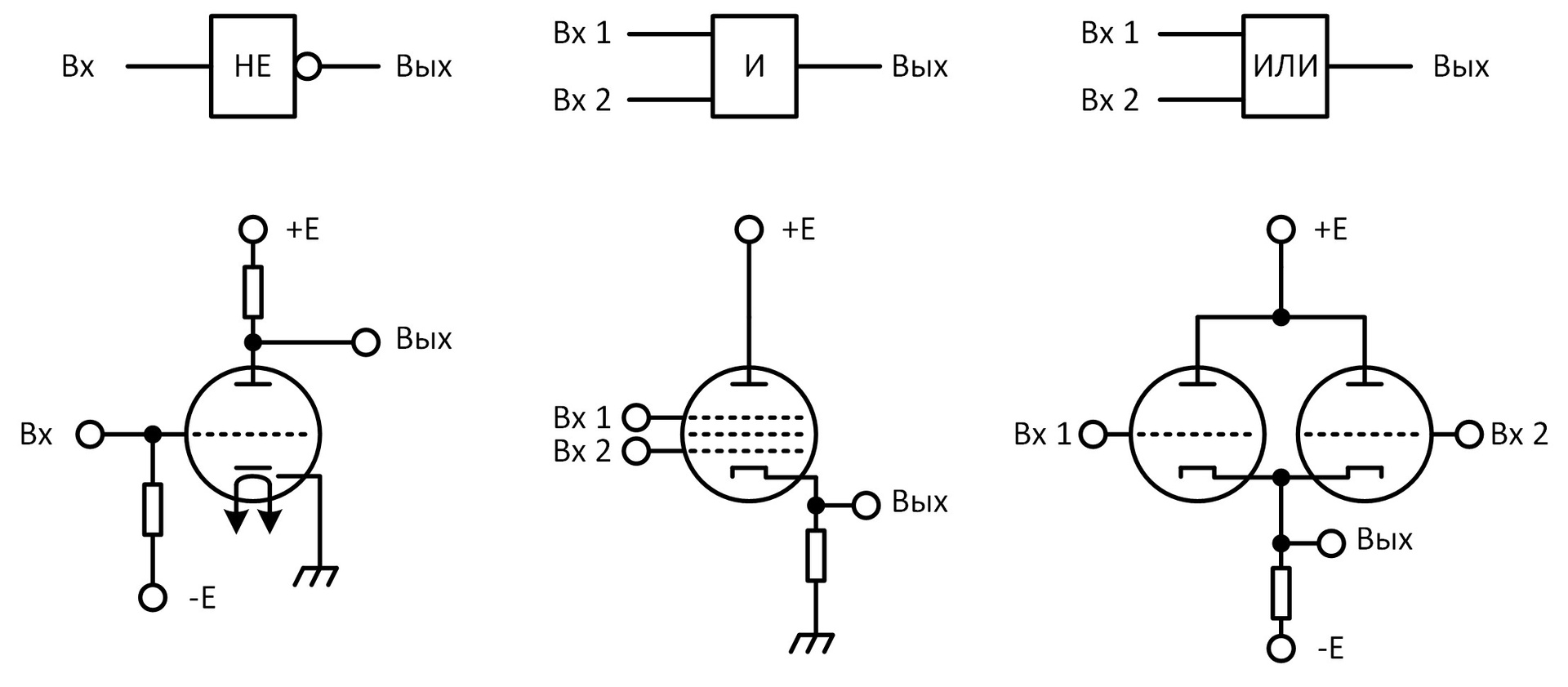
The logical function "And" was built on a single lamp, the number of inputs was determined by the number of grids in the lamp. And for the implementation of the element of the classic valve "2ILI" two lamps were required. And although later the so-called compactrons appeared, something like the assemblies of several lamps in one flask, the engineers still had to optimize logical expressions for the “AND” function to prevail in them. The lamps were expensive, not reliable (750 hours), emit a lot of heat, but most importantly they were huge. In 1952, the first domestic semiconductor diodes appeared to replace low-power lamps. Their appearance marked the emergence of diode logic, which significantly reduced the size of the logic gates. The implementation of the function “AND” and “OR” on diode logic is shown in the figure.







But for the implementation of the inverter still needed a lamp. Semiconductor diodes have already been used to build the BESM-2 machine, and it already contained 4,000 lamps and 5,000 semiconductor diodes. Reducing the size and consumption of the "And" and "OR" valves was significant, and forced to optimize logic functions to reduce the number of inverters in the circuit. Probably it was then that the engineers had to solve this problem for the first time.

The serial production of transistors, which allowed completely to abandon the lamps, began in our country in 1955. And in 1959, the first transistorless tubeless computer was the “Setun” machine, although it still had 20 lamps.



And still back to our problem.



If anyone knows the solution, let's not spoil the pleasure of those who want to solve it themselves. Answers are accepted in the comments, please arrange them as a record in C or Verilog.

Option {nA, nB, nC} <=! {A, B, C}; not accepted, these are three inverters.



UPD: