科学界では、データの視覚化と理論設計が非常に重要な役割を果たします。 MarkdownやMathJaxなどのLaTeXコマンドを実装するツールは、数式の便利で美しい表示によく使用されます。

Juliaには、 LaTeXの構文を使用できるパッケージのセットもあり、シンボリック代数の手段と組み合わせて、数式を処理するための強力なツールを取得します。

今日必要なものをすべてダウンロードして接続する

using Pkg Pkg.add("Latexify") Pkg.add("LaTeXStrings") Pkg.add("SymEngine") using Latexify, LaTeXStrings, Plots, SymEngine
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

LaTeXStrings

LaTeXStringsは、 Julia文字列リテラルにLaTeX方程式を簡単に入力できるようにする小さなパッケージです。 Juliaで通常の文字列を使用してLaTeX方程式が埋め込まれた文字列リテラルを入力する場合、すべてのバックスラッシュとドル記号を手動で回避する必要があります。たとえば、 $ \alpha^2 $



は\$\\alpha^2\$



と記述されます。 さらに、IJuliaは（ MathJaxを介して）LaTeX形式の方程式を表示できますが、これは通常の行では機能しません。 したがって、LaTeXStringsパッケージは以下を定義します。

• LaTeXString
  
  
  
  クラス（ String
  
  
  
  サブタイプ）は、文字列のように機能します（インデックス作成、変換など）が、IJuliaではテキスト/ラテックスとして自動的に表示されます。
• 文字列マクロL"..."
  
  
  
  およびL"""..."""
  
  
  
  、バックスラッシュとドル記号をエスケープせずにLaTeX方程式を入力できるようにします（省略した場合はドル記号を追加します）。

 S = L"1 + \alpha^2"
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

REPLは次を出力します 。

 "\$1 + \\alpha^2\$"
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Jupyterは以下を表示します：

$$

$$1 + \ alpha ^ 2$$

インデックスは通常の行のように機能します。

 S[4:7] "+ \\a"
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

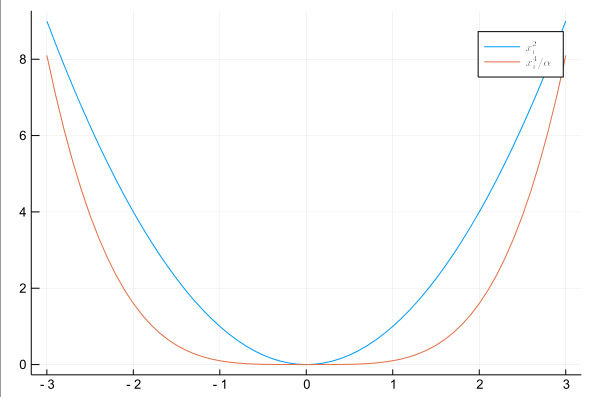
このような線は、グラフの設計に役立ちます。

 x = [-3:0.1:3...] y1 = x .^2 α = 10 y2 = x .^4 / α; plot(x,y1, lab = "\$x^2_i\$") plot!(x,y2, lab = L"x^4_i/\alpha")
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ラテックス化

より機能的なパッケージはLatexify （ Guide ）です。 juliaオブジェクトからLaTeX数学を生成するように設計されています。 このパッケージは、ジュリアの相同性を使用して、式をLaTeX形式の文字列に変換します。 Latexify.jlは、次のようなさまざまなJuliaオブジェクトを変換するための関数を提供します。

• 表現
• 行
• 数値（有理数と複素数を含む）、
• SymEngine.jlのシンボリック式、
• DifferentialEquations.jlのParameterizedFunctionsおよびReactionNetworks
  
  サポートされているすべてのタイプの配列と同様に。

 ex = :(x/(y+x)^2) #  latexify(ex)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$

$$\ frac {x} {\ left（y + x \ right）^ {2}}$$

 str = "x/(2*k_1+x^2)" #  latexify(str)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$

$$\ frac {x} {2 \ cdot k_ {1} + x ^ {2}}$$

異種要素の配列：

 m = [2//3 "e^(-c*t)" 1+3im; :(x/(x+k_1)) "gamma(n)" :(log10(x))] latexify(m)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$

$$\ left [\ begin {array} {ccc} \ frac {2} {3}＆e ^ {-c \ cdot t}＆1 + 3 \ textit {i} \\ \ frac {x} {x + k_ {1}}＆\ガンマ\左（n \右）＆\ log_ {10} \左（x \右）\\ \ end {array} \右]$$

数式を表示し、Habrが理解できる形式でバッファーにコピーする関数を指定できます。

 function habr(formula) l = latexify(formula) res = "\$\$display\$$l\$display\$\$\n" clipboard(res) return l end habr(ex)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$

$$\ frac {x} {\ left（y + x \ right）^ {2}}$$

 <p>$<!-- math>$$display$$\frac{x}{\left( y + x \right)^{2}}$$display$$</math -->$</p>
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

覚えておいてください

 latexify("x/y") |> display
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$

$$\ frac {x} {y}$$

 latexify("x/y") |> print
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$\frac{x}{y}$

Symengine

SymEngineは、Latexifyを使用してJupyterで視覚化できるシンボリック計算を提供するパッケージです。

行と引用符で文字を指定できます（ quote



）：

 julia> a=symbols(:a); b=symbols(:b) b julia> a,b = symbols("ab") (a, b) julia> @vars ab (a, b)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

マトリックスを定義して美しく表示する

 u = [symbols("u_$i$j") for i in 1:3, j in 1:3] 3×3 Array{Basic,2}: u_11 u_12 u_13 u_21 u_22 u_23 u_31 u_32 u_33 u |> habr
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$

$$\ left [\ begin {array} {ccc} u_ {11}＆u_ {12}＆u_ {13} \\ u_ {21}＆u_ {22}＆u_ {23} \\ u_ {31}＆u_ {32}＆u_ {33} \\ \ end {array} \ right]$$

ベクトルがあるとします

 C = symbols("Ω_b/Ω_l") J = [symbols("J_$i") for i in ['x','y','z'] ] h = [0, 0, symbols("h_z")] 3-element Array{Basic,1}: 0 0 h_z
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ベクトル乗算する必要があります

 using LinearAlgebra × = cross latexify(J×h, transpose = true)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$ $$ display $$ \ begin {equation} \ left [\ begin {array} {c} J_ {y} \ cdot h_ {z} \\-J_ {x} \ cdot h_ {z} \\ 0 \\ \ end {array} \ right] \ end {equation} $$表示$$

完全なマトリックス計算：

 dJ = C*(u*J.^3)×h latexify( dJ, transpose = true) habr(ans)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$ $$ display $$ \ begin {equation} \ left [\ begin {array} {c} \ frac {h_ {z} \ cdot \ left（u_ {21} \ cdot J_ {x} ^ {3} + u_ { 22} \ cdot J_ {y} ^ {3} + u_ {23} \ cdot J_ {z} ^ {3} \右）\ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ \ frac { -h_ {z} \ cdot \ left（u_ {11} \ cdot J_ {x} ^ {3} + u_ {12} \ cdot J_ {y} ^ {3} + u_ {13} \ cdot J_ {z} ^ {3} \右）\ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ 0 \\ \ end {array} \ right] \ end {equation} $$ display $$

ここでは、このような単純なチェーンを使用して、行列式を見つけてHabrに送信できます。

 u |> det |> habr
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$

$$u_ {11} \ cdot \ left（u_ {22}-\ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right）\ cdot \ left（u_ {33}-\ frac {u_ {13} \ cdot u_ {31}} {u_ {11}}-\ frac {\ left（u_ {23}-\ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \右）\ cdot \左（u_ {32}-\ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \右）} {u_ {22}-\ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \右）$$

再帰的！ 逆行列はおそらく同様の方法で計算されます：

 u^-1 |> habr
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ブラウザでMatjaxを傷つけたい場合は、マイナス2次（逆行列の2乗）を入れます

ところで、SymEngineは派生物を考慮します：

 dJ[1] |> habr
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$

$$\ frac {h_ {z} \ cdot \ left（u_ {21} \ cdot J_ {x} ^ {3} + u_ {22} \ cdot J_ {y} ^ {3} + u_ {23} \ cdot J_ {z} ^ {3} \右）\ cdot \ Omega_ {b}} {\ Omega_ {l}}$$

 diff(dJ[1], J[1]) |> habr
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$

$$\ frac {3 \ cdot J_ {x} ^ {2} \ cdot h_ {z} \ cdot u_ {21} \ cdot \ Omega_ {b}} {\ Omega_ {l}}$$

ちなみに、ジュリアは数式だけでなく、LaTeX 'aのグラフィックも使用できます。 また、 MikTexをインストールしてpgfplotsを既にダウンロードしている場合は、適切な環境を使用して、ジュリアと友達になれます。これにより、ヒストグラム、3次元グラフ、エラーのある輪郭を作成し、LaTeXドキュメントに統合することができます。

それはすべて数式であり、シンボリック計算ではありません。ジュリアには、シンボリック代数のより複雑で興味深い解決策がまだあります。