- 1つの擬似乱数との比較(異なる方法で取得することもできます[ 1 ]);
- 2つの擬似乱数の最大または最小と比較します。
- 2つ以上の乱数の平均を比較する(平均も異なると見なすことができます)。
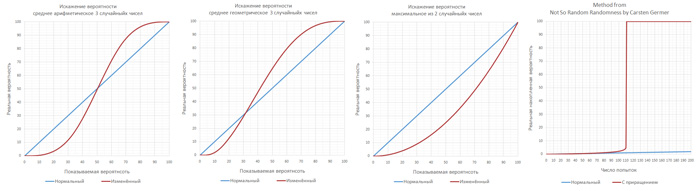
精度ボーナスはさまざまな方法で実装できるため、さまざまな理由でプレイヤーを苛立たせます。
同様に、行われたダメージは、特にサイコロ(キューブ)に基づいて異なる方法で計算できます。
これらの異なるアプローチはすべて、ゲームプレイに影響を与えます。その複雑さと予測可能性です。 それらのそれぞれは、追求された目標に応じて良い決定であることが判明する可能性があるため、意識的に選択することが最も有益です。
この記事では、さまざまなアプローチでの実際の確率の変化の視覚的なグラフを提示します。これにより、彼らは迅速にナビゲートし、より良い決定を下すことができます。
精度の操作
通常、プレイヤーはキャラクターの精度が60%であると通知されると、この情報を「10ショットのうち6ヒットを数えることができる」と認識します。 そして、10回のヒットのうち、6回ではなく1回のヒットを観測する場合、彼はほぼ確実にゲーム内の事故が壊れていると見なします。 これが100ショットのセグメントで発生する場合、彼は特にこれを確信します。 このようなトラブルを回避するために、開発者はヒットの本当の確率を密かに操作します( またはランダム性の要素を放棄します )。
たとえば、Fire Emblem:The Binding Bladeというゲームでは、ヒットを正確に判断するために、1つの乱数ではなく2つの乱数の平均が比較されました[ 2 ]。
この操作の結果、適切に狙われた攻撃(> 50%)が均一な分布で行われるよりもはるかに頻繁に落下し、激しい攻撃(<50%)はあまり一般的ではありません。 この確率分布の変化は次のとおりです。
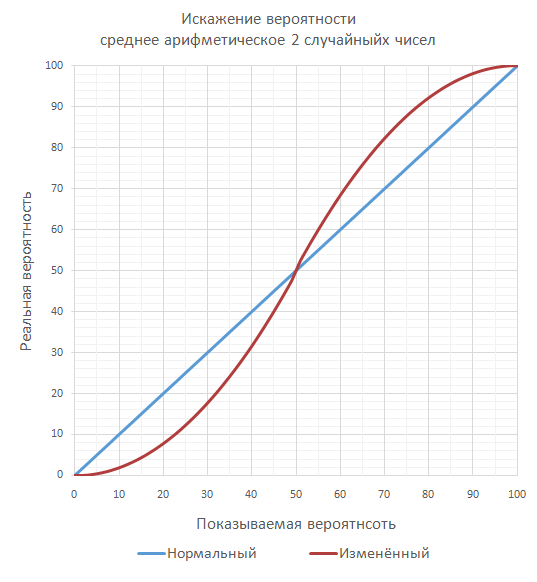
たとえば、示された精度の10%で、実際の精度は1.9%です。 そして75%で、実際は87.24%になります。
ただし、その点については、他の多くの方法で精度を変更できます。
たとえば、3つの乱数の平均を取ることができます。
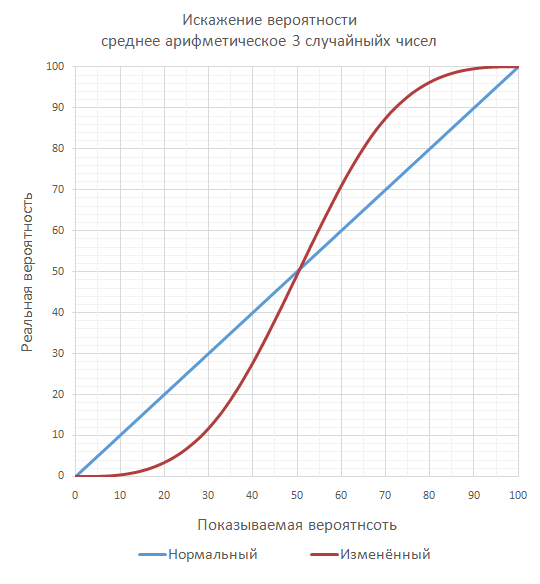
この結果、歪みはさらに顕著になります。10%の精度は0.41%になります。 75%の精度は92.69%になります。
ただし、平均は幾何平均として計算することもできます。 2つの乱数の幾何平均による変化は次のとおりです。
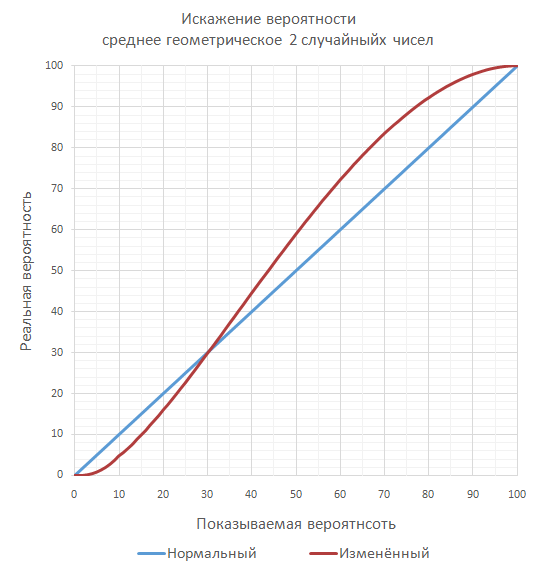
ここでは、10%が4.83%に、75%が88.18%になります。 しかし、最も興味深いことに、遷移は算術平均として50%ではなく30%で発生します。 したがって、プレイヤーが常にアドバンテージを持っていることを確認したい場合は、プレイヤーの最小精度が30%を下回らないことを確認するだけで十分です。敵にとっては非常に頻繁に低くなります( 敵に対しては、算術平均さらに歪んだもの )。
3つの数値の幾何平均は、ほぼ同じ結果になりますが、大きな広がりがあります。

ここで、10%は1.95%、75%は93.98%になります。
多くの場合、一部のスキルを強化または弱体化するために、2つの乱数のいずれかが最大または最小に選択されると、より単純な操作が導入されます。
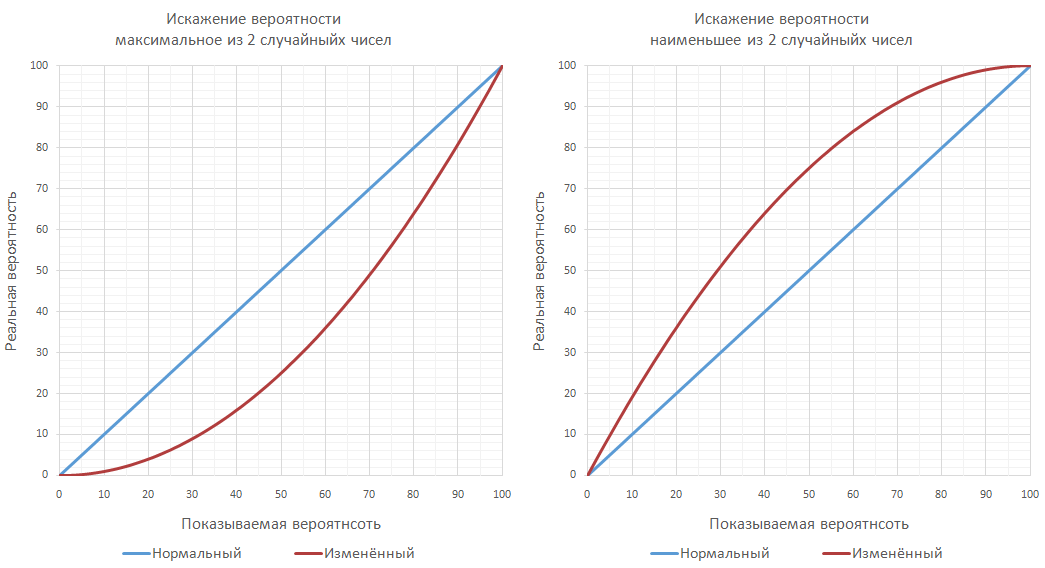
この結果、打撃の確率は大きく異なります。 たとえば、最小の数値を選択すると、10%の精度が19.02%に変換され、75%の精度が93.75%に変換されます。
このような方法は、例えば、スキル「Slippery Mind」のゲーム「Neverwinter Nights」で使用され、救いのチェックに失敗した場合、意志力の2回目のチェックが実行されます[ 3 ]。
ネバーウィンターナイツ-ピクシーウォリアー[ 4 ]
以下は、さまざまな計算方法の精度の歪みの表です。 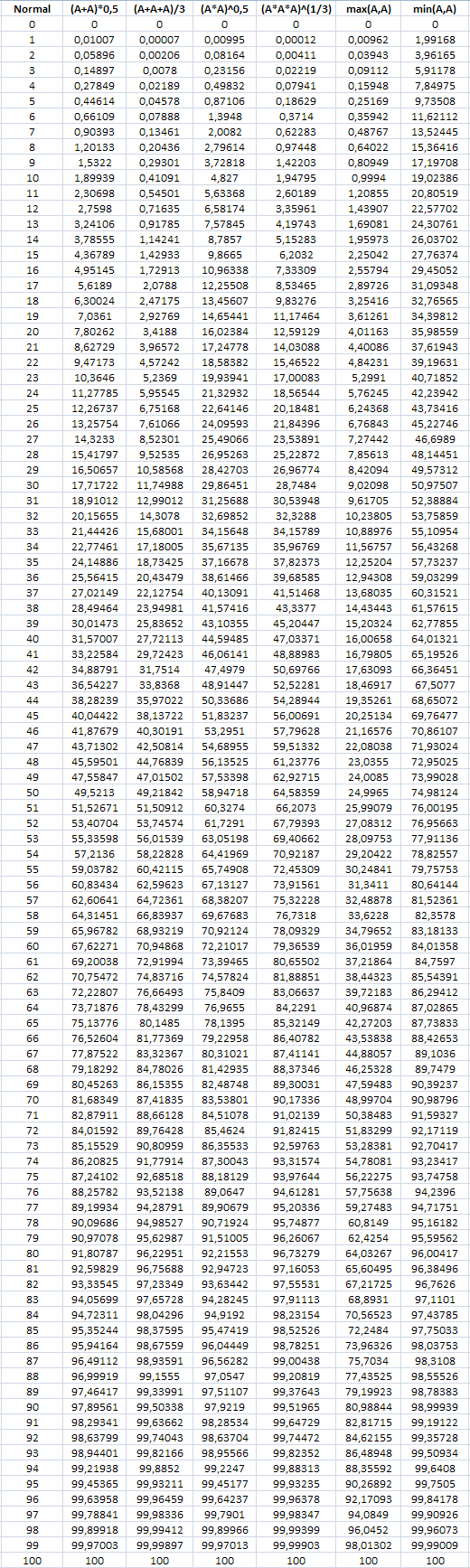

確率操作に関する以前の記事では、非常にまれなイベントのメソッドが示されました。イベントの確率は時間とともに増加しました。
開発者のCarsten Germerは、イベントだけでなく、まれなイベントにも制御されたランダム性の機能を使用しています[ 5 ]。 たとえば、10,000回に1回の確率で特にまれなボーナスの定期的な損失を保証するために、「ミス」が発生するたびに、次の順序でチャンスが増加します。 1から9800; 1〜9700 ...など、イベントが記録されるまで続きます。 また、頻繁な希少性の欠如を保証するために、最後の操作後の次の10回のチェック中に操作を100%ブロックする追加の変数を導入しました。リスク評価におけるプレイヤーの誤解[ 1 ]
この方法を使用すると、このまれなイベントの確率がどのように変化するかを次に示します。
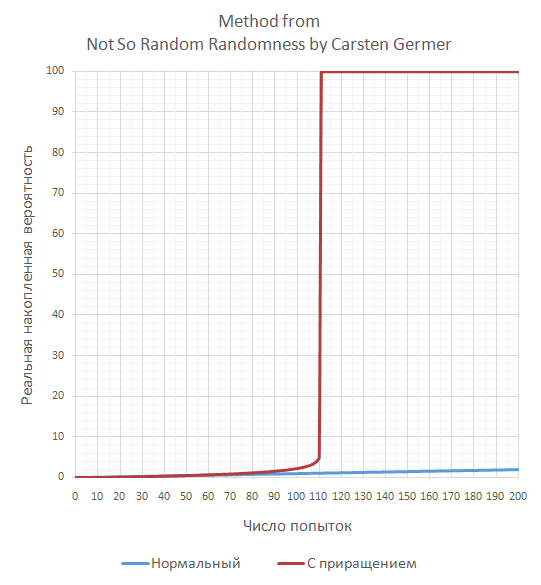
ご覧のとおり、最終的には10,000分の1の確率とは関係ありませんが、ゲームプレイの目的ではこれで十分である可能性があります。 開発者自身による実際の確率の意図しない隠蔽のように見えますが、これはプログラムの将来の改善において誤った決定につながる可能性があります。
以下では、試行回数が増加するにつれて少なくとも1回発生するという1%イベントの変更も示します。 歪みアルゴリズム:最初の10回の試行-保証されたミス。 次に、ミスが発生するたびに、ヒットする前に確率が1%(0.1%および0.01%)増加します。 その後、最初からすべて。
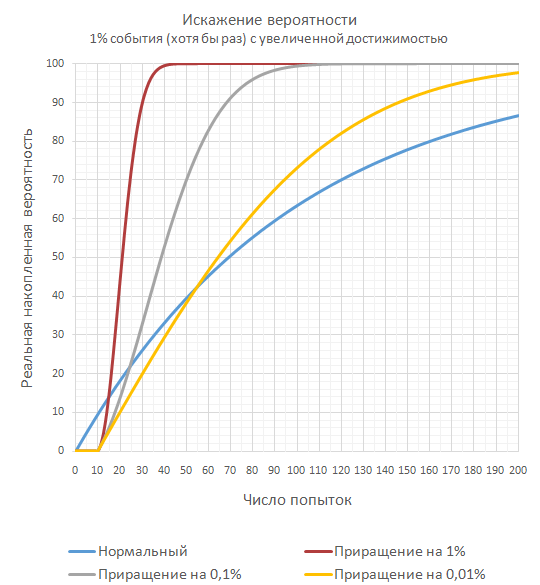
ただし、開発者としての主な目標が、1%のイベントのユーザーが連続して1000回のミスに陥らないようにすることである場合、200回連続してミスした後、100%のヒットを設定する方が簡単で透過的です。 これにより、プレイヤーのまれな困惑からあなたを救うことができ、将来の改善のためにプログラムコードをより簡潔で友好的にすることができます。
精度ボーナスを獲得するさまざまな方法
ゲームの精度に対するボーナスがほとんどなく、それらが開発者によって簡単に制御される場合、最も簡単な方法は、ベース値に単純に加算することで精度を直線的に増加させる最も単純なアプローチを使用することです 。 この方法は、ゲームに実装するのが最も簡単であり、プレイヤーは常に理解できます。 このアプローチでは、100%の精度を達成することができますが、これは常に開発者の計画に対応するとは限りません。
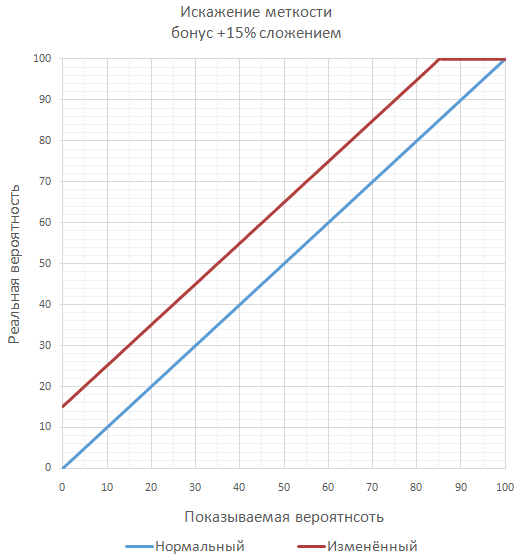
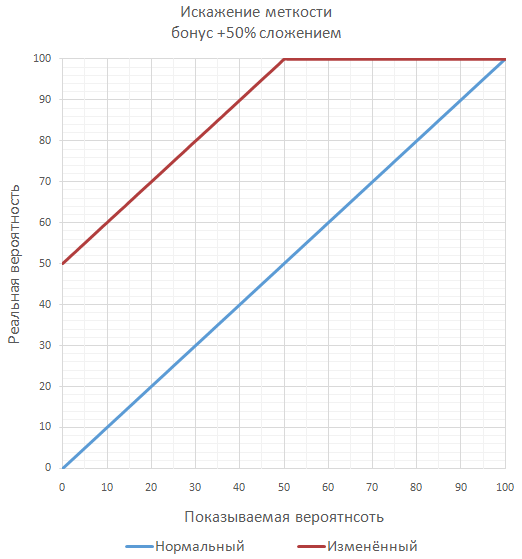
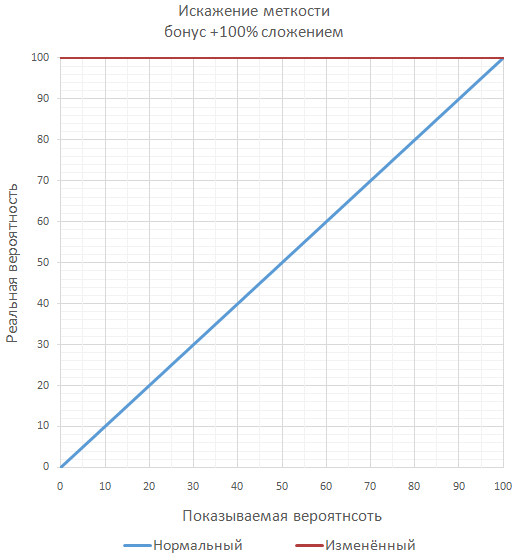
ゲームが精度に対して多くの重要なボーナスを計画している場合、保証された100%の精度を超えないように、一連の追加のスローとして最終精度を計算することができます( ほとんどの場合、別々ではありません )。 たとえば、精度が70%、ボーナスが50%の場合、ヒットの最終確率は85%になります。これは、少なくとも1回のヒットで十分なときに2回連続してスローをチェックするようになります。
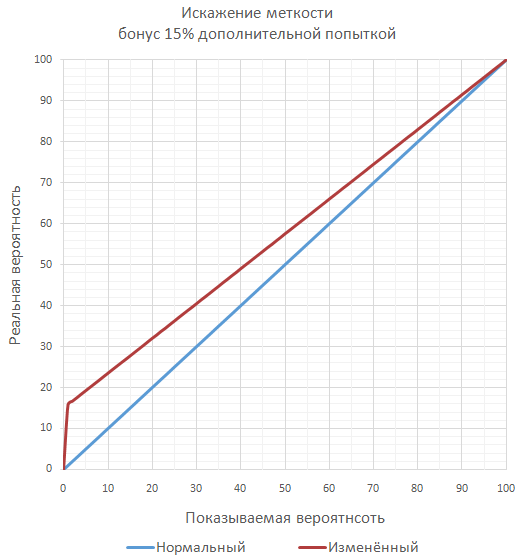
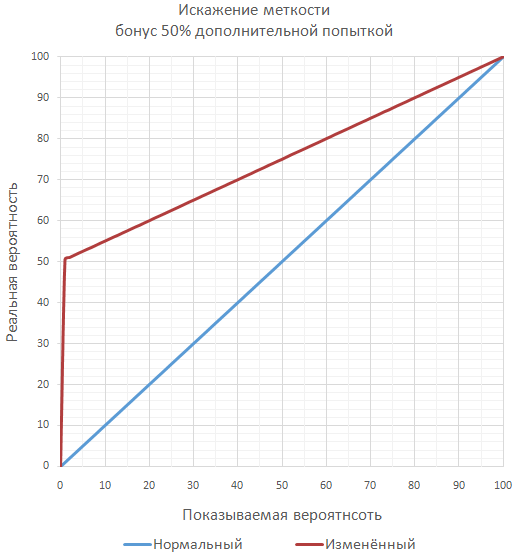
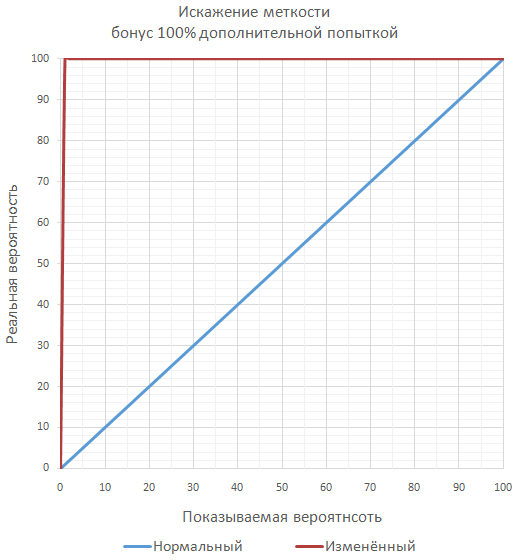
ちょっと変わったのは、ミスの確率を減らすというボーナスによって、ボーナスの本質を正確に変えるアプローチです。
// newAccuracy - % // baseAccuracy - % // bonusAccuracy - % let newAccuracy = 100 - ( (1 - baseAccuracy * 0.01) / (1 + bonusAccuracy * 0.01) ) * 100;
任意のボーナスで常にミスの可能性があることを保証します。 これにより、ゲームは100%以上、少なくとも1000%の「精度」にボーナスを与えることができます。 そして、まだミスの可能性があります。 しかし、プレイヤーは混乱する可能性が高いため、失望する可能性があります。
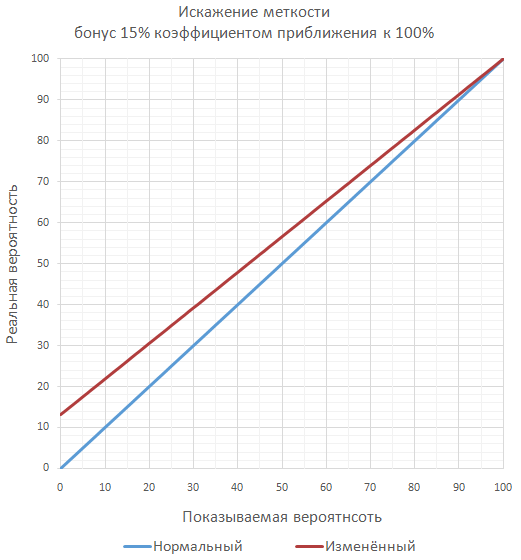
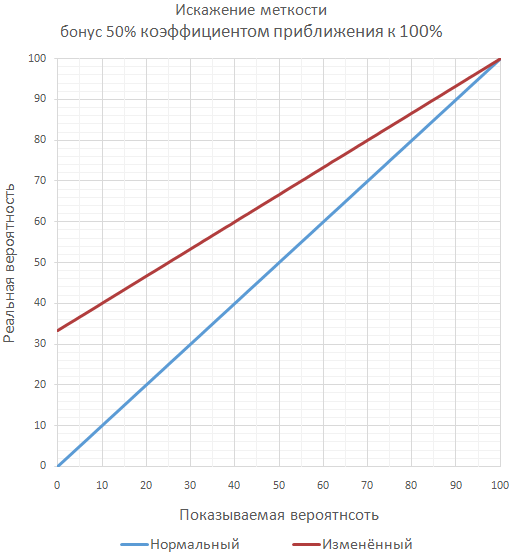
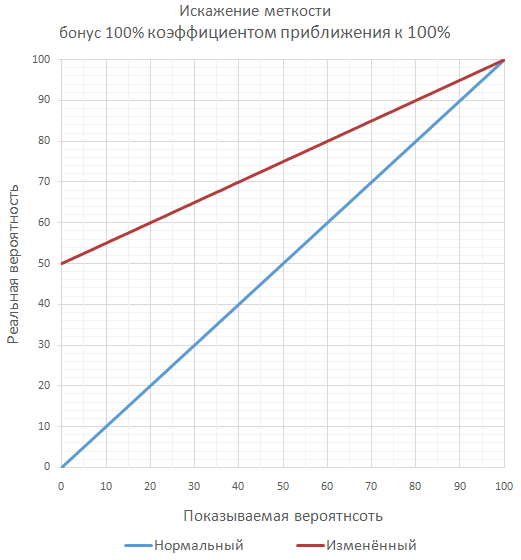
ほとんどの場合、プレーヤーにとって最も理解しやすく、開発者が実装しやすいように、ボーナスの単純な合計によるアプローチが使用されます。
サイコロベースのダメージ分布
このアイテムは、出版物「 Probability and Games:Damage Rolls from Red Blob Games [6] 」の視覚データに完全に基づいています。 ここでは、この出版物のいくつかの例と結論を簡単に紹介します。 元の記事では、より詳細な結論と対話型の分布図、およびさまざまな固有の組み合わせを選択するための対話型のカスタマイズ可能な関数を受け取ります。
異なるサイコロのダメージ計算の最も明白な(しかし唯一の)例は、最大値12でのダメージの計算に基づいて提示されます。結果は異なるサイコロを使用して取得できます( たとえば、ボードゲームをプレイして特別なサイコロがない場合) ):
1d12-12個の面を持つ1つのサイコロ

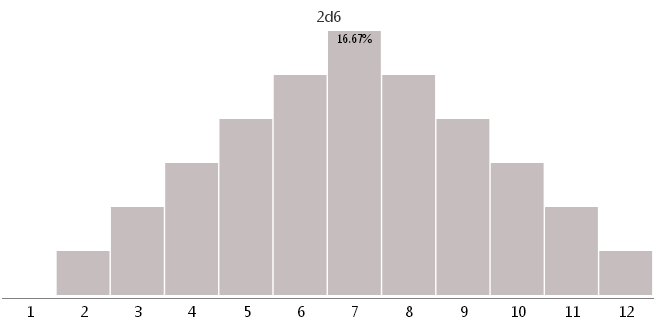
2d6-6つの異なる顔を持つ2つのサイコロ
3d4-4つの異なる顔を持つ3つのサイコロ
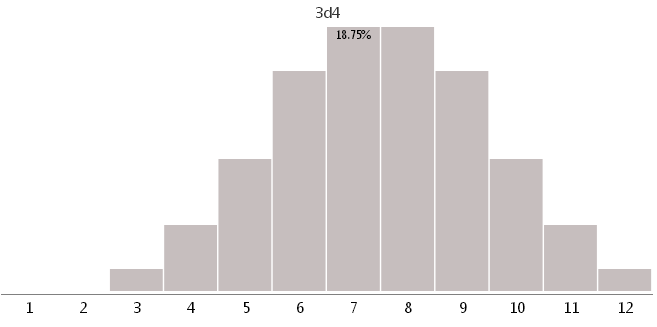
4d3-3つの異なる顔を持つ4つのサイコロ
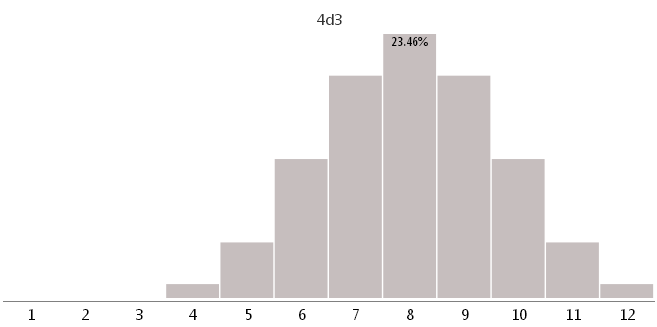
6d2-2つの異なる顔を持つ6つのサイコロ
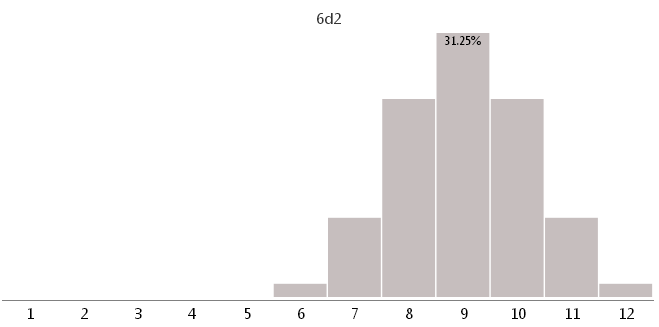
ご覧のとおり、不適切なキューブを使用すると、ゲームのバランスが大きく変わる可能性があります。
おわりに
したがって、次のトピックが検討されました。
- さまざまなチェック方法を使用した正確な操作。
- 精度ボーナスを獲得するさまざまな方法。
- 異なるサイコロベースのダメージ分布。
各メソッドは、開発者にとって有用な場合があります。 よりカジュアルな観客がいるゲームの場合、プレイヤーの成功確率が過大評価されるスペアリングアルゴリズムがより頻繁に選択され、興奮を高めるために、ありそうもない勝利の幻想が作成されます(以前の記事の1つで:[ 7 ])。
参照資料
1. リスク評価におけるプレイヤーの誤解。 開発中の乱数ジェネレーターの制御 。
2. ファイアーエムブレムWiki-乱数ジェネレーター 。
3. ネバーウィンターナイト2-クラスアビリティ-スリッパリーマインド 。
4. ネバーウィンターナイト-ピクシーウォリアー 。
5. ゲームデザインとプログラミングの「ランダムではないランダム」 。
6. 確率とゲーム:レッドブロブゲームのダメージロール 。
7. ゲームでのクローズコールの生成:「敗北寸前」または「ほぼ勝ちました 。 」