みなさんこんにちは!
ご想像のとおり、ニューラルネットワークと機械学習についてお話しましょう。 名前から、Mixture Density Networks、そしてMDNについて何が語られるかは明らかです。名前を翻訳してそのままにしておきたいとは思いません。 はい、はい、はい...少し退屈な数学と確率理論がありますが、残念ながら、または幸いなことに、機械学習の世界を想像するのが難しいかどうかを決めるのはあなた次第です。 しかし、私はあなたを安心させるために急いで、それは比較的小さく、それは非常に難しくありません。 とにかく、それをスキップできますが、PythonとPyTorchの少量のコードを見てください。そうです、PyTorchを使用してネットワークを作成し、結果のさまざまなグラフを作成します。 しかし、最も重要なことは、少し理解し、MDネットワークとは何かを理解する機会があるということです。
さあ、始めましょう!
回帰
最初に、知識を少し更新して、 線形回帰とは簡単に思い出してください。
ベクターがあります 値を予測する必要があります 、何らかの形で依存します 線形モデルを使用する:
エラー関数として、二乗誤差を使用します。
この問題は、SEの導関数を取得し、その値をゼロに設定することで直接解決できます。
したがって、単純に最小値を見つけます。SEは2次関数です。つまり、最小値は常に存在します。 その後、あなたはすでに簡単に見つけることができます :
それですべて、問題は解決しました。 ここで、線形回帰とは何かを思い出します。
もちろん、データ生成の性質に固有の依存関係は異なる可能性があり、その場合、モデルにある程度の非線形性を追加する必要があります。 マトリックスが存在するため、大規模で実際のデータの回帰問題を直接解決することも悪い考えです 寸法 、その逆行列を見つける必要があり、そのような行列が存在しないことがよくあります。 この場合、勾配降下に基づくさまざまな方法が役立ちます。 モデルの非線形性は、ニューラルネットワークの使用など、さまざまな方法で実装できます。
しかし、今はこれについてではなく、エラー関数について話しましょう。 データに非線形の関係がある場合、SEと対数尤度の違いは何ですか?
私たちは動物園、すなわちOLS、LS、SE、MSE、RSSを扱っています
これは本質的にまったく同じで、RSS-残差平方和、OLS-通常の最小二乗、LS-最小二乗、MSE-平均二乗誤差、SE-二乗誤差です。 さまざまなソースで、さまざまな名前を見つけることができます。 これの本質はたった一つ、 二次偏差です。 もちろん混乱する可能性がありますが、すぐに慣れることができます。
MSEは標準偏差であり、トレーニングデータセット全体の誤差の特定の平均値であることに注意してください。 実際には、MSEが通常使用されます。 式は特に変わりません:
-データセットのサイズ、 -モデルの予測 。
MSEは標準偏差であり、トレーニングデータセット全体の誤差の特定の平均値であることに注意してください。 実際には、MSEが通常使用されます。 式は特に変わりません:
-データセットのサイズ、 -モデルの予測 。
やめて! 可能性は? これは確率論からのものです。 そうです-これは純粋な確率論です。 しかし、二次偏差はどのように尤度関数に関連するのでしょうか? そしてそれがどうなるか。 これは、最尤(Maximum Likelihood)を見つけること、およびより正確に言えば、その平均で正規分布に関連しています。 。
これがそうであることを理解するために、二乗偏差関数をもう一度見てみましょう。
ここで、尤度関数が正規形、つまりガウス分布または正規分布を持っていると仮定します。
一般に、尤度関数とは何であるかは説明しませんが、他の場所で読むことができます。条件付き確率の概念、ベイズの定理などについても理解しておく必要があります。 これはすべて、学校と大学の両方で研究されている純粋な確率論に当てはまります。
さて、正規分布式を思い出して、次のようになります
標準偏差を入れた場合 関数の最小値を見つけることはそれらに依存しないため、式(2)のすべての定数を削除します。 次に、これが表示されます。
まだ何も好きですか いや? さて、関数の対数を取るとどうなりますか? 一般に、対数から1つのプラスがあります。乗算は合計に、度は乗算に、そして -この特性については、自然対数について話していること、そして厳密に言えば、 。 そして一般的に、関数の対数はその最大値を変更せず、これは私たちにとって最も重要な機能です。 Log-LikelihoodとLikelihoodとの関係、およびこれがなぜ役立つのかについては、後ほど簡単に説明します。 そして、私たちがしたこと:すべての定数を削除し、尤度関数の対数を取りました。 また、マイナス記号も削除したため、対数尤度が負の対数尤度(NLL)に変わり、それらの間の接続もボーナスとして説明されます。 その結果、NLL関数が得られました。
RSS関数をもう一度見てください(1)。 はい、彼らは同じです! まさに! それも見られます 。
MSE標準偏差関数を使用する場合、次のようになります。
どこで -数学的な期待 -モデルパラメータ。将来的には次のように指定します。 。
結論:回帰問題の誤差関数としてLSファミリーを使用する場合、分布がガウス分布の場合の最尤関数を見つける問題を本質的に解決します。 そして予測値 正規分布の平均に等しい。 そして今、私たちはこれらすべてがどのように関係しているか、確率論がどのように関係しているのか(尤度関数と正規分布とともに)、標準偏差法またはOLSを知っています。 詳細については、[2]をご覧ください。
そして、ここに約束されたボーナスがあります。 さまざまなエラー関数間の関係について話しているので、考慮する必要があります(必ずしも読む必要はありません)。
クロスエントロピー、尤度、対数尤度および負の対数尤度の関係
データがあるとします 、各ポイントは特定のクラスに属します。たとえば 。 合計 クラス、クラス1が発生する 回、クラス2- 時間とクラス - 回。 このデータで、いくつかのモデルを訓練しました 。 尤度関数(尤度)は次のようになります。
どこで -クラスの予測確率 。
尤度関数の対数を取り、対数尤度を取得します。
確率 確率の定義に基づいて、0から1の範囲にあります。 したがって、対数は負の値になります。 Log-Likelihoodに-1を掛けると、関数Negative Log-Likelihood(NLL)が得られます。
NLLを点の数で割ると 、 次に取得します:
クラスの実際の確率は 等しい: 。 ここから次のものが得られます。
クロスエントロピーの定義を見れば 次に取得します:
クラスが2つしかない場合 (バイナリ分類)バイナリクロスエントロピーの式を取得します(よく知られている名前Log-Lossを満たすこともできます)。
このすべてから、場合によっては、クロスエントロピーを最小化することは、NLLを最小化すること、または尤度関数(尤度)または対数尤度の最大値を見つけることと同等であることが理解できます。
例。 バイナリ分類を検討してください。 クラス値があります:
本当の確率 クラス0は等しい 、クラス1は等しい 。 クラス0の確率を予測するバイナリ分類器があるとします クラス1のそれぞれの例では、確率は 。 さまざまな予測の対数損失関数の値をプロットしてみましょう :
。 クラス0の確率を予測するバイナリ分類器があるとします クラス1のそれぞれの例では、確率は 。 さまざまな予測の対数損失関数の値をプロットしてみましょう :
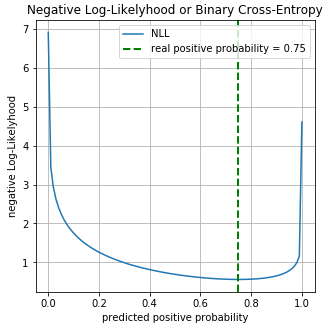
グラフでは、対数損失関数の最小値がポイント0.75に対応していることがわかります。 モデルがソースデータの分布を完全に「学習」した場合、 。
どこで -クラスの予測確率 。
尤度関数の対数を取り、対数尤度を取得します。
確率 確率の定義に基づいて、0から1の範囲にあります。 したがって、対数は負の値になります。 Log-Likelihoodに-1を掛けると、関数Negative Log-Likelihood(NLL)が得られます。
NLLを点の数で割ると 、 次に取得します:
クラスの実際の確率は 等しい: 。 ここから次のものが得られます。
クロスエントロピーの定義を見れば 次に取得します:
クラスが2つしかない場合 (バイナリ分類)バイナリクロスエントロピーの式を取得します(よく知られている名前Log-Lossを満たすこともできます)。
このすべてから、場合によっては、クロスエントロピーを最小化することは、NLLを最小化すること、または尤度関数(尤度)または対数尤度の最大値を見つけることと同等であることが理解できます。
例。 バイナリ分類を検討してください。 クラス値があります:
y = np.array([0, 1, 1, 1, 1, 0, 1, 1]).astype(np.float32)
本当の確率 クラス0は等しい 、クラス1は等しい

グラフでは、対数損失関数の最小値がポイント0.75に対応していることがわかります。 モデルがソースデータの分布を完全に「学習」した場合、 。
ニューラルネットワーク回帰
それで、私たちはもっと面白い練習に来ました。 ニューラルネットワーク(ニューラルネットワーク)を使用して回帰の問題を解決する方法を見てみましょう。 Pythonプログラミング言語ですべてを実装し、PyTorch深層学習ライブラリを使用してネットワークを作成します。
ソースデータの生成
入力データ 一様分布を使用して生成し、-15〜15の間隔を取ります 。 ポイント 方程式を使用して取得します。
どこで 次元のノイズベクトルです パラメーター付き正規分布を使用して取得: 。
データ生成
N = 3000 # IN_DIM = 1 OUT_DIM = IN_DIM x = np.random.uniform(-15., 15., (IN_DIM, N)).T.astype(np.float32) noise = np.random.normal(size=(N, 1)).astype(np.float32) y = 0.5*x+ 8.*np.sin(0.3*x) + noise # 3 x_train, x_test, y_train, y_test = train_test_split(x, y) #

受信したデータのグラフ。
ネットワーク構築
通常のフィードフォワードニューラルネットワークまたはFFNNを作成します。
FFNNの構築
class Net(nn.Module): def __init__(self, input_dim=IN_DIM, out_dim=OUT_DIM, layer_size=40): super(Net, self).__init__() self.fc = nn.Linear(input_dim, layer_size) self.logit = nn.Linear(layer_size, out_dim) def forward(self, x): x = F.tanh(self.fc(x)) # 4 x = self.logit(x) return x
私たちのネットワークは、40個のニューロンの次元と活性化機能を備えた1つの隠れ層で構成されています-双曲線正接:
出力レイヤーは、アクティベーション関数のない通常の線形変換です。
学習と結果の取得
オプティマイザーとして、AdamOptimizerを使用します。 学習のエポック数= 2000、学習率(学習率またはlr)= 0.1。
FFNNトレーニング
def train(net, x_train, y_train, x_test, y_test, epoches=2000, lr=0.1): criterion = nn.MSELoss() optimizer = optim.Adam(net.parameters(), lr=lr) N_EPOCHES = epoches BS = 1500 n_batches = int(np.ceil(x_train.shape[0] / BS)) train_losses = [] test_losses = [] for i in range(N_EPOCHES): for bi in range(n_batches): x_batch, y_batch = fetch_batch(x_train, y_train, bi, BS) x_train_var = Variable(torch.from_numpy(x_batch)) y_train_var = Variable(torch.from_numpy(y_batch)) optimizer.zero_grad() outputs = net(x_train_var) loss = criterion(outputs, y_train_var) loss.backward() optimizer.step() with torch.no_grad(): x_test_var = Variable(torch.from_numpy(x_test)) y_test_var = Variable(torch.from_numpy(y_test)) outputs = net(x_test_var) test_loss = criterion(outputs, y_test_var) test_losses.append(test_loss.item()) train_losses.append(loss.item()) if i%100 == 0: sys.stdout.write('\r Iter: %d, test loss: %.5f, train loss: %.5f' %(i, test_loss.item(), loss.item())) sys.stdout.flush() return train_losses, test_losses net = Net() train_losses, test_losses = train(net, x_train, y_train, x_test, y_test)
それでは、学習成果を見てみましょう。
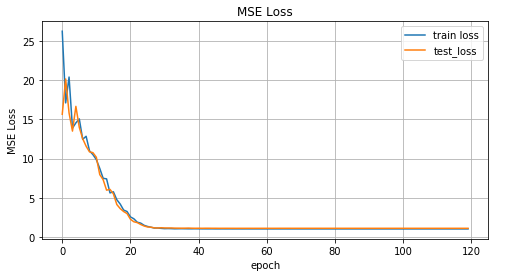
トレーニングの反復に応じたMSE関数値のグラフ、トレーニングデータとテストデータの値のグラフ。
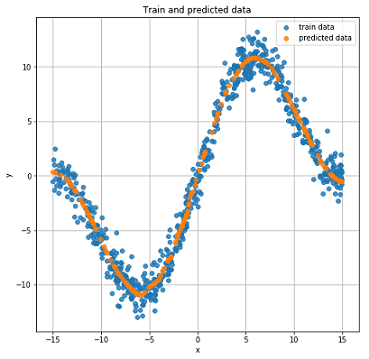
テストデータに関する実際の予測結果。
反転データ
タスクを複雑にし、データを反転させます。
データ反転
x_train_inv = y_train y_train_inv = x_train x_test_inv = y_train y_test_inv = x_train

反転データグラフ。
予測用 前のセクションの直接配信ネットワークを使用して、これをどのように処理するかを見てみましょう。
inv_train_losses, inv_test_losses = train(net, x_train_inv, y_train_inv, x_test_inv, y_test_inv)
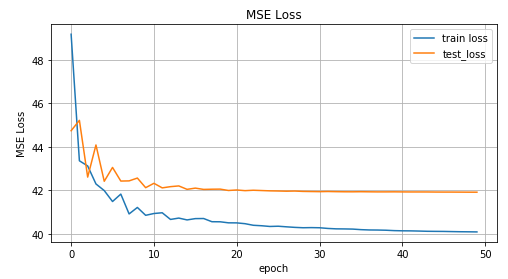
トレーニングの反復に応じたMSE関数値のグラフ、トレーニングデータとテストデータの値のグラフ。
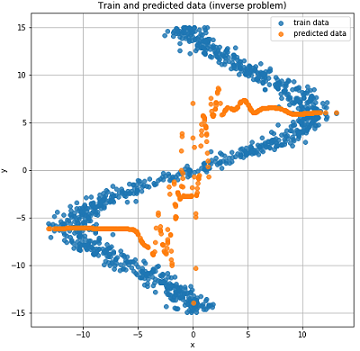
テストデータに関する実際の予測結果。
上のグラフからわかるように、私たちのネットワークはそのようなデータにまったく対応しておらず、単に予測することはできません。 そして、このすべてが起こりました 複数のポイントに対応する場合があります 。 ノイズについてはどうですか? 彼はまた、 いくつかの値を取得できます 。 はい、そうです。 しかし、全体のポイントは、ノイズにもかかわらず、それはすべて1つの明確な分布であったということです。 そして、我々のモデルは本質的に予測したので 、MSEの場合は正規分布の平均値(記事の最初の部分で説明されている理由)であり、「直接」タスクにうまく対処しました。 それ以外の場合は、1つの異なる分布を取得します したがって、正規分布が1つだけでは良い結果を得ることができません。
混合密度ネットワーク
楽しみが始まります! 混合密度ネットワーク(以下、MDNまたはMDネットワーク)とは何ですか? 一般に、これは複数の分布を一度にシミュレートできる特定のモデルです。
なんて奇妙な式だとあなたは言います。 それを理解しましょう。 私たちのMDネットワークは、平均 および分散 複数のディストリビューション用。 式(5)で -各ポイントの個別の分布のいわゆる有意因子 、特定の混合係数、または各分布が特定のポイントにどの程度寄与するか。 合計 分布。
についてもう少し言います -実際には、これも分布であり、ポイントの確率を表します 条件になります 。
ふふ、再び、この数学、すでに何かを書きましょう。 それで、ネットワークの実装を始めましょう。 私たちのネットワークのために 。
self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance
ネットワークの出力レイヤーを定義します。
x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x)
エラー関数または損失関数、式(5)を記述します。
def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses))
完全なMDNビルドコード
COEFS = 30 class MDN(nn.Module): def __init__(self, input_dim=IN_DIM, out_dim=OUT_DIM, layer_size=50, coefs=COEFS): super(MDN, self).__init__() self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance self.out_dim = out_dim self.coefs = coefs def forward(self, x): x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x) return pi, mu, sigma_sq # def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) # def loss_fn(y, pi, mu, sigma_sq): losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses)) return loss
MDネットワークはすぐに使用できます。 ほぼ準備完了。 彼女を訓練し、結果を見ることが残っています。
MDNトレーニング
def train_mdn(net, x_train, y_train, x_test, y_test, epoches=1000): optimizer = optim.Adam(net.parameters(), lr=0.01) N_EPOCHES = epoches BS = 1500 n_batches = int(np.ceil(x_train.shape[0] / BS)) train_losses = [] test_losses = [] for i in range(N_EPOCHES): for bi in range(n_batches): x_batch, y_batch = fetch_batch(x_train, y_train, bi, BS) x_train_var = Variable(torch.from_numpy(x_batch)) y_train_var = Variable(torch.from_numpy(y_batch)) optimizer.zero_grad() pi, mu, sigma_sq = net(x_train_var) loss = loss_fn(y_train_var, pi, mu, sigma_sq) loss.backward() optimizer.step() with torch.no_grad(): if i%10 == 0: x_test_var = Variable(torch.from_numpy(x_test)) y_test_var = Variable(torch.from_numpy(y_test)) pi, mu, sigma_sq = net(x_test_var) test_loss = loss_fn(y_test_var, pi, mu, sigma_sq) train_losses.append(loss.item()) test_losses.append(test_loss.item()) sys.stdout.write('\r Iter: %d, test loss: %.5f, train loss: %.5f' %(i, test_loss.item(), loss.item())) sys.stdout.flush() return train_losses, test_losses mdn_net = MDN() mdn_train_losses, mdn_test_losses = train_mdn(mdn_net, x_train_inv, y_train_inv, x_test_inv, y_test_inv)
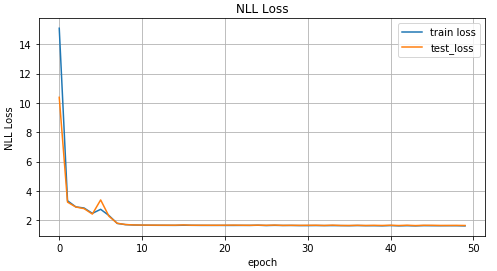
トレーニングの反復に依存する損失関数値のグラフ、トレーニングデータとテストデータの値のグラフ。
ネットワークはいくつかの分布の平均値を学習しているので、これを見てみましょう。
pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv)))
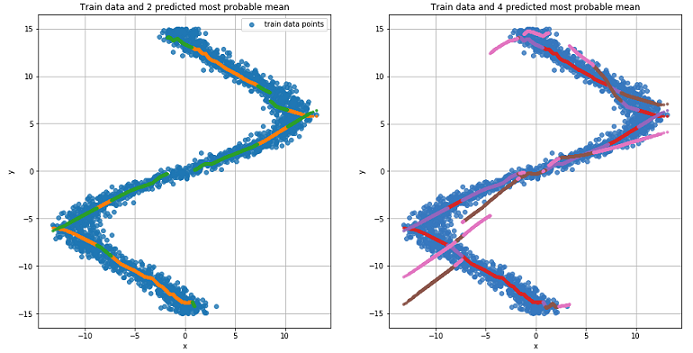
各ポイントの最も可能性の高い2つの平均値のグラフ(左)。 各ポイントの最も可能性の高い4つの平均値のグラフ(右)。
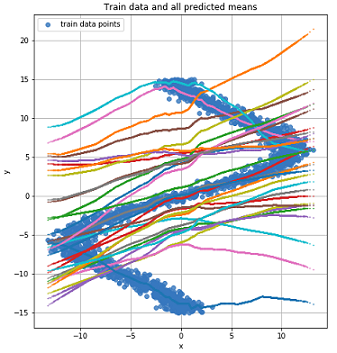
各ポイントのすべての平均値のグラフ。
データを予測するために、いくつかの値をランダムに選択します そして 値に基づいて 。 そして、それらに基づいて、ターゲットデータを生成します 正規分布を使用します。
結果の予測
def rand_n_sample_cumulative(pi, mu, sigmasq, samples=10): n = pi.shape[0] out = Variable(torch.zeros(n, samples, OUT_DIM)) for i in range(n): for j in range(samples): u = np.random.uniform() prob_sum = 0 for k in range(COEFS): prob_sum += pi.data[i, k] if u < prob_sum: for od in range(OUT_DIM): sample = np.random.normal(mu.data[i, k*OUT_DIM+od], np.sqrt(sigmasq.data[i, k])) out[i, j, od] = sample break return out pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv))) preds = rand_n_sample_cumulative(pi, mu, sigma_sq, samples=10)
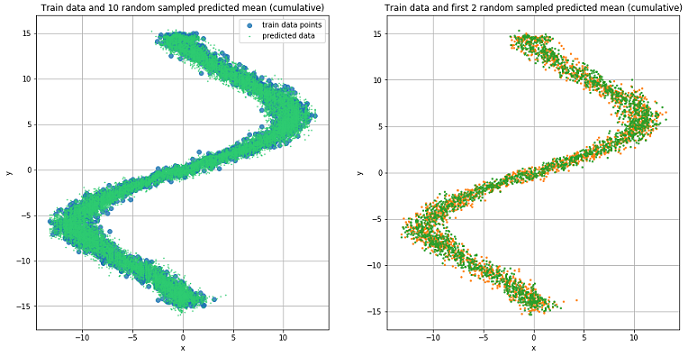
ランダムに選択された10個の値の予測データ そして (左)と2つ(右)。
図から、MDNは「逆」タスクで素晴らしい仕事をしたことがわかります。
より複雑なデータを使用する
MDネットワークがスパイラルデータなどのより複雑なデータをどのように処理するかを見てみましょう。 デカルト座標の双曲線スパイラルの方程式:
スパイラルデータ生成
N = 2000 x_train_compl = [] y_train_compl = [] x_test_compl = [] y_test_compl = [] noise_train = np.random.uniform(-1, 1, (N, IN_DIM)).astype(np.float32) noise_test = np.random.uniform(-1, 1, (N, IN_DIM)).astype(np.float32) for i, theta in enumerate(np.linspace(0, 5*np.pi, N).astype(np.float32)): # 6 r = ((theta)) x_train_compl.append(r*np.cos(theta) + noise_train[i]) y_train_compl.append(r*np.sin(theta)) x_test_compl.append(r*np.cos(theta) + noise_test[i]) y_test_compl.append(r*np.sin(theta)) x_train_compl = np.array(x_train_compl).reshape((-1, 1)) y_train_compl = np.array(y_train_compl).reshape((-1, 1)) x_test_compl = np.array(x_test_compl).reshape((-1, 1)) y_test_compl = np.array(y_test_compl).reshape((-1, 1))

スパイラルデータのグラフ。
楽しみのために、通常のフィードフォワードネットワークがこのようなタスクにどのように対処するかを見てみましょう。
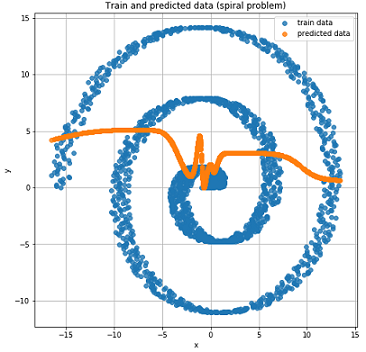
予想どおり、フィードフォワードネットワークでは、このようなデータの回帰問題を解決できません。
スパイラルデータのトレーニングには、前述および作成したMDネットワークを使用します。
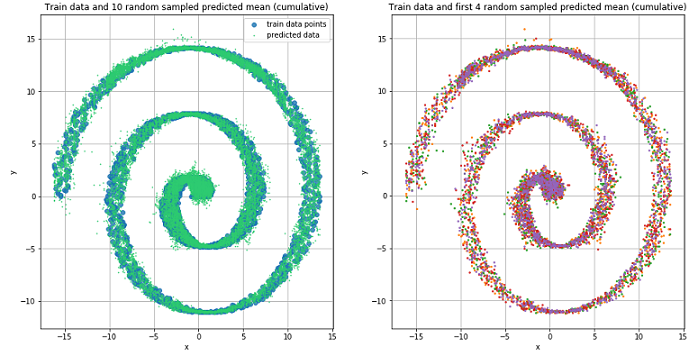
このような状況では、混合密度ネットワークがうまく対処しました。
おわりに
この記事の冒頭で、線形回帰の基本を思い出しました。 正規分布とMSEの平均を見つけることの間で共通していることがわかりました。 NLLとクロスエントロピーの接続方法を分解しました。 そして最も重要なことは、混合分布から取得したデータから学習できるMDNモデルを見つけたことです。 少し数学があったという事実にもかかわらず、この記事が明確で興味深いものになったことを願っています。
完全なコードはGitHubで表示できます。
文学
- 混合密度ネットワーク(Christopher M. Bishop、アストン大学、バーミンガム、コンピュータサイエンスおよび応用数学科、ニューラルコンピューティングリサーチグループ) -この記事では、MDネットワークの理論について詳しく説明しています。
- 最小二乗および最尤(MROsborne)