🔊 🧚🏼 🧖 企業の階層構造における従業員の負の選択 🎤 ⛈️ 🏂🏽

エントリー

私たちは皆、組織における採用がいかに重要かを知っています。しかし、多くの場合、組織の構造がこのスタッフの効率にどのように影響するかについて、かなりあいまいなアイデアを持っています。または、たとえば、人員配置表のさまざまなパラメータを持つ従業員の分布が作業効率にどのように影響するか。

この質問が提起されると、これらは通常、企業の繁栄よりもむしろ自分のプロモーションに興味がある水仙を推進し、やる気にさせる階層構造など、高品質の説明を含む退屈な教科書からのヒューリスティックな一般的な単語です。

この質問のいくつかの側面は数学的にモデル化するのが非常に簡単であり、これは企業を管理するための新しいオプションの機会を開く可能性があることがわかります。従業員の特性に関するかなり単純な仮定のコンテキストでは、組織の構造を設定するときだけで、非常に多くの重要で興味深い特性が単独でクロールします。そして、質問は次のように提起することができます-これを組織の利益のために使用する機会はありますか？

モデルの説明

ステップバイステップは、大規模な組織の発展をシミュレートします。

O

$O$ 、階層の各レベルの各作業者は、2つの変数と2つのサブセットで記述されます。

H_i = \ {C、D、E、W_i \}、

$H_i = \ {C、D、E、W_i \}、$

どこで

\ {... \}

$\ {... \}$ -多くの

C

$C$ -特定の人物のすべてのボスのセット、

D

$D$ -特定の個人のすべての部下のセット。

W_{i}

$W_i$ -個人がどのようにタスクを実行するかについての個人的な有効性（生産性）の程度

i

$i$ -レベル。すべてのレベルで

W_{i} = U （ 0, 1 ） + 0.5

$W_i = U（0,1）+ 0.5$ どこで

U （ 0, 1 ）

$U（0,1）$ -均一な分布。したがって、すべての平均的な個人の生産性は1です。ここで、ピーターの原則を思い出すのが適切です。この有効性のタスクの場合、「階層システムでは、各個人は自分の無能の低いレベルに上昇する傾向があります。」人がより効果的でないという事実ではありません。効率が落ちたところまでしか上昇しません。私たちが知っているように、最も効果的な集団農場の議長は、常に少なくとも許容できるミルクメイドではありません。ただし、後で説明するように、この原則は絶対理想主義的な状況についても説明しています（正当に批判されているため、なおさらです）。

E = U （ 0, 1 ）

$E = U（0,1）$ -人間のエゴイズムの度合い。ここで、エゴイズムとは、生産性や仕事関数のパフォーマンスに関係しないことを行う特定の「蒸留」能力のみを意味しますが、人の意見では、キャリアの向上に貢献する必要があります。

組織モデルが生成されます

N

$N$ 最初にランダムに分散される上記の特性を持つ人

L

$L$ レベル。各レベルの容量は、次の理由で設定されます。

私たちは皆、バーでビールを注文する数学者についてのジョークを知っています。

s u m_{i = 1}^{i n f t y} f r a c 1 2^{i} = 1

$\ sum_ {i = 1} ^ {\ infty} {\ frac {1} {2 ^ i}} = 1$

だから

i

$i$ レベルの場合、そのレベルの人数は次の式で計算できます。

N_i = \ lfloor \ frac {N} {S \ cdot 2 ^ i} + 0.5 \ rfloor、S = \ sum_ {i = 1} ^ {L} {\ frac {1} {2 ^ i}

$N_i = \ lfloor \ frac {N} {S \ cdot 2 ^ i} + 0.5 \ rfloor、S = \ sum_ {i = 1} ^ {L} {\ frac {1} {2 ^ i}$

どこで

l f l o o r x r f l o o r

$\ lfloor x \ rfloor$ -切り捨て（床）。

S

$S$ -正規化量、最終的に正確に判明するように

N

$N$ 人。

したがって、完全に組織化

O

$O$ 次元ベクトルとして定義

L

$L$ どこで

i

$i$ 多くの従業員が設定したレベル

O_i = \ {H_i ^ 1、H_i ^ 2、...、H_i ^ {N_i} \}。

$O_i = \ {H_i ^ 1、H_i ^ 2、...、H_i ^ {N_i} \}。$

各人には、ボスのセット（上位レベルを除く）と部下のセット（下位レベルを除く）があります-

C 、 D

$C、D$ 。各ユーザーにこのリストを設定するには、次のアルゴリズムを使用します。

組織を与えてみましょう

O

$O$ 。それからすべての人のために

H i n O

$H \ in O$ 所有している

O_{i}

$O_i$ リスト

D

$D$ から

K

$K$ 部下は次のように設定されます。

HD=[] if Hi != 0: HD = random.shuffle(O[i-1])[:K] for dependant in HD: dependant.C.append(H)

2つの頂点間に複数のパスが存在する可能性があるため、ツリーの精神では階層の最上部からグラフが拡大しますが、ツリーは拡大しません。

各反復で、各人のパフォーマンス

H_{i}

$H_i$ 次の式に従って計算されます。

P_{H_{i}} = （ 1 - E^{K} ） c d o t W_{i} c d o t m i n （ 1 c u p P_{D} ） 、

$P_ {H_i} =（1-E ^ K）\ cdot W_i \ cdot min（1 \ cup P_D）、$

どこで

P_D = \ {P_ {D_0}、P_ {D_1}、... \}

$P_D = \ {P_ {D_0}、P_ {D_1}、... \}$ -すべての部下の多くの生産性。この式の本質は、個々の部下のエゴイズムがその数によって平準化されることです

K

$K$ 、わがままを考慮しないシステム全体のパフォーマンスは、従属の最も弱いリンクのパフォーマンスです

分 （ 1 \カ ッ プ P_{D} ）

$分（1 \カップP_D）$ 。

次に、各反復で、すべての人々のパフォーマンスが考慮されます。

P = s u m_{i = 0}^{N} P_{i}

$P = \ sum_ {i = 0} ^ {N} {P_i}$

構造の有効性の主な尺度として、人数に正規化された生産性が使用されます。

P^{'} = P / N

$P '= P / N$ 。この指標は、得られた結果が、だれも利己的で誰の生産性も1でなかった場合にどの程度の結果が得られたかを示します

各反復の終わりに、フレームの進行段階が行われます。毎ターン

R

$R$ ランダムな人々が退職（退職または他の何か）した後、彼らの直接部下が空席を奪い合い、ピラミッドの最下部が追加されます

R

$R$ 階層を下位レベルに下げて却下しました。これは、新しいエンティティを導入せず、結果の追加のランダムウォークを回避するために行われます。

競合の3つの修正が検討されました。

昇進が従業員の利己心のみに依存する、利己的な昇進のシナリオ、
理想的な昇進のシナリオ。昇進のレベルでの昇進が従業員の生産性のみに依存する場合、
混合プロモーションシナリオ、以下で説明するより複雑なプロモーションモデル。

利己的なプロモーションのシナリオ

競争は、解雇された人の各部下が昇進のための闘争に参加する機会をある程度持っていることです。勝者は、次の式に従って考慮されます。

勝 者 = 最 大 （ E_{D_{H}} * R n d （ K ） ） 、

$勝者=最大（E_ {D_H} * Rnd（K））、$

どこで

E_{D_{H}}

$E_ {D_H}$ -部下間のすべてのエゴイズムのベクトル

D_{H}

$D_H$ 元上司

H

$H$ 、*-要素ごとの乗算、

R n d （ K ）

$Rnd（K）$ からのランダム値のベクトルです

U （ 0, 1 ）

$U（0,1）$ 寸法

K

$K$ 。

理想的なシナリオ

勝者は、次の式に従って考慮されます。

勝 者 = 最 大 （ W_{D_{H} 、 i} * R n d （ K ） ） 、

$勝者=最大（W_ {D_H、i} * Rnd（K））、$

どこで

W_{D_{H} 、 i}

$W_ {D_H、i}$ -部下間の潜在的なすべての生産性のベクトル

D_{H}

$D_H$ のために

i

$i$ 元上司

H

$H$ 。

混合プロモーションのシナリオ

先進国の1つで採用されている競争モデルを採用することが提案されました。 「ピラミッドは2つの半分に分かれています。 ボトムラインはパフォーマンスとの相関関係です。 上記から、昇進は、利己主義とチェーンダウン全体の総生産性の積によって決定されます。 下半分から上半分への移行は純粋なエゴイズムです。」

次のように実装できます。

 prob = [] center = round(L/2) for D in HD: if Di<center: prob.append(DE + DW) elif Di == center: prob.append(DE) else: prob.append(DE*(D.P+Col(D))) s = sum(prob) r = random.random() for p in prob: r = r - p/s if r<0: winner = HD[i]

Col（D）関数は、すべての部下のパフォーマンスを要約する再帰関数です。

 def Col(H): result = 0 for D in HD: result += DP + Col(D)    return result

シミュレーション中はどうなりますか？

利己的なプロモーションのシナリオ

利己的な昇進のシナリオによる計算の結果を考えてみましょう。この場合、10,000人の人口に対して60回の反復が「存続」します。最初のグラフは、長年にわたるパフォーマンスの変化です。すべての従業員がすべてのレベルで完全な効率を達成した場合にのみ、値1になることに注意してください。 2つ目は、エゴイストの分布が年月とともにどのように変化するかです（最初はすべてのエゴイストがレベルの全人口の20％のレベルにあり、かなり楽観的であることがわかります）。

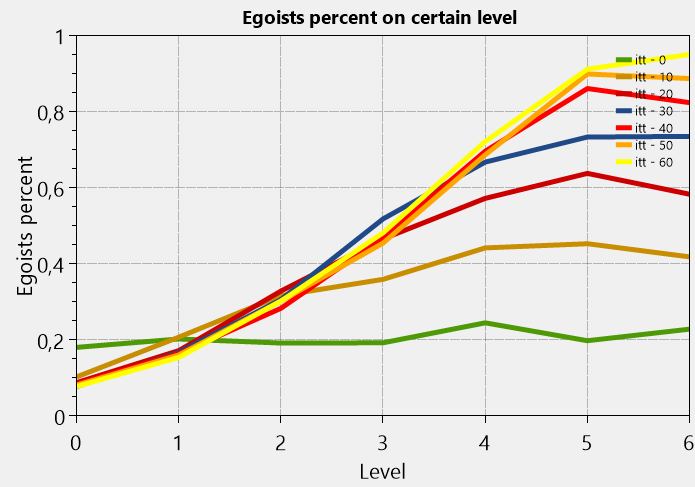
生産性が2倍以上低下します。上位レベルのエゴイストの数は増加しており、指数関数的に上位レベルを完全に埋めようとしています。

まあ、明らかな結論は、エゴイズムは常に良いパフォーマンスと組み合わされているわけではないため、上位レベルのエゴイストの数が増え、生産性が低下しているということです。誰が疑うでしょう。

理想的なシナリオ

すべて同じパラメーター。 10,000人、60回の反復、最初のどのレベルでもエゴイストの20％。コードは1行変更されました。場所の競争の基準。エゴイズムの代わりに、潜在的な生産性のレベルは、今では追放されたボスのレベルにあります。特定のケースでは、このようになります。

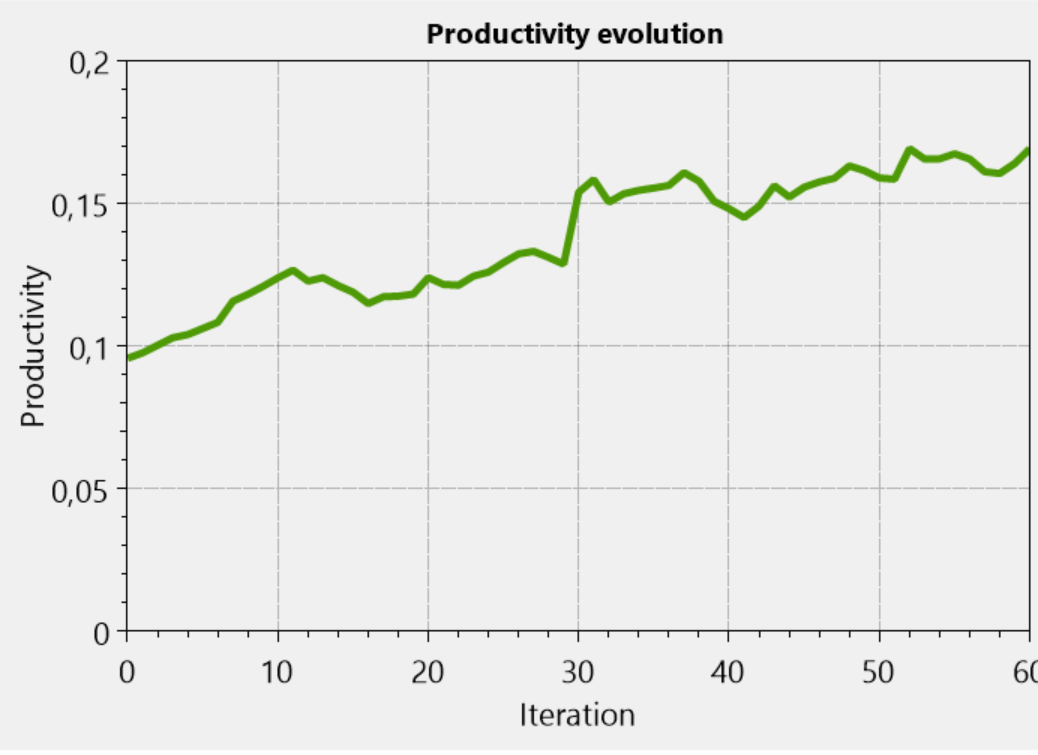
エゴイズムのレベルは生産性のレベルとはまったく関係がないため、生産的な人々をより高いレベルに再配分しても、このレベルのエゴイズムには影響しません。しかし同時に、優秀な人材の昇進により、すべての生産性が向上しています。

混合プロモーションのシナリオ

パラメーターは同じです。ちょうど別のルール。階層のさまざまなレベルの評価を分離するための複雑なスキーム。

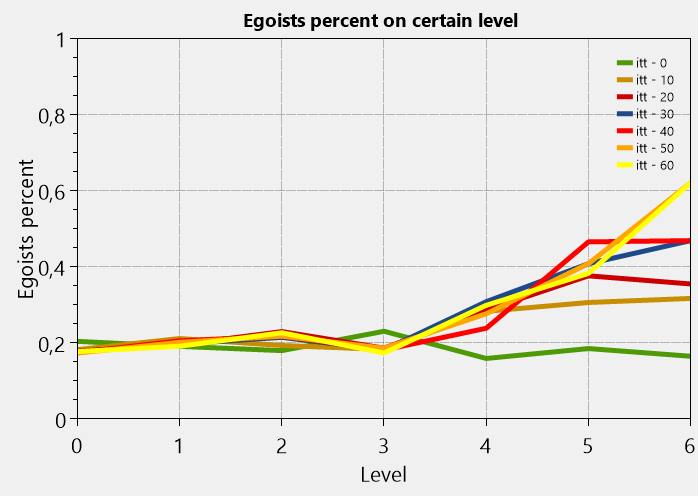
ご覧のように、このような組織では、取締役会のエゴイストの数も増えていますが、利己的なシナリオのようなひどい値にはなりません。さらに、プロセスは最高レベルで1に収束しません。したがって、利己主義の優位性による生産性の低下は大幅に低くなります。わがままなバージョンのように、0.04までではなく、0.06まで。

汎化と信頼区間

ランダムプロセスの異なる実現に応じて、これらのグラフがどの程度正確に変化するかについて、いくつかの質問があるかもしれません。多分、エゴイズムと混合バージョンの間に大きな違いはないのでしょうか？できるだけ2つの異なる実装。

このため、各シナリオは同じパラメーターで20回実行されました。その後、各プロセスの平均の信頼区間でグラフが作成されました。グラフ上の結果。

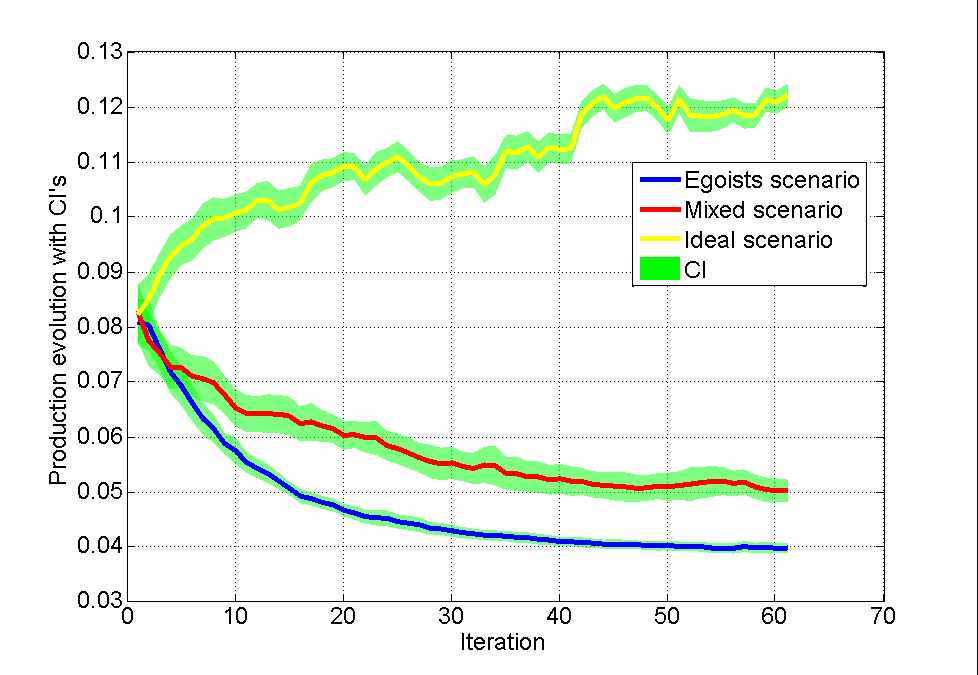
これらの依存関係の多くの興味深い機能に注目することができます。

利己的なシナリオの信頼区間は、他の場合よりも狭くなります。これは、2回目の反復後のプロセスが非常に均一であるためです。ランダムなパフォーマンス特性を持つかなりの数の人々は、すべての部下の生産性の低下を保証するよりも高いレベルに落ちます。これは、一方では、彼らが以前よりもさらに割れるほど利己的だからです。一方、グラフには従属グリッドのかなり広い分岐と一貫性があり、エゴイストが階層の上位の新しい場所への「競合」の一部に陥る可能性が高くなります。そして、各レベルで、この確率は、上位レベルが最も必死のエゴイストで満たされるまでますます増えています。この時点で、プロセスは収束し始めます。

混合バリアントの信頼区間が広い理由は、この構造では、非効率的な生産チェーンを生成するエゴイストを最高レベルの人事異動が非常に迅速に「排除」するためです。男は勝手にトップレベルに到達し、何も彼を邪魔しませんでした。そして突然（別の増加の後）彼の決定は膨大な数の部下の仕事を無効にしました。そして、次の反復では、この人は比較的生産的な相手の昇進に勝ちません。そして、これが起こると、改善はかなり急激に起こります。これは特別な場合のチャートで見ることができます（しかし、時々同じように減少します）。原則として、スキーム自体は直接理想的ではありませんが、エゴイズムとは大きな違いがあります。

結論

従業員の管理されていない昇進は、企業に重大な損害を与え、品質の低下と効率の低下につながる可能性があります。上に示したように、人事ローテーションのために企業が選択したアルゴリズムは、組織全体の作業に大きな影響を与えます。

この記事では、これまで誰も気付かなかった問題を読者が見たり見たりする機会を読者に提供し、適用される問題としてそれを定式化することを試みました。

しかし、新しいレベルの従業員でのみ効果的な昇進を伴う理想主義的なモデルが現実的ではないことは明らかです。問題はすでに質問、どのように理解するかで始まります-従業員は新しい役職で効果的になりますか？彼女の彼の才能は何ですか？したがって、この段階では、状況を最適化する方法に関するアドバイスを行う権利はありません。特定の実際の構造へのモデル実装の転送は常に非常にデリケートなものであり、そのような転送の有効性のかなりの量の実用的なチェックと証拠が必要です。

ただし、最後に、2010年にイタリアの研究者にシュノベル賞が授与されたことを思い出してください。ピーターの原則を使用して、最も効果的な昇進アルゴリズム（この原則が現実に適切な場合）は、ランダムジェネレーターによって選択されたランダムな従業員を昇進させることであると証明しました数字すでに完全にランダムで、おそらくそれだけの価値はありませんが、おそらくショートリストからランダムを選択する方が便利でしょう。しかし、これは正確ではありません。

記事の著者：Alexander Bespalov、データサイエンティスト、Maxilect

PS私たちはいくつかのrunetサイトに記事を公開しています。 VK 、 FB、または電報チャネルのページを購読して、すべての出版物およびその他のMaxilectニュースについて学びます。

企業の階層構造における従業員の負の選択

エントリー

モデルの説明

シミュレーション中はどうなりますか？

汎化と信頼区間

結論

More articles: