政治的イベントのクラスタリングの問題における自動エンコーダー

数年連続で、機械学習アルゴリズムがさまざまな分野で使用されてきました。 そのような分野の1つは、政治分野のさまざまなイベントの分析です。たとえば、投票結果の予測、行われた意思決定をクラスタリングするメカニズムの開発、政治関係者の活動の分析などです。 この記事では、この分野の研究の1つの結果を共有しようとします。

問題の声明

最新の機械学習ツールを使用すると、大量のデータを変換して視覚化できます。 この事実により、4年間の投票を各議員の行動を表すポイントの自己組織化空間に変換することにより、政党の活動を分析することが可能になりました。



各政治家は、12,000票の事実を表明しています。 各投票には、5つのオプションのいずれかを選択できます（ホールに来なかった、来たが投票に失敗した、「賛成」、「反対」、または棄権）。



私たちのタスクは、すべての投票結果を特定のバランスの取れた位置を反映する3次元ユークリッド空間のポイントに変換することです。

オープンデータ

すべての初期データは公式Webサイトで取得され、ニューラルネットワークのデータに変換されました。

オートエンコーダー

問題の声明からわかるように、12,000票を次元2または3のベクトルとして提示する必要があります。人が操作できる2次元および3次元の空間のカテゴリがあるため、多くの空間は人が想像するのが非常に困難です。



ビット深度を減らすために、自動エンコーダーを使用します。







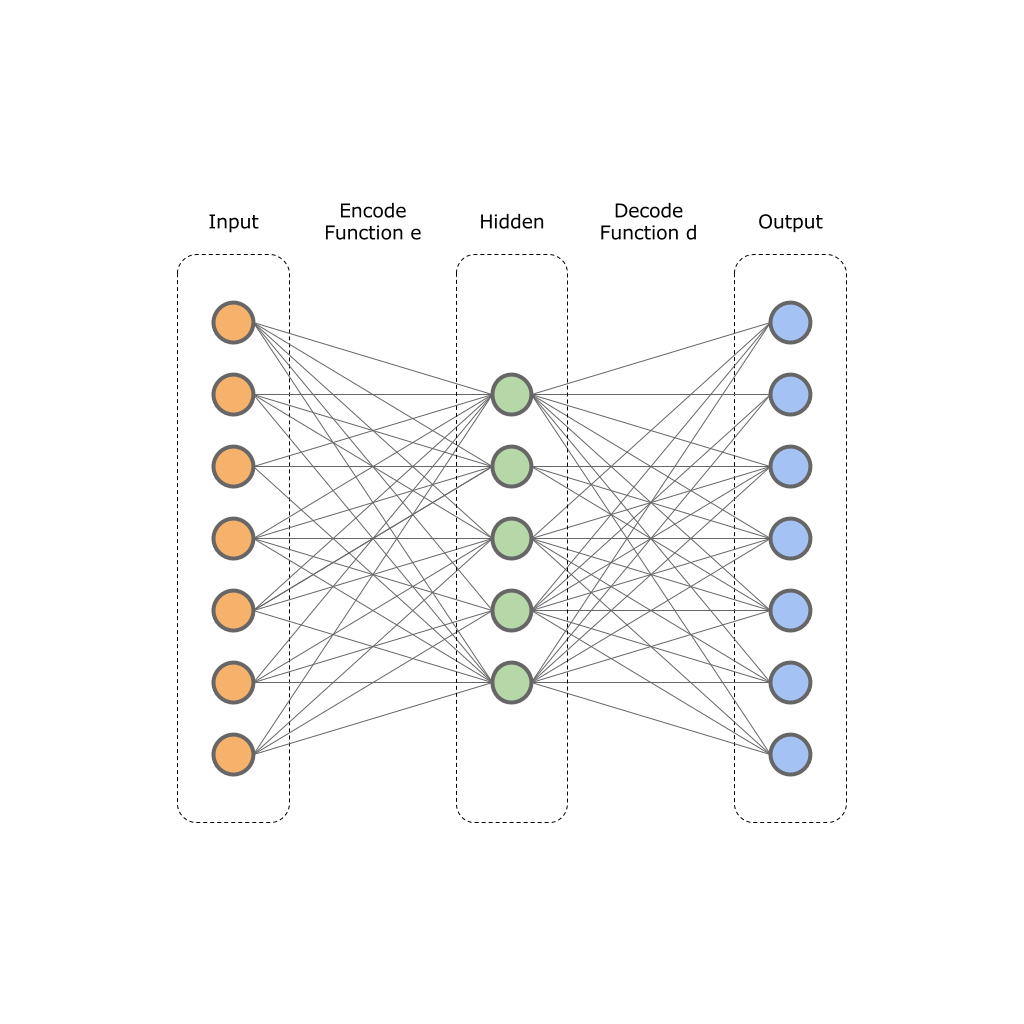
自動エンコーダーの基礎は、2つの機能の原理を確立しました。



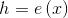-関数エンコーダー;



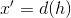-関数デコーダー;



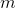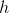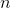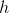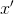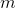元のベクトルは、このようなネットワークの入力に供給されます。 寸法 そしてニューラルネットワークはそれを隠れ層の値に変換します 寸法 。 次に、ニューラルネットワークデコーダーが隠れ層の値を変換します 出力ベクトル内 寸法 しながら 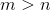。 つまり、非表示レイヤーはより小さな次元になりますが、同時にソースデータのセット全体を反映することができます。



ネットワークを訓練するために、客観的誤差関数が使用されます：







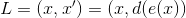
つまり、入力レイヤーと出力レイヤーの値の差を最小限に抑えます。 訓練されたニューラルネットワークにより、元のデータの次元を特定の次元に圧縮できます。 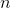隠しレイヤー 。



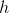この画像は、1つの入力、1つの非表示、1つの出力レイヤーを示しています。 実際には、このような層がさらに存在する場合があります。



私は理論を伝えようとしましたが、実践に移りましょう。



データはすでに公式サイトからJSON形式で収集され、ベクトルでエンコードされています。







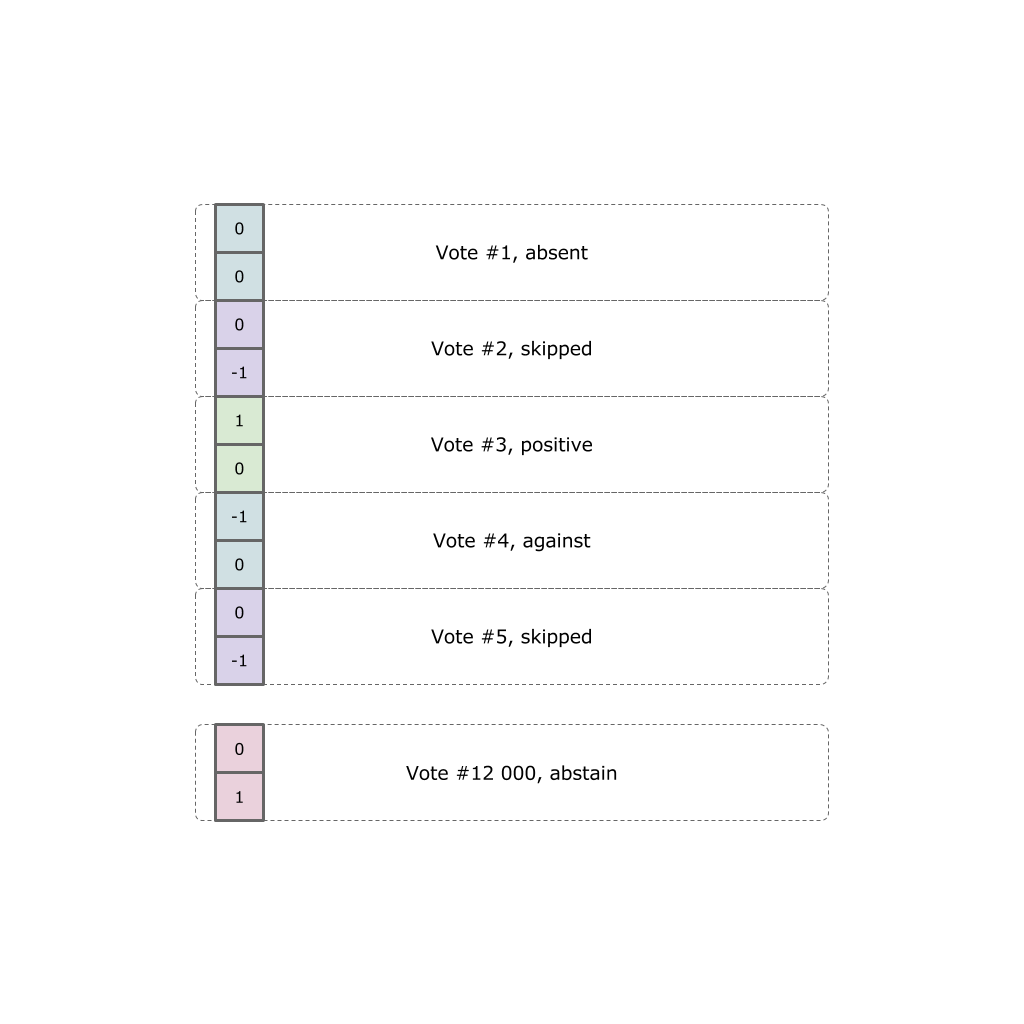
これで、ディメンションが24000 x 453のデータセットができました。TensorFlowを使用してニューラルネットワークを作成します。

# Building the encoder def encoder(x): with tf.variable_scope('encoder', reuse=False): with tf.variable_scope('layer_1', reuse=False): w1 = tf.Variable(tf.random_normal([num_input, num_hidden_1]), name="w1") b1 = tf.Variable(tf.random_normal([num_hidden_1]), name="b1") # Encoder Hidden layer with sigmoid activation #1 layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, w1), b1)) with tf.variable_scope('layer_2', reuse=False): w2 = tf.Variable(tf.random_normal([num_hidden_1, num_hidden_2]), name="w2") b2 = tf.Variable(tf.random_normal([num_hidden_2]), name="b2") # Encoder Hidden layer with sigmoid activation #2 layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, w2), b2)) with tf.variable_scope('layer_3', reuse=False): w2 = tf.Variable(tf.random_normal([num_hidden_2, num_hidden_3]), name="w2") b2 = tf.Variable(tf.random_normal([num_hidden_3]), name="b2") # Encoder Hidden layer with sigmoid activation #2 layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, w2), b2)) return layer_3 # Building the decoder def decoder(x): with tf.variable_scope('decoder', reuse=False): with tf.variable_scope('layer_1', reuse=False): w1 = tf.Variable(tf.random_normal([num_hidden_3, num_hidden_2]), name="w1") b1 = tf.Variable(tf.random_normal([num_hidden_2]), name="b1") # Decoder Hidden layer with sigmoid activation #1 layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, w1), b1)) with tf.variable_scope('layer_2', reuse=False): w1 = tf.Variable(tf.random_normal([num_hidden_2, num_hidden_1]), name="w1") b1 = tf.Variable(tf.random_normal([num_hidden_1]), name="b1") # Decoder Hidden layer with sigmoid activation #1 layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, w1), b1)) with tf.variable_scope('layer_3', reuse=False): w2 = tf.Variable(tf.random_normal([num_hidden_1, num_input]), name="w2") b2 = tf.Variable(tf.random_normal([num_input]), name="2") # Decoder Hidden layer with sigmoid activation #2 layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, w2), b2)) return layer_3 # Construct model encoder_op = encoder(X) decoder_op = decoder(encoder_op) # Prediction y_pred = decoder_op # Targets (Labels) are the input data. y_true = X # Define loss and optimizer, minimize the squared error loss = tf.reduce_mean(tf.pow(y_true - y_pred, 2)) tf.summary.scalar("loss", loss) optimizer = tf.train.RMSPropOptimizer(learning_rate).minimize(loss)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

自動エンコーダーの完全なリスト。



ネットワークは、0.01のステップでRMSProbオプティマイザーによってトレーニングされます。

その結果、TensorFlow操作グラフを見ることができます。







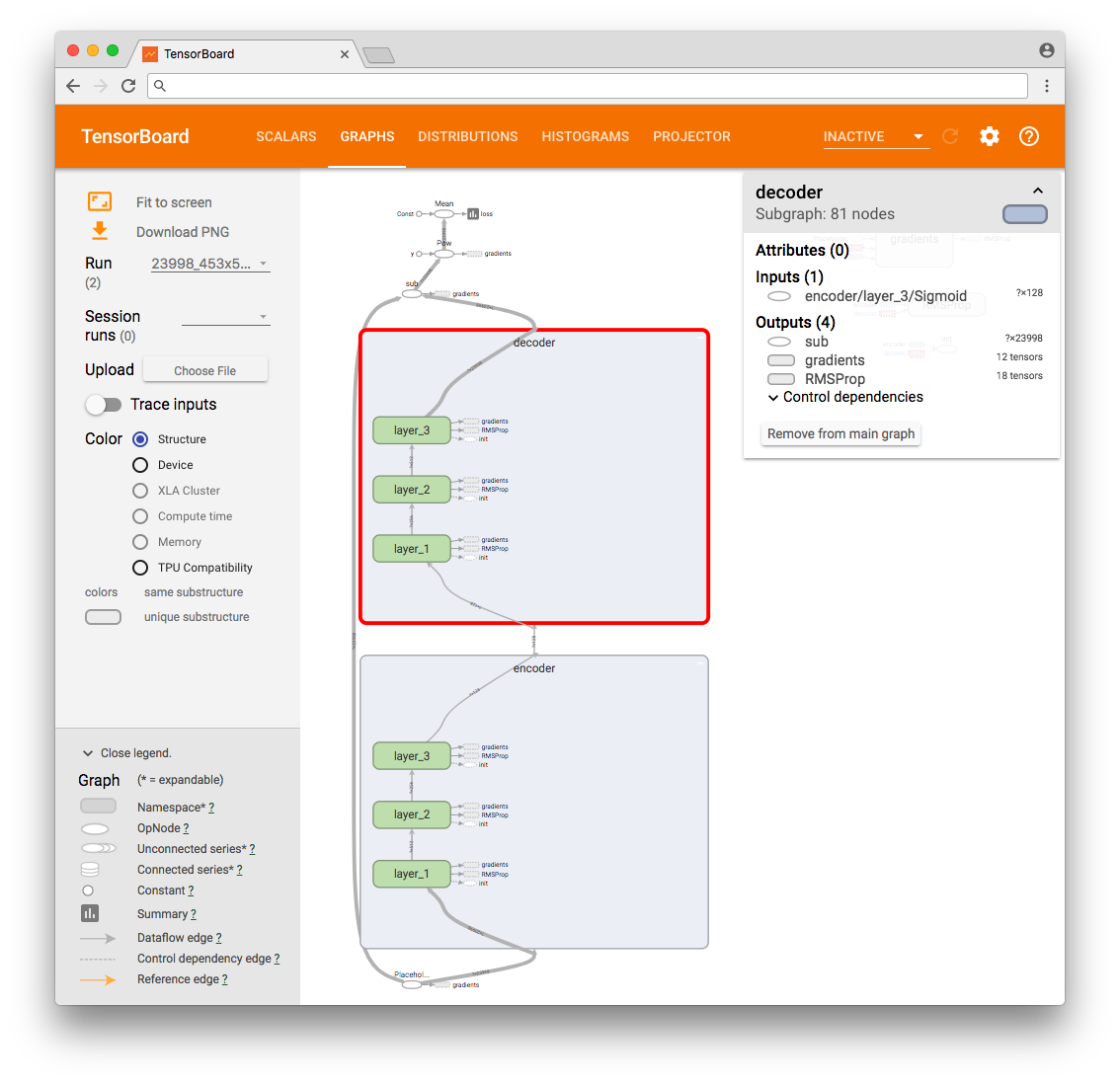
追加のテストのために、最初の4つのベクトルを選択し、ネットワーク入力および出力でそれらの値を画像形式で解釈します。 そのため、出力層の値が入力層の値と「同一」（エラーあり）であることを視覚的に確認できます。





元の入力。



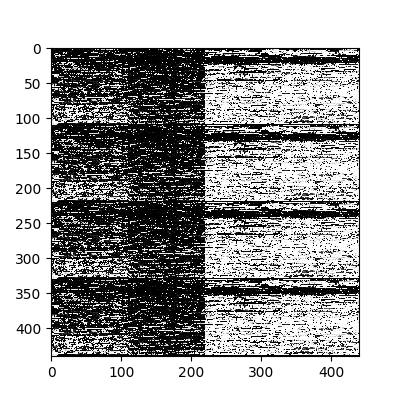
ニューラルネットワークの出力層の値。



その後、すべての初期データをネットワークに順次転送し、隠れ層の値を抽出します。 これらの値は、目的の圧縮データになります。



ちなみに、さまざまなレイヤーをピックアップして、最小エラーに近づけることができる構成を選択しました。



PCAおよびt-SNA次元減速機。

この段階では、寸法が64のベクトルが450個あります。これはすでに非常に良い結果ですが、人に与えるには十分ではありません。 このため、「私たちはより深く行きます」。 PCAとt-SNAのダウングレードアプローチを使用します。 主成分分析（PCA）方法について多くの記事が書かれているので、その分析については触れませんが、t-SNAアプローチについてお話したいと思います。



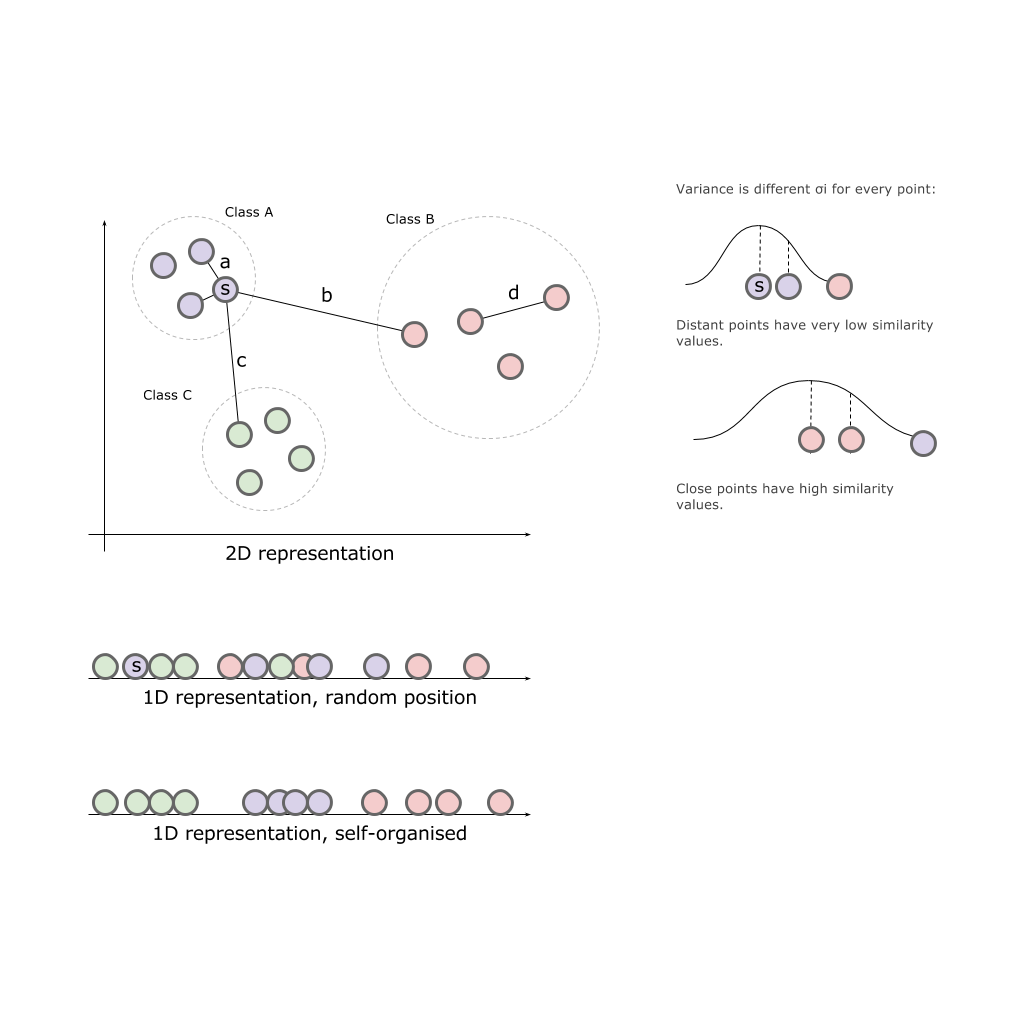
t-SNEドキュメントを使用した元の視覚化データには、アルゴリズムの詳細な説明が含まれています 。たとえば、2次元を1次元に縮小するオプションを検討します。



2次元空間と、この空間に配置された3つのクラスA、B、Cを使用して、いずれかの軸にクラスを投影します。





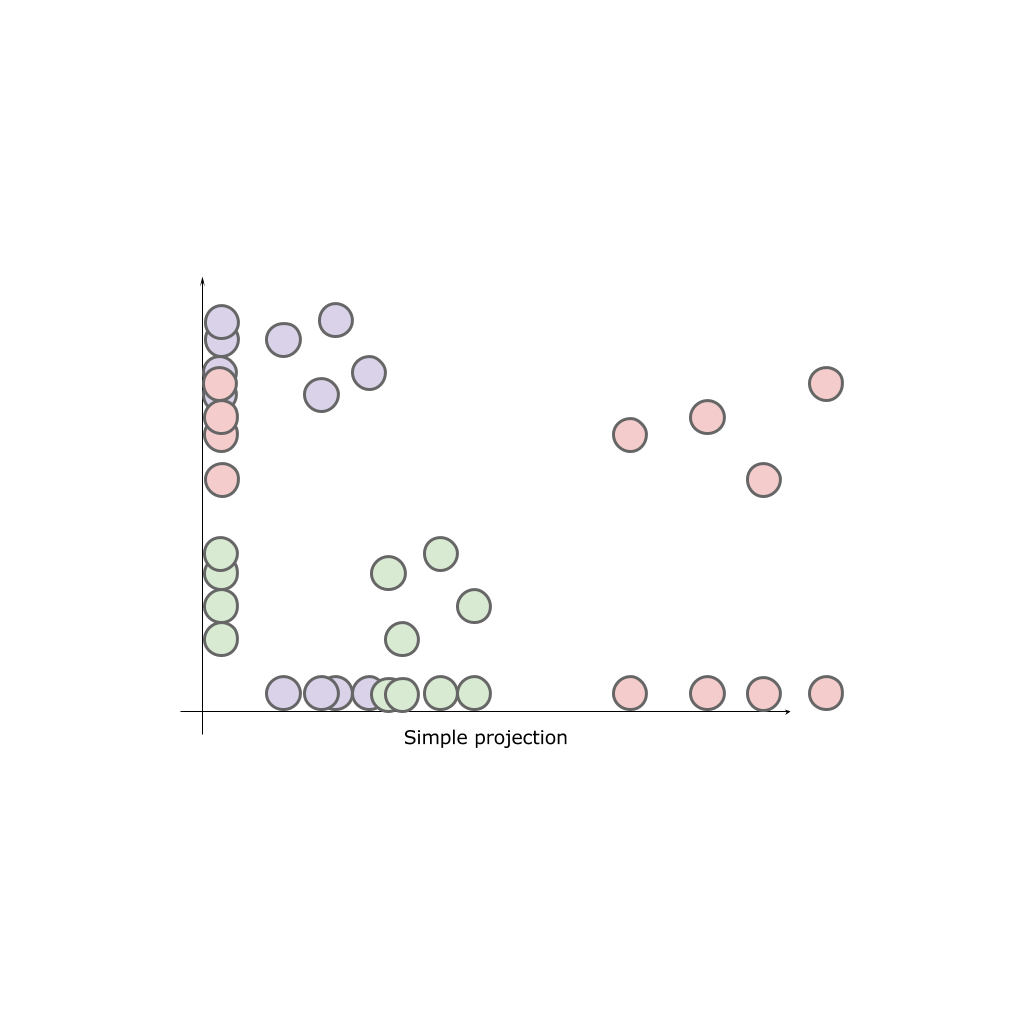
結果として、どの軸もソースクラスの全体像を提供できません。 クラスは「ミックス」します。つまり、自然の特性が失われます。



私たちのタスクは、元の空間に配置された方法に比例して（おおよそ）有限の空間に要素を配置することです。 つまり、互いに近くにあるものは、遠くにあるものよりも近くにある必要があります。

確率的近傍埋め込み

初期空間における点間の初期関係を、点間のユークリッド空間における距離として表現しましょう 、 ：

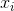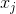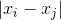それに応じて 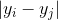目的の空間内のポイント。



ソース空間内のポイントの類似性を表す条件付き確率を定義します。







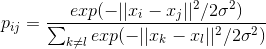
この式は、ポイントがどれだけ近いかを特徴付けます。 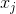ポイントまで 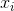ただし、クラスの最も近い点までの距離を、周囲のガウス分布として特徴付ければ 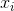与えられた分散で （中心点 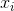） 分散は各ポイントに固有であり、密度の高いポイントは分散が低いという事実に基づいて個別に計算されます。



次に、ポイントの類似性について説明します 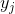ドット付き 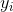それぞれ新しいスペースで：







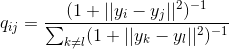
繰り返しますが、ペアワイズの類似性のモデリングにのみ関心があるため、 。

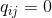表示ポイントの場合 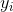そして 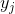高次元データポイント間の類似性を正しくシミュレートする 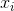そして 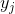条件付き確率 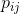そして 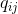等しくなります。 この観察によって動機付けられたSNEは、データの低次元表現を見つけ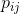て、 そして 。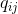

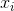アルゴリズムは分散値を見つけます 特定の各点でのガウス分布 。 一つの意味があるとは考えにくい 、データ密度が変化する可能性があるため、データセットのすべてのポイントに最適です。 密集地域では、低い値 通常、より疎な地域よりも適切です。 SNEはバイナリ検索を使用して選択します 。

検索は、計算時に考慮される有効な近隣の測定値（perplexityパラメーター）を考慮に入れると発生します 。

アルゴリズムの作成者は物理学の例を見つけ、このアルゴリズムを、他のオブジェクトを引き付けて反発できるさまざまなバネを持つオブジェクトの束として説明しています。 システムをしばらく放置すると、すべてのスプリングの張力のバランスを取ることにより、独立して休憩ポイントを見つけます。

t分布の確率的近傍埋め込み

SNEとt-SNEアルゴリズムの違いは、ガウス分布をスチューデント分布（別名t-Distribution、t-Student分布）に置き換え、誤差関数を対称分布に変更することです。



したがって、アルゴリズムは最初にすべてのソースオブジェクトを低次元の空間に配置します。 オブジェクトがオブジェクトの背後に移動し始めた後、元の空間内の他のオブジェクトとの距離（近く）に依存します。

TensorFlow、TensorBoard、およびプロジェクター

現在、このようなアルゴリズムを自分で実装する必要はありません。 既製の数学パッケージscikit 、 matlabまたはTensorFlowを使用できます。



TensorFlowツールキットには、データの視覚化とTensorBoardの学習プロセスのためのパッケージが含まれていることを以前の記事で書きました 。



したがって、この特定のソリューションを使用します。

 import os import numpy as np import tensorflow as tf from tensorflow.contrib.tensorboard.plugins import projector # Create randomly initialized embedding weights which will be trained. first_D = 23998 # Number of items (size). second_D = 11999 # Number of items (size). DATA_DIR = '' LOG_DIR = DATA_DIR + 'embedding/' first_rada_input = np.loadtxt(DATA_DIR + 'result_' + str(first_D) + '/rada_full_packed.tsv', delimiter='\t') second_rada_input = np.loadtxt(DATA_DIR + 'result_' + str(second_D) + '/rada_full_packed.tsv', delimiter='\t') first_embedding_var = tf.Variable(first_rada_input, name='politicians_embedding_' + str(first_D)) second_embedding_var = tf.Variable(second_rada_input, name='politicians_embedding_' + str(second_D)) saver = tf.train.Saver() with tf.Session() as session: session.run(tf.global_variables_initializer()) saver.save(session, os.path.join(LOG_DIR, "model.ckpt"), 0) config = projector.ProjectorConfig() # You can add multiple embeddings. Here we add only one. first_embedding = config.embeddings.add() second_embedding = config.embeddings.add() first_embedding.tensor_name = first_embedding_var.name second_embedding.tensor_name = second_embedding_var.name # Link this tensor to its metadata file (eg labels). first_embedding.metadata_path = os.path.join(DATA_DIR, '../rada_full_packed_labels.tsv') second_embedding.metadata_path = os.path.join(DATA_DIR, '../rada_full_packed_labels.tsv') first_embedding.bookmarks_path = = os.path.join(DATA_DIR, '../result_23998/bookmarks.txt') second_embedding.bookmarks_path = = os.path.join(DATA_DIR, '../result_11999/bookmarks.txt') # Use the same LOG_DIR where you stored your checkpoint. summary_writer = tf.summary.FileWriter(LOG_DIR) # The next line writes a projector_config.pbtxt in the LOG_DIR. TensorBoard will # read this file during startup. projector.visualize_embeddings(summary_writer, config)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

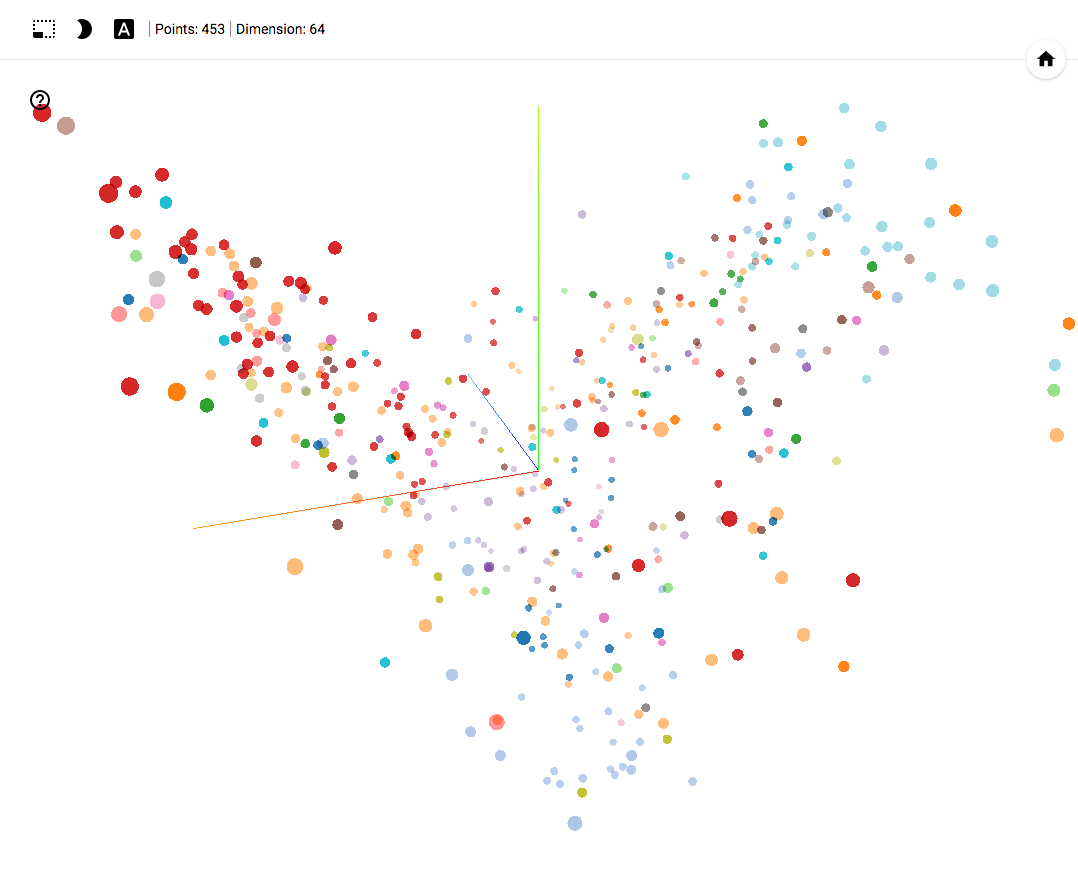
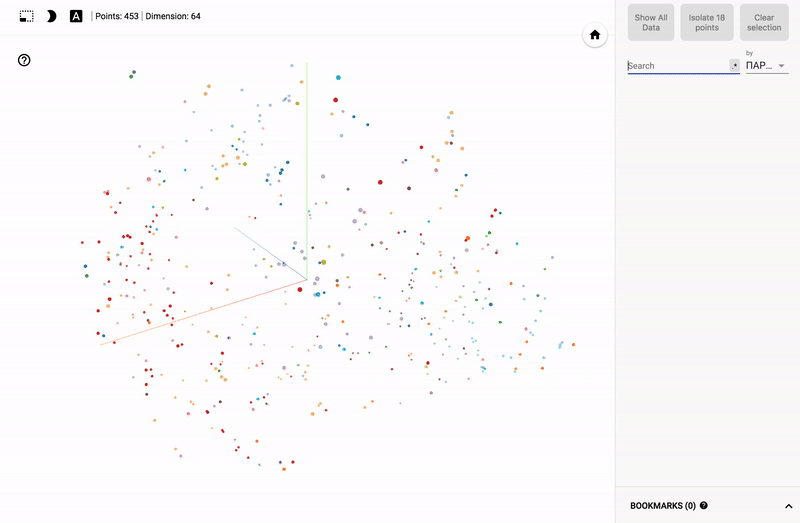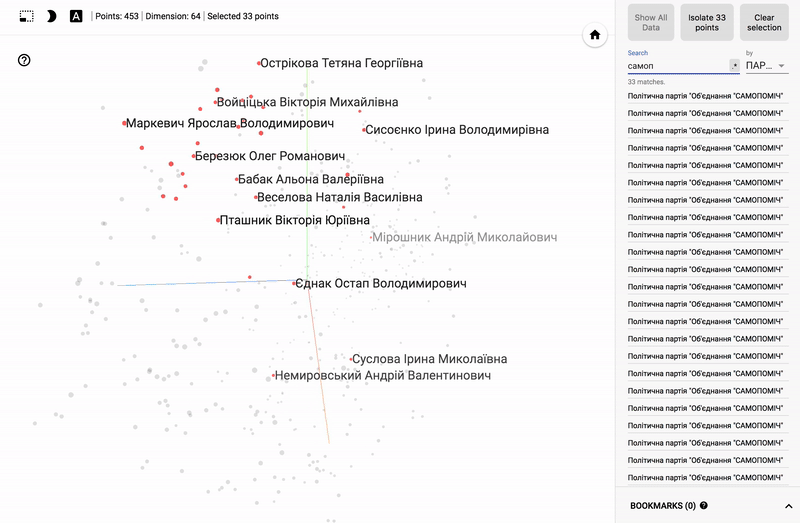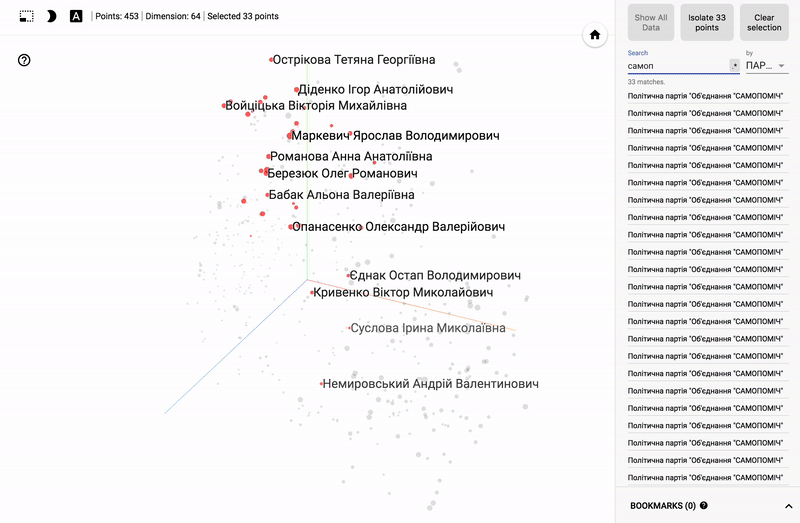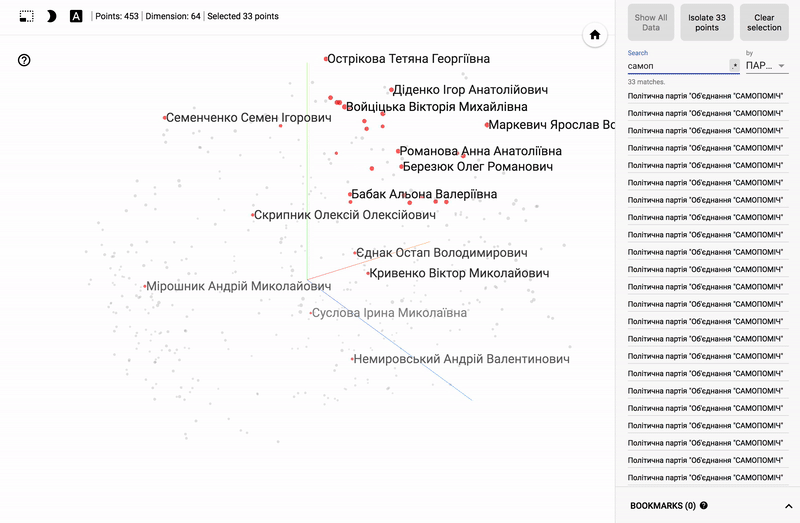
結果は私のTensorBoardプロジェクターで見ることができます。

1. Chromeで動作します。
2. 右下隅のブックマークを開いてクリックします。
3. 右上隅で、クラスをフィルタリングできます。
4. 以下はGIF画像と例です。

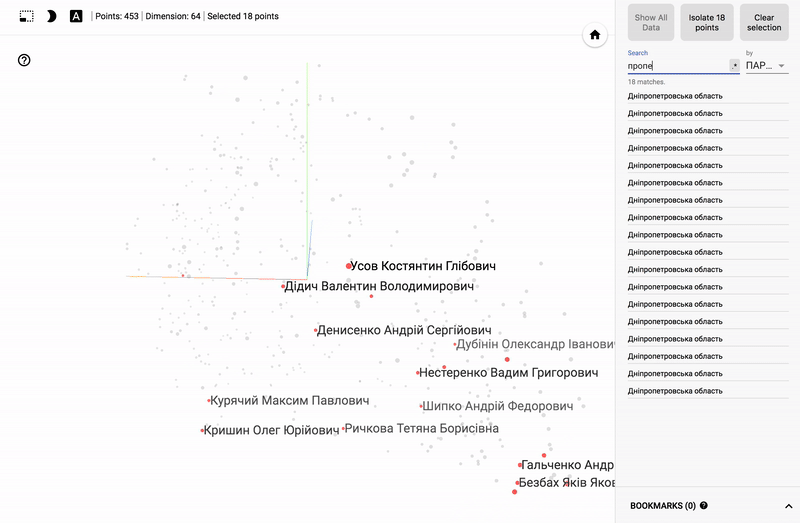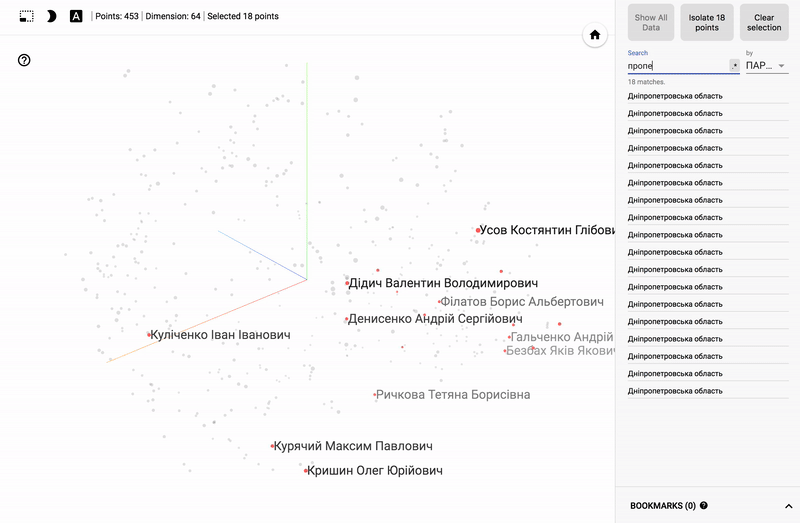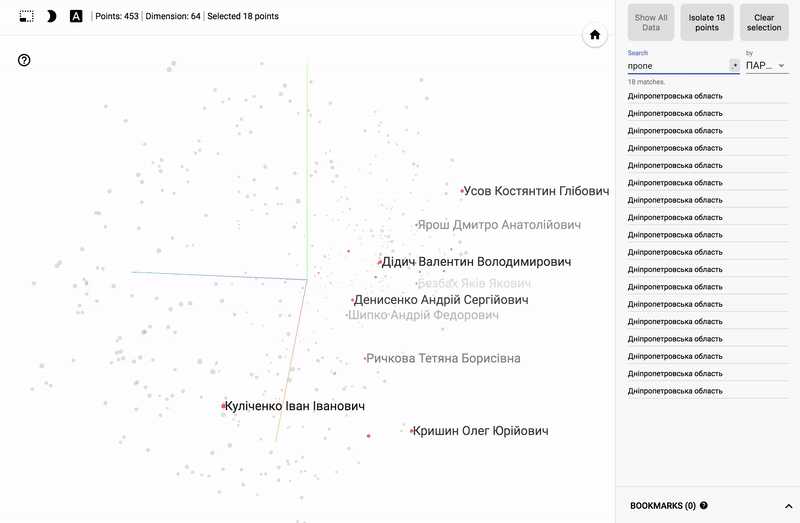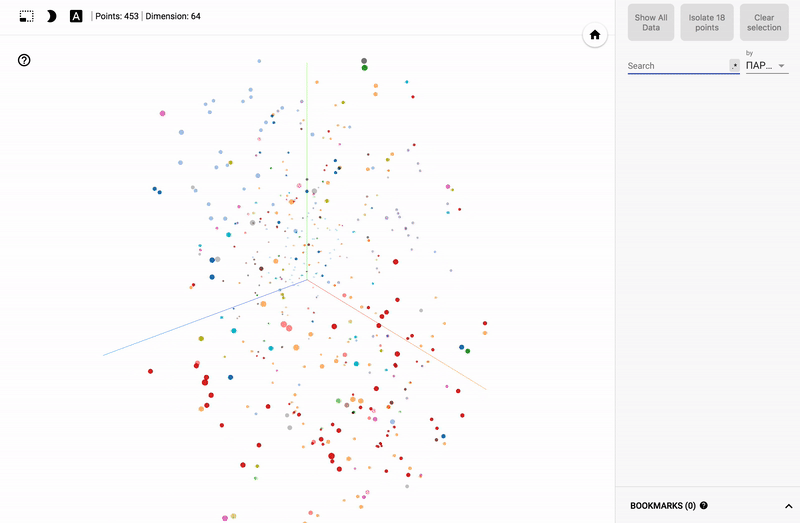
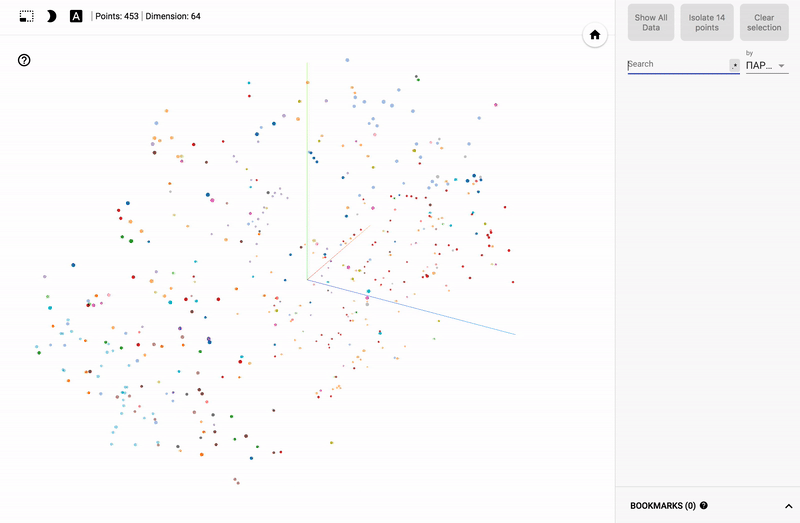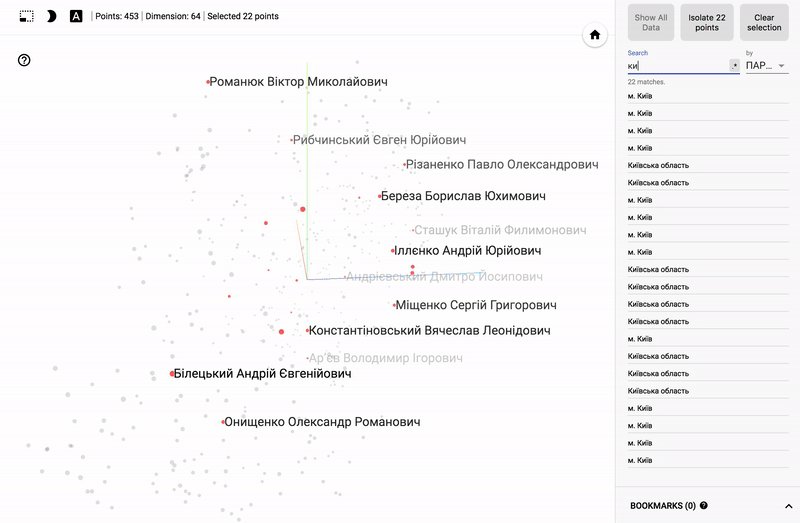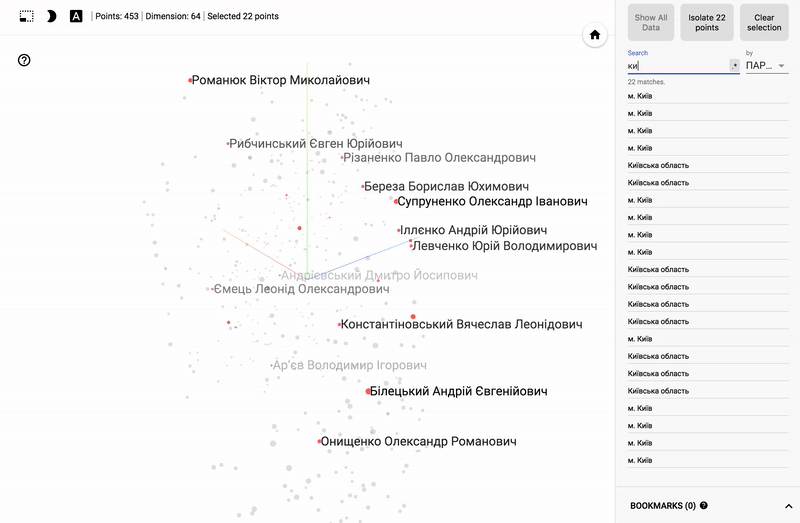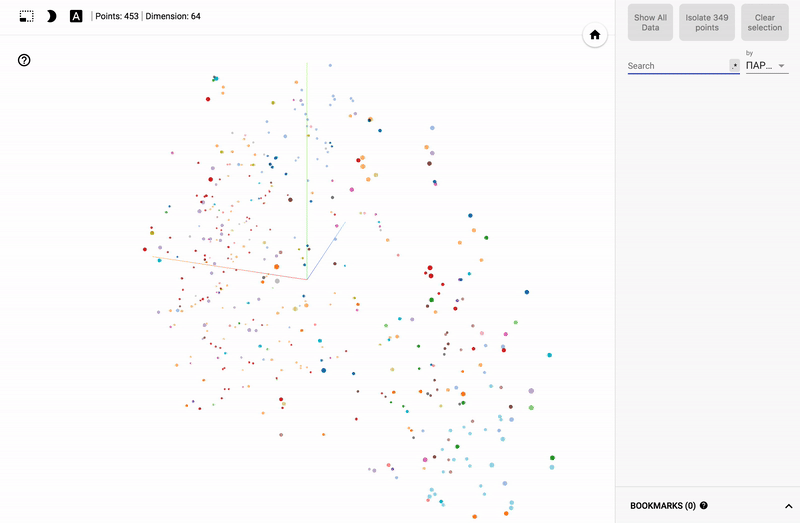
また、ポータル全体が利用可能になりました- プロジェクターを使用すると、Googleサーバー上でデータセットを直接視覚化できます。

1. プロジェクターのWebサイトにアクセスします
2. 「データの読み込み」をクリックします
3. ベクトルを使用してデータセットを選択する
4. 事前に収集したメタデータを追加します：ラベル、クラスなど。
5. 列の1つに従って色の区別（カラーマップ）を接続します。
6. 必要に応じて、json構成ファイルを追加し、データを公開して公開します。

リンクをアナリストに送信することは残っています。



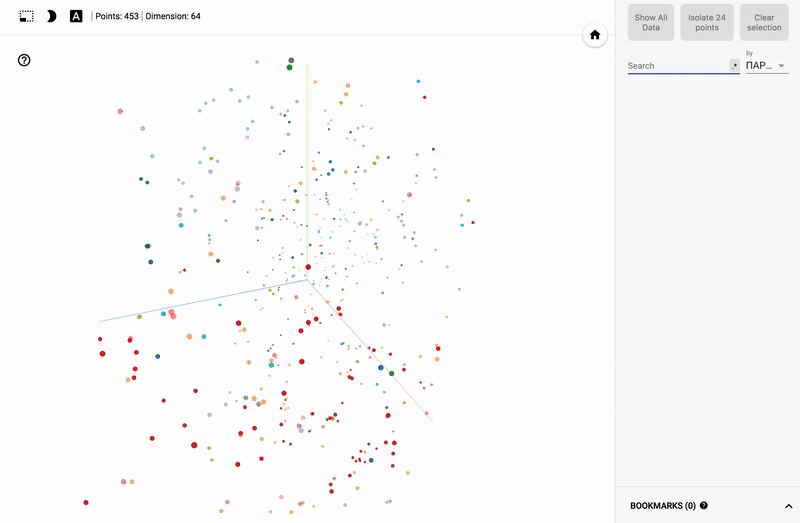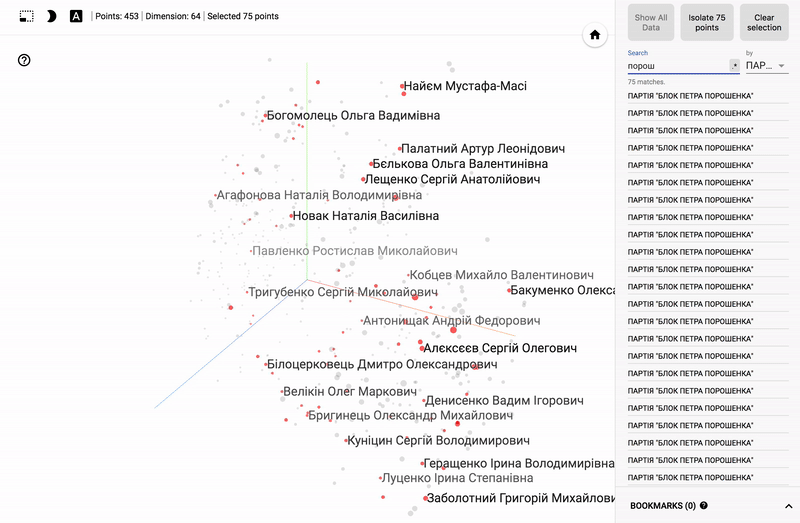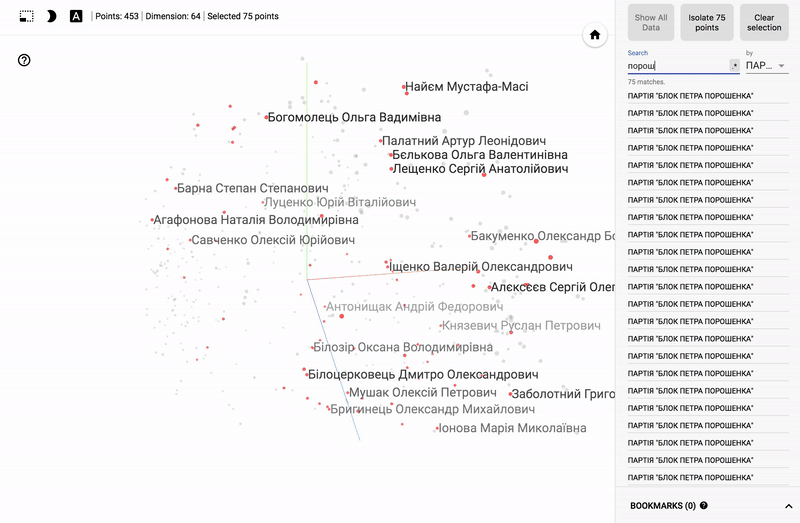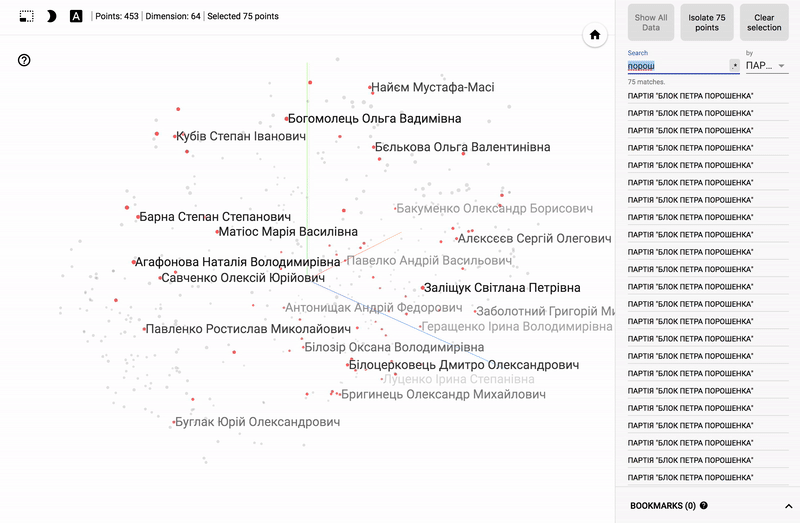
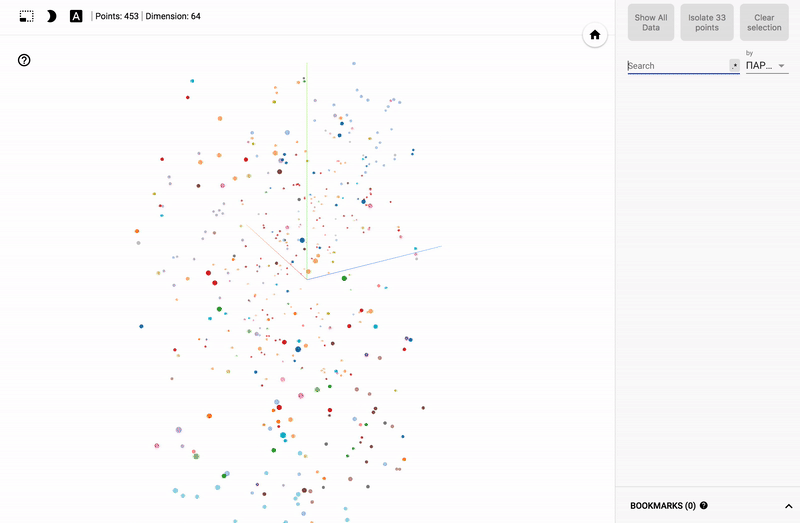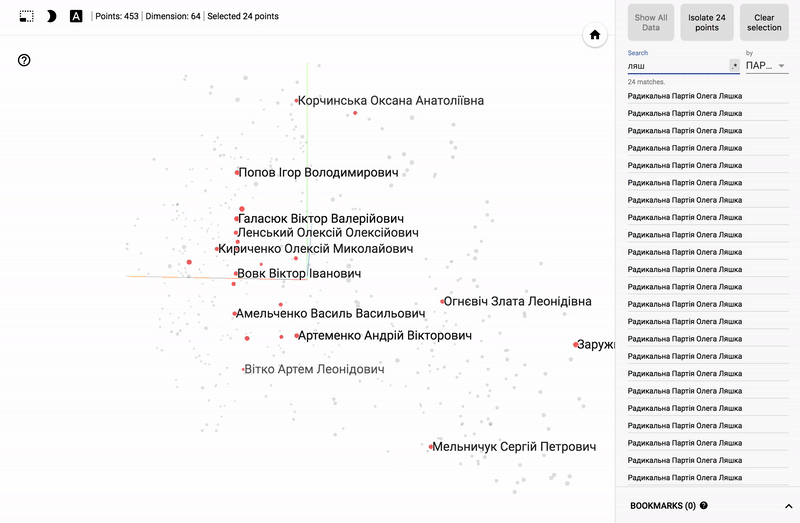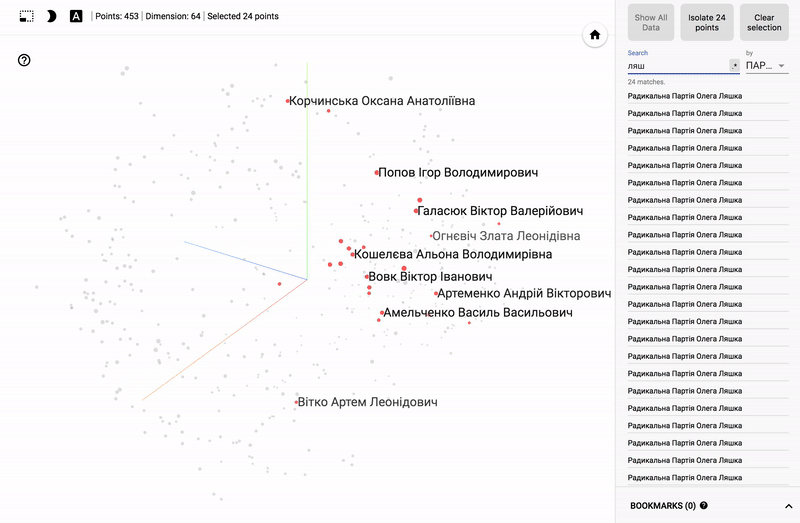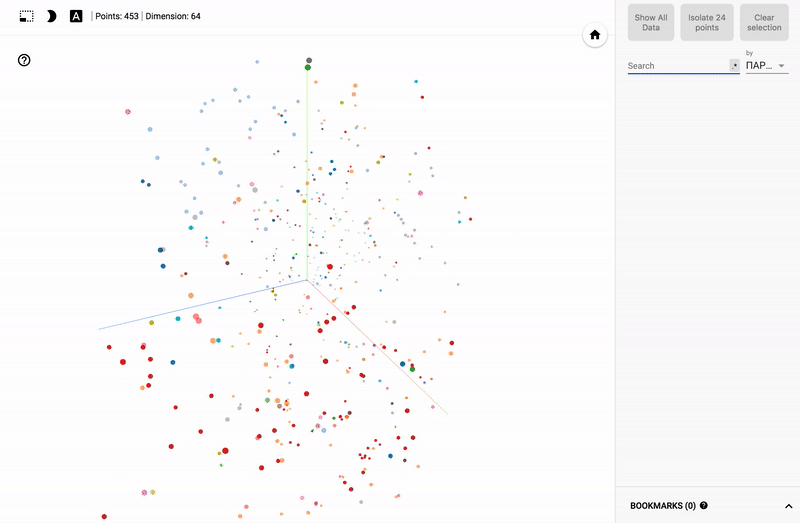
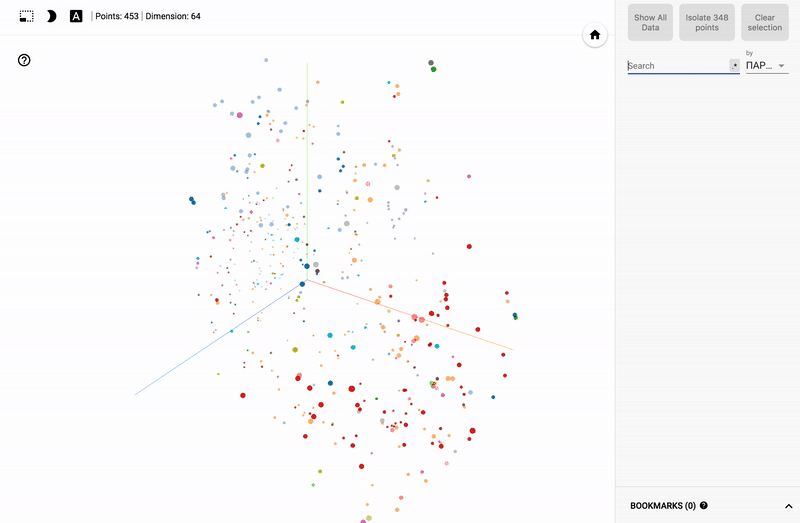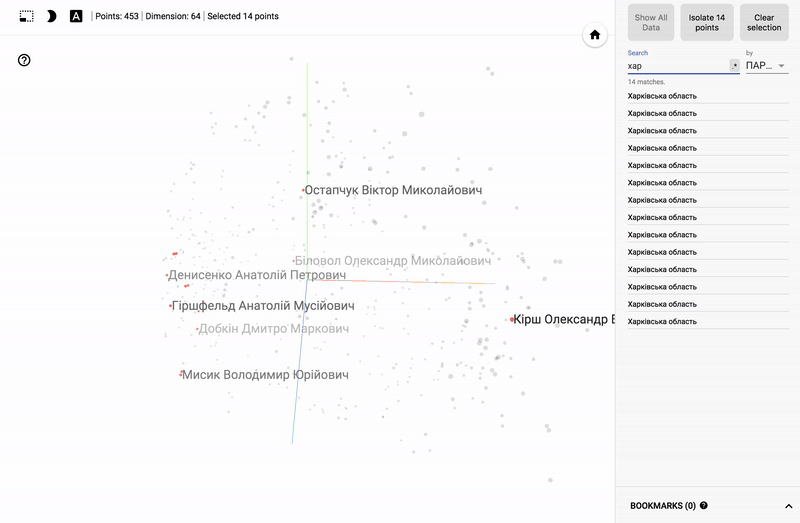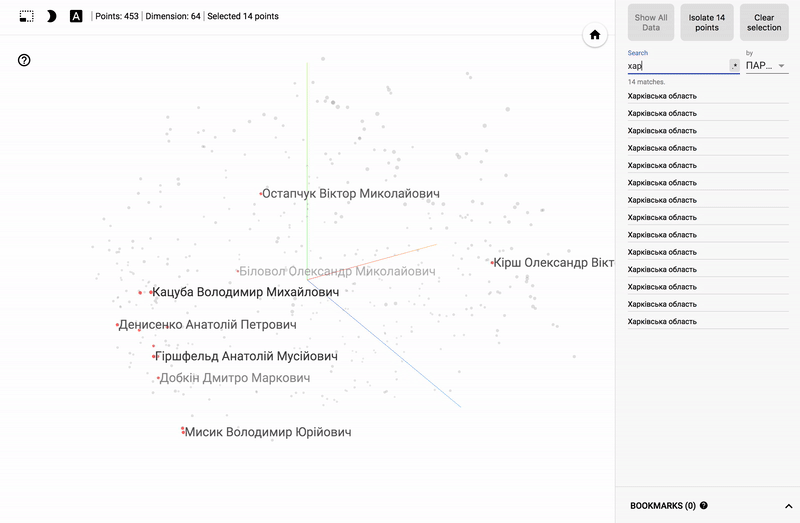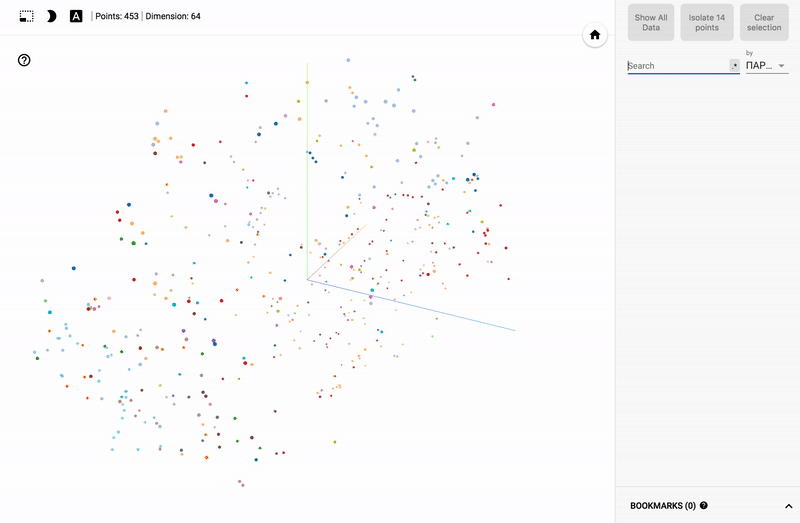
主題分野に興味がある人にとっては、例えば、さまざまな分野の政治家の世論調査の分布など、さまざまなセクションを見るのは興味深いでしょう。

• 個々の政党の投票の正確さ。
• ある政党からの政治家の分布（スミアリング）。
• 異なる政党からの政治家の投票の類似性。

結論

• 自動エンコーダーは、驚くほど高速で優れた収束結果をもたらす比較的単純なアルゴリズムのファミリーです。
• 自動クラスタリングは、ソースデータの性質に関する質問に対する答えではなく、追加の分析が必要ですが、データの操作を開始できるかなり迅速かつ明確なベクトルを提供します。
• TensorFlowとTensorBoardは、さまざまな複雑さの問題を解決するための強力で急速に成長している機械学習ツールです。