私はロボット研究者であり、同時に私の趣味はゲーム開発です。 私の専門は、ロボットアームの多次元運動を計画することです。 モーションプランニングはゲーム開発者にとって非常に重要なトピックであり、制御されたAIキャラクターをあるポイントから別のポイントに移動する必要があるたびに役立ちます。



ゲーム開発を研究する過程で、私は交通計画について話している多くのチュートリアルを見つけました（通常、ゲーム開発に関する文献では「道を見つける」と呼ばれています）。 。 私が知る限り、ほとんどのゲームは3つの深刻なアルゴリズムの1つを除いて、他のモーションプランニングをほとんど使用しません：A *グリッド、可視性グラフ、フローフィールドでの検索。 これらの3つの原則に加えて、モーションプランニングの理論的研究の世界がまだあり、それらのいくつかはゲーム開発者に役立つかもしれません。



この記事では、私のコンテキストで標準的なトラフィック計画手法について説明し、その利点と欠点を説明します。 また、ビデオゲームでは一般的に使用されない基本的なテクニックも紹介します。 彼らがゲーム開発にどのように適用できるかを明らかにすることを願っています。

ポイントAからポイントBへの移動：エージェントと目標

ゲームにAI制御のキャラクターがいるという事実から始めましょう。たとえば、シューティングゲームの敵や戦略ゲームのユニットなどです。 このキャラクターをエージェントと呼びます。 エージェントは、「構成」と呼ばれる世界の特定の場所にあります。 2次元では、エージェント構成は2つの数字（通常はxとy）で表すことができます。 エージェントは、世界の他の場所に到達したいので、これを目標（ゴール）と呼びます。



エージェントを平らな2次元の世界に住む円として想像してみましょう。 エージェントが必要な方向に移動できると仮定します。 エージェントとそのターゲットの間に空きスペースしかない場合、エージェントは現在の構成からターゲットまで直線的に移動できます。 彼が目標に到達すると、彼は停止します。 これを「Walk Toアルゴリズム」と呼ぶことができます。



: WALK TO

1. :
   
   
   
   
   1. .
      
      
      
      
2. : .
   
   
   
   

世界が完全に空の場合、これは完全に適合します。 初期設定からターゲット設定に移動する必要があることは明らかなように思えるかもしれませんが、エージェントが現在の設定からターゲットに到達するためにまったく異なる方法で移動できることを考慮する価値があります。 彼はゴールに到達するまでサイクルを繰り返すか、ゴールから50キロメートル離れてからゴールに戻り、ゴールで止まります。



では、なぜ直線が明らかなのでしょうか？ ある意味で、これが「最良の」移動方法だからです。 エージェントが任意の方向に一定の速度でしか移動できないと仮定すると、直線はある地点から別の地点に到達するための最短かつ最速の方法です。 この意味で、Walk Toアルゴリズムは最適です。 この記事では、最適性について詳しく説明します。 実際、アルゴリズムの最適性について話すとき、それは「最高」という特定の基準を持つ「すべての最高」であることを意味します。 できるだけ早くポイントAからポイントBに到達したいが、途中に何もない場合は、直線と比較することはできません。



実際、多くのゲームでは（ ほとんどのゲームでも）、Walk To直線アルゴリズムは問題を解決するのに理想的です。 迷路を歩き回ったり、プレイヤーの指示に従う必要のない廊下や部屋に小さな2D敵がいる場合、これ以上複雑なものは必要ありません。



しかし、何かが途中で突然現れた場合はどうなりますか？









この場合、パス上のオブジェクト（障害物と呼ばれる）は、エージェントのターゲットへのパスをブロックします。 エージェントはターゲットに直接移動できなくなるため、停止します。 ここで何が起こったのですか？



Walk Toアルゴリズムは最適ですが 、 完全ではありません。 「完全な」アルゴリズムは、限られた時間でその分野のすべての問題を解決することができます。 私たちの場合、エリアは障害物のある平面に沿って移動する円です。 明らかに、単に目標に直接移動するだけでは、この分野のすべての問題が解決されるわけではありません。



この分野のすべての問題を解決し、それらを最適に解決するには、より洗練されたものが必要です。

事後計画：カブトムシアルゴリズム

障害があった場合はどうしますか？ 目標（ドアなど）に到達する必要があり、途中で何か（椅子など）が存在する場合は、単にそれを迂回して目標に向かって動き続けます。 このタイプの動作は、「障害物の回避」と呼ばれます。 この原則は、エージェントをターゲットに移動するという問題を解決するために使用できます。



最も単純な障害物回避アルゴリズムの 1つは、ビートルアルゴリズムです。 次のように機能します。



: BUG

1. . M-.
   
   
   
   
2. M- :
   
   
   
   
   
   
   1. , .
      
      
      
      
   2. , , M-, , M-. M-, 2.
      
      
      
      

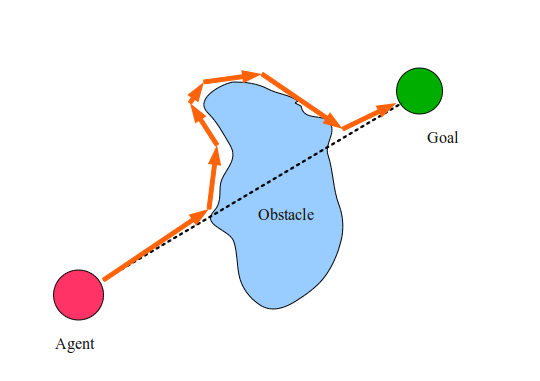
ステップ2.2には説明が必要です。 実際、エージェントは現在の障害物のMラインに遭遇したすべてのケースを記憶し、障害物がMライン上にあり、他のどの時点よりもターゲットに近い場合にのみ障害物を離れます。 これは、エージェントが無限ループに陥ることを避けるためです。



上の図では、破線はMラインを示し、オレンジ色の矢印は目標を達成するためにエージェントが実行するステップを示しています。 それらはエージェントトラジェクトリと呼ばれます。 驚くべきことに、カブトムシのアルゴリズムはこのタイプの多くの問題を非常に簡単に解決します。 たくさんのクレイジーな数字を描いて、それがどのように機能するかを確認してください！ しかし、バグアルゴリズムはすべてのタスクで機能しますか？ そして、なぜそれが機能するのですか？



単純なビートルアルゴリズムには多くの興味深い機能があり、多くの重要な概念を示しています。これについては、この記事で説明します。 これらの概念は次のとおりです。軌跡、政治、ヒューリスティック、完全性、最適性。



軌道の概念についてはすでに述べましたが、これはエージェントが途中で実行する構成または移動の単純なシーケンスです。 バグアルゴリズムは、軌道計画、つまり初期構成とターゲットの構成を受け取り、軌道を最初からターゲットに戻すアルゴリズムと考えることができます。 （ゲーム開発に関する文献では、「パスプランナー」とも呼ばれます）。



しかし、私たちは政治の概念にも言及しなければなりません。 ビートルアルゴリズムを最初からターゲットまで完全な軌道を返すと解釈せず、単に独自の設定をガイドとして使用して、 どこからでもターゲットに到達できる一連の指示をエージェントに送信すると解釈する場合、ビートルアルゴリズムは制御ポリシーと呼ばれます（制御ポリシー）。 管理ポリシーは、エージェントの状態に基づいて、エージェントが次に実行するアクションを決定する一連のルールです。



カブトムシアルゴリズムでは、Mラインはエージェントが次にどこにいるべきかを明確に示します。 エージェントの現在の位置からターゲットまでの線ではなく、M線に従うことを選択したのはなぜですか？ 答えは、M-lineは単なるヒューリスティックであるということです。 ヒューリスティックは、アルゴリズムの次のステップを報告するために使用される一般的なルールです。 このルールにより、アルゴリズムに関する人間の知識が得られます。 ヒューリスティックの選択は、多くの場合、このようなアルゴリズムを開発する上で重要な部分です。 間違ったヒューリスティックを選択すると、アルゴリズムが完全に機能しなくなる可能性があります。



信じられないかもしれませんが（最初は信じていませんでした）、カブトムシアルゴリズムは、最初からゴールまで移動する2次元の円の分野で解決されるすべての問題を解決します。 これは、エージェントまたはターゲットの場所に関係なく、エージェントが目標を達成できる場合、ビートルアルゴリズムがこれを可能にすることを意味します。 これの証明はこの記事の範囲外ですが、必要に応じて読むことができます。 アルゴリズムがその分野のすべての問題を解決できる場合、そのアルゴリズムは完全アルゴリズムと呼ばれます 。



しかし、ビートルアルゴリズムはこのタイプのすべての問題を解決できるという事実にもかかわらず、それによって作成される軌道は、エージェントが目標を達成できる最良のカテゴリとは限りません。 実際、ビートルアルゴリズムにより、エージェントはかなり愚かなことをすることがあります（時計回り方向に小さく、反対方向に巨大な障害物を作成しようとするだけで、あなたは私が意味することを理解します。時間」の場合、カブトムシアルゴリズムは決して最適ではありません。

最適な計画：可視性グラフ

そして、最適な（最短）経路に沿った障害物間の円の動きの問題を解決する必要がある場合はどうなりますか？ これを行うには、ジオメトリを使用して、この問題を解決するための最適なアルゴリズムを決定します。 まず、次のことに注意してください。

• 2次元ユークリッド平面では、2点間の最短経路は直線です。
• 直線パスのシーケンスの長さは、各ラインの長さの合計です。
• 多角形は直線（またはエッジ）で構成されているため、 凸多角形を完全にバイパスする最短パスには、多角形のすべてのエッジが含まれます。
• 非凸多角形を迂回するために、最短パスには多角形の凸包のすべてのエッジが含まれます。
• ポリゴンの端に正確に位置する点がこのポリゴンに接触します

「凸」、「非凸」、「凸包」の定義を理解することは、この記事を理解する上でそれほど重要ではありませんが、これらの定義は最適な軌道計画を作成するのに十分です。 次のことを想定してみましょう。

• 私たちのエージェントは、無限に小さなサイズの2次元の点です 。
• 世界のすべての障害を閉じたポリゴンに減らすことができます 。
• エージェントは任意の方向に直線で移動できます。

次に、エージェントが目標を達成するための最適なプランを見つけ、世界の可視性のグラフと呼ばれるものを作成します。 ジオメトリに加えて、グラフについても少し学ぶ必要があります。 グラフ理論はこの記事のトピックではありませんが、本質的にグラフはエッジと呼ばれる抽象的なオブジェクトによって他のノードに接続された抽象的なオブジェクト（ ノードと呼ばれる ）のグループにすぎません。 グラフの力を使用して、エージェントが住んでいる世界を記述することができます。 ノードは、何も触れずにエージェントを配置できる場所と言えます。 エッジとは、エージェントが移動できるノード間のパスです。



これを前提として、次のように可視性グラフプランナーを定義できます。



: VISIBILITY GRAPH PLANNER

• G.
  
  
  
  
• G.
  
  
  
  
• G.
  
  
  
  
• .
  
  
  
  
• G .
  
  
  
  
• V :
  
  
  
  
  
  
  • V . , G.
    
    
    
    
  • V. , G.
    
    
    
    
  • (, A*) , .
    
    
    
    

可視性グラフは次のとおりです：（破線）









そして、最終的なパスは次のようになります。









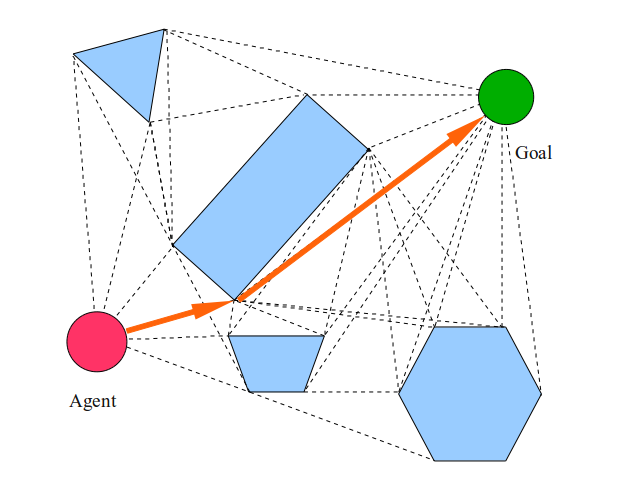
エージェントは任意の場所から他の場所へ直線的に移動できる極小点であるという仮定により、コーナー、顔、および自由空間を正確に通過する軌道があり、エージェントが移動しなければならない距離を最小限に抑えます目標。



しかし、エージェントがポイントでない場合はどうでしょうか？ オレンジのパスが台形と長方形の間のエージェントをどのように導くかに注目してください。 明らかに、エージェントはこのスペースを絞ることができないため、この問題を何らかの方法で解決する必要があります。



1つの解決策は、エージェントがポイントではなく、ディスクであると想定することです。 この場合、エージェントの半径に対するすべての障害を単純に膨らませて、エージェントがこの肥大化した世界のポイントであるかのように計画できます。









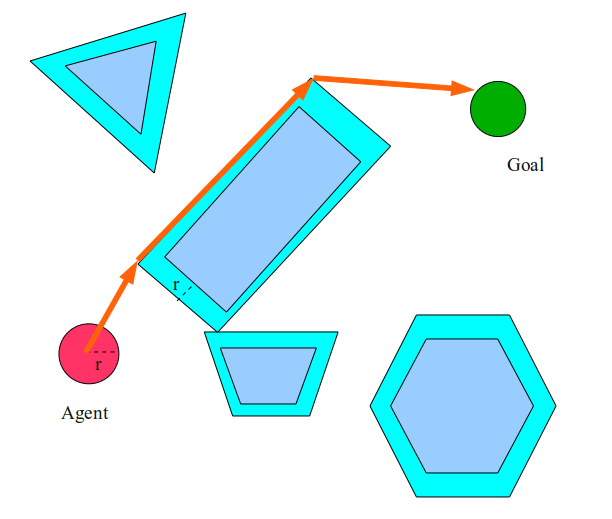
この場合、エージェントは台形と長方形の間のスペースに収まらないため、長方形の右側ではなく左側へのパスを選択します。 この「膨張」操作は実際には非常に重要です。 本質的に、エージェントがポイントであるという仮定が真実のままであるように、世界を変えました 。



この操作は、世界の構成空間の計算と呼ばれます 。 構成スペース（またはCスペース）は、エージェントの構成が単一のポイントで表される座標系です。 ワークスペース内の障害物は、エージェントを条件付き構成にし、エージェントの衝突をチェックすることにより、構成スペース内の障害物に変換されます。 この構成でエージェントが作業スペース内の障害物に触れると、エージェントは構成スペース内の障害物になります。 非円形のエージェントがある場合、障害物を膨らませるために、いわゆる和を使用します

ミンコフスキー



2次元空間の場合、これは退屈に見えるかもしれませんが、これはまさに障害物を「膨張させる」ために行っていることです。 新しい「肥大化」スペースは、実際には構成スペースです。 より多次元の空間では、事態はさらに複雑になります！



可視性グラフプランナーは素晴らしいものです。 最適かつ完全であり、 ヒューリスティックに依存しません。 可視性グラフプランナーのもう1つの大きな利点は、適度なマルチクエリ機能です。 マルチクエリスケジューラは、新しい目標を処理するときに古い計算を再利用できます。 可視性グラフの場合、ターゲットまたはエージェントの場所を変更するとき、エージェントとターゲットからグラフのエッジを再構築するだけです。 これらの利点により、このようなスケジューラはゲームプログラマにとって非常に魅力的です。



実際、現代のゲームの多くは、計画に可視性グラフを使用しています。 可視性グラフの原則の一般的なバリエーションは、 Nav（igation）Meshです。 Nav Meshでは、可視性のグラフが基礎として使用されることがあります（他のヒューリスティックと共に、敵、オブジェクトなどまでの距離）。 Nav Meshは、デザイナーまたはプログラマーによって変更される場合があります。 各Nav Meshはファイルとして保存され、個々のレベルで使用されます。



Overlordビデオゲームで使用されるNav Meshのスクリーンショットは次のとおりです。









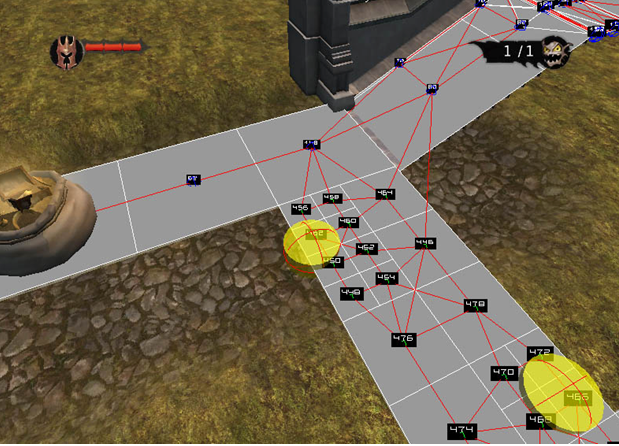
すべての利点にもかかわらず、可視性グラフの方法には重大な欠点があります。 たとえば、可視性グラフの計算は非常にコストのかかる操作になる可能性があります。 障害物の数が増えると、可視性グラフのサイズが著しく大きくなります。 可視性グラフの計算コストは​​、頂点の数の2乗として増加します。 さらに、最適性を維持するために障害物を変更した場合、可視性グラフの完全な再計算が必要になる可能性があります。



ゲームプログラマーは、ヒューリスティックを使用してグラフの作成を高速化し、エッジを介して結合しようとするノードを選択するためのあらゆる種類のトリックを発明しました。 また、ゲーム設計者は、グラフ可視性アルゴリズムのヒントを提供して、最初に接続するノードを決定できます。 これらすべてのトリックは、可視性のグラフが最適でなくなり、プログラマの単調な作業が必要になる場合があるという事実につながります。



ただし、可視性グラフで最も深刻な問題は（私の意見では）、一般化されていないことです。 彼らは1つの問題を解決し（ポリゴンの障害物がある2D平面で計画する）、それを非常にうまく解決します。 しかし、2次元平面上にない場合はどうでしょうか？ エージェントを円で表すことができない場合はどうなりますか？ 障害物がどうなるかわからない場合、またはポリゴンの形で表現できない場合はどうなりますか？ そして、可視性グラフを使用して、トリックなしで問題を解決することはできません。



幸いなことに、これらの問題のいくつかを解決する「実行して忘れる」原理に近い他の方法があります。

格子で検索：A *とそのバリエーション

可視性グラフは、抽象的なグラフの最適化検索品質とユークリッドジオメトリの基本的なルールを使用するため機能します。 ユークリッド幾何学は、検索に対して「基本的に正しい」グラフを提供します。 そして、抽象検索自体が最適化に関与しています。



しかし、ユークリッド幾何を完全に放棄し、抽象的なグラフを検索することで問題全体を単純に解決したらどうでしょうか？ したがって、ジオメトリに直面してメディエーターを排除し、さまざまなタイプの問題を解決できます。



問題は、多くの異なるアプローチを使用してタスクをグラフ検索エリアに転送できることです。 ノードは何になりますか？ リブとは正確には何ですか？ あるノードを別のノードに接続するとはどういう意味ですか？ アルゴリズムのパフォーマンスは、これらの質問にどのように答えるかに大きく依存します。



グラフ検索アルゴリズムが「最適な」答えを与えたとしても、それ自体の内部構造に関してのみ「最適」です。 これは、グラフ検索アルゴリズムによる「最適な」答えが必要な答えであることを意味するものではありません。



これを前提として、最も一般的な方法でグラフを定義しましょう： グリッドとして。 仕組みは次のとおりです。



: DISCRETIZE SPACE

• , .
  
  
  
  
• , .
  
  
  
  
• , , .
  
  
  
  
• , , , .
  
  
  
  
• .
  
  
  
  
• .
  
  
  
  

「隣接」も注意すべきもう1つの側面です。 ほとんどの場合、「 現在のセルと少なくとも1つの共通の角度を持つセル 」（これは「ユークリッド隣接」と呼ばれます）または「 現在のセルと少なくとも1つの共通の面を持つセル 」（これは「マンハッタン隣接」と呼ばれます） ） グラフ検索アルゴリズムによって返される答えは、隣接定義の選択に大きく依存します。



ケーススタディでのサンプリングステージは次のとおりです。









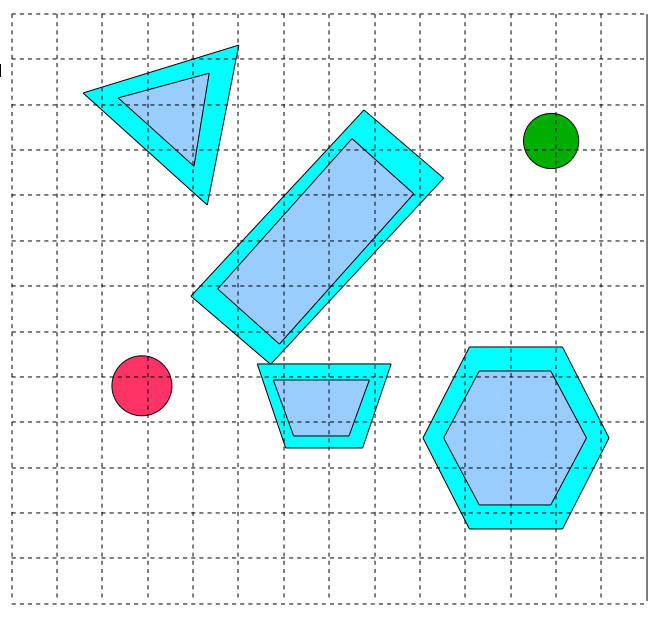
ユークリッド隣接メトリックに従ってこのグラフを検索すると、次のような結果が得られます。









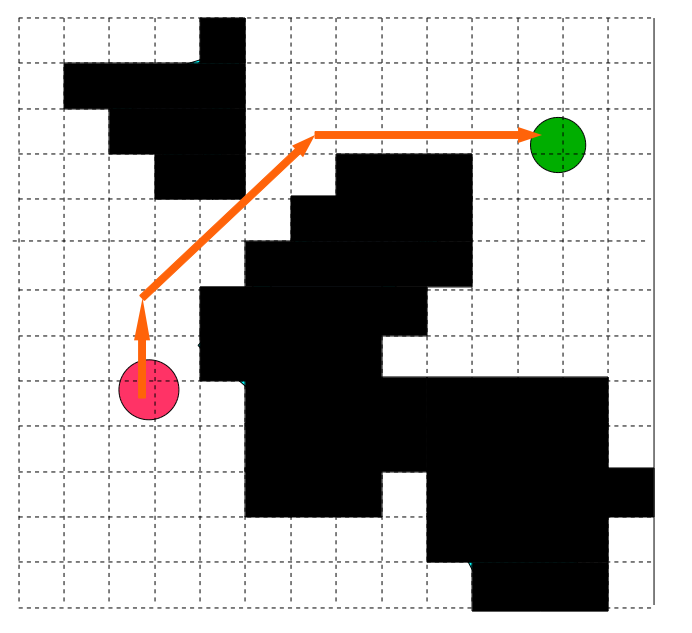
ラティス検索問題を解決するために使用できる他の多くのグラフ検索アルゴリズムがありますが、最も一般的なのはA *です。 *は、開始ノードから開始して、ヒューリスティックを使用してノードで検索を実行するダイクストラのアルゴリズムに似ています。 A *は他の多くの記事やチュートリアルでよく研究されているため、ここでは説明しません。



A *およびその他のグリッドグラフ検索方法は、ゲームで最も一般的なスケジューリングアルゴリズムの一部であり、離散化グリッドは、A *を構成する最も一般的な方法の1つです。 多くのゲームでは、タイルやボクセルを使用して世界を表現しているため、多くのゲームではこの検索方法が理想的です。



離散格子（A *を含む）上のグラフの検索方法は、内部構造に応じて最適です。 また、 完全な解像度です。 これは完全性の弱い形式であり、ラティスの細かさが無限になる傾向がある場合（つまり、セルのサイズが無限に小さくなる傾向がある場合）、アルゴリズムは解決すべき問題をますます解決します。



特定の例では、グリッド検索方法はマルチクエリではなくシングルクエリです。これは、通常、グラフ検索では新しいターゲットに一般化して構成を開始するときに古い情報を再利用できないためです。 ただし、サンプリング手順はもちろん再利用できます。



グラフベースのメソッドのもう1つの重要な利点（私の意見では、主なもの）は、完全に抽象的であることです。これは、追加のコスト（安全性、滑らかさ、必要なオブジェクトの近接性など）を考慮して、自動的に自動化できることを意味します。さらに、まったく異なる問題を解決するために、同じ抽象コードを使用できます。DwarfCorpゲームでは、モーションプランニングとシンボリックアクションプランニングの両方に同じA *スケジューラーを使用します（エージェントが抽象グラフとして実行できるアクションを表すために使用）。



ただし、グリッド検索には少なくとも1つの重大な欠陥があります。非常に多くのメモリを消費します。すべてのノードが最初から単純な方法で構築されている場合、世界のサイズが大きくなると、メモリが非常に早く使い果たされます。問題の大部分は、グリッドに大量の空きスペースを保存する必要があるという事実にあります。この問題を最小限に抑えるために、最適化手法が存在しますが、基本的には、世界のサイズと問題の次元数の増加に伴い、ラティスのメモリ量が大幅に増加します。したがって、この方法は、より多くの複雑なタスクには適用できません。



この方法の別の重大な欠点は、グラフ検索自体にかなり時間がかかることです。世界で数千のエージェントが同時に移動する場合、または多くの障害物が位置を変更する場合、ラティスサーチは適用できない場合があります。私たちのゲームDwarfCorpでは、計画にいくつかのスレッドが与えられています。大量のプロセッサ時間を消費します。あなたの場合、これも可能です！

管理ポリシー：潜在的な機能とフローフィールド

交通計画の問題を解決する別の方法は、軌道計画のカテゴリーでそれについて考えるのを止めて、管理政策のカテゴリーでそれを知覚し始めることです。覚えておいてください、私たちはカブトムシのアルゴリズムが軌道プランナーとして、知覚できることを言ったと経営方針として？そのセクションでは、構成を受け取り、アクション（または「制御入力」）を返す一連のルールとしてポリシーを定義しました。



カブトムシアルゴリズムは、障害物に出くわすまでターゲットに向かって移動し、障害物を時計回りにバイパスするようエージェントに指示する単純な管理ポリシーと考えることができます。エージェントは、文字通りこれらのルールに従い、目標へのパスに沿って移動できます。



管理ポリシーの主な利点は、一般に世界のローカルな知識以上の何かを持つエージェントに依存しないこと、およびコンピューティングが非常に高速であることです。数千（または数百万）のエージェントが同じ管理ポリシーを簡単に遵守できます。



バグアルゴリズムよりも優れた管理ポリシーを考え出すことはできますか？それらの1つ、非常に有用な「潜在的なフィールドポリシー」を検討する価値があります。彼女は、ターゲットに引き付けられ、障害物によってはじかれた荷電粒子の形でエージェントのシミュレーションを実行します。



: POTENTIAL FIELD POLICY

• a b
  
  
  
  
• g.
  
  
  
  
• o.
  
  
  
  
• o r.
  
  
  
  
• u = a * g^ + B * r^, v^ v.
  
  
  
  
• .
  
  
  
  

このポリシーを理解するには、線形代数の知識が必要です。本質的に、制御入力信号は、引力項と反発項の2つの項の加重和です。各メンバーの重みの選択は、エージェントの最終的な軌道に大きく影響します。









潜在的なフィールドポリシーを使用して、エージェントを非常に現実的かつスムーズに移動させることができます。また、簡単に条件を追加することもできます（目的のオブジェクトへの近接または敵までの距離）。



潜在的なフィールドポリシーは並列コンピューティングで非常に迅速に計算されるため、この方法で何千ものエージェントを非常に効果的に制御できます。この管理ポリシーは事前に計算され、各レベルのグリッドに保存された後、デザイナーが必要に応じて変更できる場合があります（通常はフローフィールドと呼ばれます）。



一部のゲーム（特に戦略ゲーム）では、この方法が非常に効率的に使用されます。戦略ゲームで使用されるフローフィールドの例を次に示します最高司令官2、ユニットが自然にお互いを避け、建設を維持するように：









もちろん、フローフィールドとポテンシャルフィールドの機能には重大な欠点があります。まず、それらは決して最適ではありません。エージェントは、ターゲットに到達するのにかかる時間に関係なく、フローフィールドによって配信されます。第二に（そして、私の意見では、これが最も重要です）、それらは決して完全ではありません。エージェントがターゲットに到達する前に制御入力がリセットされた場合はどうなりますか？この場合、エージェントが「ローカルミニマム」に達したと言います。このようなケースはまれにしかないと思うかもしれませんが、実際には非常に簡単に構築できます。エージェントの前に大きなU字型の障害物を置くだけです。



最後に、フローフィールドやその他の管理ポリシーの構成は非常に困難です。各メンバーの重みをどのように選択しますか？最終的には、良い結果を得るために手動で調整する必要があります。



通常、設計者は局所的な最小値を回避するためにフローフィールドを手動で調整する必要があります。このような問題は、フローフィールドの一般的なケースで考えられるユーティリティを制限します。ただし、多くの場合、これらは便利です。

構成スペースと次元の呪い

そこで、ビデオゲームで最も一般的な3つのモーションプランニングアルゴリズム、グリッド、可視性グラフ、フローフィールドについて説明しました。これらのアルゴリズムは非常に便利で、実装が簡単で、かなりよく理解されています。それらは、平面のすべての方向に移動する丸いエージェントでの2次元問題の場合に理想的に機能します。幸いなことに、ビデオゲームのほとんどすべてのタスクはこのケースに属しており、残りはデザイナーの巧妙なトリックとハードワークによって模倣できます。それらがゲーム業界で非常に積極的に使用されていることは驚くことではありません。



しかし、ここ数十年で交通計画の研究者は何をしていたのでしょうか？みんなに。エージェントが円ではない場合はどうなりますか？飛行機上にない場合はどうなりますか？彼がどんな方向にも動くことができたら？目標や障害が常に変化している場合はどうなりますか？これらの質問に答えることはそれほど簡単ではありません。



非常に単純なケースから始めましょう。これは、すでに説明した方法を使用して解決するのは非常に簡単であるように見えますが、根本的に変更せずにこれらの方法で解決することは実際に不可能です。



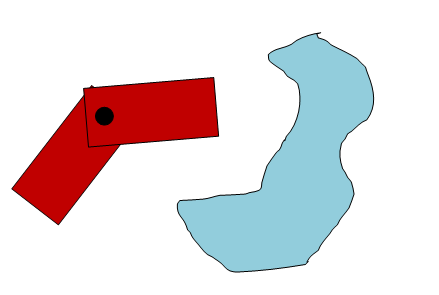
エージェントが円ではなく長方形の場合はどうなりますか？エージェントのローテーションが重要な場合はどうなりますか？私が説明している写真は次のようになります。









上記の場合、エージェント（赤）は、あらゆる方向に移動できるショッピングカートのようなものです。エージェントを移動して、ターゲットの上に正確に配置し、正しい方向に向けるようにします。



ここではおそらくカブトムシアルゴリズムを使用できますが、障害物に遭遇しないようにエージェントのターンを慎重に処理する必要があります。私たちはすぐにルールの混inに巻き込まれますが、それはラウンドエージェントの場合ほどエレガントではありません。



しかし、可視性グラフを使用しようとするとどうなりますか？これには、エージェントがポイントである必要があります。どのようにトリックを行い、ラウンドエージェントのオブジェクトを膨らませたか覚えていますか？おそらくこの場合、同様のことを行うことができます。しかし、オブジェクトをどれだけ膨張させる必要がありますか？



単純な解決策は、「最悪のシナリオ」を選択し、この計算で計画を計算することです。この場合、単にエージェントを取り、それを説明する円を決定し、このサイズの等しい円にエージェントを連れて行きます。次に、障害物を希望のサイズに膨らませます。









それは機能しますが、私たちは膨満感を犠牲にしなければなりません。解決できない多くのタスクがあります。たとえば、長くて細いエージェントが「鍵穴」を通り抜けて目標を達成する必要があるタスクを考えてみましょう。









このシナリオでは、エージェントは、ウェルに入って90度回転し、次のウェルに到達して90度回転し、そこから離れることでターゲットに到達できます。記述円によるエージェントの控えめな近似では、この問題を解決することは不可能です。



問題は、エージェント構成スペースを適切に考慮しなかったことです。ここまでは、2D障害物に囲まれた2D計画についてのみ説明してきました。このような場合、構成空間は2次元の障害物から別の2次元平面に十分に変換され、障害物を「膨張させる」効果が観察されます。



しかし実際には、ここで次のことが起こります。計画タスクに別の次元を追加しました。エージェントには、xとyの位置だけでなく、ターンもあります。私たちのタスクは、実際には3次元計画のタスクです。ワークスペースと構成スペースの間の変換は、今でははるかに複雑になっています。



このように取ることができます：エージェントが特定のターン（「シータ」を指定する）を完了したと想像してください。次に、指定された回転でエージェントをワークスペースの各ポイントに移動します。エージェントが障害物に触れた場合、このポイントは設定スペースでの衝突と見なされます。障害物ポリゴンのこのような操作は、ミンコフスキー和を使用して実装することもできます。









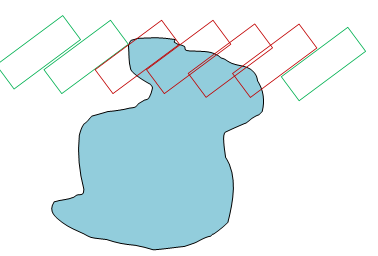
上の図では、1人のエージェントが障害物を通過しています。エージェントの赤い輪郭は衝突している構成を示し、緑色の輪郭は衝突していない構成を示します。これは当然、障害の別の「膨張」につながります。エージェントのすべての可能な位置（x、y）に対して実行する場合、構成スペースの2次元スライスを作成します。



ここで、シータを一定量だけ増やして操作を繰り返し、別の2次元スライスを取得します。









グラフ用紙を折りたたむように、スライスを重ねてx座標とy座標を揃えることができます。









叔母を限りなく薄く切ると、その結果、エージェントの3次元の構成空間が得られます。これは連続的な立方体であり、シータは下から上へと回転します。障害物は奇妙な円柱形に変わります。エージェントと彼の目標は、この新しい奇妙な空間の単なるポイントになります。









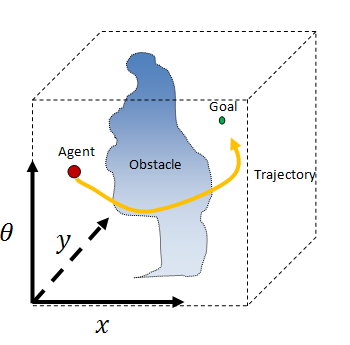
頭に入れるのはかなり難しいですが、ある意味では、このアプローチは美しくエレガントです。各次元が単純にx座標とy座標のエージェントの位置である2次元の障害物を想像できる場合、3次元の障害物も想像できます。3番目の次元はエージェントの回転です。



エージェントに別の自由度を追加したい場合はどうしますか？長さを増減したいとしますか？または、彼は考慮される必要がある腕と脚を持っていますか？そのような場合、同じことを行います-構成スペースに測定値を追加するだけです。この段階では、視覚化することは完全に不可能になり、それらを理解するには、「超平面」、「制約付き多様体」、「ハイパーボール」などの概念を使用する必要があります。









4次元の計画問題の例。エージェントは、それらを接続する軸を持つ2つのセグメントで構成されます。



エージェントが3D空間の単なるポイントになったので、従来のアルゴリズムを使用して、運動計画の問題の解決策を見つけることができます。必要に応じて、新しい3D空間にボクセルのグリッドを作成し、A *を使用できます。考えてみると、構成空間の表現を多角形メッシュとして見つけ、3Dの可視性グラフを使用することもできます。



同様に、他のディメンションについては、次のことができます。

1. エージェントと障害物の構成スペースを計算します。
2. このスペースでA *またはNav Meshを実行します。

残念ながら、これらの操作には2つの大きな問題があります。

1. N- NP- .
2. N- NP- .

コンピュータサイエンスの専門用語である「NP-complex」は、タスクが増加するにつれて指数関数的に複雑になり、他の多くの理論的困難を伴うことを意味します。



実際には、これは、計画タスクに測定値を追加し始めると、すぐに計算能力またはメモリ、あるいはその両方を使い果たすことを意味します。この問題は、次元の呪いとして知られています。 3次元では、A *で対応できますが、4、5、または6次元に達するとすぐに、A *はすぐに役に立たなくなります（Maxim Likhachevによる最近の研究にもかかわらず、十分な作業を保証できました）。



6次元計画問題の最も単純な例は、「ピアノを動かすタスク。「言い回し：立体オブジェクト（ピアノなど）を3D空間でポイントAからポイントBに移動する方法。どの方向にも移動および回転できる場合は？









OMPL からピアノを移動するタスクの例



驚くべきことに、その単純さにもかかわらず、このタスクは何十年も未解決のままです。



このため、ゲームは基本的に単純な2次元の問題に準拠し、他のすべてをシミュレートします（ピアノを動かすような解決策がある場合でも、3次元ゲームのAIの基本的な部分のようです）。



未解決の問題



70年代および80年代、モーションプランニングの研究は、構成スペースを計算する高速な方法といくつかのプランニングタスクの次元を削減するための優れた圧縮ヒューリスティックに重点を置いていました。残念ながら、これらの研究は、多数の次元の問題に対する単純で一般的な解決策の作成にはつながりませんでした。状況は、ロボット工学の研究者が一般的な多次元問題の解決の進展を動かし始めなかった90年代とゼロの始まりまで変わりませんでした。



今日、多次元空間での計画は、はるかによく研究されています。これはすべて、ランダムスケジューラと高速トラックオプティマイザーという 2つの主な発見のおかげで起こりました。それらについては、次のセクションで説明します。

ルートを見つけることと交通を計画することの違い

この記事のドラフトを公開した後、一部の読者は私の用語に混乱していることに気付きました。ゲーム開発に関する文献では、ポイントAからポイントBに移動するアクションは通常「道を見つける」と呼ばれ、私はそれを「移動を計画する」と呼びました。本質的に、モーションプランニングは、より大きな次元のスペース（たとえば、ターンやヒンジ）を考慮した「ポイント」と「パス」のより緩やかな定義によるパス検索の一般化です。



モーションプランニングは、エージェントの設定スペースでパスを検索することとして理解できます。

ランダム計画：確率的ロードマップ（PRM）

多次元計画問題に対する最初の一般的な解決策の1つは、確率的ロードマップと呼ばれます。ナビゲーションメッシュと可視性グラフのアイデアを借用し、ランダム性という別のコンポーネントを追加します。



最初に、いくつかの背景情報を紹介します。多次元空間での計画の最も複雑な側面は、構成空間を計算してから、この空間を通る最適なパスを見つけることであることを既に知っています。



PRMは、構成空間を計算するという考えを完全に拒否し、最適性の原理を忘れることにより、これらの問題の両方を解決します。このアプローチでは、距離ヒューリスティックを使用して空間の可視性のグラフがランダムに作成され、この可視性のグラフでソリューションが検索されます。また、エージェント構成の衝突チェックを比較的簡単に実行できると仮定することもできます。



アルゴリズム全体は次のようになります。



: PROBABALISTIC ROAD MAP (PRM)

• G
  
  
  
  
• G .
  
  
  
  
• N :
  
  
  
  
  
  
  • R. .
    
    
    
    
  • R, .
    
    
    
    
  • , R G.
    
    
    
    
  • G, d R.
    
    
    
    
  • N,
    
    
    
    
    
    
    • R N
      
      
      
      
    • , G.
      
      
      
      
    • A* .
      
      
      
      
    
    
    
  
  
  

要するに、各段階でランダムポイントを作成し、グラフのどのノードが「見える」か、つまり、新しいノードとグラフ内の隣接ノードの間に直線を引くことができるかどうかに基づいて、グラフ内の隣接ノードと接続します。 。



これは可視性グラフアルゴリズムに非常に似ていることがすぐにわかります。ただし、「すべての障害物」または「各頂点」については言及しません。もちろん、このような計算はNP完全です。



代わりに、PRMは、それによって作成されたランダムグラフの構造と隣接ノード間の衝突のみを考慮します。



PRMの特性



アルゴリズムはもはや最適ではなく、完全ではないことをすでに述べました。しかし、そのパフォーマンスについては何を言えますか？



PRMアルゴリズムは、いわゆる「 ". , N , PRM , . ( ), PRM . , , .



PRM . PRM ( N ) , PRM .



ご想像のとおり、そのランダム性により、PRMは非常にく、長く危険なパスを作成する可能性があります。この点で、PRMは決して最適ではありません。



基本的に、Nav Meshの可視性グラフと同様に、PRMはマルチクエリスケジューラです。これにより、エージェントは複数のスケジューリングリクエストに対してランダムグラフを効率的に再利用できます。レベル設計者は、レベルごとに1つのPRMを焼くこともできます。

なぜ事故ですか？

PRM（およびその他のランダム化アルゴリズム）の最も重要なトリックは、明示的にではなく、統計的に構成スペースを表すことです。これにより、スピードのためにソリューションの最適性を犠牲にして、それらが存在する場合に「かなり良い」決定を下すことができます。これは、プログラマーがソリューションを返す前にスケジューラーが完了する必要がある作業量を決定できるため、非常に強力なツールです。このプロパティは、リアルタイム実行アルゴリズムプロパティと呼ばれます。



本質的に、PRMの複雑さは、構成スペースの次元数の増加ではなく、サンプル数と距離パラメーターdの増加とともに増加します。これを、問題の次元が大きくなるにつれて指数関数的に時間がかかるA *または可視性グラフと比較してください。



この機能により、PRMは数百のディメンションで迅速に計画できます。



PRMの発明以来、その効率、舗装されたパスの品質、および使いやすさを向上させるアルゴリズムのさまざまなバリエーションが提案されてきました。

ランダム化されたツリーのランダム化探索（RRT）

PRMマルチタスクが不要な場合があります。多くの場合、以前の計画要求について何も知らずに、ポイントAからポイントBに移動することをお勧めします。たとえば、スケジューリングリクエスト間の環境が変更された場合、以前のスケジューリングリクエストから保存された情報を再作成するよりも、単にゼロから再スケジュールする方が良い場合があります。



そのような場合、ポイントAからポイントBへの移動を一度だけ計画したいという事実を考慮して、ランダムグラフを作成する考え方を変更できます。これを実装する1つの方法は、グラフをツリーに置き換えることです。



ツリーは、ノードが「親」と「子」に配置された特別なタイプのグラフであるため、ツリー内の各ノードには、親ノードが1つと0個以上の子があります。



移動計画をツリーとしてどのように表現できるかを見てみましょう。構成空間を体系的に調査するエージェントを想像してください。



エージェントが何らかの状態にある場合、現在の状態（または、この場合は無限の状態）から移行できる状態が他にもいくつかあります。これらの状態のそれぞれから、彼は他の状態に行くことができます（しかし、彼はすでに彼が来た状態にいたので、戻りません）。



エージェントが存在する状態を「親」ノードとして保存し、エージェントがそこから移動するすべての状態を「子」ノードとして保存する場合、エージェントの現在の状態からすべての場所に成長するツリーのような構造を形成できます。エージェントを潜在的に見つけることができます。遅かれ早かれ、エージェントツリーはそれをターゲットの状態に導き、解決策を見つけます。



このアイデアは、状態を体系的に拡張し、それらをツリーのような構造に追加するA *アルゴリズムに非常に似ています（技術的な観点から、有向非循環グラフに）。ターゲットの構成を達成するために、エージェントの初期構成からツリー



をランダムに成長させることはできますか？



2つのクラスのアルゴリズムがこの問題を解決しようとします。どちらも90年代後半とゼロ初期に発明されました。 1つのアプローチは「中心」です-ツリー内のランダムノードを選択し、ランダムな方向に成長します。このクラスのアルゴリズムは「EST」、つまり「拡張スペースツリー」（「拡張可能な空間ツリー」）と呼ばれます。 2番目のアプローチは「サンプル指向」です。これは、空間内のノードのランダムな選択から始まり、このランダムなサンプルの方向に最も近いノードを成長させます。このタイプのアルゴリズムは、「RRT」（「ランダム化されたツリーの迅速な探索」、「ランダム化されたツリーのランダムな調査」）と呼ばれます。



一般に、RRTはESTよりもはるかに優れていますが、理由の説明はこの記事の範囲外です。



RRTの仕組みは次のとおりです。



: RAPIDLY EXPLORING RANDOMIZED TREE (RRT)

• T.
  
  
  
  
• T .
  
  
  
  
• N ,
  
  
  
  
  
  
  • R.
    
    
    
    
  • T R . K.
    
    
    
    
  • K R , :
    
    
    
    
    
    
    • .
      
      
      
      
    • T .
      
      
      
      
    • d K, .
      
      
      
      
• d , .
  
  
  
  

上の図は、実行中のアルゴリズムの1つのステップをほぼ示しています。ランダムサンプル（オレンジ、r）を取得し、それに最も近いノード（黒、k）を見つけて、ランダムサンプルの「方向のステップ」を取る1つ以上の新しいノードを追加します。



ツリーは、目標に達するまでランダムに成長し続けます。また、ターゲットをランダムに選択して、直線を描くように熱心に試みます。実際には、ターゲットがサンプルに陥る確率は、構成スペースの乱雑さに応じて、せいぜい30％から80％の範囲になります。



RRTは比較的単純です。それらはほんの数行のコードで実装できます（ツリー内で最も近いノードを簡単に見つけることができると仮定）。



RRTプロパティ



おそらく、RRTアルゴリズムが確率的に完全であることに驚かないでしょう。最適ではありません（多くの場合、過度に最適ではありません）。









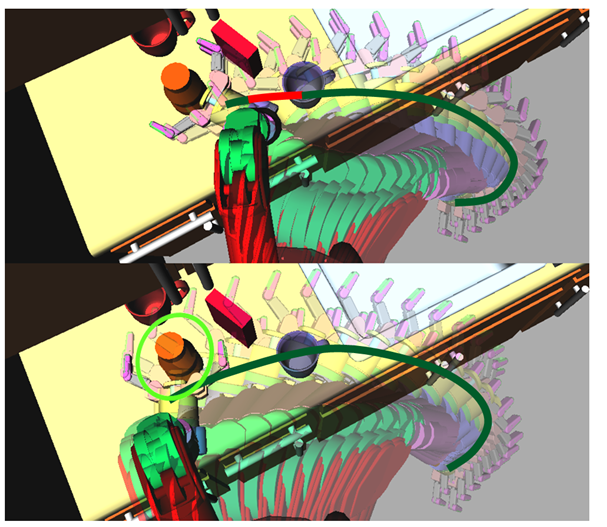
ロボットマニピュレーターは、非常に多次元のシステムと見なされます。この場合、それぞれ7つのヒンジを備えた2つのマニピュレーターがあり、単一ヒンジのワイヤーカッターを保持しています。システムは15次元です。運動計画の現代の研究は、このような多次元システムを研究しています。



また、RRTは単純であるため、通常は非常に高速です（少なくとも多次元システムの場合）。最速のRRTバリエーションを使用すると、7次元以上の多次元システムのソリューションがミリ秒単位で見つかります。測定の数が数十に達すると、RRTは通常、このような問題を解決する上で他のすべてのプランナーを上回ります。しかし、それは、研究者のコミュニティで「速い」多次元計画手段ことを検討する価値があり秒または、アクションのパイプライン全体を7つの次元で完了するか、20 分以上の次元で最大1 分間完了します。その理由は、RRTパスは多くの場合、直接使用するにはひどすぎて、長い前処理ステップを経る必要があるためです。これは、A *を使用するプログラマに衝撃を与える可能性があります。A*は、2次元の問題の解決策をミリ秒単位で返します。しかし、7次元のタスクに対してA *を実行してみてください-ソリューションが返されることはありません！



RRTのバリエーション



RRTアルゴリズムの発明とその大成功の後、他の領域に拡張したり、パフォーマンスを向上させるために多くの試みが行われました。知っておく価値のあるRRTバリエーションの一部を次に示します



。RRTConnect-最初と目標から2本の木を成長させ、ランダムな間隔で直線でそれらを接続しようとします。私の知る限り、これは測定回数が多いタスクの最速のスケジューラーです。ここに、私が作成したRRT接続実装の美しい図を示します（白-障害物、青-空き領域）：









RRT * -この10年で発明されました。ツリーのリバランスによる最適性の保証。RRTConnectよりも数千倍遅い。



T-RRT —コスト関数の勾配を調べることにより、高品質のRRTパスを作成しようとします。



制約付きRRT-任意の制限（距離、コストなどの制限など）で計画できます。RRTより遅いが、それほどではない。



キノダイナミックRRT-構成スペースではなく、入力制御信号のスペースで計画を実行します。車、カート、船、その他のエージェントが順番を自由に変えられないように計画することができます。DARPAグランドチャレンジで積極的に使用されています。キノダイナミクス以外のプランナーよりもはるかに遅いです。



離散RRTは、メッシュ用のRRTの実装です。2次元空間では速度がA *に匹敵​​し、3Dでは多次元システムでそれよりも高速です。



DARRT - 2012年に発明されました。シンボリックアクションを計画するためのRRTの実装（以前はA *の範囲と見なされていました）。

パスの切断と最適化

ランダム化されたスケジューラは最適性を保証しないため、それらが作成する軌跡は非常にひどいものになる可能性があります。したがって、ランダム化されたスケジューラによって作成されたエージェントに直接使用する代わりに、ディレクトリは多くの場合、品質を向上させる複雑な最適化の段階に移行されます。今日、このような最適化手順は、ランダム化されたプランナーのプランニング時間の大部分を占めています。わずか数ミリ秒で可能なパスを返すために7次元RRTが必要になる場合がありますが、最終パスを最適化するには最大5秒かかる場合があります。



一般的な場合、トラジェクトリオプティマイザーは、初期トラジェクトリとコスト関数を取得するアルゴリズムであり、最低トラジェ​​クトリを持つように初期トラジェクトリを変更します。たとえば、必要なコスト関数がパスの長さを最小にすることである場合、この関数のオプティマイザーは元のパスを取得し、このパスを短くするように変更します。このタイプのオプティマイザーは、トラジェクトリーショートカッターと呼ばれます。



最も一般的で非常にシンプルなパスカッター（「確率的上昇カッター」と呼ばれる確率的ヒルクライミングショートカッター）は、次のように機能します。



: Stochastic Hill Climbing Shortcutter

• N :
  
  
  
  
  • T ( t1 t2)
    
    
    
    
  • t1 t2 , .
    
    
    
    
  • , t1 t2
    
    
    
    
    
    
    • , T t1 t2,
      
      
      
      
    
    
    
  
  
  

この軌跡カッターは、「ショートパス」の概念を他のコスト関数（たとえば、障害物からの距離、滑らかさ、安全性など）に置き換えることで簡単に変換できます。時間が経つにつれて、軌道はコスト関数の「極小」と呼ばれるものに分類されます。軌道の長さ（またはコスト）は減少しなくなります。



説明した上昇よりもはるかに高速に動作する、より洗練された軌道オプティマイザーがあります。このようなオプティマイザーは、多くの場合、計画タスクの範囲に関する知識を使用して作業をスピードアップします。

計画パスの最適化

多次元モーションプランニングの問題を解決するもう1つの方法は、「空間を検索する」というアイデアから離れてパスを見つけることです。代わりに、パスの最適化に直接焦点を合わせます。



軌跡を短くしたり、他の基準を満たすように軌道を最適化できるというのが本当なら、直接最適化を使用して問題全体を解決することは可能ですか？



最適化を使用してプランニングの問題を直接解決するモーションプランナーが多数います。通常、このために、それらはパラメトリックモデルを使用して軌跡を表し、モデルのパラメーターを極小値に達するまでインテリジェントに変更します。



このプロセスを実装する1つの方法は、勾配降下法と呼ばれます。 . C(T) , T — , D_C(T) , , .



. :



: Gradient Descent Trajectory Optimizer

1. , .
   
   
   
   
2. . T_0.
   
   
   
   
3. , , , .
   
   
   
   
4. , - . , , 3.
   
   
   
   
5. 4.
   
   
   
   
6. , .
   
   
   
   

«» , . , . ( ).









画像では、ポイントの勾配が*負*コスト関数の勾配を表していることに注意してください）



実際には、計画としての軌道の最適化はかなり難しく、混乱したトピックであり、この記事では判断するのが困難です。軌道の勾配の計算は本当に何を意味しますか？ラバーテープとしての軌跡の認識とはどういう意味ですか？変分解析に関連するこれらの質問には非常に複雑な答えがあります。



経路最適化は、多次元交通計画のためのランダム化された検索プランナーの強力な代替手段であることを知るだけで十分です。それらの利点は、並外れた柔軟性、最適性の理論的保証、非常に高いパス品質および相対速度です。









Chompまで、昇給クラブ（の作品からイラストを使用したロボットドラガンら。アル）



近年では、非常に高速なオプティマイザ軌道のホストは、多次元の問題を解決するには、強力な競争相手のRRTとPRMとなっています。それらの1つであるCHOMPは、勾配降下法と距離フィールドを使用した障害物のスマートな表現を使用します。もう1つのTrajOptは、凸集合の形で障害物を提示し、逐次2次計画法を使用します。

取り上げなかった重要なトピック

私が言ったことに加えて、まだ理論的な運動計画の世界があります。他に何があるか簡単に説明します。



非ホロノミック計画



エージェントが任意の方向に任意の速度で移動できる場合のみを考慮しました。しかし、そうでない場合はどうなりますか？たとえば、車は横にスライドできませんが、前後に移動する必要があります。このような場合は、「非ホロノミック」計画タスクと呼ばれます。このタスクにはいくつかの解決策がありますが、どれも高速ではありません！現代のカープランナーの平均計画を計算するのに最大1 分かかります。



制限付き計画



非ホロノミック計画とは、「制約付き計画タスク」と呼ばれるさらに別のタスクセットを指します。移動の制限に加えて、エージェントの物理的構成、エージェントが移動に使用する最大力、またはエージェントが障害物以外の物体によって制限される領域にも制限があります。制限付きの一般化された計画には多くの解決策もありますが、高速なものはごくわずかです。



時間計画



別の次元として計画に時間を追加して、エージェントが移動するターゲットを追跡したり、移動する障害物を回避したりできるようにします。正しく実装すると、このような手法は驚くべき結果をもたらす可能性があります。ただし、エージェントはしばしば未来を予測できないため、この問題は扱いにくいままです。



ハイブリッドプランニング：



エージェントのプランが1つの軌跡で想像できない場合はどうなりますか？エージェントが途中で他のオブジェクトと対話する必要がある場合（そして、単にそれらを回避するだけではない場合）これらのタイプのタスクは、通常「ハイブリッド計画」と呼ばれます-通常、タスクの幾何学的側面に関連する抽象的な側面があります。これらのタイプのタスクについては、明確で一般的に受け入れられている決定もありません。

結論

この記事では、モーションプランニングのいくつかの基本概念を検討し、エージェントをポイントAからポイントBに、最も単純なものから非常に複雑なものに移動する問題を解決するいくつかのクラスのアルゴリズムを提示しました。



モーションプランニングの研究における最近の進歩により、これまで未解決だったさまざまな問題をパーソナルコンピューター（および場合によってはビデオゲームエンジン）で解決できるようになりました。



残念ながら、これらのアルゴリズムの多くは、特に自動車、船舶、その他すべての方向に移動できない車両では、リアルタイムで使用するには遅すぎます。これにはすべて、さらなる調査が必要です。



記事があなたにとってあまり複雑ではないように思われ、その中に何か有用なものを見つけたと思います！



以下は、この記事で説明したすべてのアルゴリズムの要約表です（ここでは、非動的な計画のみが考慮されることを考慮する必要があります）。