虹彩の模倣：シェーダーCD-ROM

このチュートリアルでは、 iridiscenceについて説明します。 このチュートリアルでは、色の反射を作成するマテリアルの動作を理解し、再現するために、光の本質を探ります。 このチュートリアルはUnityのゲーム開発者を対象としていますが、このチュートリアルで説明する手法は、UnrealやWebGLなどの他の言語で簡単に実装できます。









チュートリアルは、次のパートで構成されます。

• パート1.光の性質
• パート2.虹の改善-1
• パート3.虹の改善-2
• パート4.回折格子を理解する
• パート5.回折格子の数学
• パート6. CD-ROMシェーダー：回折格子-1
• パート7.シェーダーCD-ROM：回折格子-2

はじめに

Iridiscenceは、光の角度や視野角が変化するとオブジェクトの色が変化する光学現象です。 この効果のおかげで、泡には非常に幅広い色のパレットがあります。









虹色は、流出したガソリンのプール、CD-ROMの表面、さらには新鮮な肉にも現れます。 多くの昆虫や動物は、虹彩を使用して、適切な色素なしで花を作ります。









これは、これらすべてのオブジェクトの表面にある光と微細構造の相互作用により虹彩が発生するためです。 昆虫の外部骨格のCD-ROMトラックとフレーク（下の画像を参照）は、相互作用する光の波長と同程度の大きさを持っています。 実際、虹彩は光の真の波動性を明らかにした最初の現象でした。 私たちは、光が何であるか、どのように機能し、人間の目でどのように知覚されるかを最初に理解することなく、虹彩を説明し再現することはできません。

光の性質

多くの亜原子粒子と同様に、光は粒子と波の特性を同時に示します。 多くの場合、光は1番目または2番目としてモデル化されます。 ほとんどのアプリケーションでは、光は光子と呼ばれる数兆個の個々の粒子で構成されていると考えることができます。 たとえば、ほとんどのシェーダーは、フォトンが小さなビリヤードボールのように振る舞い、衝突した角度で​​オブジェクトから反射されると考えています（下図を参照）。









しかし、光は波としてもモデル化できます。 物理学者はこの概念に精通していますが、開発者は常にそれを認識しているわけではありません。 それでは、光が波の形で存在することの意味を理解するのに時間をかけましょう。



私たちは皆海の波を知っています。 海面上の各ポイントには高さがあります。 平均値が高いほど、波は高くなります。 水面を乱すと、波はエネルギーが消散するまで海を伝播し始めます。



光は波ですが、水面上の高さとして測定するのではなく、 電磁場が目的のポイントで持っているエネルギーとして定義されます。 このモデルによると、光は空間を伝播する電磁場の摂動です。 波を作るか、周囲の空間に多くの光子を放出する電球を想像できます。



光子によって伝達されるエネルギーの量によって、光の色が決まります。 低エネルギーの光子は赤と認識されます。 高エネルギーの光子は紫色として認識されます。 波には、粒子エネルギーに似た特性があります： 波長 。 直感的な理解のために、これは波の2つのピーク間の距離であると言えます。









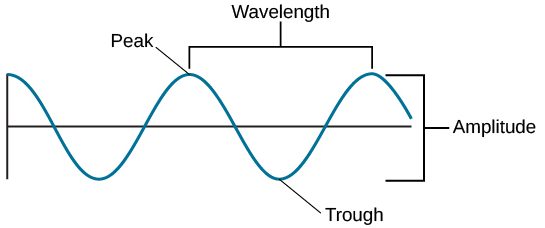
光は常に同じ速度（毎秒約299,792,458メートル）で移動します。つまり、電磁波は同じ速度で伝播します。 速度は一定ですが、波長は異なる場合があります。 高エネルギー光子は短波長です。 最終的に色を決定するのは光の波長です。









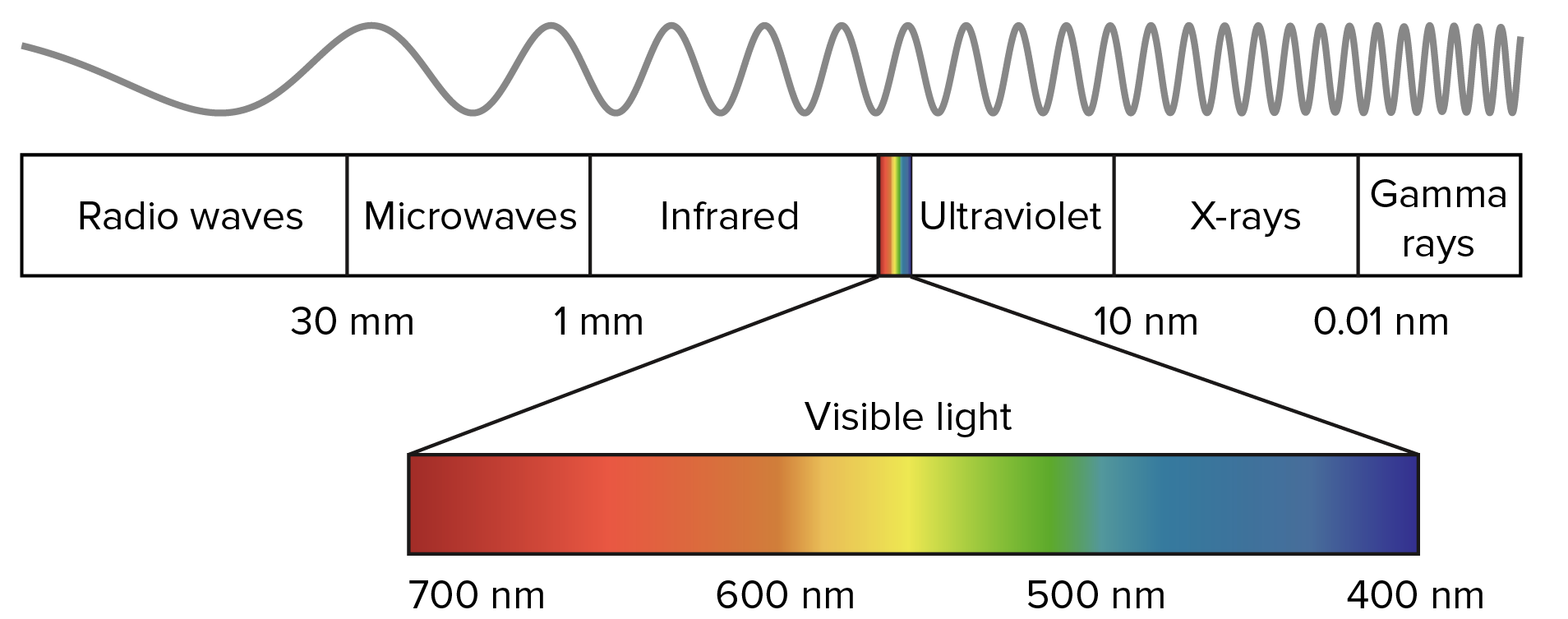
上の図でわかるように、人間の目は、約700ナノメートルから400ナノメートルの範囲の波長の光子を知覚できます。 ナノメートルはメートルの10億分の1です。

次は？

チュートリアルの残りの部分でこの簡単な紹介をした後、iridiscenceとそのUnityでの実装の理解に焦点を当てます。

• 虹の改善。 前述のように、人間の目では異なる波長の光が異なる色として認識されます。 次の2つのパートでは、これらの波長をRGBカラーに関連付ける方法を説明します。 このステップは、虹色の反射を高い精度で再現するために必要です。 これらのパートでは、物理的に正確で計算効率の高い新しいアプローチも紹介します。
• 回折格子。 このチュートリアルのパート4と5では、 回折格子を見ていきます。 これは、マテリアルに虹色の反射を表示させるエフェクトの1つの技術名です。 その「技術」にもかかわらず、この光学現象を支配する派生方程式は非常に単純です。 回折格子の数学に興味がない場合は、パート5をスキップできます。
• シェーダーCD-ROM。 このチュートリアルの中心は、CD-ROMシェーダーの実装です。 前のパートで収集した知識を使用して、Unityに回折格子を実装します。 Unity 5 Standard Surface Shaderの拡張です。 これにより、この効果は物理的に正確であり、写実的です。 少し手間をかけるだけで、回折格子に基づいて他の種類の虹色の反射に一致するように変更できます。

まとめると

このセクションから、iridiscenceチュートリアルを開始しました。 この記事の残りの部分では、泡からCD-ROM、流出したガソリンから昆虫に至るまで、さまざまな素材での無彩な反射をシミュレートして実現する方法を探ります。

パート2.虹の改善-1。

フォトリアリズムの世界への旅には、光がどのように機能するかだけでなく、色をどのように知覚するかを理解する必要があります。 虹にはいくつの色がありますか？ なぜピンクが含まれていないのですか？ ここでは、このパートで取り上げる問題の一部を紹介します。

はじめに

このパートでは、虹色を再現するためにコンピューターグラフィックスで使用される最も一般的な手法について学びます。 これは無駄な運動のように思えるかもしれませんが、実際には非常に実用的です。 虹の各色は、光の特定の波長に対応しています。 このような適合により、物理的に有効な反射をシミュレートできます。



次の「Improving the Rainbow-2」では、シェーダーに最適化され、同時に現時点で最良の結果を生み出す新しいアプローチを紹介します（以下を参照）。



このチュートリアルで説明したすべての手法のWebGLバージョンの比較は、 Shadertoyにあります。

花の知覚

網膜は、光を認識する目の部分です。 特定の波長の光を認識すると脳に信号を伝達できる錐体細胞があります。 光は電磁界内の波なので、コーンは電波を認識するのと同じ原理に従って機能します。 デファクトコーンは小さなアンテナです。 エレクトロニクスを研究したことがある場合、アンテナの長さはピックアップする波長に関係していることを知っておく必要があります。 それが人間の目には3種類の錐体が存在する理由です：短、中、長。 各タイプは、特定の波長範囲の認識に特化しています。









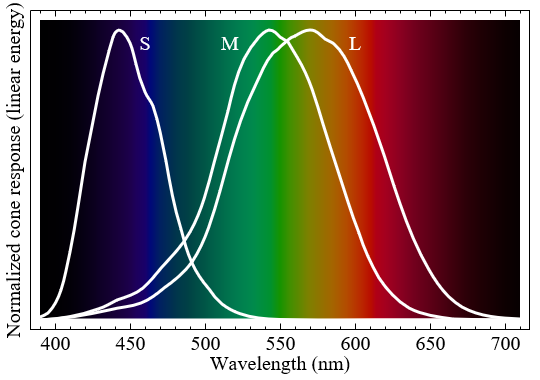
上記のグラフは、各タイプのコーンが異なる波長にどのように反応するかを示しています。 これらのタイプのコーンの1つがアクティブになると、脳はその信号を色として解釈します。 これはよく言われますが、短い、中程度、長い円錐は特定の色に対応していません。 より具体的には、各タイプは異なる色範囲に対して異なる反応を示します。



短、​​中、長の円錐が青、緑、赤を認識すると仮定するのは間違っています。 これにもかかわらず、多くの教科書（およびシェーダーも！）は、このかなり複雑な現象の比較的許容可能な近似を作成するためにこの仮定を行います。

スペクトル色

無差別を可能にする物理現象を再現したい場合は、コンピューターで色を保存および処理する方法を再考する必要があります。 Unity（または他のゲームエンジン）で光源を作成するとき、赤、緑、青の3つの主要コンポーネントの混合として色を設定できます。 赤、緑、青の組み合わせは実際にすべての可視色を作成できますが、最も基本的なレベルでは、光の働きは異なります。



光源は、一定の光子束としてモデル化できます。 異なる量のエネルギーを運ぶ光子は、私たちの目には異なる色として知覚されます。 ただし、「白色光子」は存在しません。 これは多くの光子の合計であり、それぞれが異なる波長を持ち、光に白色を与えます。



先に進むには、光自体の「ビルディングブロック」について話す必要があります。 「波長」について話すときは、虹の特定の色について考える価値があります。 このパートでは、この接続を実装するさまざまなアプローチを示します。 結果として、与えられた色に対して知覚された色を返す関数を取得したい：

fixed3 spectralColor (float wavelength);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ポストの残りでは、波長をナノメートル（10億分の1メートル）で表します。 人間の目は、400 nm〜700 nmの範囲の光を知覚できます。 この範囲外の波長は存在しますが、色として認識されません。

スペクトルマップ

下の図は、長さが400ナノメートル（青）から700ナノメートル（赤）の範囲の波を人間の目がどのように知覚するかを示しています。









可視スペクトルの色の分布が非常に非線形であることは簡単にわかります。 各波長のグラフに知覚色の対応する成分R、G、Bをプロットすると、結果として同様の結果が得られます。









この曲線を完全に説明できる単純な関数はありません。 最も単純で安価な実装アプローチは、色に波長を付加する手段としてシェーダーでこのテクスチャを使用することです。



最初に行うことは、シェーダーに新しいテクスチャへのアクセスを提供することです。 これを行うには、新しいシェーダーのProperties



ブロックにテクスチャプロパティを追加しProperties



。

 //  Properties { ... _SpectralTex("Spectral Map (RGB)",2D) = "white" {} ... } //   SubShader { ... CGPROGRAM ... sampler2D _SpectralTex; ... ENDCG ... }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

spectrumColor関数は、間隔[400,700]の波長を単に間隔[0,1]のUV座標に変換します。

 fixed3 spectral_tex (float wavelength) { //  : [400, 700] // u: [0, 1] fixed u = (wavelength -400.0) / 300.0; return tex2D(_SpectralTex, fixed2(u, 0.5)); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

特定のケースでは、波長を間隔[400、700]に強制的に制限する必要はありません。 Repeat：Clampを使用してスペクトルテクスチャをインポートすると、この範囲外のすべての値は自動的に黒になります。

JETカラースキーム

テクスチャのサンプリングは良いアイデアのように思えるかもしれません。 ただし、シェーダーの速度が大幅に低下する可能性があります。 各ピクセルが複数のテクスチャサンプルを必要とするCD-ROMの無差別性の観点から、これがどれほど重要であるかがわかります。



光スペクトルの色分布を近似する関数がいくつかあります。 おそらく最も簡単なものの1つは、JETカラースキームです。 この配色は、MATLABで既定で使用され、宇宙物理学における流体ジェットのシミュレーションの視覚化を改善するために、元は国立スーパーコンピューターアプリケーションセンターによって開発されました。









JETカラースキームは、青、緑、赤の3つの異なる曲線の組み合わせです。 これは、色を分割するときにはっきりと見られます。









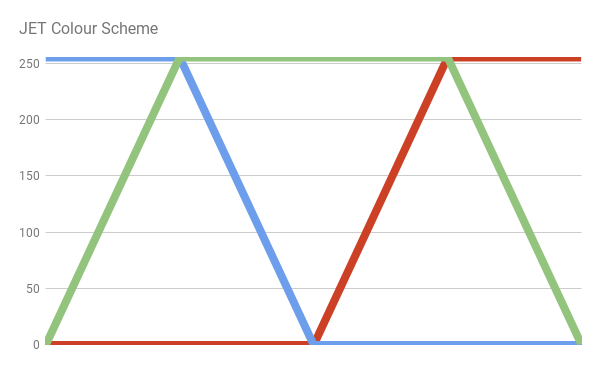
上記のスキームを構成する線の方程式を記述することにより、JETカラースキームを自分で簡単に実装できます。

 //   MATLAB Jet fixed3 spectral_jet(float w) { // w: [400, 700] // x: [0, 1] fixed x = saturate((w - 400.0)/300.0); fixed3 c; if (x < 0.25) c = fixed3(0.0, 4.0 * x, 1.0); else if (x < 0.5) c = fixed3(0.0, 1.0, 1.0 + 4.0 * (0.25 - x)); else if (x < 0.75) c = fixed3(4.0 * (x - 0.5), 1.0, 0.0); else c = fixed3(1.0, 1.0 + 4.0 * (0.75 - x), 0.0); //     [0,1] return saturate(c); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果の色のR、G、およびBの値は、Cg saturate



関数を使用して間隔[0.1]に制限されます。 カメラに対してHDR（ ハイダイナミックレンジレンダリング ）が選択されている場合、これは、1より大きいコンポーネントの色の存在を避けるために必要です。



JETカラースキームを厳密に遵守したい場合、可視範囲外の値は黒にならないことに注意してください。

ブルートンの配色

波長を可視色に変換する別のアプローチは、Dan Brutonの記事「 Visible RGB values for Visible Wavelengths 」で提案されたスキームです。 JETカラースキームで起こることと同様に、Brutonは知覚された色のおおよその分布から始まります。









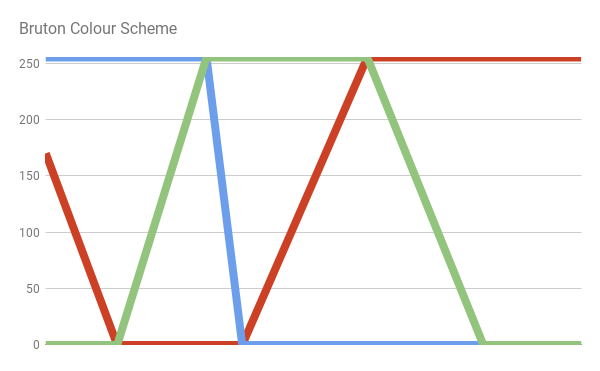
しかし、彼のアプローチは長い円錐の活動をよりよく近似しており、可視スペクトルの下部に強い紫の陰影をもたらします。









このアプローチは、次のコードに変換されます。

 //   fixed3 spectral_bruton (float w) { fixed3 c; if (w >= 380 && w < 440) c = fixed3 ( -(w - 440.) / (440. - 380.), 0.0, 1.0 ); else if (w >= 440 && w < 490) c = fixed3 ( 0.0, (w - 440.) / (490. - 440.), 1.0 ); else if (w >= 490 && w < 510) c = fixed3 ( 0.0, 1.0, -(w - 510.) / (510. - 490.) ); else if (w >= 510 && w < 580) c = fixed3 ( (w - 510.) / (580. - 510.), 1.0, 0.0 ); else if (w >= 580 && w < 645) c = fixed3 ( 1.0, -(w - 645.) / (645. - 580.), 0.0 ); else if (w >= 645 && w <= 780) c = fixed3 ( 1.0, 0.0, 0.0 ); else c = fixed3 ( 0.0, 0.0, 0.0 ); return saturate(c); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

カラースキームバンプ

JETとBrutonの配色は、不連続関数を使用します。 したがって、非常にシャープなカラーバリエーションが作成されます。 また、可視範囲外では、黒になりません。 本「GPU Gems」では、この問題は以前の配色の厳しいラインをより滑らかなバンプに置き換えることで解決されています。 各ベンドは、次の形式の規則的な放物線です。 $$$y = 1-x ^ 2$ 。 より具体的に

$$

$$bump \ left（x \ right）= \ left \ {\ begin {matrix} 0＆\ left | x \ right |> 1 \\ 1-x ^ 2＆\ mathit {otherwise} \ end {matrix} \ right 。$$

スキームの作成者であるRandima Fernandoは、次のように配置されたすべてのコンポーネントに放物線を使用します。















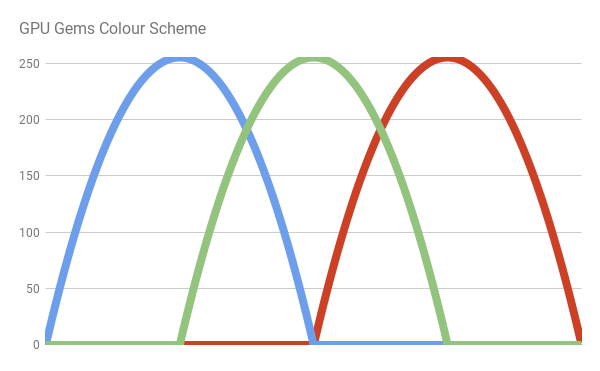
次のコードを書くことができます。

 // GPU Gems inline fixed3 bump3 (fixed3 x) { float3 y = 1 - x * x; y = max(y, 0); return y; } fixed3 spectral_gems (float w) { // w: [400, 700] // x: [0, 1] fixed x = saturate((w - 400.0)/300.0); return bump3 ( fixed3 ( 4 * (x - 0.75), // Red 4 * (x - 0.5), // Green 4 * (x - 0.25) // Blue ) ); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この配色のもう1つの利点は、テクスチャサンプルと分岐を使用しないことです。これは、品質よりも速度を優先する場合に最適なソリューションの1つになります。 このチュートリアルの最後に、この配色の改訂版を示します。これにより、高解像度の色を維持しながら、より高速になります。

スペクターの配色

最も正確な配色の1つは、ユーザーStack Overflow Spektreによって作成されたものです。 彼は、 可視スペクトルポストのRGB値で彼の方法論を説明し、太陽スペクトルから材料データの青、緑、赤の成分をサンプリングします。 その後、単純な関数で個々の間隔を埋めます。 結果を次の図に示します。









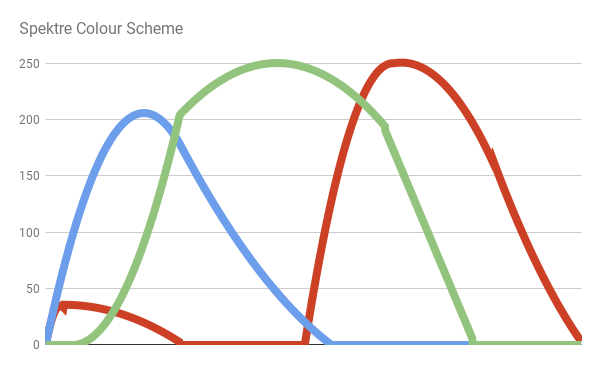
提供するもの：









そして、ここにコードがあります：

 // Spektre fixed3 spectral_spektre (float l) { float r=0.0,g=0.0,b=0.0; if ((l>=400.0)&&(l<410.0)) { float t=(l-400.0)/(410.0-400.0); r= +(0.33*t)-(0.20*t*t); } else if ((l>=410.0)&&(l<475.0)) { float t=(l-410.0)/(475.0-410.0); r=0.14 -(0.13*t*t); } else if ((l>=545.0)&&(l<595.0)) { float t=(l-545.0)/(595.0-545.0); r= +(1.98*t)-( t*t); } else if ((l>=595.0)&&(l<650.0)) { float t=(l-595.0)/(650.0-595.0); r=0.98+(0.06*t)-(0.40*t*t); } else if ((l>=650.0)&&(l<700.0)) { float t=(l-650.0)/(700.0-650.0); r=0.65-(0.84*t)+(0.20*t*t); } if ((l>=415.0)&&(l<475.0)) { float t=(l-415.0)/(475.0-415.0); g= +(0.80*t*t); } else if ((l>=475.0)&&(l<590.0)) { float t=(l-475.0)/(590.0-475.0); g=0.8 +(0.76*t)-(0.80*t*t); } else if ((l>=585.0)&&(l<639.0)) { float t=(l-585.0)/(639.0-585.0); g=0.82-(0.80*t) ; } if ((l>=400.0)&&(l<475.0)) { float t=(l-400.0)/(475.0-400.0); b= +(2.20*t)-(1.50*t*t); } else if ((l>=475.0)&&(l<560.0)) { float t=(l-475.0)/(560.0-475.0); b=0.7 -( t)+(0.30*t*t); } return fixed3(r,g,b); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

おわりに

このパートでは、シェーダーで虹のようなパターンを生成するための最も一般的な手法をいくつか見てきました。 次のパートでは、この問題を解決するための新しいアプローチを紹介します。

役職	勾配
ジェット機
ブルートン
GPUジェム
スペクター
ズッコニ
ズッコニ6
可視スペクトル

パート3.虹の改善-2。

はじめに

前のパートでは、電磁スペクトルの可視範囲（400〜700ナノメートル）の波長をそれぞれの色に変換する4つの異なる方法を分析しました。



これらのソリューションのうち3つ（JET、Bruton、およびSpektre）はif構造を積極的に使用します。 これはC＃の標準的な手法ですが、シェーダーでは分岐は悪いアプローチです。 分岐を使用しない唯一のアプローチは、GPU Gemsブックで説明されているアプローチです。 ただし、可視スペクトルの色の最適な近似値は提供されません。

役職	勾配
GPUジェム
可視スペクトル

このパートでは、GPU Gemsという本で説明されているカラースキームの最適化バージョンについて説明します。

バンプカラースキーム

GPU Gemsブックで概説されている元のカラースキームは、3つの放物線（著者によってバンプと呼ばれます ）を使用して、虹色のR、G、およびBコンポーネントの分布を再現します。









各バンプは、次の式で記述されます。

$$

$$bump \ left（x \ right）= \ left \ {\ begin {matrix} 0＆\ left | x \ right |> 1 \\ 1-x ^ 2＆\ mathit {otherwise} \ end {matrix} \ right 。$$

各波長 $$$w$ 範囲[400、700]は、正規化された値にマッピングされます $$$x$ 間隔[0,1]で。 次に、可視スペクトルの成分R、G、Bを次のように定義します。

$$

$$R \左（x \右）=バンプ\左（4 \ cdot x-0.75 \右）$$

$$

$$G \左（x \右）=バンプ\左（4 \ cdot x-0.5 \右）$$

$$

$$B \左（x \右）=バンプ\左（4 \ cdot x-0.25 \右）$$

すべての数値は、実験的に著者によって選択されています。 ただし、実際の色の分布にどれだけ対応していないかがわかります。

品質の最適化

私が最初に思いついた解決策では、GPU Gemsのカラースキームとまったく同じ方程式が使用されました。 ただし、すべての数値を最適化して、最終的な色の範囲が可能な限り可視スペクトルの実際の色と一致するようにしました。



結果は、次のソリューションに要約されます。









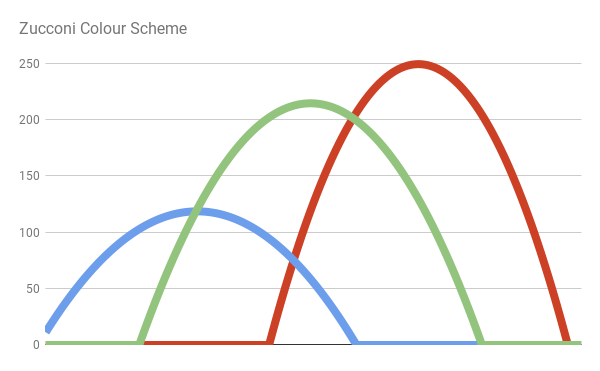
そして、より現実的な結果につながります。

役職	勾配
GPUジェム
ズッコニ
可視スペクトル

元のソリューションと同様に、新しいアプローチには分岐が含まれていません。 したがって、シェーダーに最適です。 コードは次のとおりです。

 //     GPU Gems //    inline fixed3 bump3y (fixed3 x, fixed3 yoffset) { float3 y = 1 - x * x; y = saturate(y-yoffset); return y; } fixed3 spectral_zucconi (float w) { // w: [400, 700] // x: [0, 1] fixed x = saturate((w - 400.0)/ 300.0); const float3 cs = float3(3.54541723, 2.86670055, 2.29421995); const float3 xs = float3(0.69548916, 0.49416934, 0.28269708); const float3 ys = float3(0.02320775, 0.15936245, 0.53520021); return bump3y ( cs * (x - xs), ys); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

虹の改善

可視スペクトルの色の分布を詳しく見ると、放物線は実際にはR、G、Bの色曲線を繰り返すことができないことに気付くでしょう。3つではなく6つの放物線を使用する方が良いでしょう。 各メインコンポーネントに2つのバンプを取り付けることにより、より正確な近似が得られます。 違いは、スペクトルの紫色の部分で非常に顕著です。









違いは、スペクトルの紫とオレンジの部分ではっきりと見えます。

役職	勾配
ズッコニ
ズッコニ6
可視スペクトル

コードは次のようになります。

 //     GPU Gems //    fixed3 spectral_zucconi6 (float w) { // w: [400, 700] // x: [0, 1] fixed x = saturate((w - 400.0)/ 300.0); const float3 c1 = float3(3.54585104, 2.93225262, 2.41593945); const float3 x1 = float3(0.69549072, 0.49228336, 0.27699880); const float3 y1 = float3(0.02312639, 0.15225084, 0.52607955); const float3 c2 = float3(3.90307140, 3.21182957, 3.96587128); const float3 x2 = float3(0.11748627, 0.86755042, 0.66077860); const float3 y2 = float3(0.84897130, 0.88445281, 0.73949448); return bump3y(c1 * (x - x1), y1) + bump3y(c2 * (x - x2), y2) ; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

spectrum_zucconi6が分岐せずに優れた色近似を提供することは間違いありません。 速度が重要な場合は、アルゴリズムの簡易バージョン-spectrum_zucconiを使用できます。

まとめると

このパートでは、シェーダーで虹のようなパターンを生成する新しいアプローチを検討しました。

役職	勾配
ジェット機
ブルートン
GPUジェム
スペクター
ズッコニ
ズッコニ6
可視スペクトル

パート4.回折格子を理解する

チュートリアルの最初の部分では、波と粒子の特性を示す光の二重の性質に精通しました。 このパートでは、なぜこれら2つの側面の両方が無差別の発生に必要であるかを見ていきます。

反射：光と鏡

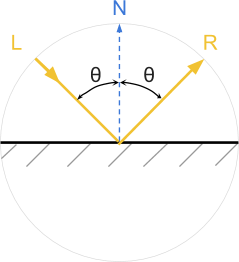
科学文献では、 光線は 、宇宙空間で光子が移動し、物体と相互作用する経路を示す方法としてしばしば言及されています。 ほとんどのシェーディングモデルでは、光は、完璧なビリヤードボールのように振る舞う均質な粒子から生成されると認識されます。 一般的な場合、光線が表面に衝突すると、同じ偏向角で反射します。 そのような表面は完全な鏡のように振る舞い、光を完全に反射します。









この手法を使用してレンダリングされたオブジェクトは、ミラーのようなものです。 さらに、光がL方向から落ちた場合、観察者はR方向から見たときにのみそれを見ることができます。 このタイプの反射は鏡面反射とも呼ばれ、鏡のような意味です。



現実の世界では、ほとんどのオブジェクトは拡散と呼ばれる異なる方法で光を反射します。 光線が散乱面に当たると、ほぼすべての方向に均一に散乱されます。 これにより、オブジェクトに均一な拡散色が与えられます。









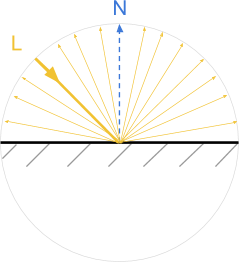
最新のエンジン（UnityやUnrealなど）では、これら2つの動作は異なる方程式のセットを使用してモデル化されます。 前回の物理ベースのレンダリングと照明モデルのチュートリアルでは、拡散反射と鏡面反射にそれぞれ使用されるランバート 反射モデルとブリンフォン 反射モデルについて説明しました。



異なって見えるという事実にもかかわらず、拡散反射はミラーを通して説明できます。 完全に平らな表面はありません。 小さな鏡から作成された粗い表面をシミュレートできます。各鏡は鏡面反射率によって完全に特徴付けられます。 そのような微小面の存在は、あらゆる方向の光線の散乱をもたらします。









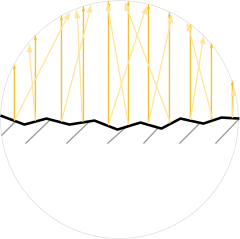
このようなマイクロファセットの多方向性は、多くの場合、 SmoothnessやRoughnessなどのプロパティを使用した物理的に正確なシェーダーによってモデル化されます。 この詳細については、Unityヘルプページで標準エンジンシェーダーのSmoothnessプロパティについて説明しています。

光は波のようです

光線がパーティクルで構成されているかのようにシミュレートすることは非常に便利です。 ただし、これにより、無差別を含む多くの資料を示す動作を再現することはできません。 特定の条件の光が波のように振る舞うという事実を受け入れた場合にのみ、いくつかの現象を完全に理解することができます。



ほとんどのシェーダーは、光をパーティクルとして使用します。 この大幅な簡素化の結果、 追加の構成が行われます。 2つの光線が観測者に到達した場合、それらの明るさは単純に加算されます。 サーフェスが放射する光線が多いほど、明るくなります。



現実の世界では、そうではありません。 2つの光線が観測者に到達する場合、最終的な色は、それらの波が相互作用する方法に依存します。 以下のアニメーションは、2つの単純な正弦波が位相に応じて互いに増幅または相殺 する方法を示しています。





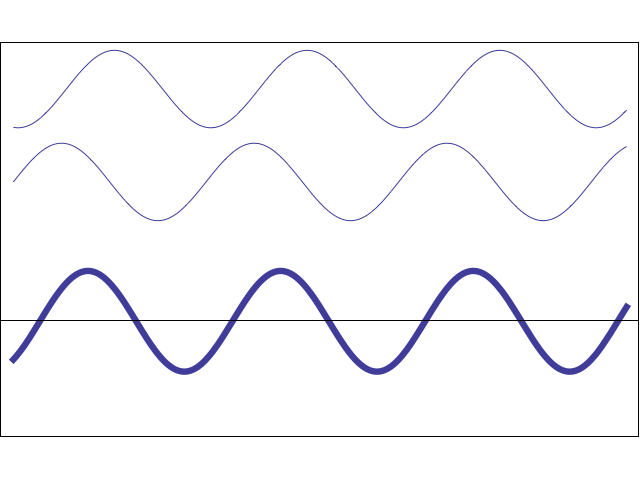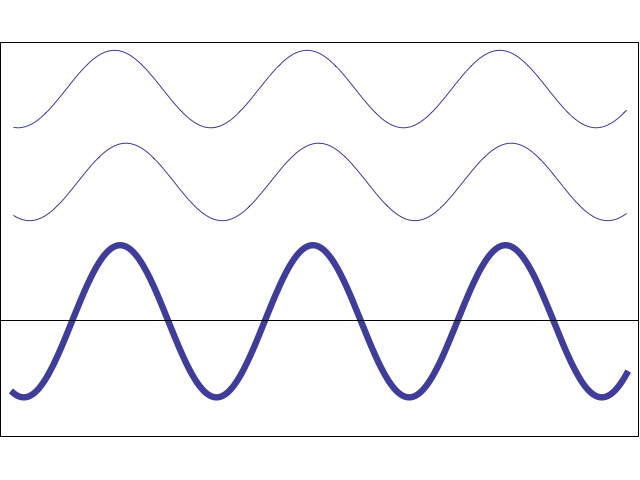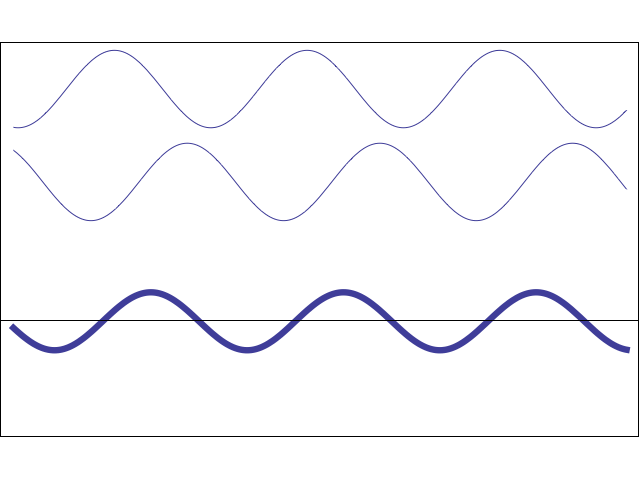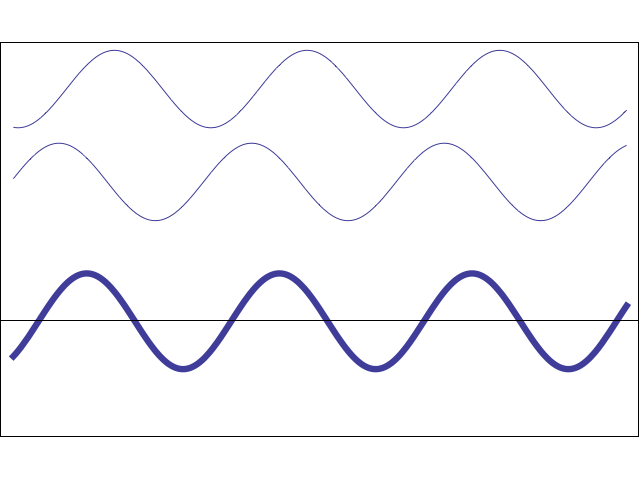
2つの波の位相が一致すると、そのピークと谷が理想的に一致します。この場合、最終的な波が増幅されます。 そうでなければ、彼らは文字通りお互いを破壊することができます。 これは、2つの光線が正しい構成で観測者に当たると、観測者が光を受け取らないことを意味します。



波の相互作用は奇妙な原理のように見えるかもしれません。 しかし、私たちは皆、日常生活でそれを経験しました。 科学の普及者であるデレク・ミュラーは、これを彼のビデオ「The Original Double Slit Experiment 」で説明しています。





しかし、これは光と虹色にどのように関係していますか？ 虹彩の理由は、異なる長さの光波の相互作用です。 一部のマテリアルは、正しい方向にのみフォトンを反射し、特定の色を強調し、他を破壊します。 この相互作用の結果として、虹を観察できます。

回折

このパートの最初のセクションでは、光と物質の相互作用のタイプの1つである反射について学習しました。 反射は、光が粒子としてモデル化されるときに発生します。 ただし、それを波のように扱うと、新しい一連の動作が発生します。 それらの1つは回折と呼ばれます。すべての入射光が同じ角度で表面に到達する場合、これは平面波と呼ばれます。たとえば、Unityの指向性光源は平面波を作成します。平面波がギャップを通過すると、次のアニメーションに示すように屈折します。





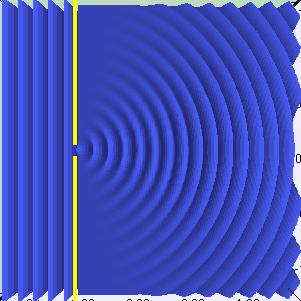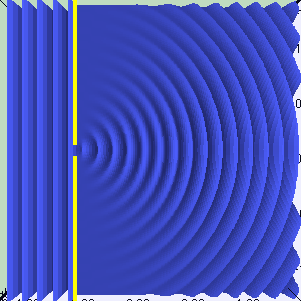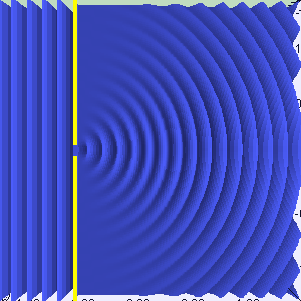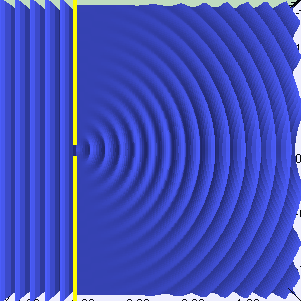
光が2つの異なるスリットを通過すると、2つの新しい波面が生成されます。そして、上で言ったように、これらの新しい光波は互いに相互作用することができます。以下のアニメーションは、このようなスロットが2つある場合のライトの動作を示しています。それらは実際に相互作用し、光線を増幅および消光することがわかります。





今、私たちは、無差別の原因を議論するために必要な基礎をすべて持っています。

回折格子

平面波がスリットを通過するか、粗さに反射すると、屈折し、新しい球面波面が作成されます。これは、拡散反射で発生するのと同様に、光がすべての方向に散乱されることを意味します。材料の表面が均一でない場合、結果として生じる平面波はランダムに散乱され、顕微鏡レベルで干渉パターンは発生しません。



ただし、一部の材料には、入射光の波長に匹敵するスケールで繰り返される表面パターンがあります。これが発生すると、パターンの再現性により、回折波の前面のランダムではない相互作用が繰り返されます。結果として生じる相互作用は、巨視的なレベルで見ることができる繰り返しの干渉パターンを作成します。



上記の効果は回折格子と呼ばれます。一部の波長は大幅に増幅され、他の波長は破壊されます。異なる波長が異なる色に対応するため、回折格子は、いくつかの色の反射がより顕著になるという事実につながります。



このメカニズムは、繰り返しパターンを持つ表面での虹彩の発生を提供します。それらは自然界にしばしば見られます。昆虫の外部骨格と鳥の羽には、繰り返しパターンで整列した顕微鏡スケールが含まれています。下の画像では、孔雀の羽の拡大画像が表示されています。

まとめると

チュートリアルの次の部分では、特定の種類の虹彩を数学的にモデル化する方法を示します。方程式を導出した後、シェーダーで簡単に実装できます。

パート5。回折格子の数学。

はじめに

前のパートでは、一部の素材で無差別が発生する理由について説明しました。これで、この現象を数学的にモデル化するために必要なものがすべて揃いました。既知の距離にわたって繰り返される不均一性がある素材を提示することから始めましょう$$$d$ 。 方程式を導き出すために、入射光線と表面法線の間の角度を次のように示します。 $$$\theta_L$ 。 また、観測者がすべての反射光線をある角度で受け取るように配置されていることを想像してみましょう $$$\theta_L$ 。 それぞれの不均一性は光をすべての方向に散乱させるため、観察者には常に関係なく光線が入射します $$$\theta_L$ 。









異質性は増分で定期的に繰り返されるため $$$d$ ナノメートル、その後散乱パターン自体が繰り返されます $$$d$ナノメートル。これは、各スリットから少なくとも1つの光線が観測者に到達することを意味します。

方程式の導出

上図に示されている2つの光線は、観測者に到達する前に異なる距離を進みます。これらの2つの光線の相互作用（相互の増幅または抑制）を理解するために、観測者に到達したときに位相が一致しない量を計算する必要があります。



これらの2つの光線は、最初の光線が表面に当たるまで位相が完全に一致します。2番目のビームは余分な距離を移動します$$$x$（緑色で強調表示）、その後表面にも落ちます。単純な三角法を使用して、緑の線の長さが$$$x$ 等しい $$$d \cdot \sin{\theta_L}$ 。









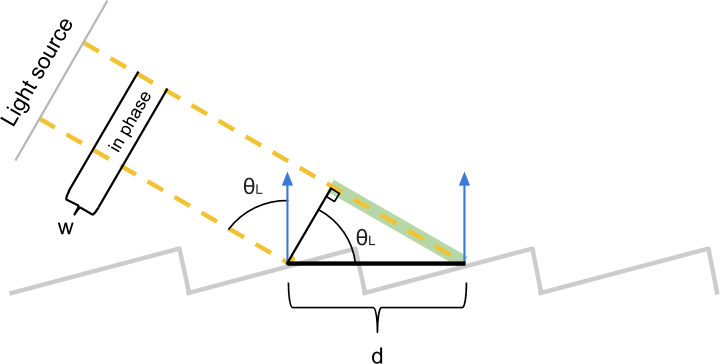
同様の構造を使用して、余分な距離を計算できます $$$y$、2番目のビームが表面に衝突するまで最初のビームを通過させます。この場合、次のことがわかります$$$y=d \cdot \sin{\theta_V}$ 。









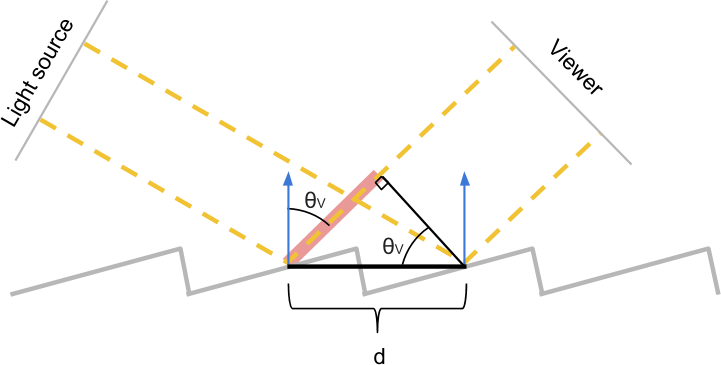
これら2つのセグメント $$$x$観測者が受信したときに2つのビームの位相が一致するかどうかを判断することが重要です。それらの違いは、これら2つの光線の長さの違いを測定します。ゼロに等しい場合、2つの光線は本質的に同じ距離を通過しているため、2つの光線の位相が一致していることが確実にわかります。



ただし、この場合だけでなく、2つの光線の位相が一致することもあります。長さの差が波長の整数倍である場合$$$w$その後、彼らはまだ同相になります。数学的な観点からは、2つの光線が次の条件を満たす場合、位相が一致します。

$$

$$d \sin{\theta_L} - d \sin{ \theta_V } = n \cdot w$$

$$

$$\sin{\theta_L} - \sin{ \theta_V } = \frac{n \cdot w}{d}$$

可視化

この方程式の意味を理解するために少し時間を取りましょう。光が斜めに落ちた場合$$$\theta_L$ 、材料を斜めから見たときに観察者が見るもの $$$\theta_V$ ？ すべての波長 $$$w$ 整数倍であること $$$d \left( \sin{\theta_L} - \sin{ \theta_V } \right)$、増幅と相互作用し、最終反射に強く現れます。したがって、視聴者に表示されるのはこれらの色です。



この効果は、複雑なアプローチの非常に興味深い議論から取られた次の図によって視覚化されています：サイクルの虹色：









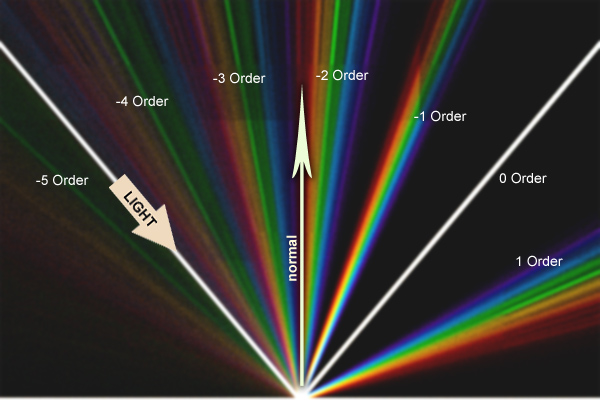
白い光線は、鏡面反射のために光子が続く経路をたどります。素材をさまざまな角度から見ると、円形の虹模様が見えます。各色はそれぞれの波長に対応し、順序によって対応する全体が決まります$$$n$ 。 ご覧のように、回折格子方程式は負の値でも満たされています $$$n$ 量のため $$$\sin{\theta_L} - \sin{ \theta_V }$負の値になる場合があります。計算の観点からは、検索空間を単純化して、正の値のみに制限することは理にかなっています$$$n$ 。 使用する新しい方程式は次のとおりです。

$$

$$\left | \sin{\theta_L} - \sin{ \theta_V } \right |= \frac{n \cdot w}{d}$$

パート6. CD-ROMシェーダー：回折格子-1

このパートでは、CD-ROMまたはDVDの表面に見える虹の反射を再現するシェーダーの作成について説明します。

はじめに

前のパートでは、いくつかの表面で示される虹彩反射の性質を記述する方程式を導き出しました。虹色は、表面に繰り返しパターンが存在する材料で発生し、そのサイズは、反射する光の波長に匹敵します。



最終的に再現したい光学効果は、光源と表面法線の間の角度（光の方向）、観察者の視角（視方向）、および繰り返されるギャップ間の距離の3つの要因に最終的に依存します。









シェーダーは、標準マテリアルが通常作成する通常の効果に虹色の反射を追加する必要があります。そのため、Standard Surfaceシェーダーのライティング機能を 拡張します。この手順に慣れていない場合は、チュートリアルのPhysically Based Rendering and Lighting Modelsを勉強する価値があります。

表面シェーダーの作成

最初のステップは、新しいシェーダーを作成することです。物理的に正確な照明を既にサポートしているシェーダーの機能を拡張したいので、標準の表面シェーダーから始めましょう。









作成されたCD-ROMシェーダーには、新しいプロパティdistanceが必要です。 $$$d$回折格子方程式で使用されます。ブロックに追加してみましょうProperties



。これは次のようになります。

 Properties { _Color ("Color", Color) = (1,1,1,1) _MainTex ("Albedo (RGB)", 2D) = "white" {} _Glossiness ("Smoothness", Range(0,1)) = 0.5 _Metallic ("Metallic", Range(0,1)) = 0.0 _Distance ("Grating distance", Range(0,10000)) = 1600 // nm }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そこで、マテリアルインスペクターに新しいスライダーを作成します。ただし、プロパティ_Distance



はセクション内の変数に関連付ける必要がありますCGPROGRAM



。

 float _Distance;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで作業する準備ができました。

照明機能を変更する

最初に行う必要があるのは、CD-ROMシェーダーのライティング機能を独自のものに置き換えることです。#pragma



ここでディレクティブを変更することでこれを行うことができます。

 #pragma surface surf Standard fullforwardshadows
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

に：

 #pragma surface surf Diffraction fullforwardshadows
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これにより、Unityはを呼び出した関数に照明計算を委任しLightingDiffraction



ます。このサーフェスシェーダーの機能を拡張し、再定義しないことを理解することが重要です。そのため、新しい照明機能は、標準のUnity PBR照明機能を呼び出すことから始まります。

 #include "UnityPBSLighting.cginc" inline fixed4 LightingDiffraction(SurfaceOutputStandard s, fixed3 viewDir, UnityGI gi) { //   fixed4 pbr = LightingStandard(s, viewDir, gi); // <    > return pbr; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

上記のコードスニペットからわかるように、新しい関数はLightingDiffraction



単にLightingStandard



その値を呼び出して返します。ここでシェーダーをコンパイルすると、マテリアルのレンダリング方法に違いは見られません。



ただし、先に進む前に、グローバルイルミネーションを処理するための追加の関数を作成する必要があります。この動作を変更する必要がないため、新しいグローバルライティング機能は、標準のUnity PBR機能のプロキシ機能にすぎません。

 void LightingDiffraction_GI(SurfaceOutputStandard s, UnityGIInput data, inout UnityGI gi) { LightingStandard_GI(s, data, gi); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

またLightingStandard



、直接使用LightingDiffraction_GI



するため、シェーダーに含める必要があることにも注意してくださいUnityPBSLighting.cginc



。

回折格子の実装

これがシェーダーの基礎になります。これで、前のパートで導出した回折格子方程式を実装する準備が整いました。その中で、観測者はすべての波長の合計である虹色の反射を見るという結論に達しました$$$w$格子方程式を満たす：

$$

$$\left | \sin{\theta_L} - \sin{ \theta_V } \right |= \frac{n \cdot w}{d}$$

どこで $$$n$ -より大きい整数 $$$0$ 。



各ピクセルについて、値 $$$\theta_L$（光の方向によって決定されます）、$$$\theta_V$（レビューの方向により決定）および$$$d$（ギャップ間の距離）は既知です。未知の変数は$$$w$ そして $$$n$ 。 最も簡単な方法は、値をループすることです $$$n$どの波長が格子方程式を満たすかを確認します。



最終的な虹色反射に寄与する波長がわかったら、それらに対応する色を計算して追加します。「虹の改善」セクションでは、可視スペクトルの波長を色に変換するいくつかの方法を検討しました。spectral_zucconi6



最小の計算コストで最良の近似を提供するため、このチュートリアルを使用します。



次の可能な実装を見てみましょう。

 inline fixed4 LightingDiffraction(SurfaceOutputStandard s, fixed3 viewDir, UnityGI gi) { //   fixed4 pbr = LightingStandard(s, viewDir, gi); //    fixed3 color = 0; for (int n = 1; n <= 8; n++) { float wavelength = abs(sin_thetaL - sin_thetaV) * d / n; color += spectral_zucconi6(wavelength); } color = saturate(color); //       pbr.rgb += color; return pbr; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このコードスニペットでは、値を使用します $$$n$より良い結果を得るために、より大きな値をとることができますが、これはすでに虹色の反射の重要な部分を考慮するのに十分です。



私たちは最後の左-計算するsin_thetaL



とsin_thetaV



。これを行うには、別の概念を導入する必要があります：接線ベクトルです。次のパートでは、その計算方法を学びます。

パート7.シェーダーCD-ROM：回折格子-2

はじめに

チュートリアルの前の部分で、CD-ROMの表面に現れる虹色の反射の最初の近似を作成しました。このシェーダーは物理的に正しいことを覚えておくことが重要です。必要な反射を正しくシミュレーションするには、CD-ROMのすべてのトラックが円状に配置されていることを確認する必要があります。これにより、放射状の反射が作成されます。

スロットの向き

導出したラティス方程式には大きな制限があります。すべてのスロットが同じ方向に配置されていることを前提としています。これは、外部の昆虫の骨格によく当てはまりますが、CD-ROMの表面のトラックは円形に配置されます。ソリューションを文字通り実装すると、かなり説得力のない反射が得られます（画像の右側）。









この問題を解決するには、CD-ROMのスロットのローカル方向を考慮する必要があります。すべてのスリットが同じ法線方向を持ち、ディスクの表面に垂直であるため、法線ベクトルを使用しても役に立ちません。スリットの局所的な向きは、接線ベクトル（上の画像の左側）を使用して決定できます。









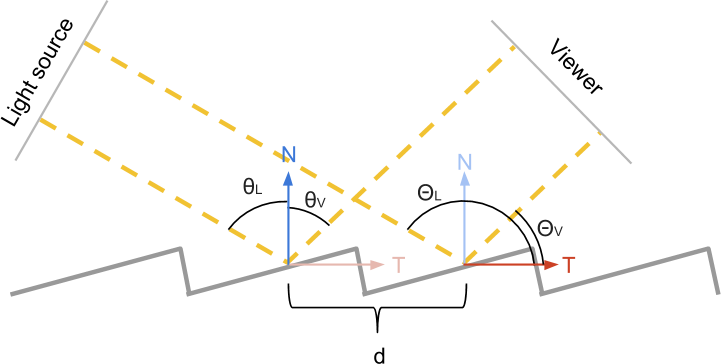
上の図では、法線方向 $$$N$ 青で表示され、接線の方向 $$$T$-赤。法線の方向で形成される光源と観察者の角度$$$N$ と呼ばれています $$$\theta_L$ そして $$$\theta_V$ 。 に似た角度 $$$T$ あれですか $$$\Theta_L$ そして $$$\Theta_V$ 。 上記のように、計算で使用される場合 $$$\theta_L$ そして $$$\theta_V$ すべてのスリットが同じであるため、「フラットな」反射が得られます $$$N$ 。 使用方法を見つける必要があります $$$\Theta_L$ そして $$$\Theta_V$、ローカル方向に正しく対応しているためです。



これまでのところ、次のことがわかっています。

$$

$$N \cdot L = \cos{\theta_L}\; \; \; N \cdot V = \cos{\theta_V}$$

$$

$$T \cdot L = \cos{\Theta_L}\; \; \; T \cdot V = \cos{\Theta_V}$$

以来 $$$T$ そして $$$N$ 垂直である場合、次のプロパティがあります。

$$

$$T \cdot L = \cos{\Theta_L} = \sin{\theta_L}$$

$$

$$T \cdot V = \cos{\Theta_V} = \sin{\theta_V}$$

Cgはスカラー積のネイティブ実装を提供するため、これも非常に便利です。計算するだけです$$$T$ 。

接線ベクトルの計算

シェーダーを終了するには、接線ベクトルを計算する必要があります $$$T$ 。通常、メッシュの上部に直接表示されます。ただし、CD-ROMの表面がどれほど単純かを考慮して、自分で計算することができます。このチュートリアルに示されているアプローチは非常に単純であり、CD-ROMメッシュの表面に正しいUVスキャンがある場合にのみ機能することを考慮する価値があります。









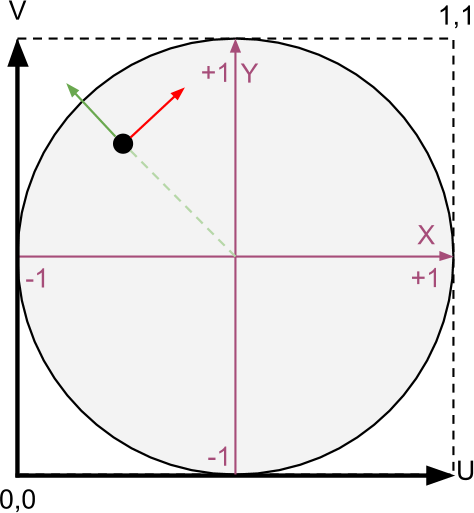
上の図は、接線の方向がどのように計算されるかを示しています。ディスクの表面は、座標が（0,0）から（1,1）の範囲の四角形としてUV現像されると想定されます。これを知って、CD-ROMの表面上の各ポイントの座標を（-1、-1）から（+1、+ 1）の範囲で再割り当てします。この原理を基礎として、点の新しい座標は中心から外側の方向にも対応していることがわかります（緑の矢印）。この方向を90度回転して、CD-ROMの同心円状のトラック（赤で表示）に接するベクトルを見つけることができます。









surf



UV座標はライティング関数では使用できないため、これらの操作はシェーダー関数で実行する必要がありますLightingDiffraction



。

 // IN.uv_MainTex: [ 0, +1] // uv: [-1, +1] fixed2 uv = IN.uv_MainTex * 2 -1; fixed2 uv_orthogonal = normalize(uv); fixed3 uv_tangent = fixed3(-uv_orthogonal.y, 0, uv_orthogonal.x);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

計算された接線をオブジェクトの空間からワールド空間に変換するだけです。変換では、オブジェクトの位置、回転、スケールが考慮されます。

 worldTangent = normalize( mul(unity_ObjectToWorld, float4(uv_tangent, 0)) );
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

すべてをまとめる

これで、虹色の反射に対する色の効果を計算するために必要なすべてができました。

 inline fixed4 LightingDiffraction(SurfaceOutputStandard s, fixed3 viewDir, UnityGI gi) { //   fixed4 pbr = LightingStandard(s, viewDir, gi); // ---    --- float3 L = gi.light.dir; float3 V = viewDir; float3 T = worldTangent; float d = _Distance; float cos_ThetaL = dot(L, T); float cos_ThetaV = dot(V, T); float u = abs(cos_ThetaL - cos_ThetaV); if (u == 0) return pbr; //   fixed3 color = 0; for (int n = 1; n <= 8; n++) { float wavelength = u * d / n; color += spectral_zucconi6(wavelength); } color = saturate(color); //      pbr.rgb += color; return pbr; }