パート1.環境の作成
エージェントが動作する環境は、サイズnの2次元フィールドで表されます。 これはどのように見えるかです:
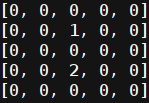
ここで、ユニットはエージェントを表し、デュースで敵を表します。 次に、コードに直接目を向けます。 環境を説明する変数:フィールドサイズ、エージェント、敵のリスト。
環境クラス
class W: def __init__(self,n): self.n=n self.P=P(1,1,n) self.ens=[EN(3,3,n),EN(4,4,n),EN(5,5,n)]
タイプアクター:エージェントまたは敵。
俳優クラス
class un: def __init__(self,x,y): self.x = x self.y = y def getxy(self): return self.x, self.y
エージェントの説明。
エージェントクラス
class P(un): def __init__(self,x,y,n): self.n=n un.__init__(self,x,y)
エージェント戦略はまだ空です。
メソッド呼び出しエージェント戦略
def strtg(self): return 0,0
シミュレーションの各参加者は、斜めを含む任意の方向に移動できますが、俳優もまったく移動しない場合があります。 敵の例で許可された一連の動き:
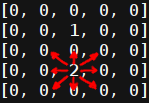
対角線に沿った動きのおかげで、敵はどのように離れようとしても、常にエージェントを追い越す機会があります。 これにより、エージェントのトレーニングの程度に関係なく、有限数のシミュレーション移動が提供されます。 バイアスの有効性をチェックしながら、考えられるアクションを書き留めます。 このメソッドは、エージェントの座標の変更を受け入れ、その位置を更新します。
エージェント移動方法
def move(self): dx,dy=self.strtg() a=self.x+dx b=self.y+dy expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b
敵の説明。
敵のクラス
class EN(un): def __init__(self,x,y,n): self.n=n un.__init__(self,x,y)
変位の許容性の検証で敵を移動します。 このメソッドは、ストロークの有効性の条件が満たされるまでサイクルを終了しません。
敵の移動方法
def move(self): expr=False while not expr: a=self.x+random.choice([-1,0,1]) b=self.y+random.choice([-1,0,1]) expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b
ワンステップシミュレーション。 敵とエージェントの位置を更新する
環境メソッド、次のシミュレーションステップを拡張
def step(self): for i in self.ens: i.move() self.P.move()
シミュレーションの可視化。
環境メソッド、フィールドの描画およびアクターの位置
def pr(self): print('\n'*100) px,py=self.P.getxy() self.wmap=list([[0 for i in range(self.n)] for j in range(self.n)]) self.wmap[py][px]=1 for i in self.ens: ex,ey=i.getxy() self.wmap[ey][ex]=2 for i in self.wmap: print(i)
シミュレーション、主な段階:
1.俳優の座標の登録。
2.シミュレーションの完了条件の達成の検証。
3.シミュレーションの移動を更新するサイクルの開始。
-描画環境。
-シミュレーション状態を更新します。
-俳優の座標の登録。
-シミュレーションの完了条件の達成の検証。
4.環境を描画します。
環境メソッド、シミュレーションシーケンスの再生
def play(self): px,py=self.P.getxy() bl=True for i in self.ens: ex,ey=i.getxy() bl=bl and (px,py)!=(ex,ey) iter=0 while bl: time.sleep(1) wr.pr() self.step() px,py=self.P.getxy() bl=True for i in self.ens: ex,ey=i.getxy() bl=bl and (px,py)!=(ex,ey) print((px,py),(ex,ey)) print('___') iter=iter+1 print(iter)
環境の初期化と起動。
シミュレーションを実行する
if __name__=="__main__": wr=W(7) wr.play() wr.pr()
パート2.エージェントトレーニング
q学習法は関数Qの導入に基づいています。これは、現在の状態sのエージェントが可能なアクションの値を反映しており、その中にシミュレーションが配置されています。 または簡単に:
Q(s、a)
この関数は、エージェントが特定の動きで特定のアクションを完了することで受け取ることができる報酬の評価を設定します。 また、エージェントが将来受け取る報酬の評価も含まれます。 学習プロセスは、エージェントの各ターンでの関数Qの値の反復的な改良です。 まず、エージェントがこのターンに受け取る報酬の量を決定する必要があります。 変数に書きましょう rt 。 次に、後続の移動で予想される最大報酬を決定します。
maxaQ(st+1、a)
ここで、エージェントにとって大きな価値があるもの、つまり一時的な報酬または将来の報酬を決定する必要があります。 この問題は、後続の賞のコンポーネント評価における追加要因によって解決されます。 結果として、このステップでエージェントによって予測される関数Qの値は、可能な限り値に近いはずです。
rt+ gamma cdot maxaQ(st+1、a)
したがって、エージェントの現在の動きに対する関数Qの予測エラーは次のように記述されます。
Deltaq=rt+ gamma cdot maxaQ(st+1、a)−Q(st、at)
エージェントのトレーニング率を調整する係数を導入します。 関数Qを繰り返し計算するための式は次の形式になります。
Q(st+1、at+1)=Q(st、at)+ alpha cdot Deltaq
関数Qの反復計算の一般式:
Q(st+1、at+1)=Q(st、at)+ alpha cdot(rt+ gamma cdot maxaQ(st+1、a)−Q(st、at))
エージェントの観点から環境の説明を構成する主な機能を選び出します。 パラメータのセットが広いほど、環境の変化に対する応答がより正確になります。 同時に、状態空間のサイズは学習速度に大きく影響する可能性があります。
エージェントメソッド、環境の状態を示す記号
def get_features(self,x,y): features=[] for i in self.ens: #800-1400 ex,ey=i.getxy() features.append(ex) features.append(ey) features.append(x) features.append(y) return features
クラスQモデルの作成。 可変ガンマ-後続の賞の貢献度を平準化できる減衰係数。 変数alphaはモデル学習率係数です。 状態変数-モデル状態辞書。
クラスQモデル
class Q: def __init__(self): self.gamma=0.95 self.alpha=0.05 self.state={}
このターンのエージェントの状態を取得します。
モデルのQメソッドは、要求に応じて、エージェントの状態を受け取ります
def get_wp(self,plr): self.plr=plr
モデルをトレーニングします。
Qモデル法、モデルトレーニングの1段階
def run_model(self,silent=1): self.plr.prev_state=self.plr.curr_state[:-2]+(self.plr.dx,self.plr.dy) self.plr.curr_state=tuple(self.plr.get_features(self.plr.x,self.plr.y))+( self.plr.dx,self.plr.dy) if not silent: print(self.plr.prev_state) print(self.plr.curr_state) r=self.plr.reward if self.plr.prev_state not in self.state: self.state[self.plr.prev_state]=0 nvec=[] for i in self.plr.actions: cstate=self.plr.curr_state[:-2]+(i[0],i[1]) if cstate not in self.state: self.state[cstate]=0 nvec.append(self.state[cstate]) nvec=max(nvec) self.state[self.plr.prev_state]=self.state[self.plr.prev_state]+self.alpha*(-self.state[self.plr.prev_state]+r+self.gamma*nvec)
賞を獲得する方法。 エージェントには、シミュレーションの継続に対する報酬が与えられます。 このペナルティは、敵との衝突に対して認められます。
環境法、賞のサイズ決定
def get_reward(self,end_bool): if end_bool: self.P.reward=1 else: self.P.reward=-1
エージェント戦略。 モデル状態ディクショナリから最適な値を選択します。 epsクラスがエージェントクラスに追加され、移動を選択するときにランダム性の要素が導入されました。 これは、この状態で関連する可能なアクションを調査するために行われます。
エージェント方式、次の移動の選択
def strtg(self): if random.random()<self.eps: act=random.choice(self.actions) else: name1=tuple(self.get_features(self.x,self.y)) best=[(0,0),float('-inf')] for i in self.actions: namea=name1+(i[0],i[1]) if namea not in self.QM.state: self.QM.state[namea]=0 if best[1]<self.QM.state[namea]: best=[i,self.QM.state[namea]] act=best[0] return act
シミュレーションの状態に関する情報の完全な転送(エージェントの絶対座標、敵の絶対座標)により、エージェントが何を学んだかを示します。
アルゴリズムの結果(GIF〜1Mb) 
パート3.エージェントの環境の状態を反映するパラメーターを変更します
まず、エージェントが環境に関する情報をまったく受け取らない状況を考えます。
機能1
def get_features(self,x,y): features=[] return features
このようなアルゴリズムの操作の結果、エージェントはシミュレーションごとに平均40〜75ポイントを獲得します。 トレーニングスケジュール:
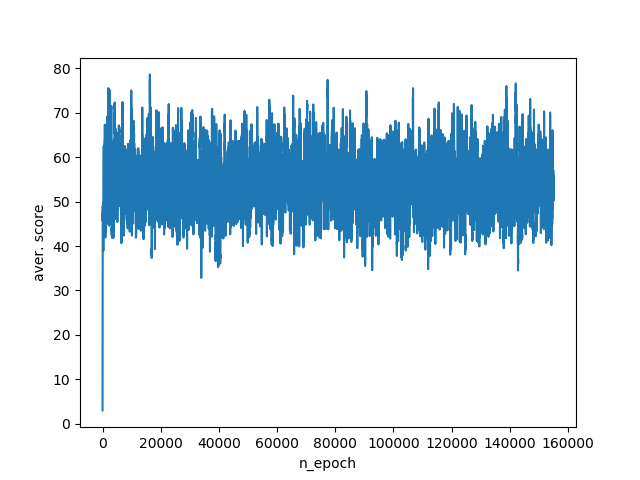
データエージェントに追加します。 まず第一に、敵がどれだけ遠くにあるかを知る必要があります。 ユークリッド距離を使用してこれを計算します。 また、エージェントがどの程度接近したかを把握することも重要です。
機能2
def get_features(self,x,y): features=[] for i in self.ens: ex,ey=i.getxy() dx=abs(x-ex) dy=abs(y-ey) l=hypot(dx,dy) features.append(l) to_brdr=min(x,y,self.n-1-x,self.n-1-y) features.append(to_brdr) return features
この情報を考慮すると、エージェントのスコアがシミュレーションごとに20ポイント低くなり、平均スコアは60〜100ポイントの範囲になります。 環境の変化への対応が改善されたという事実にもかかわらず、私たちはまだ必要なデータの大部分を失っています。 そのため、エージェントは、敵との距離を空けるために、またはエッジの端から離れるためにどの方向に移動するかをまだ知りません。 トレーニングスケジュール:
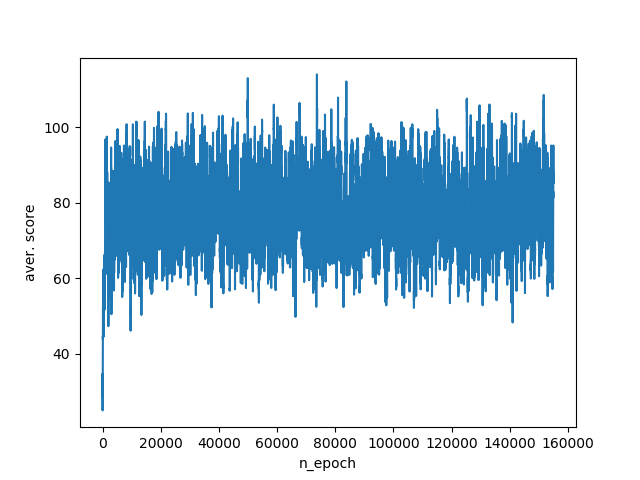
次のステップは、敵が敵のどちら側にいるのか、エージェントがフィールドの端にいるかどうかをエージェントに追加することです。
機能3
def get_features(self,x,y): features=[] for i in self.ens: ex,ey=i.getxy() features.append(x-ex) features.append(y-ey) # if near wall x & y. if x==0: features.append(-1) elif x==self.n-1: features.append(1) else: features.append(0) if y==0: features.append(-1) elif y==self.n-1: features.append(1) else: features.append(0) return features
このような変数のセットは、ポイントの平均数をすぐに400〜800に大幅に増やします。 トレーニングスケジュール:
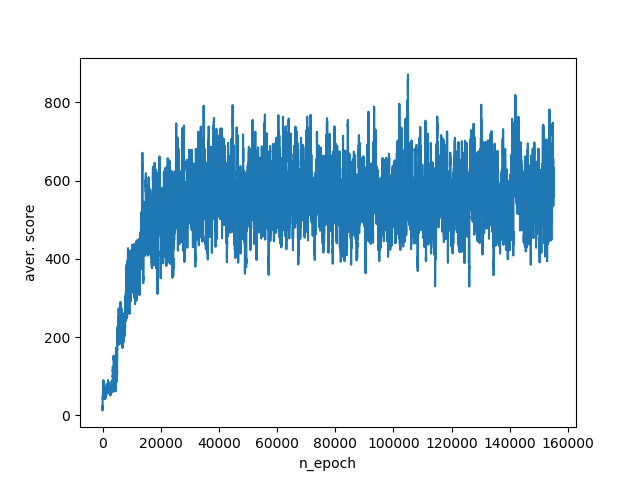
最後に、アルゴリズムに環境に関する利用可能なすべての情報を提供します。 つまり、エージェントと敵の絶対座標。
機能4
def get_features(self,x,y): features=[] for i in self.ens: ex,ey=i.getxy() features.append(ex) features.append(ey) features.append(x) features.append(y) return features
このパラメーターセットにより、エージェントはテストシミュレーションで800〜1400ポイントを獲得できます。 トレーニングスケジュール:
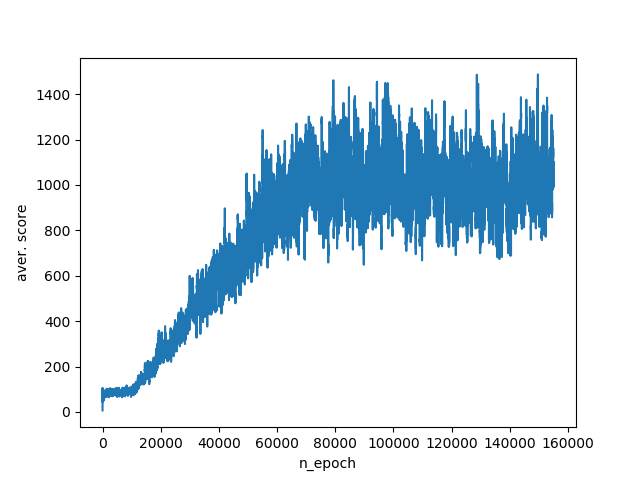
そこで、q-learningアルゴリズムの動作を調べました。 エージェントが環境を知覚する原因となるパラメーターをひねりながら、情報を適切に転送し、環境を説明するときにすべての側面を考慮すると、その行動の効果にどのように影響するかが明確にわかりました。 ただし、環境の完全な説明には欠点があります。 つまり、エージェントに送信される情報量の増加に伴う状態空間の爆発的な成長。 この問題を回避するために、たとえばDQNアルゴリズムなど、状態空間を近似するアルゴリズムが開発されました。
便利なリンク:
habrahabr.ru/post/274597
ai.berkeley.edu/reinforcement.html
プログラムの完全なコード:
1.環境の基本モデル(パート1から)
import random import time class W: def __init__(self,n): self.n=n self.P=P(1,1,n) self.ens=[EN(3,3,n),EN(4,4,n),EN(5,5,n)] def step(self): for i in self.ens: i.move() self.P.move() def pr(self): print('\n'*100) px,py=self.P.getxy() self.wmap=list([[0 for i in range(self.n)] for j in range(self.n)]) self.wmap[py][px]=1 for i in self.ens: ex,ey=i.getxy() self.wmap[ey][ex]=2 for i in self.wmap: print(i) def play(self): px,py=self.P.getxy() bl=True for i in self.ens: ex,ey=i.getxy() bl=bl and (px,py)!=(ex,ey) iter=0 while bl: time.sleep(1) wr.pr() self.step() px,py=self.P.getxy() bl=True for i in self.ens: ex,ey=i.getxy() bl=bl and (px,py)!=(ex,ey) print((px,py),(ex,ey)) print('___') iter=iter+1 print(iter) class un: def __init__(self,x,y): self.x = x self.y = y def getxy(self): return self.x, self.y class P(un): def __init__(self,x,y,n): self.n=n un.__init__(self,x,y) def strtg(self): return 0,0 def move(self): dx,dy=self.strtg() a=self.x+dx b=self.y+dy expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b class EN(un): def __init__(self,x,y,n): self.n=n un.__init__(self,x,y) def move(self): expr=False while not expr: a=self.x+random.choice([-1,0,1]) b=self.y+random.choice([-1,0,1]) expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b if __name__=="__main__": wr=W(7) wr.play() wr.pr()
2. 500 + 1500のシミュレーションでエージェントトレーニングを行う環境モデル
import random import time from math import hypot,pi,cos,sin,sqrt,exp import plot_epoch class Q: def __init__(self): self.gamma=0.95 self.alpha=0.05 self.state={} def get_wp(self,plr): self.plr=plr def run_model(self,silent=1): self.plr.prev_state=self.plr.curr_state[:-2]+(self.plr.dx,self.plr.dy) self.plr.curr_state=tuple(self.plr.get_features(self.plr.x,self.plr.y))+(self.plr.dx,self.plr.dy) if not silent: print(self.plr.prev_state) print(self.plr.curr_state) r=self.plr.reward if self.plr.prev_state not in self.state: self.state[self.plr.prev_state]=0 nvec=[] for i in self.plr.actions: cstate=self.plr.curr_state[:-2]+(i[0],i[1]) if cstate not in self.state: self.state[cstate]=0 nvec.append(self.state[cstate]) nvec=max(nvec) self.state[self.plr.prev_state]=self.state[self.plr.prev_state]+self.alpha*( -self.state[self.plr.prev_state]+r+self.gamma*nvec) class un: def __init__(self,x,y): self.x = x self.y = y self.actions=[(0,0),(-1,-1),(0,-1),(1,-1),(-1,0), (1,0),(-1,1),(0,1),(1,1)] def getxy(self): return self.x, self.y class P(un): def __init__(self,x,y,n,ens,QM,wrld): self.wrld=wrld self.QM=QM self.ens=ens self.n=n self.dx=0 self.dy=0 self.eps=0.95 self.prev_state=tuple(self.get_features(x,y))+(self.dx,self.dy) self.curr_state=tuple(self.get_features(x,y))+(self.dx,self.dy) un.__init__(self,x,y) def get_features(self,x,y): features=[] # for i in self.ens: #80-100 # ex,ey=i.getxy() # dx=abs(x-ex) # dy=abs(y-ey) # l=hypot(dx,dy) # features.append(l) # to_brdr=min(x,y,self.n-1-x,self.n-1-y) # features.append(to_brdr) for i in self.ens: #800-1400 ex,ey=i.getxy() features.append(ex) features.append(ey) features.append(x) features.append(y) # for i in self.ens: #800-1400 # ex,ey=i.getxy() # features.append(x-ex) # features.append(y-ey) # features.append(self.n-1-x) # features.append(self.n-1-y) # for i in self.ens: #400-800 # ex,ey=i.getxy() # features.append(x-ex) # features.append(y-ey) # # if near wall x & y. # if x==0: # features.append(-1) # elif x==self.n-1: # features.append(1) # else: # features.append(0) # if y==0: # features.append(-1) # elif y==self.n-1: # features.append(1) # else: # features.append(0) # features=[] #40-80 return features def strtg(self): if random.random()<self.eps: act=random.choice(self.actions) else: name1=tuple(self.get_features(self.x,self.y)) best=[(0,0),float('-inf')] for i in self.actions: namea=name1+(i[0],i[1]) if namea not in self.QM.state: self.QM.state[namea]=0 if best[1]<self.QM.state[namea]: best=[i,self.QM.state[namea]] act=best[0] return act def move(self): self.dx,self.dy=self.strtg() a=self.x+self.dx b=self.y+self.dy expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b class EN(un): def __init__(self,x,y,n): self.n=n un.__init__(self,x,y) def move(self): expr=False cou=0 while not expr: act=random.choice(self.actions) a=self.x+act[0] b=self.y+act[1] expr=((0<=a<self.n) and (0<=b<self.n)) if expr: self.x=a self.y=b class W: def __init__(self,n,QModel): self.ens=[EN(n-2,n-2,n)]#,EN(n-2,n-1,n),EN(n-1,n-2,n),EN(n-1,n-1,n)] self.P=P(1,1,n,self.ens,QModel,self) self.n=n self.QM=QModel self.QM.get_wp(self.P) def step(self): self.P.move() for i in self.ens: i.move() def pr(self,silent=1): """print map""" #print('\n'*100) px,py=self.P.getxy() self.wmap=list([[0 for i in range(self.n)] for j in range(self.n)]) self.wmap[py][px]=1 for i in self.ens: ex,ey=i.getxy() self.wmap[ey][ex]=2 if not silent: for i in self.wmap: print(i) def is_finished(self): px,py=self.P.getxy() end_bool=True for i in self.ens: ex,ey=i.getxy() end_bool=end_bool and ((px,py)!=(ex,ey)) return end_bool def get_reward(self,end_bool): if end_bool: self.P.reward=1 else: self.P.reward=-1 def play(self,silent=1,silent_run=1): end_bool=self.is_finished() iter=0 while end_bool: self.pr(silent) self.step() end_bool=self.is_finished() self.get_reward(end_bool) if silent_run: self.QM.run_model(silent) if not silent: print('___') time.sleep(0.1) iter=iter+1 return iter QModel=Q() plot=plot_epoch.epoch_graph() for i in range(500): wr=W(5,QModel) wr.P.eps=0.90 iter=wr.play(1) wr.pr(1) plot.plt_virt_game(W,QModel) for i in range(1500): wr=W(5,QModel) #print(len(QModel.state)) wr.P.eps=0.2 iter=wr.play(1) wr.pr(1) plot.plt_virt_game(W,QModel) plot.plot_graph() print('___') for i in range(10): wr=W(5,QModel) wr.P.eps=0.0 iter=wr.play(0) wr.pr(0)
3.チャート出力モジュール(plot_epoch.py)。
import matplotlib.pyplot as plt class epoch_graph: def __init__(self): self.it=0 self.iter=[] self.number=[] self.iter_aver=[] def plt_append(self,iter): self.it=self.it+1 self.iter.append(iter) self.number.append(self.it) if len(self.iter)>100: self.iter_aver.append(sum(self.iter[-100:])/100) else: self.iter_aver.append(sum(self.iter)/len(self.iter)) def plt_virt_game(self,W,QModel): wr=W(5,QModel) wr.P.eps=0.0 iter=wr.play(1,0) self.plt_append(iter) def plot_graph(self): plt.plot(self.number,self.iter_aver) plt.xlabel('n_epoch') plt.ylabel('aver. score') plt.show()