この記事は、javarevisitedブログ記事の翻訳です。 面接の準備として、初心者と経験豊富なプログラマの両方が興味を持つ場合があります。 将来的には、典型的な問題と学術的な問題の両方を解決するためのアルゴリズムとレシピに関する一連の記事を翻訳する予定です。 翻訳の品質と新しい記事の選択の両方について、建設的な提案とコメントを受け付けています。
単純に接続されたリストの最後から3番目の要素または末尾からn番目のノードを見つけることは、インタビューでの単純に接続されたリストの問題に関する難しい質問の1つです。 この場合のタスクは、サイクルの1回のパスで問題を解決することです。つまり、リンクリストを再度たどることができず、反対方向に進むことができません。 リストは単純に接続されています。 長さの検索 、アイテムの挿入または削除など、リンクリストの問題を解決したことがある場合は、クロールリストの問題について既に理解している必要があります。 この記事では、ループの1つのパスでリンクリストの中間要素を見つけるために使用したものと同じアルゴリズムを使用します 。 このアルゴリズムは、単一リンクリストをトラバースするためにアルゴリズムで使用される2つのポインターの速度のため、 「亀とうさぎのアルゴリズム」とも呼ばれます。
覚えているなら、アルゴリズムは2つのポインター-高速と低速を使用します。 スローポインターは高速がN番目の要素に到達するとクロールを開始します。たとえば、最後から3番目の要素を見つけるために、最初のポインターが3番目の要素に到達すると2番目のポインターがクロールを開始します。
その後、最初のポインターがリンクリストの終わりを示すnullを指すまで、両方のポインターが反復ごとに1ステップ移動します 。 この時点で、2番目のポインターは最後から3番目またはN番目のノードを指します。 問題は解決し、ノードの値を表示するか、要件に応じて呼び出し元にリンクを返すことができます。
これは、典型的なインタビューで遭遇する多くのデータ構造の問題とアルゴリズムの問題の1つです( コーディングインタビューのクラックを参照)。 リンクリストは一般的なデータ構造であるため、リンクリストのループと長さの決定に関する質問、およびこの記事で取り上げた質問は非常に人気があります。
リンクリストの末尾からn番目のノードを見つけるためのJavaプログラム
以下は、単一リンクリストの最後からN番目の要素を見つけるためのJavaプログラムの完全なリストです。 このプログラムは、1回のパスで問題を解決します。つまり、リンクリストは1回だけクロールされます。 ご覧のとおり、getLastNode(int n)メソッドでwhileループを1つだけ使用しました。 このメソッドは整数パラメーターを受け取り、リンクされたリストの末尾からn番目の要素を見つけるために使用できます。たとえば、末尾から2番目の要素の場合、2ステップが必要で、リストの3番目の要素を取得します。
SinglyLinkedListクラスは、Javaの単一リンクリストです。 これは、たとえばJavaでリンクリストを実装する場合など、単一リンクリストに関する記事で以前に使用したものと同じクラスです。 これは、リンクリストノードであるNodeクラスのコレクションです。 データと次のノードへのリンクが含まれています。 SinglyLinkedListクラスには、ヘッド参照も含まれています。 リンクリストの最初のノード 。
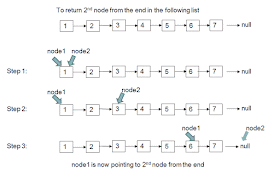
以下は、単純に接続されたリストの末尾から2番目の要素を見つける視覚的な説明です。 ファストポインタとスローポインタがリストをどのように通過するかを確認できます。ファストポインタがテールを指すと、スローポインタは最後からn番目のノードを指します。
プログラマーとして、基本的なデータ構造とアルゴリズム、たとえばリンクリストとは何か、その長所と短所を知っておく必要があります。また、それを使用する場合は、たとえば、要素を頻繁に追加および削除するのに適していますが、検索にはあまり適していません。 。 リンクリスト内のアイテムを見つけるには、O(n)時間かかります。 リンクされたリストの詳細については、データ構造とアルゴリズムに関する優れた書籍(トーマスH.コーメンによるアルゴリズムの紹介など)を参照してください。
最初は、この本が好きではないかもしれません。トピックとプレゼンテーションのスタイルのために理解するのが少し難しいからです。しかし、それに沿って時々参照し、配列、リンクリスト、ツリーなどの主要なデータ構造を理解する必要がありますなど
単純に接続されたリストの最後からN番目のノード
public class Practice { public static void main(String args[]) { SinglyLinkedList list = new SinglyLinkedList(); list.append("1"); list.append("2"); list.append("3"); list.append("4"); System.out.println(" : " + list); System.out.println(" : " + list.getLastNode(1)); System.out.println(" : " + list.getLastNode(2)); System.out.println(" : " + list.getLastNode(3)); } } /** * Java * * @author Javin * */ class SinglyLinkedList { static class Node { private Node next; private String data; public Node(String data) { this.data = data; } @Override public String toString() { return data.toString(); } } private Node head; // - /** * , * * @ true , .., */ public boolean isEmpty() { return length() == 0; } /** * * * @param data */ public void append(String data) { if (head == null) { head = new Node(data); return; } tail().next = new Node(data); } /** * * * @return */ private Node tail() { Node tail = head; // , while (tail.next != null) { tail = tail.next; } return tail; } /** * * * @return , ., */ public int length() { int length = 0; Node current = head; while (current != null) { length++; current = current.next; } return length; } /** * n- * * @param n * @return n- */ public String getLastNode(int n) { Node fast = head; Node slow = head; int start = 1; while (fast.next != null) { fast = fast.next; start++; if (start > n) { slow = slow.next; } } return slow.data; } @Override public String toString() { StringBuilder sb = new StringBuilder(); Node current = head; while (current != null) { sb.append(current).append("-->"); current = current.next; } if (sb.length() >= 3) { sb.delete(sb.length() - 3, sb.length()); } return sb.toString(); } }
おわりに
リンクリスト:1-> 2-> 3-> 4
最後から最初の結び目:4
最後から2番目の結び目:3
尾から3番目の結び目:
これは、Javaのリンクリストの最後から3番目の要素を見つけることです。 うさぎとカメのアルゴリズムとしても知られる2ポインターアプローチを使用して、1回のパスで問題を解決するプログラムを作成しました。 1つのポインターが2番目のポインターよりも遅い。 これは便利なトリックの1つです。なぜなら、 ここに示すように、同じアルゴリズムを使用してリンクリストのループを決定できます。 リンクされたリストをクロールし、同時にノードを操作する必要がある場合、このアルゴリズムを使用して創造的に他の問題を解決することもできます。