ブライテンベルク機械シミュレーター

Breitenberg車のシミュレーターを書きたかっただけです。 このことのルーツは、単純なロボットを構築するという考えに基づいていますが、複雑なシステムの開発という観点からも興味深いものです。









それで何ですか？



（注意、記事には多くの写真とアニメーションがあります！）



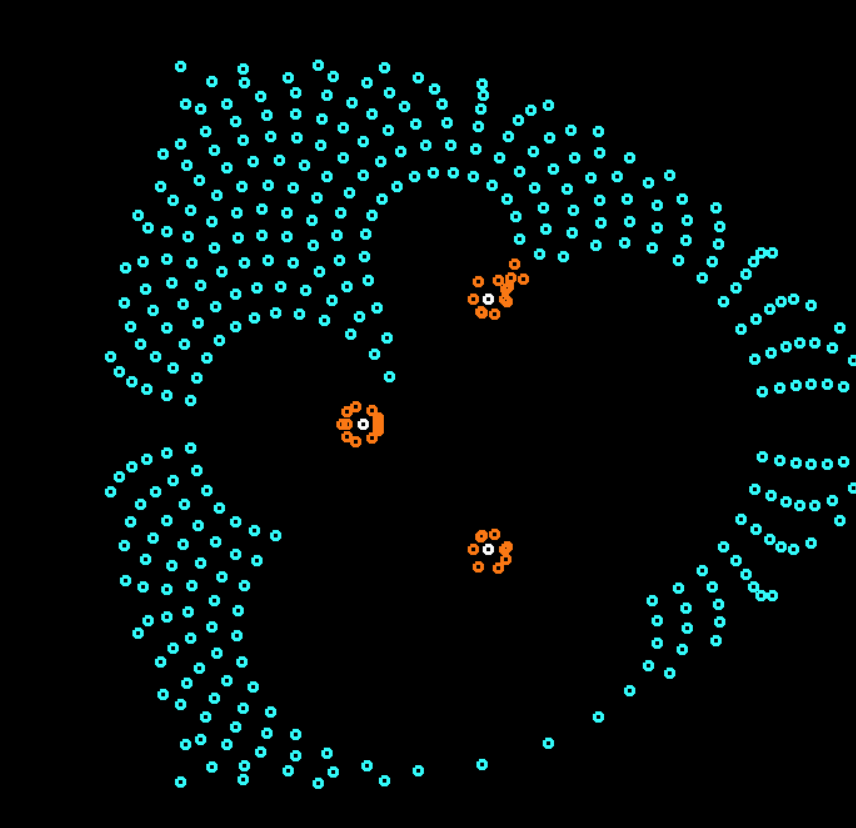
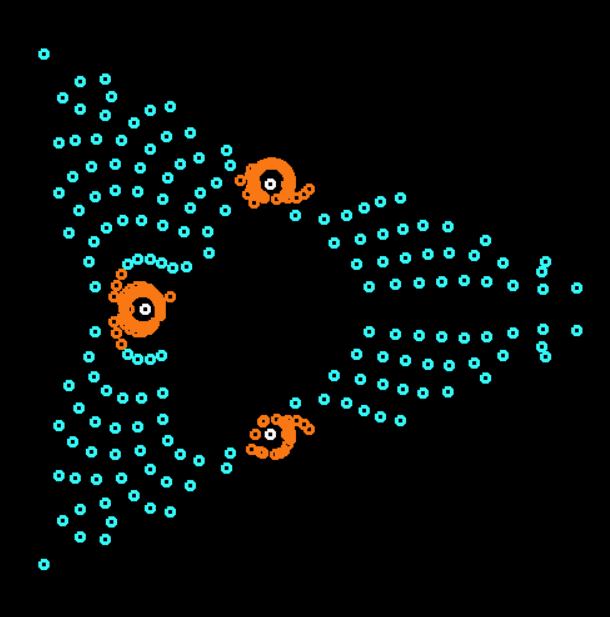
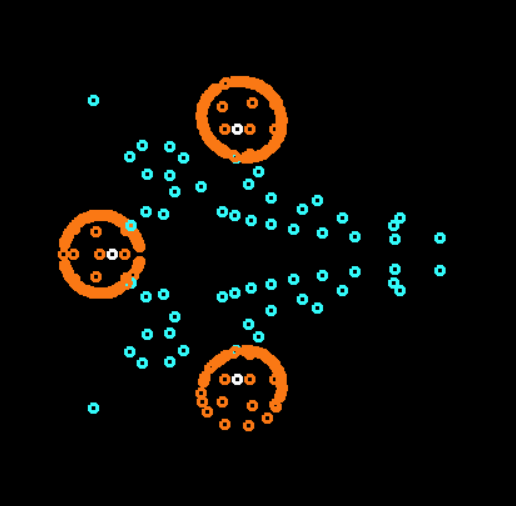
Breitenbergタイプライターは、最小数の要素の最も単純なロジックに基づくオートマトンですが、外部の観察者が合理的なものとして受け入れることができる複雑な動作を示します（単純な外観は複雑な「見せびらかす」ロボットのようです）。

それらは、 neurodeと呼ばれる特定のデザインに基づいて、6つのタイプで説明されています 。 ニューロンは、出力のパルス数に影響を与えるブレーキ信号または加速信号を受信できます。 そのようなニューロンのニューラルネットワーク（最も単純な場合でも2〜8個の要素）は、いくつかの基本的な動作パターンを作成できます。 自動機の動作原理は次のとおりです。



センサー（光に反応する）->神経細胞のネットワーク->アクチュエーター（モーター）



最初のタイプの動作、最も単純な-ニューロンがなく、センサー信号がモーターに直接送られる場合。 次に、左目が左のモーターをねじるほど明るくなり、右も同じです。 そのようなシステムは、光から「逃げる」でしょう。



コンダクターを交差させると（左目から右モーターへ、およびその逆）、光を好むロボットが得られ、加速して電球に到達します。 他のタイプについては、モデル化されるにつれて詳細に説明されます。



これらの6種類の車の群れを電球のある部屋に置くことは（ブライテンベルクによって）想定されていたので、観察者（仮想のロボット心理学者）はその動きに複雑な行動を見ます。 そのような複雑さがわかりますか？ この記事には、シミュレーションを含む多くのgifが含まれています=）

すぐに数台の車があるこのような部屋を見せてください







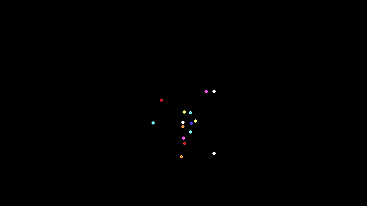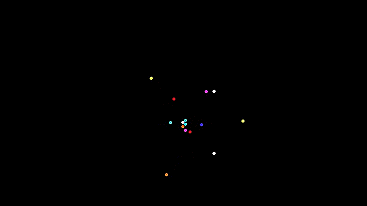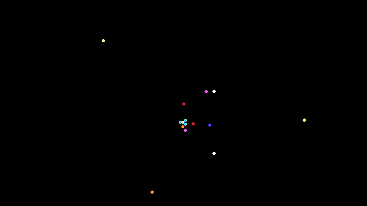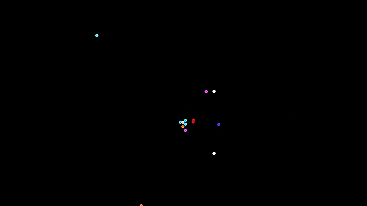
白い円は電球です。 色付き-さまざまな種類の機械。



時々、各オートマトンの軌跡を使用したより美しいデモが得られます。







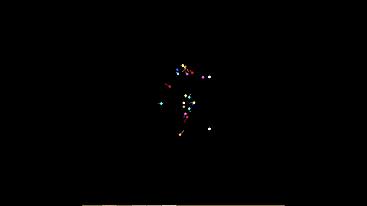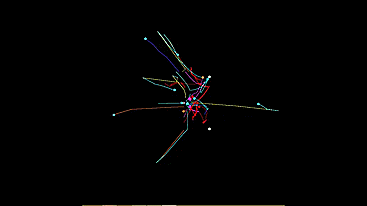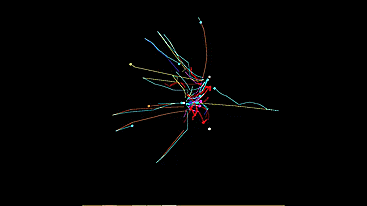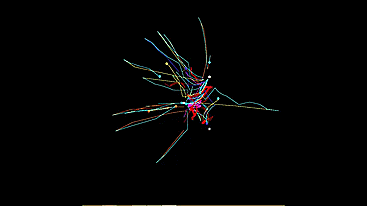
それでは始めましょう。 最初に私は光好性タイプを実現しました。 システム全体をモデル化する必要はありません。 最初は、光源のパワーを距離の2乗で除算し、ベクトル方式で加算し、受信したベクトル「光の方向」を動きベクトルとして機械に転送できるように思えました。 しかし、それはまったく間違っていることが判明しました。



まず、ブライテンベルクシステムでは、マシンに2つの感光要素があります。 指向性センサーとして実装されている場合は前方を向き、無指向性の場合は前方と後方を区別しないでください。 そのため、モーションベクトルに垂直な平面を取り、それが後ろを向いている場合は「光の方向」を反射しました。 その結果、耳は、音がどこから来たのかを区別せず、正面または背面ではなく、右または左のみ、そしてどのような強さかを区別します。



第二に、車輪上の装置は側面に対して垂直に移動できず、最大回転角度（移動距離の単位あたり）、最大速度および慣性を持ちます。 これをすべて追加するには、オートマトンの方向ベクトルに対するモーションベクトルの角度を特定の最大値にトリミングし、それをモジュロでトリミングしてベクトル方式で追加します。V_new= Inertia * V_old +（1-Inertia）* LightDir。





結果：







その結果、特徴が顕著になりました。たとえば、2つの電球のちょうど真ん中を通過する車が動き続けていることがわかります。 すべて順調です。これに基づいて新しいタイプを作成できます。



今、光への恐怖があるでしょう。 これを行うには、すべてを行う必要がありますが、タイプライターの現在の方向に相対する動きベクトルを反映する必要があります（座標に関連する反射ではありません！そうしないと、物理的に非現実的なデバイスが再び表示されます）。









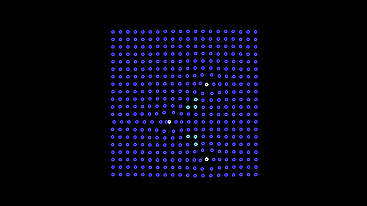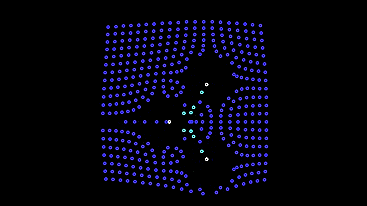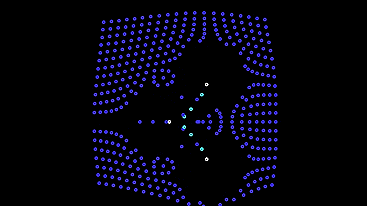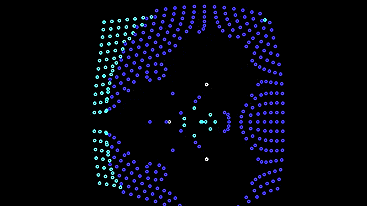
唯一のマイナス-このようなマシンは画面から逃げ出し、空のフィールドを残します。 私たちは彼らに逃げるのを防ぐメカニズムを提供します-暗い場所では電球に戻るまで最初のモデルに振る舞います。



それでは、車にいくつかのニューロードを設定してみましょう。 最初のモデルは、光親和性マシンのモデルを繰り返しますが、ライン上に統合されたニューロードがあります。 センサーからは、ブレーキ信号がニューロンに送られ、ニューロンからは信号がモーターに送られます。 センサーを照らすほど、モーターへの信号が少なくなり、車の速度が遅くなります。 このようなシステムには、最初のモデルとして配線がありますが、2番目のモデルのように動作し、光から逃げます。 しかし、ソースからの距離とともに最初の速度が低下した場合、これは逆になります。加速します。 それに応じて動きベクトルのモジュールを計算するためのコードを修正しましょう：







このタイプライターを初めて作ったとき、それは正しく機能しているように見えましたが、何かが間違っていました...これは、私が何らかの記号を混ぜた最初のバージョンです。







トラックの録音モードで見るのはもっと美しいです-彼らは目のようなものを描きます。







今、次のマシン。 ワイヤーを再度交差させますが、それらにニューロンがあります（コードでは、ベクトルの最後の反射を削除します）。







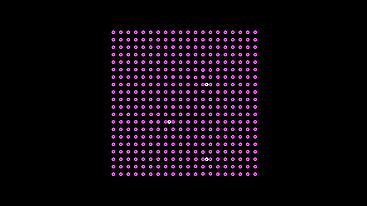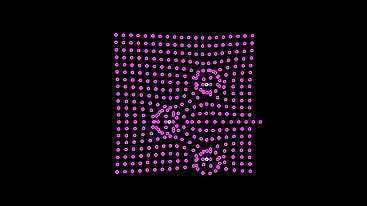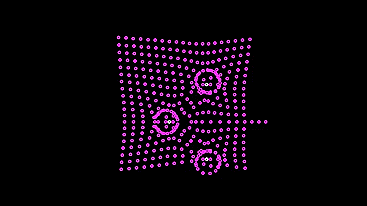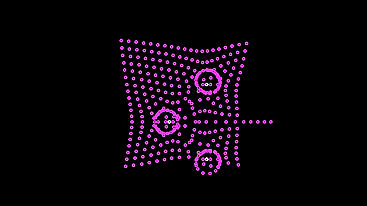
このマシンは賢く、光に壊れず、電球を壊す危険性があります（実際のモデルではそうなります）が、センサーに十分な光が当たると、ブレーキ信号がモーターの信号の生成を完全に停止するように、距離を置いて停止します。



5番目。 ニューロンの複雑なシステムを備えたマシン。 説明については、 この記事を参照できますが、ここでは簡単な方法でこれを行う方法を説明します-光の量によってバリアが追加され、光のレベルがしきい値より高いか低いかに応じて、反射操作の記号が変わります。 実際のマシンは、光がほとんどない場合は3番目として逃げ、多くがある場合は4番目として光に向かう必要があります。 どこかに完全に停止する内側の円もあります-私は長い間係数を拾い、しばしばそれらを変えましたが、「火から世界の端」からの美しい脱出を達成しませんでした。 とにかく、ストップの内側の円は十分に広くする必要があります（面積の半分以上を占める）-これは、距離の増加に伴う光レベルの2次減衰の実装によるものです。







そして最後の1つ 。 これは反対の原則に従ってモデルを変更する必要があります-十分ではないときに光に手を伸ばし、たくさんあるときに逃げる。 Azimovの愛好家は、そのような機械が等電位線（一定レベルの照明の​​線）上で常に円を描くことをすぐに理解します。 そして、これまで使用してきた直接的な「センサーレス」モデルを続行すると、マシンはこのラインに到達して停止します。 現実の世界では、円の中を走るのは、目の一方が円の内側にあり、もう一方が外側にあるという事実によるものであり、内部の神経構造は動きアルゴリズムの新しいケースを作成します-それは光の方向に垂直に動きます。 このタイプのマシンをシミュレートするには、2つのセンサーの実際の説明を追加する必要がありました。そのため、一方のセンサーでは、あるポイントでの照明値がしきい値を下回り、もう一方のセンサーでは、ある距離でセンサーを配置する必要がありました。 センサー間の物理的な距離は視差と呼ばれます（たとえば、人の目、または1つのシステム内の2つの望遠鏡の間）。 これは私の飲んだ後のマシンです（私はねばねばに目を向けませんでした）。











視差の変化は精度の変化につながります











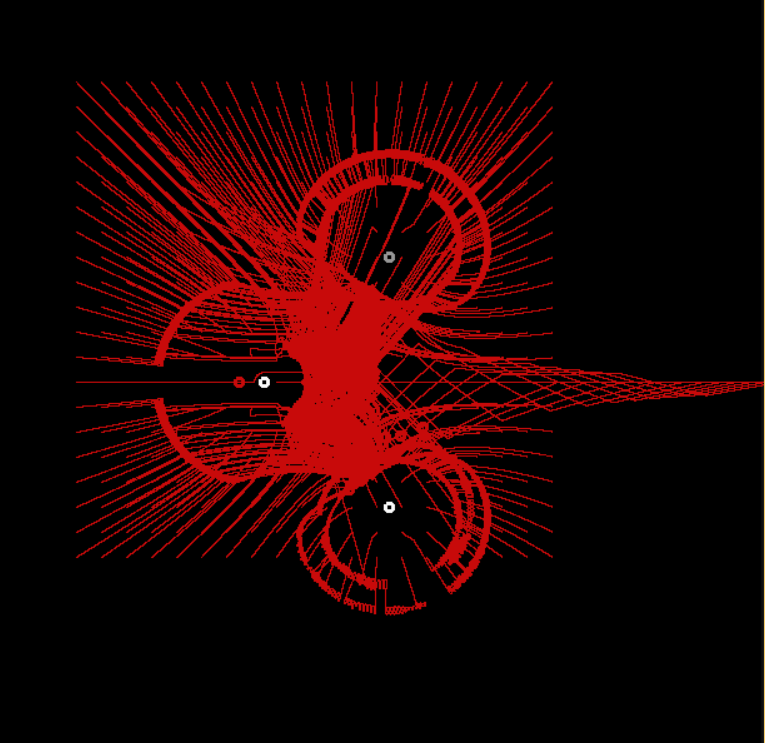
一部の値では、オートマトンはほぼ均等な円弧に沿って移動しますが、他の値では、波状の軌道に沿って移動し、絶えず接近または移動します。 ロボットは線に沿って同様に動作します。



次に、さまざまな種類のマシンのファミリをフィールドにスローします。







記事の冒頭の最初のバージョンは私には少し退屈に思えたので、最初にいくつかのライトを時々消灯させました...そして、 ミキシングアルゴリズムを実行しました 。これは時々マシンのタイプを他のものに変更するため、彼女が「すべての化身」を通過するように：









これらすべてがなければ、1つのフィールドですべてのタイプのグリッドを見ることができます。











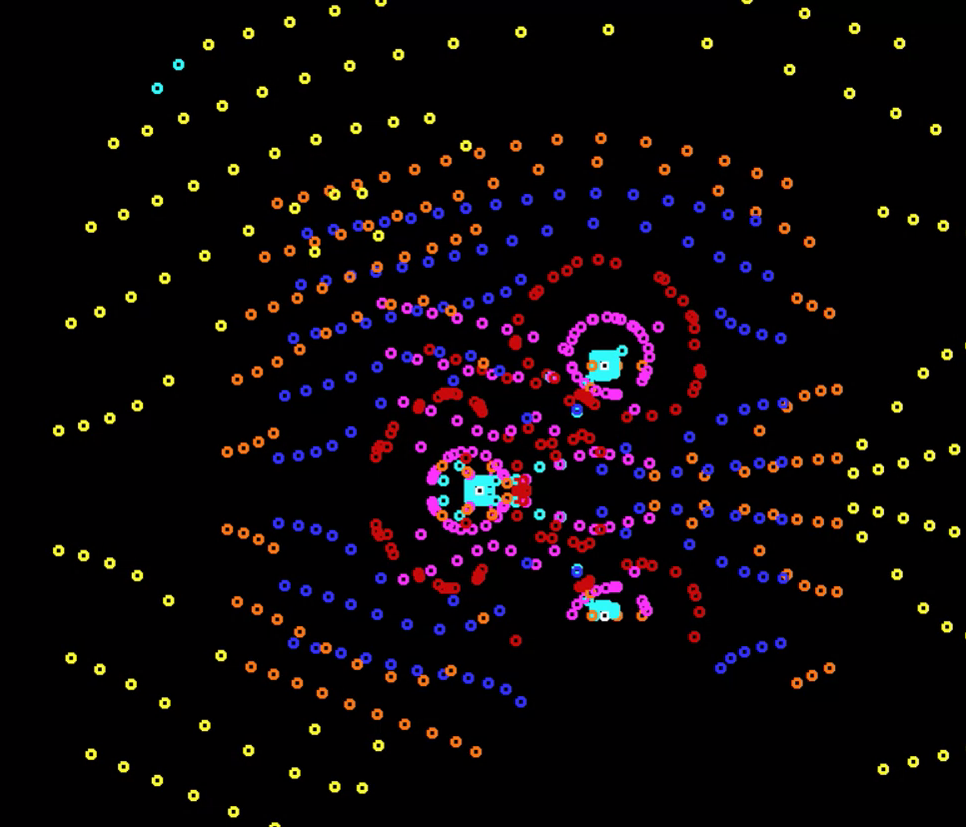
その後、私は車が物理的なサイズを持っているべきだと思ったので（お互いが通り抜けないように）、 衝突を計算することはコンピューター、特に非常に多くの参加者にとって難しいタスクなので、数回撮影してモードをオフにしました









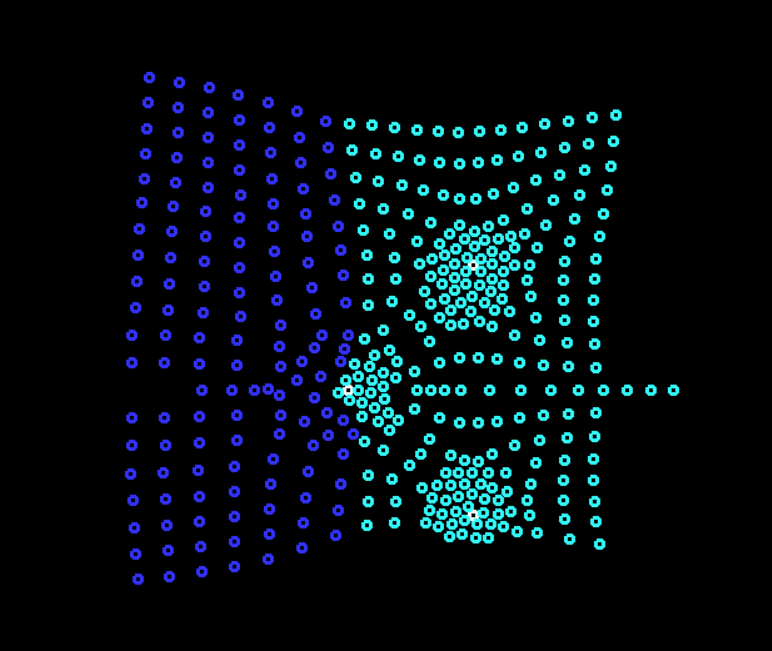
原理的には、すべてが同じで、車だけが漸近的な軌道に沿って押し出され、正確にはそれらに乗っていませんでした。それがすべてです。 衝突せずに世界に戻ります）



遅いシャッタースピードシステムを考えてみましょう-それは何のために努力していますか？

電球の切り替えモードでは、システムを静止画像のままにすることはできませんが、写真家は非常に一生懸命努力しました-彼らはランプに固執し、オフになっている期間中にそれらから逃げる時間がありませんでした。







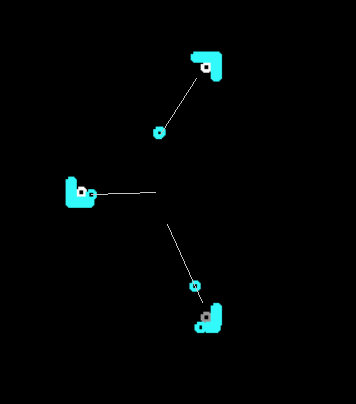
彼らの賢明なバージョンは間に合っており、最終的には3つのランプ間の循環経路に沿って移動する群れがあります。









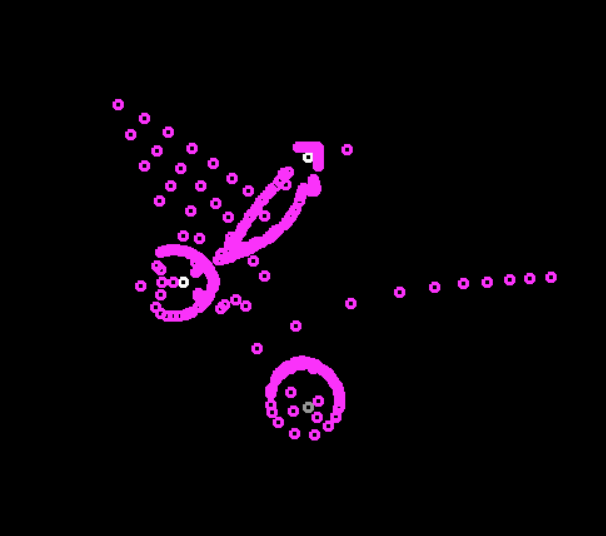
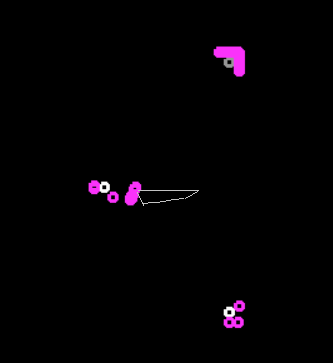
Photo明は異なる働きをします。 保護システムはそれらを除去速度と同じ速度で戻すため、各レベルで均等なノイズが発生し、マシンの約半分がゆっくりと除去され、残りの半分は保護モードで戻ります。







神経細胞によってポンプでくみ上げられたバージョンでは、状況は異なります-すぐに飛び去りますが、ゆっくりと戻ります。 私は彼らが最終的に均一な先細りの円を形成すると予想したが、そうではなかった。 彼らは非対称の形状を保持し、時には美しい写真を与えます







同じカオスに時々似ています：







変化するオートマトンはしばしば同じように振る舞います。 しかし、最終的に、彼らは電球からこれらのレールに沿って電球までかなりの距離を移動する非常に小さなグループに迷い込みます。







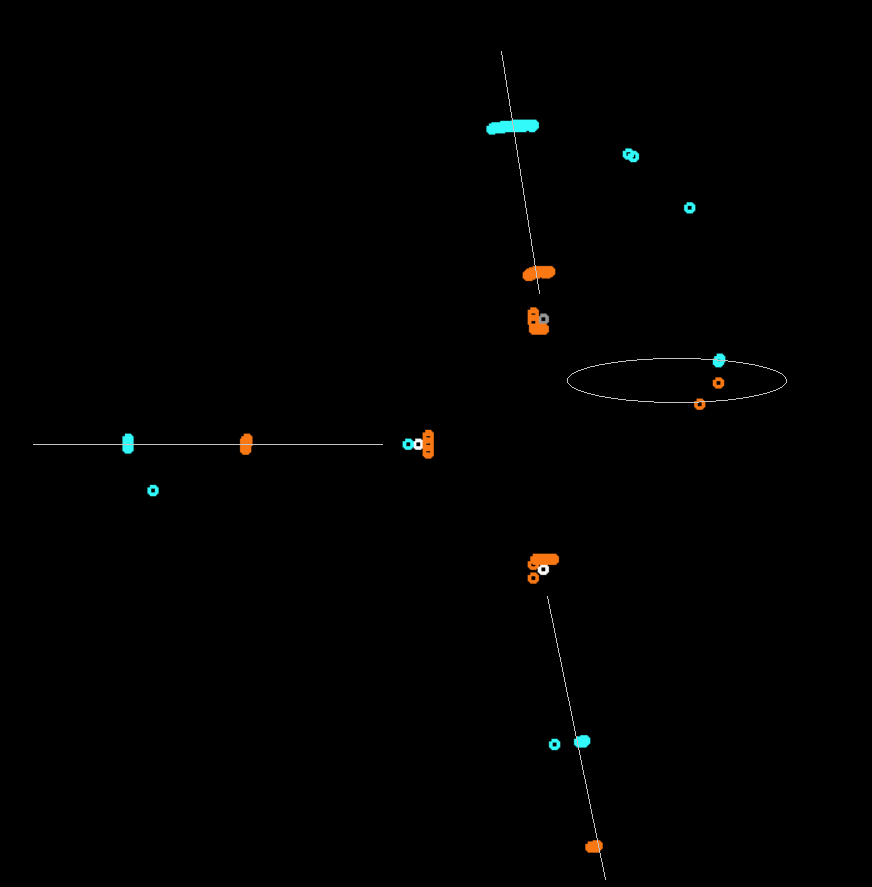
「彼らの波」を捕らえ、部屋の右側で回転するいくつかの機械に加えて。 私は彼らが3つの氏族の1つに加わるのを待ちましたが、これは2時間のシミュレーションの後では発生しませんでした。これは、地球の重力の周りを右から左に飛ぶ小惑星のような、奇妙で動的に安定した軌道の場合と同じようです



ループマシンは、電話の受話器（または笑顔ですか？）を示し、山に積み上げられ、現在動作中のランプに向かって触手を順番に折り畳んだり広げたりし始めました。

丹毒







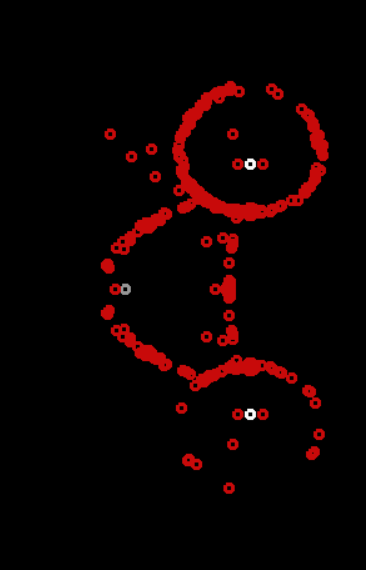
安定モード







それまでの間、長時間のシミュレーションが進行しているため、他のオプションについて考え、さらに3つの非標準タイプを追加しました。 彼らは光ではなく、他の機械に焦点を合わせています。

それらの最初は、マシンが近隣に現れるまで待機し、最も近いものを追いかけようとします。 残りの時間は価値があり悲しいです。







彼らは所有者を必要とするので、それらを犬と呼ぶことができます。 私はそれらをタイプ5でフィールドに配置しました。



別のタイプ-多くのマシンの座標を平均し、群衆にぶつかる-「外向性」。







彼の対po者は、彼の距離を保とうとしている内向的です。







最初は、格子には並進対称性があり、中央のオートマトンには行き先がありません-隣接する方向に近づき、極端なものが散乱するまで待機します。 トラックのモードでは面白そうです-毛皮のようなチップが判明します。







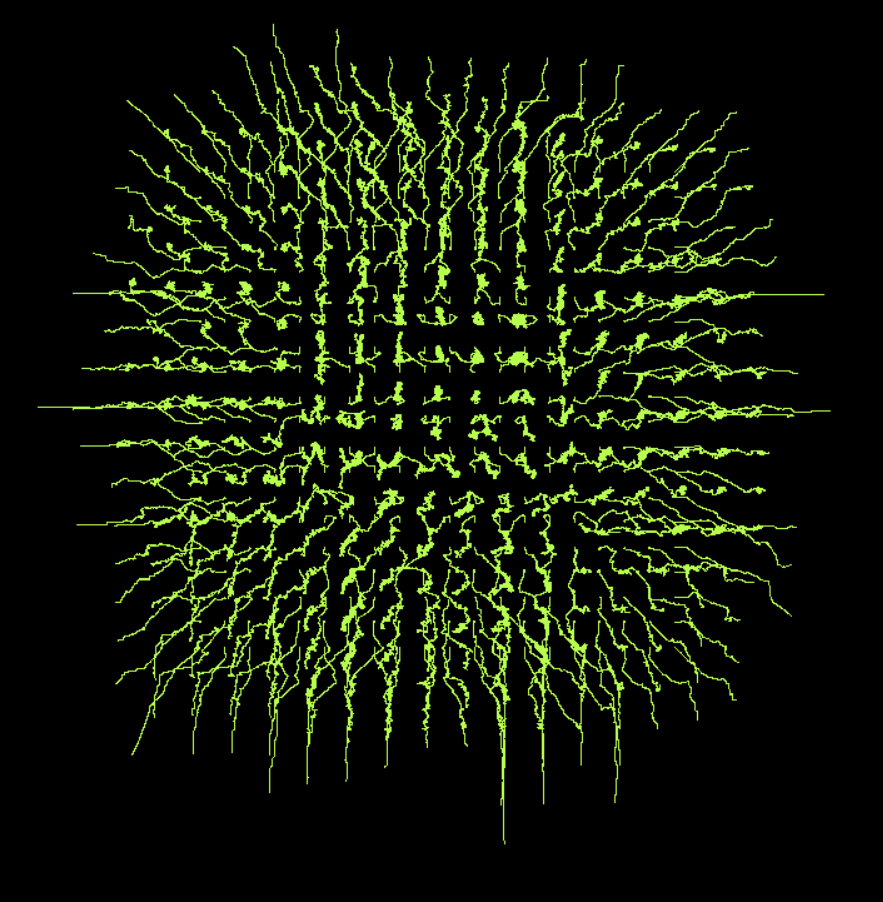
次に、9種類すべて（新しいものを含む）を配置して、グリッドを確認します。 （タイプ混合を含む）







そして、トラックモードでは、彼らはタンポポを描きます











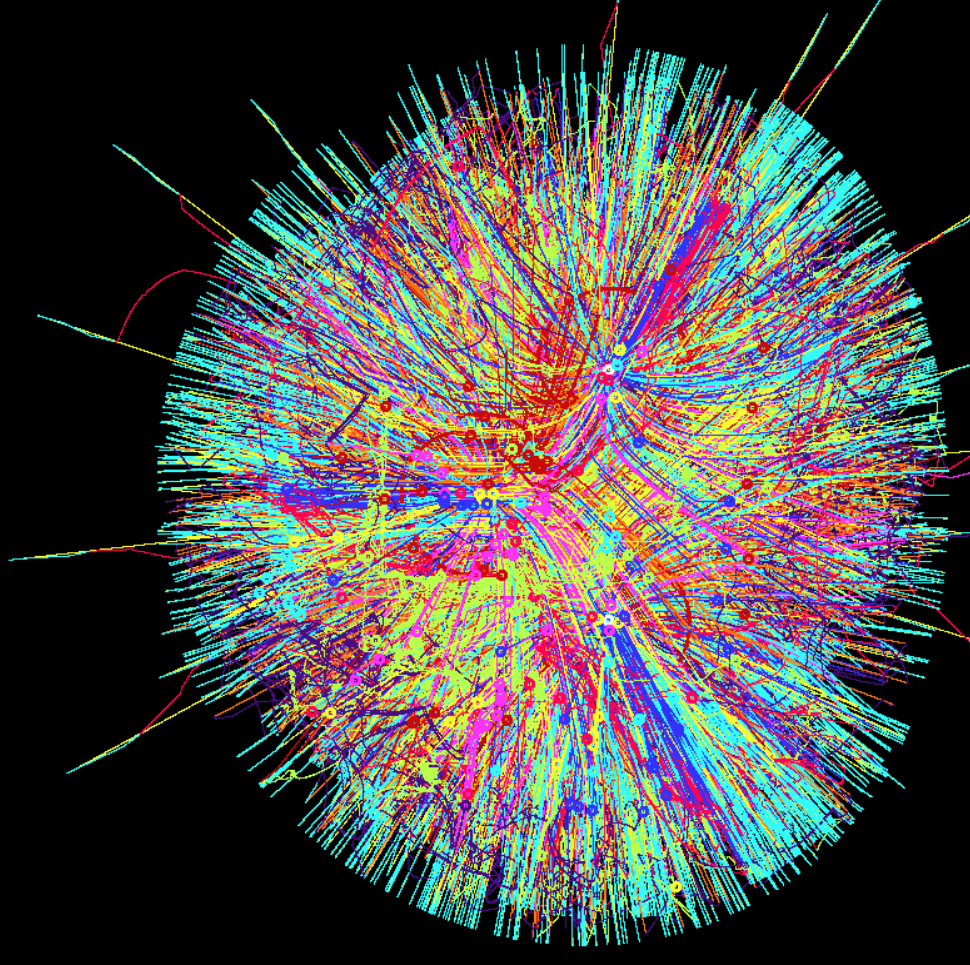
中央に、負のパワー値を持つ光源を配置しました。 私は何を期待していたのかわかりませんが、アンチライトは通常暴走するマシンを引き付けますが、その動作はフォトフォアの「交差」アナログのようにはなりませんが、3番目の、より複雑なものになります。

判明したより多くのタンポポ。













これもタンポポに変わります。 シミュレーションのコーナーで「クモの巣」の絵を見たとき、私は興味を持ちました-逃亡者は次々と光線を去りました、そして、犬はそれらに追いついておらず、凹型の半アーチで一方から他方へ移動しました。 このように大規模に行うと、常に描画されるように、クモの巣を手に入れると思いました。 そのため、私はこの2種類の機関銃のみを部屋に投入しましたが、何かがおかしかったのです。 どのような構成でも、システムは不安定で、犬はある方向に落ちます。その結果、たった1つのタンポポが出てきますが、ウェブはありません。







別のランプを追加しました。









でも...あの...ヤマアラシ？







一般的に、私の好みに関しては、行動は本当に非常に複雑です。 しかし、先に進みましょう。 非線形性を示してみましょう。 スキャッタバージョンはこれに適しています。 球からの発散（これは、照明の中で等電位である電球の周囲の表面）は、決定論的カオスの出現をほぼ保証します。

同じグリッドを非常に小さなサイズで実行してみましょう-車の初期条件が少しだけ異なり（マシンはほぼ1ポイントを残す）、システムがどのように発展し、それが何を示すかを見てみましょう。









同じ小さなグリッドを実行しますが、異なるタイプの車とタイプの混合を有効にします







このような興味深い写真が得られます...変更のために、視覚化モデルを変更できます。たとえば、すべての車を線で接続します（まるで1本の長い糸を引くように）。 そのため、アルゴリズムが最初の滑らかなマシングリッドをどのように正確に破壊し、さまざまな部分をどこに送信するか、つまり世界中でどのように移行するかを見る方が便利です。







メディアプレーヤーのような粘着性のものが判明します。

時々面白い数字が表示されます。















一般的に 、そのようなシミュレータ。 コメントであなたのアイデアや提案を提案したり、他にどんなものを追加したり、どんな実験をしたりしてください。 個人的には、結果として得られるものは、非線形システムの理論の便利なデモンストレーションだと思います-その中で、単純なシステムの複雑さを示す漸近、分岐、好奇心の強いパターンを探すことができます...一般的に-カラー写真を参照してください。



みんな、ロボット心理学者に良い。 以上です。