🤱🏿 🤠 💽 間隔インデックスについて 👨‍⚖️ 🙎🏻 💅🏻

カットの下で、間隔のインデックス付けに特別なインデックスが必要かどうか、多次元の間隔を処理する方法、2次元の長方形を4次元の点のように扱うことができるのは本当かなどを理解します。これはすべてPostgreSQLの例です。

トピックの開発中（ 1、2、3、4、5、6、7 ）。

データは値ではなく、信頼区間などで表示される場合があります。または、これらは本当に値の範囲です。繰り返しますが、長方形も間隔ですが、1次元ではありません。対数時間で、目的の間隔と交差する間隔がデータにあるかどうかを確認することはできますか？

はい、もちろんです。たとえば、グレイコードなどに基づいてブロック値を計算し、インデックスを作成するための独創的なスキーム（さらに細かいフィルタリングを使用）を思いつくことがあります。この場合、精度が失われた間隔は特定の（インデックス付き）数値にエンコードされます;検索時に、間隔はチェックする必要がある値（サブ間隔）のセットを生成します。このセットは対数によって制限されます。

ただし、GiST は Rツリーを使用して時間間隔（tsrange）のインデックスを作成できます。

create table reservations(during tsrange); insert into reservations(during) values ('[2016-12-30, 2017-01-09)'), ('[2017-02-23, 2017-02-27)'), ('[2017-04-29, 2017-05-02)'); create index on reservations using gist(during); select * from reservations where during && '[2017-01-01, 2017-04-01)';

もちろん、著者は、多次元インデックスを愛する~~Rツリーに対する十字軍で~~ 、そのようなトピックを通り抜けることはできませんでした。

では、Rツリーはどのように間隔を処理しますか？他の空間オブジェクトと同様に。間隔は1次元の長方形です;ページを分割するとき、Rツリーは子孫ページ内の分散を最小化し、ページ間の最大化を試みます。

間隔をポイントに変えることは可能ですか？たとえば、開始をXとし、終了をYとして考えると、結局のところ、2次元のポイントとして2つの数値を使用することを誰が禁止できるのでしょうか。しかし、そのようなデータには内部依存性があります。データのセマンティクスは、検索クエリのセマンティクスと結果の解釈につながります。

状況を把握する最も簡単な方法は、目で見ることです。

0から10,000までのサイズの範囲で、0から100,000までの間隔の始まりで100個のランダムな間隔があります

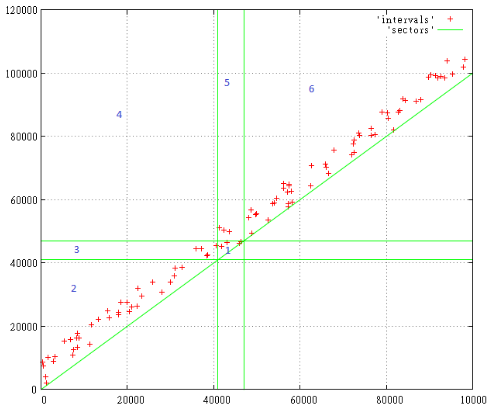
図1

検索クエリは[41,000 ... 47,000]であり、特定の範囲と交差するすべての間隔に関心があります。

数字は、発生する検索ゾーンを示しています。明らかな理由で対角線の下にあるものはすべて存在しません。

したがって、ゾーンごとに：

これには、厳密に検索クエリ内にある間隔が含まれます
ここで、必要な間隔の前に開始および終了したすべてのもの
これらの間隔は、検索クエリの前に開始し、終了しました
ここに検索を完全にカバーする間隔があります
これらの間隔は、開始中に開始されましたが、要求後に終了しました
ここで彼の後に始まり、終わったすべてのもの

したがって、すべての交差点を検索するには、クエリを[0 ... 47 000、41 000 ... 100 000]に展開する必要があります。ゾーン1、3、4、5を含める必要があります。

リクエストがレイヤー全体の4分の1のサイズになったという事実は、対角線に沿った狭いストリップのみが読み込まれるため、怖いものではありません。はい、レイヤー全体のサイズに大きな間隔があるかもしれませんが、比較的少数です。

もちろん、大きなオブジェクトはパフォーマンスに影響しますが、実際には存在し、ほとんどすべての要求の発行に該当するため、何もできません。「パスタモンスター」のインデックスを作成しようとすると、インデックスは実際に機能しなくなります。テーブルを表示して余分なものを除外する方が安価です。

しかし、どうやら、どのようなインデックス付け方法でも、そのようなデータには問題があります。

このアプローチには他の欠点がありますか？データは何らかの方法で「縮退」しているため、おそらくRツリーのページを分割するヒューリスティックの効率は低下します。しかし、最大の不便は、間隔を処理し、検索クエリを正しく設定していることを常に念頭に置いておく必要があることです。

ただし、これはすでにRツリーではなく、空間インデックスに適用されます。前に使用したZ曲線（ZオーダーBツリー上に構築）を含みます。データの縮退はZカーブにとって重要ではありません。これらは自然な順序の単なる数値であるためです。

とりわけ、Z曲線はRツリーよりもコンパクトです。そのため、指定エリアでの見通しを明確にしていきます。

たとえば、 X座標がセグメントの始まりであり、Yがその終わりであることを受け入れました。 しかし、反対の場合はどうなりますか？ Rツリーは、Zカーブの場合、どちらもほとんど変化しません。クロールの構成は異なりますが、読み取られるページの平均数は同じです。

軸の1つでデータをミラーリングするのはどうですか 。最後に、Z曲線（Yにミラーリングされている）があるので、データを文字Zの斜めクロスバーに配置します。それでは、数値実験を行いましょう。

1,000のランダムな間隔を取り、Z値に応じて10ページに分割します。すなわち並べ替えて100個で割ると、得られたものが表示されます。 X、Y、最大（X）-X、Yの2セットを準備します

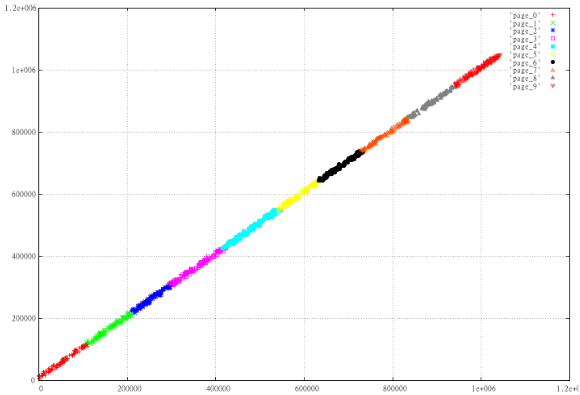
図2通常のZ曲線

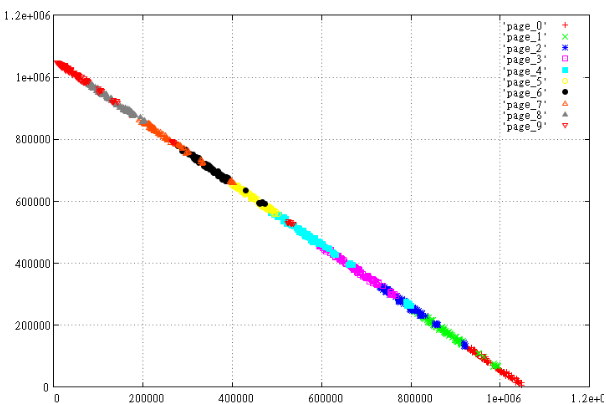
図3ミラーリングされたデータ。

表示されたデータがどの程度「悪い」か、ページが互いにクロールするかどうか、ページの周囲がはるかに大きいかどうかを明確に見ることができます。

なぜこれが起こったのですか？この場合、理由は表面にあります。 2次元の長方形の場合、左下隅のZ値は右上よりも<=です。したがって、ほぼ線形のデータをページに慎重に切り分ける理想的な方法は、それらを直線X = Yに沿って配置することです。

また、範囲の先頭から末尾ではなく、中心の長さをインデックス化する場合は ？この場合、図2を時計回りに45度回転したかのように、データはX軸に沿って伸びます。問題は、同時に検索領域も45度回転し、単一のクエリで検索することができなくなることです。

この方法で複数のディメンションを持つ間隔にインデックスを付けることは可能ですか？もちろん。 2次元の長方形は4次元の点に変わります。主なことは、どの座標に置くかを忘れないことです。

間隔を非間隔値と混在させることは可能ですか？はい、Z曲線検索アルゴリズムは値のセマンティクスを知らないため、フェースレス数で動作します。このセマンティクスに従って検索範囲が設定され、結果の解釈がそれに基づいている場合、問題は発生しません。

数値実験

「パスタモンスター」に近い条件でZカーブのパフォーマンスを確認してみましょう。データモデルは次のとおりです。

8次元インデックス、パフォーマンスとパフォーマンスは既にテスト済みです
いつものように、1億ポイント
オブジェクト-3次元平行六面体-6次元を占める
時間間隔に残りの2つの次元を与えます
100個の平行六面体-X＆Yラティス10X10を形成します
各ボックスは1時間単位で使用されます
時間単位ごとに、平行六面体は高さ0から開始してZで10単位増加します

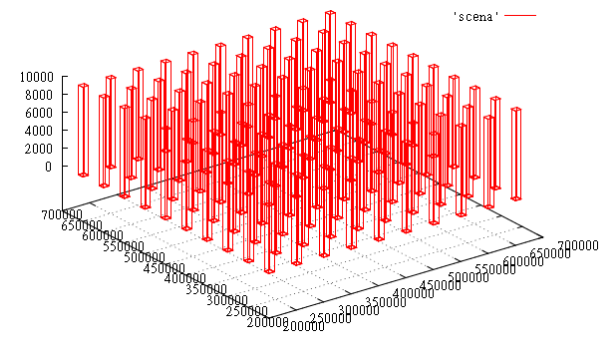
図4時間T = 1000でのデータのスライス

このテストでは、検索パフォーマンスに影響するため、拡張オブジェクトのインデックス作成をテストします。

8次元テーブルを作成し、データとインデックスを入力します

 create table test_points_8d (p integer[8]); COPY test_points_8d from '/home/.../data.csv'; create index zcurve_test_points_8d on test_points_8d (zcurve_num_from_8coords (p[1], p[2], p[3], p[4], p[5], p[6], p[7], p[8]));

主な順序：xmax、xmin、ymax、ymin、zmax、zmin、tmax、tmin

データファイル（data.csv）：

 {210000,200000,210000,200000,0,0,0,0} {210000,200000,210000,200000,10,0,1,1} {210000,200000,210000,200000,20,0,2,2} {210000,200000,210000,200000,30,0,3,3} {210000,200000,210000,200000,40,0,4,4} {210000,200000,210000,200000,50,0,5,5} {210000,200000,210000,200000,60,0,6,6} {210000,200000,210000,200000,70,0,7,7} {210000,200000,210000,200000,80,0,8,8} {210000,200000,210000,200000,90,0,9,9} ...

テスト要求[200,000 ... 300,000; 200,000 ... 300,000; 100 ... 1000; 10 ... 11]：

 select c, t_row from (select c, (select p from test_points_8d t where c = t.ctid) t_row from zcurve_8d_lookup_tidonly('zcurve_test_points_8d', 200000,0,200000,0,100,0,10,0, 1000000,300000,1000000,300000,1000000,1000,1000000,11 ) as c) x;

答えは：

  c | t_row -------------+------------------------------------------- (0,11) | {210000,200000,210000,200000,100,0,10,10} (0,12) | {210000,200000,210000,200000,110,0,11,11} (103092,87) | {260000,250000,210000,200000,100,0,10,10} (103092,88) | {260000,250000,210000,200000,110,0,11,11} (10309,38) | {210000,200000,260000,250000,100,0,10,10} (10309,39) | {210000,200000,260000,250000,110,0,11,11} (113402,17) | {260000,250000,260000,250000,100,0,10,10} (113402,18) | {260000,250000,260000,250000,110,0,11,11} (206185,66) | {310000,300000,210000,200000,100,0,10,10} (206185,67) | {310000,300000,210000,200000,110,0,11,11} (216494,93) | {310000,300000,260000,250000,100,0,10,10} (216494,94) | {310000,300000,260000,250000,110,0,11,11} (20618,65) | {210000,200000,310000,300000,100,0,10,10} (20618,66) | {210000,200000,310000,300000,110,0,11,11} (123711,44) | {260000,250000,310000,300000,100,0,10,10} (123711,45) | {260000,250000,310000,300000,110,0,11,11} (226804,23) | {310000,300000,310000,300000,100,0,10,10} (226804,24) | {310000,300000,310000,300000,110,0,11,11} (18 rows)

このようなデータモデルが優れている理由は、結果の正確性を簡単に評価できるためです。

新たに発生したサーバーで、EXPLAIN（ANALYZE、BUFFERS）を介した同じリクエスト

表示： 501ページが読み取られた。

さて、インデックスを移動しましょう。しかし、xmin、ymin、zmin、xmax、ymax、zmax、tmin、tmaxというキーの順序でインデックスの同じクエリを見るとどうなりますか。起動には531の読み取りが表示されます。多すぎる。

さて、幾何学的な偏りを排除しましょう。今度は、列が10ずつではなく、サイクルごとに1単位ずつ成長するようにします。リクエスト（キー：xmax、xmin、ymax、ymin、zmax、zmin、tmax、tmin）

 EXPLAIN (ANALYZE,BUFFERS) select c, t_row from (select c, (select p from test_points_8d t where c = t.ctid) t_row from zcurve_8d_lookup_tidonly('zcurve_test_points_8d', 200000,0,200000,0,0,0,10,0, 1000000,300000,1000000,300000,1000000,1000,1000000,11) as c) x;

156ページが読まれたと言います！

さて、少し統計を見てみましょう。10,000の一連のランダムリクエストで、さまざまな種類のキーのキャッシュ内の読み取り/ヒットの平均数を見てみましょう。

サイズ100 000X100 000X100 000X10

キーの順序が

（xmin、1,000,000-xmax、ymin、1,000,000-ymax、zmin、1,000,000-zmax、tmin、1,000,000-tmax）

読み取りの平均数は21.8217で、キャッシュ内のヒットは2437.51です。

同時に、問題のオブジェクトの平均数は17.81です。

キーの順序が（xmax、xmin、ymax、ymin、zmax、zmin、tmax、tmin）の場合

読み取りの平均数は14.2434で、キャッシュ内のヒットは1057.19です。

同時に、問題のオブジェクトの平均数は17.81です。

キーの順序が（xmin、xmax、ymin、ymax、zmin、zmax、tmin、tmax）の場合

読み取りの平均数は14.0774、キャッシュ内のヒットは1053.22です。

同時に、問題のオブジェクトの平均数は17.81です。

ご覧のとおり、この場合のページキャッシュは非常に効率的に機能します。その数の測定値はすでに受け入れられます。

そして最後に、Zカーブアルゴリズムが8次元空間にどのように対処するかを、好奇心から目で見てみましょう。

以下は、クエリ解析の範囲の予測です-

[200,000 ... 300,000; 200,000 ... 300,000; 0 ... 700 001; 700 000 ... 700 001]。

合計18の結果、1687のサブクエリ。生成されたサブクエリが表示されます。緑色の十字-Bツリーの測定値、青色の十字-見つかった結果。

各十字の下には、いくつかのマークがあります。 700,000と700 001のように、近くのマークがマージされます。

5 X軸

6 Y軸

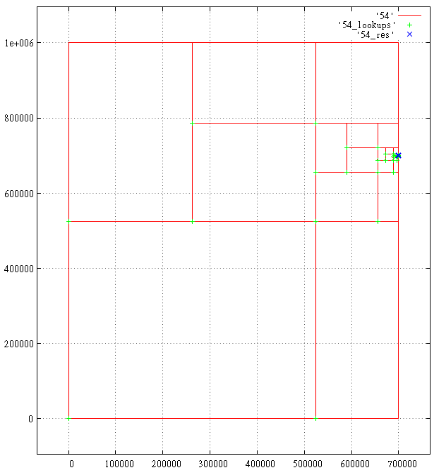
図7 Z軸

図8時間

間隔インデックスについて

数値実験

More articles: