🐵 👐🏻 👨🏽‍🌾 数学探偵：方程式の正の整数解を見つける 👨‍👩‍👦‍👦 👩‍👧‍👧 🆖

「私は、アンドリューとリチャード・ガイによる以前の作品のスタイルでキューブ表現タスクを試しました。数値結果は驚くべきものでした...」（MathOverflowについてのコメント）

これが、数年前に引退した数学者アラン・マクラウドがこの方程式に出会った方法です。そしてそれは本当にとても興味深いです。正直なところ、これは私が今まで見た中で最高のディオファントス方程式の一つですが、私はそれらの多くを見たことはありません。

それは、誰かの冷酷な心（スリダール、それはあなただった？）によって発明されたオタクのネットにひったくる疑似画像として広まり始めたときに見つけた。私はすぐにそれが何であるかを理解しませんでした。写真は次のようになりました。

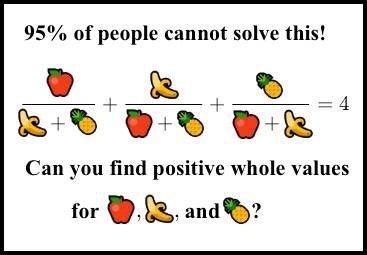
「95％の人がこの謎を解かないでしょう。 正の整数値を見つけることができますか？」

おそらく、似たようなミーム写真を見たことがあるでしょう。これは常に純粋なゴミです。クリックの餌：「MITの卒業生の95％は解決しません！」「彼女」は、ある種のばかげた、または不十分に定式化されたタスク、または脳のための些細なトレーニングです。

しかし、この写真は完全に異なっています。このミームは、スマートまたは悪のジョークです。約99.999995％の人々は、数論に関与していない主要な大学の数学者のかなりの部分を含めて、それを解決するわずかな機会を持ちません。はい、解決可能ですが、本当に複雑です。（ちなみに、スリダールはそれを発明しなかった、というか、彼は完全に発明しなかった。このコメントの話を参照）。

他に何も役に立たない場合は、コンピューターにそれを解決させることができると思うかもしれません。この一見単純な方程式の解を見つけるためのコンピュータープログラムを書くのは非常に簡単です。もちろん、コンピューターは遅かれ早かれそれらを見つけます（存在する場合）。 大きな間違い 。ここでは、単純なコンピューターのブルートフォースメソッドは役に立ちません。

誰もが楕円曲線に必要なすべてをすでに知っていることを受け入れないと、完全なソリューションを記事に組み込むことが可能かどうかはわかりません。ここでは、簡単な概要のみを説明します。主な参考資料は、2014年にAnnales Mathematicae et Informaticaeで公開された、BremnerとMacLeodの「異常な立方体表現の問題」という題名の比較的最近の素晴らしい作品です。

それでは始めましょう。

方程式の正の整数解を探しています

f r a c a b + c + f r a c b a + c + f r a c c a + b = 4 t a g 1

$\ frac {a} {b + c} + \ frac {b} {a + c} + \ frac {c} {a + b} = 4 \ tag 1$

（変数の表記を作業で使用されている表記に置き換えました）。

方程式を調べるときに最初に行うことは、正しいコンテキストに置くことです。質問をしなければなりません：この方程式は何ですか？したがって、整数解を見つけるように求められます。つまり、それは数論の問題です。現在の定式化では、方程式は有理関数（他の多項式で割り切れる多項式）を使用していますが、分母の公倍数で乗算して方程式をクリーンアップし、多項式のみを取得する、つまりディオファントス方程式の形式にすることができることは明らかです。「陽性」の要件はかなり珍しいものであり、これから見るように、すべてを複雑にします。

では、ここにはいくつの変数がありますか？質問はばかげているようです：明らかに、3、すなわち

a

$a$ 、

b

$b$ そして

c

$c$ 。しかし、時間をかけてください。経験豊富な数論研究者は、方程式が同質であることをすぐに気付くでしょう。これは、

（ a 、 b 、 c ）

$（a、b、c）$ は方程式の解の1つであり、解は

（ 7 a 、 7 b 、 7 c ）

$（7a、7b、7c）$ 。理由はわかりますか？各変数に定数（

7

$7$ -これは単なる例です）、各部分の定数が削減されるため、何も変更しません。

f r a c t a t b + t c = f r a c t a t （ b + c ） = f r a c a b + c

$\ frac {ta} {tb + tc} = \ frac {ta} {t（b + c）} = \ frac {a} {b + c}$

これは、方程式が3次元になりすますことを意味します。実際、2次元です。幾何学的表現では、表面があります（一般に、3つの変数を持つ1つの方程式が2次元の表面を定義します。一般に、

k

$k$ との方程式

n

$n$ 変数を設定する

d

$d$ 次元多様体、ここで

d = n - k

$d = n-k$ ）しかし、この表面は実際には、振動して原点を通過する線によって制限されています。結果のサーフェスは、ユニットプレーンをどのように切断するかを理解することで理解できます。これは射影曲線です。

この情報を計算する最も簡単な方法は次のとおりです。

c = 0

$c = 0$ 、およびその対象

c n e q 0

$c \ neq 0$ 。最初のケースでは、2つの変数しか残っていません。

a

$a$ そして

b

$b$ 、そして2番目では単純に除算できます

c

$c$ 解決策を得る

c = 1

$c = 1$ 。したがって、 合理的な解決策を単純に探すことができます

a

$a$ そして

b

$b$ ケース用

c = 1

$c = 1$ 、それらに共通因子を掛けて、

a

$a$ 、

b

$b$ そして

c

$c$ 。本質的に、同次方程式の整数解は、不均質バージョンの有理解に対応し、これは1次元分少なくなります。

続き：方程式の程度は？方程式の次数は、単項式の方程式に現れるすべての最大次数です。「単項式」は、「次数」が複数の単項式の数であるいくつかの変数の積です。例えば

a^{2} b c^{4}

$a ^ 2bc ^ 4$ 度の単項式になります

$inline$ 。

ディオファントス方程式の振る舞いは、その次数に強く依存します。一般的に：

学位あり $1$ すべてがシンプルです。
程度 $2$ 完全に分析され、かなり基本的な方法で解決できます。
程度 $3$ -これは深層理論の広大な海であり、100万の未解決の問題です。
程度 $4$ 以上...非常に複雑です。

学位があります

3

$3$ 。なんで？単に除算器で乗算します。

a （ a + b ） （ a + c ） + b （ b + a ） （ b + c ） + c （ c + a ） （ c + b ） = 4 （ a + b ） （ a + c ） （ b + c ）

$a（a + b）（a + c）+ b（b + a）（b + c）+ c（c + a）（c + b）= 4（a + b）（a + c）（b + c）$

ブラケットを開かなくても、次の程度であることがわかります。

3

$3$ ：一度に3つ以上の変数を乗算することはありません。次のような部品を入手します

a^{3}

$a ^ 3$ 、

b^{2} c

$b ^ 2c$ そして

a b c

$abc$ 、しかし、3つの要因以上のものはありません。変換を実行すると、方程式は次の形式になります

a^{3} + b^{3} + c^{3} - 3 （ a^{2} b + a b^{2} + a^{2} c + a c^{2} + b^{2} c + b c^{2} ） - 5 a b c = 0

$a ^ 3 + b ^ 3 + c ^ 3-3（a ^ 2b + ab ^ 2 + a ^ 2c + ac ^ 2 + b ^ 2c + bc ^ 2）-5abc = 0$

除数の一部が等しい場合、除数による乗算は不可能であると主張するかもしれません

0

$0$ 。これは事実です-実際、新しい方程式には元の方程式に対応しないいくつかの解があります。しかし、実際には良いことです。多項式を使用したバージョンでは、オリジナルにいくつかの「パッチ」が追加され、作業が簡単になります。元の除数が具体的な決定ごとに消えないかどうかを確認するだけです。

実際、多項式を含む方程式は簡単に解くことができます。たとえば、

a = - 1

$a = -1$ 、

b = 1

$b = 1$ 、

c = 0

$c = 0$ 。これは良いことです。合理的な解決策があります（合理的なポイント）。これは、3次方程式（次数= 3）が実際に楕円曲線であることを意味します。

方程式が楕円曲線であることがわかったら、a）満足し、b）絶望します。まだ学ぶべきことがたくさんあります。この方程式は、非常に複雑な解を見つけるために、楕円曲線の強力な理論をどのように適用できるかの良い例です。

楕円曲線が通常作成される最初のことは、それをワイエルシュトラス形にすることです。これは次のような方程式です

y^{2} = x^{3} + a x + b

$y ^ 2 = x ^ 3 + ax + b$

そして時々どのように

y^{2} = x^{3} + a x^{2} + b x + c

$y ^ 2 = x ^ 3 + ax ^ 2 + bx + c$

（これは拡張されたWeierstrassフォームと呼ばれます。オプションですが、時にはより便利です）。

通常、楕円曲線はこの形式に縮小できます（特性が小さいフィールドで作業している場合を除きますが、ここではそれらについて心配する必要はありません）。適切な変換を見つける方法を説明するには長すぎるので、これは絶対に機械的なプロセスであることを知ってください（少なくとも1つの合理的なポイントがあることが重要です）。あなたのためにすべてを行う計算代数のさまざまなパッケージがあります。

しかし、あなたが知らなくても。変換を見つける方法は、チェックするのが非常に簡単です。少なくとも純粋に機械的に行われます。私たちの場合に必要な変換は、恐ろしく見える式によって与えられます

x = f r a c - 28 （ a + b + 2 c ） 6 a + 6 b - c

$x = \ frac {-28（a + b + 2c）} {6a + 6b-c}$

y = f r a c 364 （ a - b ） 6 a + 6 b - c

$y = \ frac {364（a-b）} {6a + 6b-c}$

どこから来たブードゥー教の魔法のように見えることは知っていますが、信じられませんが、そうではありません。これらの変換を、単調ではなく、単純な代数計算を使用して取得したので、

y^{2} = x^{3} + 109 x^{2} + 224 x \タ グ 2

$y ^ 2 = x ^ 3 + 109x ^ 2 + 224x \タグ2$

この式は完全に異なって見えますが、実際には元の信頼できるモデルです。グラフィカルに、それはこのように見えます-2つの実部を持つ典型的な楕円曲線：

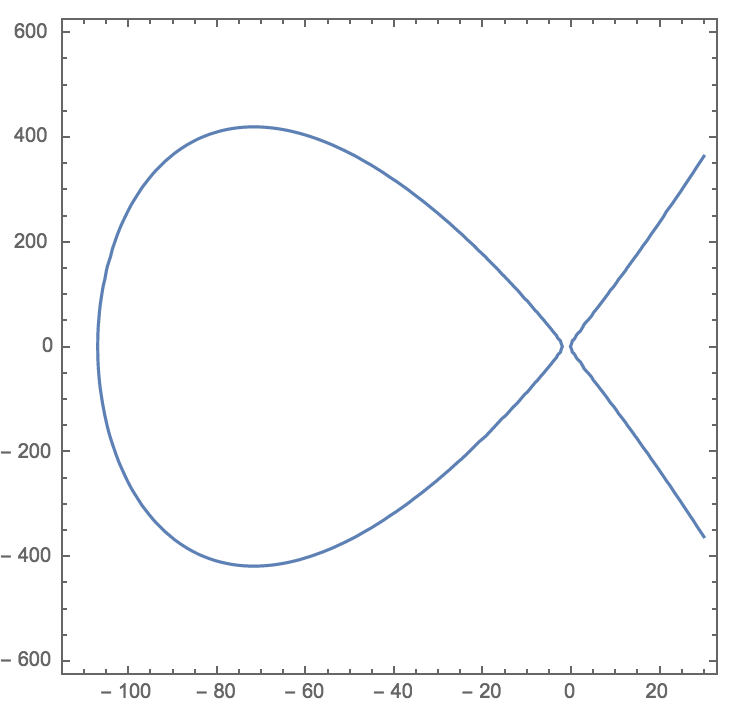
右側の「フィッシュテール」は「無限に、そしてその先まで」成長します。左側の楕円形は閉じており、非常に興味深いものです。

解決策がある

（ x 、 y ）

$（x、y）$ この方程式の、必要な値を復元できます

a

$a$ 、

b

$b$ 、

c

$c$ 方程式を使用して

a = f r a c 56 - x + y 56 - 14 x

$a = \ frac {56-x + y} {56-14x}$

b = f r a c 56 - x - y 56 - 14 x

$b = \ frac {56-x-y} {56-14x}$

c = f r a c - 28 - 6 x 28 - 7 x

$c = \ frac {-28-6x} {28-7x}$

（そのトリプレットを覚えておいてください

（ a ： b ： c ）

$（a：b：c）$ 射影する必要があります-これらの方程式を使用して取得する値に関係なく、常に定数を掛けることができます）。

次の2つのディスプレイは、

a

$a$ 、

b

$b$ 、

c

$c$ で

x

$x$ 、

y

$y$ また、逆の場合、これら2つの方程式は、数論の観点から「同じ」であることを示しています。一方の合理的な解は、他方の合理的な解を与えます。技術的には、これは双有理同値と呼ばれ、代数幾何学の基本概念です。すでに気づいたように、正しく表示されない例外ポイントが存在する場合があります。これらは次の場合です

a + b

$a + b$ 、

a + c

$a + c$ または

b + c

$b + c$ 等しい

0

$0$ 。これは、双合理的等価の場合の通常の報復であり、不安を引き起こすべきではありません。

例を見てみましょう。

楕円曲線上に適切な有理点があります（2）：

x = - 100

$x = -100$ 、

y = 260

$y = 260$ 。見つけるのはそれほど簡単ではないかもしれませんが、確認するのは非常に簡単です。これらの値を挿入するだけで、2つの半分が同じであることがわかります（この点をランダムに選択しませんでしたが、これまでは重要ではありません）。単純にどの値を確認することができます

a

$a$ 、

b

$b$ 、

c

$c$ 彼女は私たちを与えます。取得します

a = 2 / 7

$a = 2/7$ 、

b = - 1 / 14

$b = -1 / 14$ 、

c = 11 / 14

$c = 11/14$ 、そして共通因子を掛けることができるので、結果は次のように変換されます

a = 4

$a = 4$ 、

b = - 1

$b = -1$ 、

c = 11

$c = 11$ 。

そして確かに

f r a c 4 - 1 + 11 + f r a c - 1 4 + 11 + f r a c 11 4 - 1 = 4

$\ frac {4} {-1 + 11} + \ frac {-1} {4 + 11} + \ frac {11} {4-1} = 4$

簡単に見ることができます。これは、整数の元の方程式に対する単純な解決策ですが、残念ながら、正の整数ではありません。この決定は、手作業で行うのは容易ではありませんが、ここで説明した巨像をすべて使用せずに、少しの忍耐で行うことも簡単です。最も難しいことは、肯定的な決定です。

ここで、たとえば、楕円曲線上の有理点を受け取った場合、

P = （ - 100, 260 ）

$P =（-100,260）$ 曲線（2）では、Quoraの前の記事で説明したコードとタンジェントの手法を使用して他の生成を開始できます。

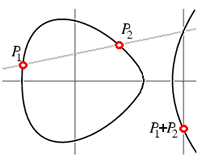
まず、ポイントを追加します

P

$P$ 自分自身に、ポイントで曲線の接線を見つける

P

$P$ そして、彼女が再び曲線に出会う場所を決定します。結果は少し威圧的です：

P + P = 2 P = （ 8836 / 25 、 - 950716 / 125 ）

$P + P = 2P =（8836/25、-950716/125）$

また、この新しいポイントは値に対応します

a

$a$ 、

b

$b$ 、

c

$c$ 元の方程式の解である

（ a 、 b 、 c ） = （ 9499 、 - 8784 、 5165 ）

$（a、b、c）=（9499、-8784、5165）$

このソリューションは、手動で見つけるのは簡単ではありませんが、それでもコンピューターの能力の範囲内です。しかし、それはまだポジティブではありません。

失敗を恐れずに、計算を続けます

3 P = 2 P + P

$3P = 2P + P$ 直線を結ぶことで決定できます

P

$P$ そして

2 P

$2P$ 曲線との3番目の交点を見つけます。そして再び計算します

a

$a$ 、

b

$b$ 、

c

$c$ 、そして再び結果はポジティブではありません。同じことが起こります

4 P

$4P$ 、そして

5 p

$5p$ など...つまずくまで

9 p

$9p$ 。

9P=(-66202368404229585264842409883878874707453676645038225/13514400292716288512070907945002943352692578000406921, 
      

        
        
        
      

     58800835157308083307376751727347181330085672850296730351871748713307988700611210/1571068668597978434556364707291896268838086945430031322196754390420280407346469)

見つけるのは簡単ではありませんが、機械の助けを借りれば、単純な幾何学的手順を9回繰り返すだけで済みます。一致する値

a

$a$ 、

b

$b$ 、

c

$c$ すごい：

a=154476802108746166441951315019919837485664325669565431700026634898253202035277999, 
      

        
        
        
      

     b=36875131794129999827197811565225474825492979968971970996283137471637224634055579, 
      

        
        
        
      

     c=4373612677928697257861252602371390152816537558161613618621437993378423467772036

これらは80ビットの数値です！単純なブルートフォースでは、コンピューターで80ビットの数字を見つけることはできませんでした。信じられないように見えますが、これらの膨大な数を単純な表現に貼り付けます

a / （ b + c ） + b / （ a + c ） + c / （ a + b ）

$a /（b + c）+ b /（a + c）+ c /（a + b）$ 私たちは本当に正確に取得します

4

$4$ 。

実際、これらは問題の最小の解決策です。私たちが自分自身にポイントを追加し続ける場合

P

$P$ 、その後、仕切りは単純に成長します。これを証明するのは簡単ではありません。なぜなら、常に減少する可能性があるからです。しかし、楕円曲線の高さ理論により、これらの天文学的数値が実際に方程式の最も単純な解であることを示すことができます。

理論に戻ります。有理数上の楕円曲線にはランクがあります。これは、和音法および接線法に使用し、遅かれ早かれ曲線上のすべての有理点を確実に見つけるために必要な点の数です。楕円曲線（2）のランクは1です。これは、無数の有理点があることを意味しますが、それらはすべて1つだけであり、これは私たちの点にすぎません。

P = （ - 100 、 260 ）

$P =（-100、260）$ 。ランクを計算し、そのようなジェネレーターを見つけるアルゴリズムは簡単ではありませんが、SageMath（現在はCoCalcと呼ばれています）はほんの数行のコードで1秒未満でそれらを実行します。私のコードはここにあります。ソリューション全体を最初から再現しますが、もちろん、組み込みのSageメソッドを使用して楕円曲線を操作します。

私たちの場合、ポイント

P

$P$ 点のように、曲線の楕円部分にあります

m P

$mP$ 正の整数の場合

m

$m$ 。それらは楕円に沿って「円」になり、徐々にその上に均等に分布します。これは非常に成功しています。なぜなら、この楕円形のごく一部が、

a

$a$ 、

b

$b$ 、

c

$c$ ：これは、BremnerとMacLeodから取られた以下のグラフの太字部分です。

ポイント

P

$P$ 、

2 P

$2P$ 、など、選択した部分に横たわらないでくださいが、

9 p

$9p$ -うそ、それがまさに80ビットの正解を獲得した方法です。

BremnerとMacLeodは、交換するとどうなるかを研究しました

4

$4$ 他の何か。ソリューションが大きくなると思われる場合は、結果としてソリューションがどうなるかを確認するまで待ちます

178

$178$ 。 80ビットの代わりに、398,605,460ビットが必要です。はい、これはソリューションの桁数のみです。結果を

896

$896$ 、ソリューションには数兆ビットが含まれます。兆。この無邪気な表情の方程式の場合：

a / （ b + c ） + b / （ a + c ） + c / （ a + b ） = 896

$a /（b + c）+ b /（a + c）+ c /（a + b）= 896$

小さな係数のディオファントス方程式がどのように巨大な解を得ることができるかという印象的な例。これは、a敬の念だけでなく、底なしの感覚を刺激します。 10番目のヒルベルト問題の負の解は、係数が増加する解の成長が計算不可能な関数であることを意味します。計算可能であれば、ディオファントス方程式を解くための単純なアルゴリズムがあり、それは存在しません（単純でも複雑でもありません）。コンプライアンス

4 \か ら

$4 \から$ 80ビット数

178 \か ら

$178 \から$ 数億の数字と

896 \か ら

$896 \から$ 数兆ビットは、この巨大な計算されていない関数の最初の小さなステップの少しのアイデアを与えてくれます。方程式の数値を少し変更すると、決定は私たちの悲惨な小さな宇宙に収まるすべてのものを簡単に上回ります。

これは驚くほどトリッキーな小さな方程式です。

この興味深い記事へのリンクを送ってくれたMrShoorに感謝します。

数学探偵：方程式の正の整数解を見つける

More articles: