Diffie-Hellmanアルゴリズムの量子後の生まれ変わり：ありそうな未来（同質性）

今日は、Diffie-Hellmanプロトコルについて再度説明しますが、より珍しいデザインである同質性に基づいて構築されており、将来の量子コンピューターに対する攻撃に耐性があると認識されています。 数千キュービット程度の束縛状態を保持できる量子コンピューターは、現在使用されているすべての非対称暗号システムの公開鍵から秘密鍵を見つけることができます。 RSAをハッキングするためのキュービットの数は、モジュールのビット数の2倍に等しい（つまり、RSAモジュールと2048ビットの長さの乗算には、4096キュービットが必要です）。 楕円曲線をハッキングするには、「量子鉄」のより控えめな力が必要です：nビットの長さの曲線モジュールで、単純なフィールド（このような曲線は国内署名標準GOST R 34.10-2012およびアメリカのECDSSでも）のECDLP問題を解決するには、6nキュービットが必要です（つまり、256ビットモジュールの場合、〜1536キュビット、512ビット〜3072キュビットが必要です）。 先日、ロシア系アメリカ人の科学者グループが51量子ビットを拘束状態に保つことで世界記録を樹立しました。 そのため、同質性（格子、コード、多変量、およびハッシュベースの署名と同様に）を研究する時間がもう少しあります。

ところで、同質性は、今後数年間でRSAと楕円曲線を置き換えるためのポスト量子アルゴリズムのNISTコンテストで最も有望な候補の1つと考えられています。 Diffie-Hellmanの過去と現在に関する以前の記事は、 ここで読むことができます 。

同質性とは何ですか？

次のように、ある曲線E1の点から別の曲線E2の点（またはそれ自体（E2 = E1と仮定））へのマップ：曲線E1で任意の2つの点A1およびB1を選択し、それらを点A2およびB2曲線E2の場合、同じマッピングは必然的にそれらの合計-点C1 = A1 + B1を正確に点C2 = A2 + B2-マッピングの合計に変換します。 この注目すべき特性は操作の保存と呼ばれ、そのようなマッピングは準同型です。 等値性は有理関数を使用して表すことができます：点（x、y）は座標を持つ点にマッピングされます $$$（\ frac {f1（x、y）} {f2（x、y）}、\ frac {g1（x、y）} {g2（x、y）}）$ （どこ $$${f1、f2、g1、g2}$ -多項式）。

2つの曲線の間にこのようなマッピングがある場合、それらは同質遺伝子と呼ばれます。 同型の特殊なケースは、それ自体の曲線の同型です（endo型）。



同質であるためには、2つの曲線にどのような特性が必要ですか？



テート定理：

グループの次数が等しい場合にのみ、1つの有限体上の2つの曲線は同質です。



例1 （それ自体の曲線の同質性）：



準同型：点と数のスカラー乗算： $$$n * P$ 曲線上 $$$y ^ 2 = x ^ 3 + Ax + B$

たとえば、n = 2および $$$P =（x、y）$ ：



$$$2 * P =（\ frac {x ^ 4-2Ax ^ 2-8Bx-A ^ 2} {4（x ^ 3 + Ax + B）}、\ frac {（x ^ 6 + 5Ax ^ 4 + 20Bx ^ 3 -5A ^ 2x ^ 2-4ABx-8B-A）y} {8（x ^ 3 + Ax + B）^ 2}）$



任意のnに対して、いわゆる除算多項式を使用して、同様の（ただし長い）式を再帰的に取得できます。



例2 （異なる曲線間の同質性）：



曲線を作ろう $$$E1：y ^ 2 = x ^ 3 + x + 1$ フィールド上 $$$Gf（19）$

と曲線 $$$E2：y ^ 2 = x ^ 3 + 4x + 13$ 同じフィールド上。



E1とE2のグループの順序（つまり、曲線上の点の数）は等しい：＃E1 =＃E1 = 21



テートの定理により、等式＃E1 =＃E1は、E1とE2の間に同質性があることを意味します。

jは不変量E1 = 6、jは不変量E2 = 4です。つまり、曲線の点のグループは同型ではありません。

（同型は、画像の1つの要素のみがマップの各要素に対応する準同型の特殊なケースです（つまり、複数の要素が1つに入らない：マップは「1対1」のみです））



E1からE2（例3で取得した場所）にポイントをマッピングする同質性は、次の合理的なマッピングを使用して表すことができます。



ディスプレイ $$$φ：（x、y）$ → $$$（\ frac {x ^ 3-4x ^ 2-8x-8} {x ^ 2-4x + 4}、\ frac {x ^ 3y-6x ^ 2y + 5xy-6y} {x ^ 3-6x ^ 2 -7x-8}）$



たとえば、曲線E1のポイントA1（9、6）およびB1（14、2）を考えます。 それらの合計は、座標（5、6）を持つポイントC1です。 これらを上の式に代入すると、曲線E2にマッピングされますE2上の対応するポイントはA2、B2、C2です。



A1（9、6）→A2（14、1）

B1（14、2）→B2（17、4）

C1（5、6）→C2（8、5）



C2 = A2 + B2であることを簡単に確認できます。 すなわち ポイントC1 = A1 + B1はポイントC2 = A2 + B2に移動します。 怠notでなければ、任意の2点E1 AおよびBとそれらのマッピングφ（A）およびφ（B）からすべての組み合わせを整理し、それらが同様に動作することを確認することができます。



$$$φ（A + B）=φ（A）+φ（B）$



そして、ポイント（2、12）または（2、7）を置き換えるとどうなりますか？ 正しい分数の分母はゼロになります！ これは、これらのポイントがE2の無限大のポイントに到達することを意味します。

E1の無限遠点を考慮する必要があります。 「デフォルト」では、E2の無限遠点に到達します。 これは準同型の基本的な特性です。中立要素（楕円曲線の場合は無限遠点）は中立要素にマッピングされます。 そうでない場合、2つの要素のいずれかがニュートラルである場合、操作の保存は「中断」します。

同質性の次数は多項式の次数と呼ばれます $$$f1$ 表示式で $$$（\ frac {f1（x、y）} {f2（x、y）}、\ frac {g1（x、y）} {g2（x、y）}）$

例2 $$$f1 = x ^ 3-4x ^ 2-8x-8$ すなわち 同質度は3です。度とは、ディスプレイが画像を「圧縮」する回数を意味します。 すなわち E1の3つの異なるポイントが、E2の1つのポイントでこの同質性に表示されます。 無限遠のポイントにマッピングされる多くのポイントは、同質性のコアと呼ばれます。

同質性の計算

そのようなマッピングを見つける方法は？ 特定の曲線の可能な同型の数は、そのポイントのグループ内のサブグループの数に等しいことがわかります。 1971年に数学者Veluによって発明された決定論的アルゴリズムがあります。 多くの式を使用するため、最初に一般的なスキームを示します。



ログイン：

曲線 $$$E1：y ^ 2 = x ^ 3 + Ax + B$ 彼女のサブグループの1つ $$$C$ （同種カーネル）



出力：

曲線 $$$E2：y ^ 2 = x ^ 3 + A'x + B '$ 同質遺伝子 $$$E1$ および合理的なマッピング $$$（\ frac {f1（x、y）} {f2（x、y）}、\ frac {g1（x、y）} {g2（x、y）}）$



アルゴリズムの複雑さ： $$$O$ （＃ $$$C$ ）ステップ＃ $$$C$ -注文 $$$C$



指定： $$$E→E / C$ どこで $$$E / C$ 同質曲線

$$$E$ サブグループを使用して取得 $$$C$



出力で係数を取得します $$$A '$ そして $$$B '$ 等値曲線および分数を含む式の場合。 サブグループCは、曲線のサブグループのいずれかです。 Cは同質性の中核です。そのすべての要素は無限遠点に到達します。 曲線E1が曲線E2と同質である場合、逆も成り立ちます。E2はE1と同質です：反対方向に準同型写像があります。



それでは、なぜすべてを積み重ねたのかを説明しましょう（そして、これを続けます）。

有限体と楕円曲線の乗法群の場合と同じように、同質性については、EDSおよびDiffie-Hellmanの類似物を作成するために使用できる（および使用すべきである）複雑な問題があります。



同質性の課題：

2つの等値曲線が示されています。 $$$E1$ そして $$$E2$ 異なるj-不変式を使用します。 それらの間の同質性を見つけることが必要です。



2つの曲線があり、それらが同質遺伝子であることがわかっている場合（および、それらのグループの順序が等しい場合はそうです）、どのサブグループを使用してこの同質性を取得できるかはわかりません。 明らかに、サブグループの数は非常に大きくなければならず、サブグループをVelu 'アルゴリズムに代入する単純な列挙によって同質性を見つけることは計算上困難です。



Velu 'アルゴリズム：



ログイン：

曲線 $$$E1：x ^ 3 + Ax + B$ 彼女のサブグループの1つ $$$C$ （コア同質性）



1.ポイントを無限にドロップします

2.見つける $$$C_2$ -偶数次のポイントのセット $$$C$ 。

$$$R$ -他のみんな

3.壊れる $$$R$ 2つの部分に- $$$R _ {+}$ そして $$$R _ {-}$ ：ポイントP-の場合 $$$R _ {+}$ 、それの逆は $$$R _ {-}$

4.多くの $$$S = C_2∪R _ {+}$



すべてのポイントについて $$$Q =（x_Q、y_Q）$ から $$$S$



$$$g_ {Q} ^ x = 3x_ {Q} ^ 2 + A$

$$$g_ {Q} ^ y = -2y_ {Q}$



$$$if（Q = -Q）$

$$$v_ {Q} = g_ {Q} ^ x$

$$$その他$

$$$v_ {Q} = 2g_ {Q} ^ x$



$$$u_ {Q} =（g_ {Q} ^ y）^ 2$



$$$v = \ sum_ {Q∈S}（v_ {Q}）$

$$$w = \ sum_ {Q∈S}（u_ {Q} + x_ {Q} v_ {Q}）$



オッズ $$$A '$ そして $$$B '$ 等値曲線の方程式について $$$E '$ ：

$$$A '= A-5v$

$$$B '= B-7w$



だから、同質遺伝子曲線を知っています。 表示の計算方法 $$$（x、y）$ → $$$（α、β）$ ：



$$$α= x + \ sum_ {Q∈S}（\ frac {v_Q} {（x-x_Q）} + \ frac {u_Q} {（x-x_Q）^ 2}）$

$$$β= y-\ sum_ {Q∈S}（u_Q \ frac {2y} {（x-x_Q）^ 3} + v_Q \ frac {y-y_Q} {（x-x_Q）^ 2}-\ frac { g_Q ^ xg_Q ^ y} {（x-x_Q）^ 2}）$



Velu 'アルゴリズムの出力：

オッズ $$$A '$ 、 $$$B '$ 点を表示するための等値曲線と公式 $$$（x、y）$ → $$$（α、β）$



例3 （Veluのアルゴリズム。例2でどのように同質性が得られたか）：



ログイン：

$$$y ^ 2 = x ^ 3 + x + 1$ フィールド上 $$$Gf（19）$ およびサブグループ $$$C$ ：{ $$$O$ 、 $$$（2、7）$ 、 $$$（2、12）$ }



1.ポイントを無限にドロップします

2.に偶数ポイントがない $$$C$ いや

3.を選択します $$$R _ {+}$ ポイント $$$（2、7）$ 。 ポイント $$$（2、12）$ -それは反対です（7 = -12 mod 19のため）

4.多くの $$$S$ = { $$$（2、7）$ }



ワンステップサイクル：（ $$$S$ 1つの要素のみ：ドット $$$Q =（2、7）$ ）：



$$$Q =（2、7）$ その座標 $$$x_Q = 2、y_Q = 7$

$$$g_Q ^ x = 3 * 2 ^ 2 + 1 = 13$

$$$g_Q ^ y = -2 * 7 = -14 = 5$$$$mod$$$$19$

$$$v_Q = 2 * 13 = 26$$$$mod$$$

$$$u_Q = 5 ^ 2$$$$mod$$$

$$$v = 7$

$$$w = 6 + 2 * 7 = 20 = 1$$$$mod$$$$19$

$$$A '= A-5v = 1-5 * 7 =-34$$$$mod$$$$19$ = $$$4$

$$$B '= B-7w = 13$



合理的なマッピングを計算するためだけに残ります。 $$$（x、y）→（α、β）$ ：

$$$α= x + \ frac {7} {x-2} + \ frac {6} {（x-2）^ 2} = \ frac {x ^ 3-4x ^ 2-8x-8} {x ^ 2 -4x + 4}$



同様に、βの式を共通分母に与えます。

$$$β= \ frac {x ^ 3y-6x ^ 2y + 5xy-6y} {x ^ 3-6x ^ 2-7x-8}$



出力：

同質曲線の係数： $$$A '= 4、B' = 13$

ディスプレイ $$$（x、y）→（α、β）$ （上記を参照）。

同程度の大規模な計算

Veluアルゴリズムには落とし穴があることは簡単にわかります。セットのすべてのポイントを通過するまでサイクルで動作します $$$S$ 。 これは、ステップ数が同質核の半分（サブグループ $$$C$ 、入力に供給されます）、より少ない順序 $$$C$ 。 Veluは比較的小さなサブグループしか使用できないため、許容可能な時間内にアルゴリズムのすべてのステップを実行することができます。これにより、同質性の暗号化アプリケーションが複雑になります。 幸いなことに、たとえグループが $$$C$ 素晴らしい秩序があります $$$C$ しかし、特定の構造を持っています：＃ $$$C$ -少数の程度 $$$l$ 、つまり $$$l ^ e$ 。 この場合、アルゴリズムはeステップで構成され、それぞれが次数の同質性 $$$l$ by Velu 'およびポイントと数値の1つのスカラー乗算。 として $$$l$ 通常、2または3を選択します。



指定：曲線 $$$E '$ 同質遺伝子 $$$E$ サブグループを使用して取得 $$$C$ 代わりに $$$E$ / $$$C$ 、ドットでマークする方が便利な場合があります $$$G$ -ジェネレーター $$$C$ ： $$$E / <$$$$G$$$$>$ 。



させる $$$G$ -注文のポイント $$$l ^ e$ 。 同質性を計算する必要があります $$$φ：E→E / <$$$$G$$$$>$ 。

同質性の分解 $$$φ$ それぞれが学位を持つ同種のシーケンス $$$l$$$$φ_{e-1} *φ_{e-2} * ... *φ_{0}$ ：

$$$φ_0：E、G_0 = G$

$$$φ_i：E_ {i + 1} = E_i / <$$$$l ^ {e-1-i} G_i$$$$>$ 、 $$$G_ {i + 1} =φ_i（G_i）$



例4

次数の周期的グループの等値性を計算したい $$$l ^ 4$

グループにVelu 'アルゴリズムを1回適用する代わりに、同種性の程度を考慮して4回適用します。 $$$l$ そして、ポイントに数値を3回掛けます。 させる $$$G_0$ -このグループのジェネレーター、順序のポイント $$$l ^ 4$ 。



$$$φ_{3}$ * $$$φ_{2}$ * $$$φ_{1}$ * $$$φ_{0}$ ：



$$$φ_0：E_1 = E_0 / <$$$$l ^ {3} * G_0$$$$>$ 、 $$$G_1 =φ_0（G_0）$



$$$φ_1：E_2 = E_1 / <$$$$l ^ {2} * G_1$$$$>$ 、 $$$G_2 =φ_1（G_1）$



$$$φ_2：E_3 = E_2 / <$$$$l ^ {1} * G_2$$$$>$ 、 $$$G_3 =φ_2（G_2）$



$$$φ_3：E_4 = E_3 / <$$$$G_3$$$$>$



そのため、 非常に大きな次数の周期的グループの同質性を計算できるようになりました。 たとえば、注文のグループがある場合 $$$2 ^ {256}$ そして、そのジェネレータを知っていれば、アルゴリズムを256ステップで実行します。

練習：超特異曲線間の同質性

2つの同形曲線は、その曲線に対して同じj不変量を持っていることを思い出してください $$$y ^ 2 = x ^ 3 + Ax + B$ 彼は平等です $$$1728 \ frac {4A ^ 3} {4A ^ 3 + 27B ^ 2}$

同型曲線間の変換を見つけることは特に難しいことではないため、同型性の問題は本質的に同型曲線の異なるクラス間で同型性を見つける問題です（これらのクラスのそれぞれは対応するj不変量として表すことができます）。

どの曲線が同質性に関心がありますか？ 結局、楕円ディフィー・ヘルマンとEDSには禁則曲線族があることがわかっています：超特異、異常、滑らかな秩序など。 -すべてにとって、ECDLPの問題は比較的簡単に解決できます。 そのような不愉快なクラスは同質性のために存在しなければなりません。 難しいタスクはECDLPではないため、ここでのみ状況は完全に異なります。 明らかに、滑らかな次数の曲線を使用して、サブグループを増やす必要があります。 さらに、2010年に、ウォータールー大学の研究者は、通常の曲線を使用することは「量子」の観点から安全ではないことを発見しました。 これらは、フロベニウストレースtがt mod p = 0である曲線であることに注意してください。ここで、pは曲線のフィールドの特性です（フロベニウストレース自体は、曲線のグループの順序に関連しています＃ $$$E（GF（p ^ n））$ およびフィールド関係＃ $$$E（GF（p ^ n））= p ^ n + 1-t）$ 。 さらに、それらのみを検討します。



曲線のどのフィールドが最適に使用されますか？ 答えはすぐに頼みます-古き良き平原 $$$Gf（p）$ 。 しかし、残念ながら、超特異曲線は $$$Gf（p）$ 異なるj不変式が少なすぎます：〜 $$$\ sqrt {p}$ 。 一方、フィールドについて $$$Gf（p ^ 2）$ 、j-不変の数＃ $$$S_ {p ^ 2} = \ lfloor p / 12 \ rfloor + a$ どこで $$$a∈$ { $$$1、2、3$ }



このような曲線には興味深い特性があります。

固定次数の同質グラフは正しいです。 （つまり、各頂点には同じ数のエッジがあります）

あらゆる素数に対して $$$l$ 曲線の点のグループの順序を分割する $$$l + 1$ 秩序の核を持つ同質性 $$$l$ 。 （つまり存在します $$$l + 1$ 注文のサブグループ $$$l$ 同質性を得ることができます）



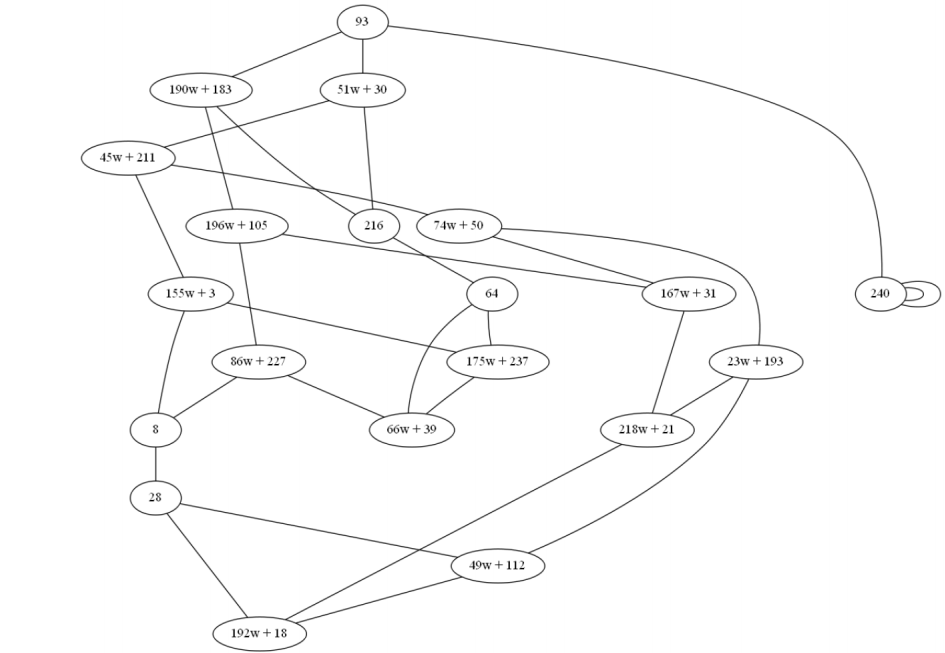
例5 （例とグラフ画像-Dr. Fre Vercauteren）

フィールドを考慮してください $$$Gf（{241 ^ 2}）$

既約多項式を選択します： $$$x ^ 2-3x + 7$

j-不変量のセットは次のとおりです。

$$$S_ {241 ^ 2}$ = {93、51w + 30、190w + 183、240、216、45w + 211、196w +

105、64、155w + 3、74w + 50、86w + 227、167w + 31、175w + 237、66w + 39、8、23w + 193、218w + 21、28、49w + 112、192w + 18}

番号＃ $$$S_ {241 ^ 2}$ = 20



次数曲線の場合＃ $$$E$ = 57600 = $$$2 ^ 8 * 3 ^ 2 * 5 ^ 2$ ：



同質度 $$$l = 2$ ：

各曲線には次数2の3つの同質性があります





同質度 $$$l = 3$ ：

各曲線には次数3の4つの同型があります





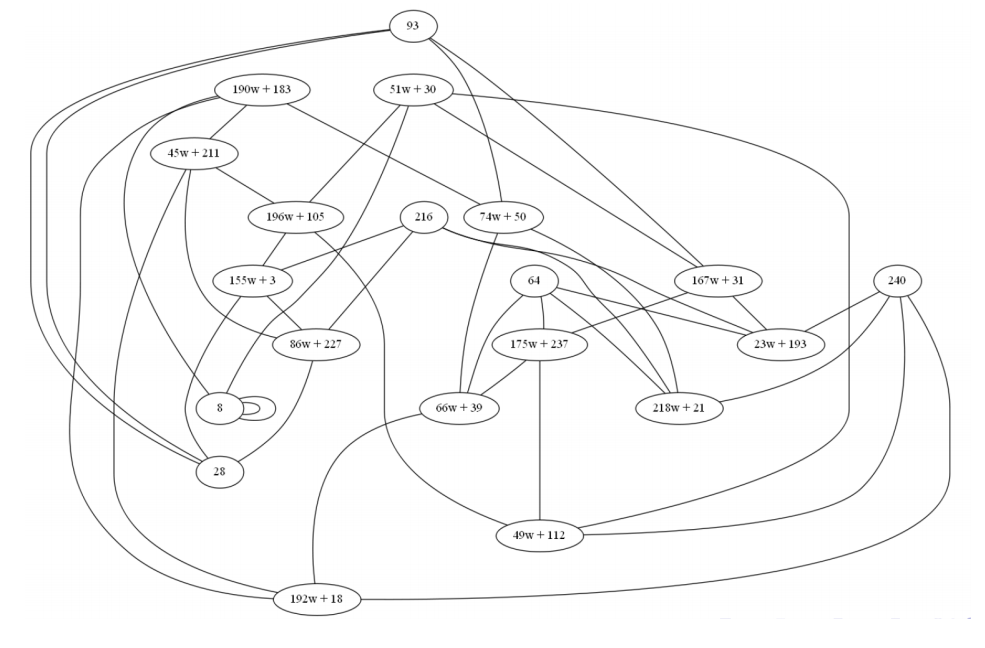
同様に $$$l = 11$ 。

各曲線には、次数11の12の同型があります。



攻撃者が解決しなければならない困難なタスクは、次のように定式化できます。2つの曲線を知る $$$E1$ そして $$$E2$ （つまり、2つを知っている $$$j$ 不変量 $$$j1$ そして $$$j2$ ）、それらの間の同質グラフでパスを見つけます。 本質的に、曲線c間の同質性を取得する方法を見つける $$$j1$ および曲線c $$$j2$

超特異等値ディフィー・ヘルマン（SIDH）

定義：

もし、ポイントを掛けるとき $$$P$ 曲線 $$$E（GF（p ^ m））$ nを掛けると、無限遠点が得られ、そのような点はnねじれ点と呼ばれます

Nねじれサブグループ $$$E [n]$ ：

$$$E [n] =$ { $$$P∈E（GF（p ^ m））：n * P = O$ }

このサブグループは、無限大のポイントとすべてのnねじれポイントで構成されます。

明らかに、nねじれ点は、その順序がnを余りなく分割する場合の点です。



$$$E [n]$ 直接積に同型 $$$（Z / nZ）×（Z / nZ）$ nがpと互いに素である場合。 （つまり、注文 $$$E [n]$ 等しい $$$n ^ 2$ ）



フィールド選択 $$$Gf（p ^ 2）$ SIDHの曲線の場合：

させる $$$f$ -少数、および $$$l_a、l_b$ -小さな素数。

フィールドを特徴付けるとき $$$p = l_a ^ {e_a} * l_b ^ {e_b} * f±1$ 曲線順 $$$E$ ：＃ $$$E =（l ^ {e_a} * l ^ {e_b} * f）^ 2$

$$$E [l ^ {e_a}]$ 含む $$$l_a ^ {e_a-1}（l_a + 1）$ 順序の循環サブグループ $$$l_a ^ {e_a}$



させて $$$l_a = 2、l_b = 3$

フィールド特性 $$$p = 2 ^ {m} * 3 ^ {n} * f±1$ 、そしてnとmを選択して、 $$$2 ^ {m}$ ほぼ等しかった $$$3 ^ {n}$

ねじりサブグループ $$$E [2 ^ m]$ そして $$$E [3 ^ n]$ ⊆ $$$E [p ^ 2]$



$$$E [2 ^ m]$ 含む $$$2 ^ {m − 1} * 3$ 順序の循環サブグループ $$$2 ^ m$

$$$E [3 ^ n]$ 含む $$$3 ^ {n − 1} * 4$ 順序の循環サブグループ $$$3 ^ n$



ポイントを選ぶ $$$P_a、Q_a$ -の基礎 $$$E [2 ^ m]$ （つまり、組み合わせを使用する $$$x * P_a + y * Q_a$ 任意のポイントを取得できます $$$E [2 ^ m]$ ）およびポイント $$$P_b、Q_b$ -の基礎 $$$E [3 ^ n]$



SIDHのドメインパラメーター（通常の楕円曲線のドメインパラメーターのアナログ）：

曲線 $$$E$ および2つのベース{ $$$P_a、Q_a$ }および{ $$$P_b、Q_b$ }。 彼らはアリス、ボブ、攻撃者に知られています。





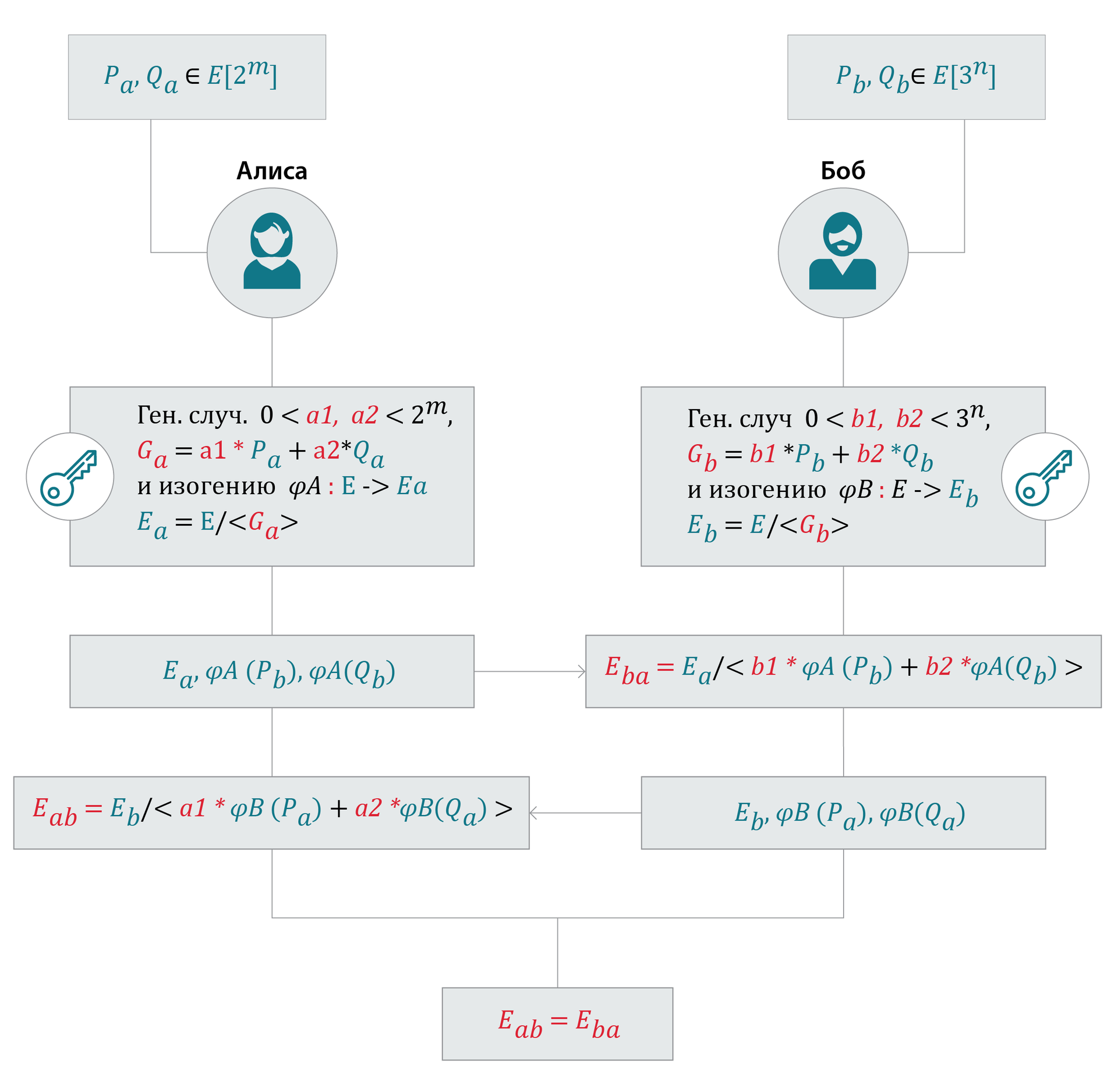
（注： $$$E_ {ab} = E_ {ba}$ 同型まで：曲線の係数は異なる場合がありますが、j不変量は同じです）



開始者（アリス）は、基底を使用してペアを生成します $$$P_a、Q_a$ 。

アリスはランダムに生成します $$$a1、a2：0 <a1、a2 <2 ^ m$ （ $$$a1、a2$ 両方とも倍数ではありません2）

$$$a1、a2$ アリスの秘密鍵です。

次に、ポイントを計算します $$$G_a = a1 * P_a + a2 * Q_a$

そして、その助けを借りて同質性を計算 $$$φA：$$$$E→E_a = E$ / < $$$G_a$ >、

次に同値を使用して変換します $$$φA$ 曲線上のボブの基礎 $$$E_a$ ： $$$φA（{P_b}）、φA（{Q_b}）$



アリスの秘密鍵： $$$a1、a2$

アリスの公開鍵：曲線 $$$E_a$ とポイント $$$φA（{P_b}）、φA（{Q_b}）$



Bobも同様の手順を実行します（図を参照）。

ボブの秘密鍵： $$$b1、b2$

ボブの公開鍵：曲線 $$$E_b$ とポイント $$$φB（{P_a}）、φB（{Q_a}）$



アリスは公開鍵をボブに送信します

ボブはポイントを計算します $$$b1 *φA（{P_b}）+ b2 *φA（{Q_b}）$ 彼女の助けを借りて

同質曲線 $$$E_ {ba} = E_a$ / < $$$b1 *φA（{P_b}）+ 2 *φA（{Q_b}）$ >



次に、ボブはアリスに公開鍵を送信し、アリスも同様に曲線を計算します $$$E_ {ab}：$

$$$E_ {ab} = E_b$ / < $$$a1 *φB（{P_a}）+ a2 *φB（{Q_a}）$ >



共有秘密を取得するために、アリスは次からj不変量を計算します $$$E_ {ab}$

からボブ $$$E_ {ba}$ 。

セキュリティとキーのサイズ

攻撃を成功させるには、少なくとも1つのグラフ（AliceまたはBob）でパスを見つける必要があります。 このタスクは、古典的なコンピューターと量子コンピューターの複雑さの度合いが異なります。

古典的な難易度：アリス $$$\ sqrt {2 ^ m}$ ボブ $$$\ sqrt {3 ^ n}$

量子難易度：アリス $$$\ sqrt [3] {2 ^ m}$ ボブ $$$\ sqrt [3] {3 ^ n}$

したがって：

従来のセキュリティ= $$$min（\ sqrt {2 ^ m}、\ sqrt {3 ^ n}）≈\ sqrt [4] {p}$ 操作

量子セキュリティレベル= $$$min（\ sqrt [3] {2 ^ m}、\ sqrt [3] {3 ^ n}）≈\ sqrt [6] {p}$ 操作



キーサイズ：



公開鍵：

ポイントPおよびQ

係数AおよびB曲線



〜8 * $$$log_2（p）$ 少し

〜6 * $$$log_2（p）$ ビット（最適化：Costello、Crypto 2016）



フィールド特性長= 768ビット：

768/6 = 128ビット量子セキュリティレベル

768/4 = 192ビットのクラシックセキュリティ

キーの長さ6 $$$log_2（p）$ ビット= 4608ビット= 576バイト



フィールド特性長= 1536ビット：

1536/6 = 256ビットの量子セキュリティレベル

1536/4 = 384ビットのクラシックセキュリティ

キーの長さ6 $$$log_2（p）$ ビット= 9216ビット= 1152バイト

性能

128ビットの量子セキュリティレベルの最適な結果（フィールド特性 $$$p = 2 ^ {372} 3 ^ {239}-1$ つまり $$$p$ 〜 $$$2 ^ {768}$ ）：



3.4 GHzのIntel Haswellの場合：

いずれかの当事者（アリスまたはボブ）の1億メジャー未満で計算

（モンゴメリ曲線と射影座標が使用されます）



1 GHzのARM7 Beagle Board Black Cortex-A8チップの場合：

リードタイム-1.5秒。 NEON SIMD命令を使用する場合、0.2秒。

参照：

1.「Isogeniesに基づく公開鍵暗号システム」、Alexander Rostovtsev、Anton Stolbunov、2006



2.「量子準指数時間における楕円曲線同型の構築」Andrew M. Childs、David Jao、Vladimir Soukharev、2010



3.「超特異楕円曲線同種からの量子抵抗性暗号システムに向けて」David Jao、Luca De Feo、2011



4.「超特異同型ディフィー・ヘルマンの効率的なアルゴリズム」Craig Costello、Patrick Longa、Michael Naehrig、2016



5.「NEON-SIDH：ARMでの超特異同質性Diffie-Hellman鍵交換プロトコルの効率的な実装」R. Azarderaksh、D。Jao、2016



6.「公開鍵暗号の数学」スティーブン・D・ガルブレイス、ケンブリッジ大学出版局