目次。
自動vs自動
専門家は、オートマトンをかなり広範囲に分類します:決定論的および非決定論的、有限および無限、マイルおよびムーア、同期および非同期など ただし、ユーザーの観点からは、メガロポリスで個人用の車が必要かどうかを自分で判断したい場合と同じです。シリンダーの数とインジェクターについては説明されます。
ポピュラライザーとして、使用の観点から、マシンは2つの関連するカテゴリーに分けられます。
- 数学的抽象化としてのオートマトン、オートマトンを実装するためのメソッドもここに含まれます。
- 数学にも基づいた、デジタルロジックデバイス(回路およびプログラム)を設計するための一連の手法およびアプローチとしてのオートマトン。
これらのアプローチの関係は簡単に説明できます。
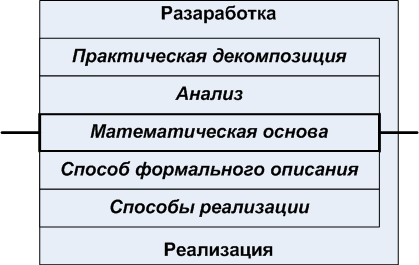
図1.コンピューター支援設計とコンピューター支援実装
同僚とのコミュニケーションから明らかになる限り、マシンを次のように考えるフォーマリストのカテゴリーがあります。
- 説明がUML状態図または同様の説明メソッドのフレームワークに厳密に適合しなければならないエンティティ、つまり、個別の機能として定義されたノードのセット、信号のセット、およびそれらの間の関係を定義する正式なテーブルを持っているエンティティ
- 自動的に実装されるプログラムの概念は、実装技術の1つであるboost.statechart、visualStateなどに属することに厳密に制限されています。
明らかに、このようなアプローチは、自動指向のパラダイムにより開かれる機会のスペースを狭め、オートマトンに対するこのような態度は、修正可能な一般的な科学資料の不足によってのみ説明できます。
マシンを使用したいのは、シンプルさと同時に設計の深さです。前の部分では、モジュールの自動指向設計の基礎は、タスクを操作オートマトン(OA)と制御オートマトン(UA)に分割することであり、操作オートマトンは下位レベルの操作オートマトンとその制御オートマトンに再分割できることを示しました。 。
オペレーティングマシンは、何らかのアクションを最適に実行できる半製品ですが、同時に、このアクションを実行するタイミングとパラメーターを「気にしません」。オペレーティングマシンは、任意の有効なパラメーターを使用してこれを実行できます。 ALU運用マシンの優れた例。
次に、操作オートマトンのパラメーター化と起動は、制御オートマトンの肩にかかっています。多段分割により、複雑な制御オートマトンを得ることを回避できますが、鉄のロジックではなく、最も理解しやすい機能を持ついくつかの単純な制御オートマトンに置き換えます。
実装この場合、制御オートマトンは完全に非自動または自動である場合がありますが、次のような属性はありません:状態が個別の関数、シグナルテーブル、および対応する遷移にロールアップされます。最後に、プログラムはすべて自動ですが、すべてのプログラムが自動的に実装されるわけではありません。
しかし、その場合、自動的に実装されるプログラムとはどういう意味ですか?
実装:自動と非自動。
自動実装プログラムの主な属性は次のとおりです。
- 明確に区別され明確に制限された状態の存在。動作では、プログラムは常にある1での状態。
- プログラムの現在の状態は、マシンの内部状態と呼ばれる単一の変数によって記述されます。
この定義は、いわば不変であり、その実施形態は異なっていてもよい。「自動化プログラムの実装方法」セクションでは、言われたことを説明するいくつかの例を検討しますが、一般的に本質は明らかです。
現在、プログラムを自動実装プログラムに帰属させる明確な基準がありますが、誰かが尋ねます:自動実装のキャッチは何ですか、なぜそれがより価値があるのですか?
自動実装されたアルゴリズムと実装されたアルゴリズムを区別する主なものは、私たちの精神の領域、より正確には、私たちの考え方にあります。同僚として適切に発言した:
« , , , , . « » ( ..) , ».
分析関数の動作は、表またはグラフの形式で表すことができます。入力に何かがあり、出力に1対1の対応があります。ただし、デジタルデバイスの大部分は、分析機能をブリックとして使用するため、その結果、動作が既に内部状態に依存しているプログラムを取得できます。つまり、分析関数を使用しても「わかりやすさ」の問題は解決せず、別のレベルに移動します。
「理解可能性」という用語と人間の思考の特徴を説明するために、まったく同じ抽象アルゴリズムがどのように自動および非自動で作成、実装されるかを検討することを提案します。
a)
b)
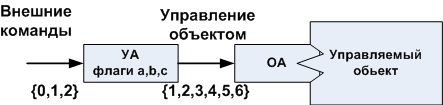
図2.制御デバイスの一般的な例(a)およびこのデバイスの動作を説明するグラフ図(b)。
特定のプログラムは、特定のデバイスを制御するように設計されています。図に示すように。 2(b)。 UAは、通常は文字セット{0,1,2}で示される外部コマンドを処理し、オペレーティングマシンを制御する一連のマイクロ命令に変換します。マイクロ命令とは、効果を得るために必要な一連のコマンドを意味します。マイクロ命令の各セットは、条件付きでシンボル{1,2,3,4,5,6}で示されます。制御マシンのフラグ{a、b、c}は、管理対象オブジェクトの状態を監視し、それに応じて、入力コマンドの処理モードを決定します。
これはメモリを備えたデジタルデバイスであるため、図2で説明されているアルゴリズムは、アルゴリズムの実装が非自動であるという事実にもかかわらず、実際にはオートマトンです。これは、明示的に割り当てられた状態が存在しないという事実につながり、その結果、現在の状態はフラグによって暗黙的に決定されます。さらに、グラフ方式によるプログラムの記述自体はオートマトンの原理と矛盾せず、自動的に実装されるプログラムはグラフ方式によって記述でき、そのような例があります。グラフ図に関連する主な問題は、ダイナミックの観点からHSが記述したプログラムの理解度が低いことです。プロセスは時間内に進行します。
念頭に置いておくと、これは非常に単純な例ですが、どの出力信号が入力信号0に対応するかを明確に言うことはできません。これは、フラグの状態、より正確にはフラグbに依存するためです。前の入り口にあったもの。また、どの出力シーケンスが入力シーケンスに対応するかをすぐに言うのは簡単ではありません:2,1,0,2,1,0。これを行うには、実際にアルゴリズムを実行する必要があります。
入力信号と出力信号の完全な対応、つまり関数を表形式で記述するためには、完全なテストを実行する必要があり、さらに、すべての種類の入力の組み合わせが順番に並べ替えられた2信号シーケンスの形式で結果が得られます。
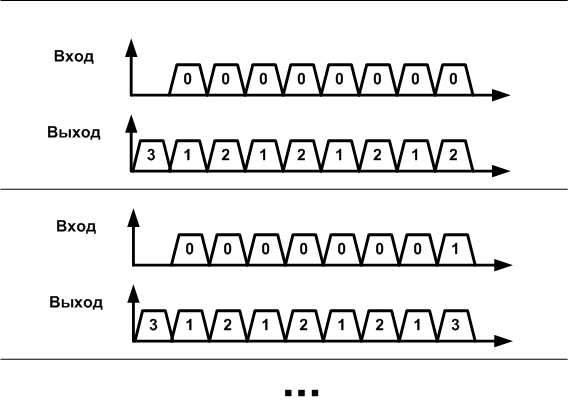
図3.タイミング図-メモリを搭載したシステムの動作を説明する方法。
3つのバイナリフラグを使用すると、すべての可能なオプションを説明するために、3つの入力文字のアルファベットに対して、以前の8つの文字を追跡することはできません(ただし、それ以上ではないため)、入力信号のセットと状態のセットの積と呼ばれる6561図を与える必要があります状態の数と入力信号のアルファベットのサイズが大きくなると、幾何学的に大きくなります。
プログラムの自動実装により、 状態図を使用してプログラムを記述することができ、状態図と遷移により、メモリを備えた動的システムの分析に対して根本的に異なるアプローチが提供されます。 図2bに示すアルゴリズムを実装するオートマトンを構築します(方法は指定しません。これは別の会話のトピックです)。これは、図4に示す状態図と遷移図で説明されます。状態。

図4.図2に示したアルゴリズムに対応する状態と遷移図
このチャートの使用は非常に便利です。入力文字のみが遷移に影響するため、追加の条件はありません。 つまり、図2の実装の入力シンボルへの応答を分析するには、各反復でのフラグの現在の状態を取得する必要があります。図4に示すように実装されたデバイスの動作を分析するには、この図以外は必要ありません。
これは、次の自動化アプローチの重要な利点です。
時間軸外の動的プロセスを調べます。
人間の脳は、同じ表が一度に1桁ずつ表示される場合よりも、数字の表で作業しやすいように配置されています。 最初のケースでは、人は複雑なパターンを識別できます; 2番目のケースでは、テーブルを周期的にスクロールしても、最も単純なパターンを除き、パターンをほとんど決定できません。
例を考えて、一連のコマンドを考えてみましょう
Set_position(6,0); Line_to (1,0); Line_to (1,1); Line_to (-1,2); Line_to (4,0); Line_to (1,-3); Line_to (3,0); Line_to (0,6); Line_to (-11,0); Line_to (-1,1); Line_to (-2,0); Line_to (3,-2); Line_to (0,-2); Line_to (1,2); Line_to (2,0); Line_to (-1,-2); Line_to (1,-1);
同意して、それぞれのアクションはシンプルなデザインです。 ただし、すべてのアクションを完了していないため、何が成功するかは言えません。 このアルゴリズムの結果は図に示されています。 5 a

a)b)
図5.コマンドのシーケンスの実行結果(a)、およびエラーが発生した場合の同じシーケンスの実行結果(b)
同時に、計算に誤りがあり、たとえば、2行目の最初のステートメントで(1、-3)の代わりに値(2、-3)を示します。作業の結果は異なります(5 b)が、プログラムのテキストを見ると理解できません。 そして、これは実行後すぐに結果を見ることができるシンプルなケースです。 結果を常に1行として表示する場合、またはグラフィックではなく数字を扱う場合、間違いはそれほど明白ではありません。
これは、 動的なプロセスと呼ばれる人間の脳にとって簡単なタイプの情報ではなく、 一連のアクション (例では別々の行)であり、重ね合わせの結果として何らかの期待される結果 (例では図)をもたらします。
時間軸外の動的プロセスの良い例は、周波数領域の信号の分析です。 図6の信号を検討してください。いくつかの方法で、オートマトンのタイムダイアグラムと比較できます。 これも一連のアクションです。信号は0を超え、上昇し、最大値に達し、低下し、再び0を超えました。
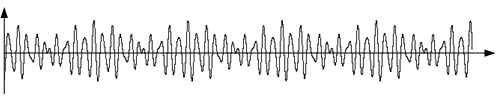
図6.オートマトンのタイムダイアグラムに類似した信号グラフ。
明らかに、これは周期的な信号であり、いくつかの正弦波で構成されていると推測することさえできますが、どの正弦波かを言うことは困難です。
同時に、スペクトルは信号構造のアイデアを直接提供します。

図7.図6に示す信号のスペクトル。
スペクトルは、この点でオートマトンダイアグラムと比較できます。 時間内に実行されるプロセスの中心にあるものの静的な記述が含まれています。 スペクトルと状態図および遷移図の両方により、時間軸外のプロセスを分析し、一連のステップとしてではなく、全体としてカバーすることができます。
ちょっとした数学
厳密な数学的カテゴリとしての状態図と遷移により、詳細な分析が可能になります。
図5の状態図と遷移図で説明されているプロセスを分析しましょう。 このためには、同型オートマトンの概念が必要です。 同型オートマトンは、オートマトンを意味する数学用語であり、実際には名前が変更された状態や信号を持つ同じオートマトンです。

図8.同型オートマトン。
問題の条件から、アルゴリズムが処理するプロセスについては何も知らないことがわかります。 2 b。 それにもかかわらず、図に示す分析は 4つの図を使用すると、2つの非常に類似したクラスターを選択できます。クラスター間の切り替えは、主に信号0によって行われます。
元のオートマトンと同型のオートマトンを構築しますが、その状態番号は図9に示すように名前が変更され、指定されたクラスターの概要が示されます。 状態4,5,6が括弧内にあるクラスターでは、最初のクラスターと同じ状態です。

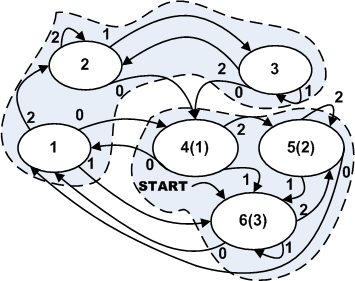
図9.図4に示したものと同形のオートマトン
図に示すように、元のオートマトンを2つの並列オートマトンに分解(分割)します。 10。
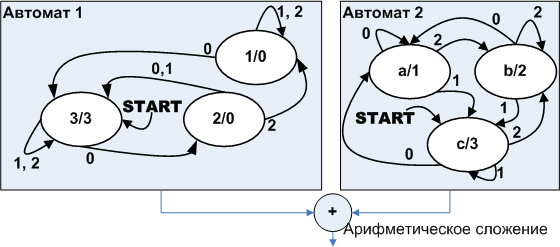
図10.図9に示すマシンの並列分解
各マシンの出力シンボルには、状態の名前の後にスラッシュが付けられます。 得られたオートマトンの出力シンボルは算術的に加算され、同じ入力データを持つ元のオートマトンの出力のシンボルに完全に対応する1〜6の出力が得られます。 このオートマトンの接続は、パラレルコンポジションと呼ばれます。
自動2に注意してください。 どのような状態であっても、入力シンボル0はシンボル1の出現につながり、入力シンボル1はシンボル3の出現につながり、シンボル2はシンボル2の出現につながります。つまり、これは組み合わせ回路であり、出力シンボルの配列です。配列インデックスは入力文字です。 図に示すようなオートマトンを描きましょう。 11
図11.図に示したオートマトンと同等のオートマトン 10
出力シンボルは特定の一連のマイクロ命令をエンコードしているため、数学者の目を通して問題を見て、各マイクロ命令にインデックスがあるこの実装されたマイクロ命令の配列があると想像すると、ここでは算術変換は不適切であるように見えるかもしれません間違いなく変革しています。
特に、入力のシンボル0,1,2と出力のシンボル1,2,3は異なるアルファベットを参照しているため、出力から入力にシンボル1を取り込んで送信することは不可能です。 ただし、入力記号と出力記号が同じアルファベットに属するオートマトンが存在する場合があります。その場合、オートマトンの出力記号をその入力に供給することができます。 これはフィードバック構成と呼ばれます 。 講義のパラグラフ4.7は、このような構成に専念しています。
問題の条件から、アルゴリズムによってモデル化されたオブジェクトの性質は不明でした
図 2b、およびそれにもかかわらず、オートマトンを分析および分解することにより、シミュレートされた現象は最終結果に寄与する2つの独立したプロセスに基づいていることがわかりました。 また、抽象的な例の場合、これは興味深い観察にすぎませんが、特定のタスクの場合、上記の分析はシミュレートされた現象の明白でない側面を明らかにする可能性があります。したがって、プログラミングの観点だけでなく、工学の観点からも興味深いです。 エンジニアにとって、現象の根底にあるプロセスを理解することで、開発中のデバイスの見方を修正し、本質を打ち破る独自の技術的ソリューションを得ることができます。
考慮された例は、オートマトンの別の重要で有用な特性、 等価オートマトンの概念に触れています。 事実は、異なる数の状態を持つ任意の多くのオートマトンが存在できることです(つまり、同型オートマトンについては話していない )。これは、同じ入力シーケンスに対して同じ応答を提供します。 したがって、「ブラックボックス」にそれらを配置する場合、入力に異なるシーケンスを適用し、応答を分析することによってそれらを区別することはできません。
この場合、オートマトンの中には内部状態の数の点で「無駄」なものもあれば、「経済的」なものもあります。 同等のオートマトンの全セットの中には、可能な限り少ない数の状態を持つオートマトンがあり、これは最小オートマトンと呼ばれます。 さらに、任意のオートマトンから同等の最小値を取得するためのアルゴリズム手法があります。 特に、このプロパティは、状態図と遷移を作成するときに、状態の数の最小化を追いかけるべきではなく、最も明確で完全な図を達成する必要があることを意味します。 また、理解の容易さと実装の容易さはしばしば関係しますが、この例のように、結果を一対のオートマトンとして提示する方が視覚的になることがあります。 その後、数学アルゴリズムを使用して、同等の最小オートマトンを見つけることができます。
この記事ではオートマトンの理論を検討するつもりはないので、オートマトンで実行できる基本的な数学的操作を簡単にリストします:合成、分解、最小化、マイクロプログラムからのオートマトンの取得、オートマトンに基づくマイクロプログラムの取得、オートマトンの代数演算(追加、オートマトンの比較)、シミュレートするオートマトンなどの構築。これらの変換を実行するための理論的な正当化と方法は、たとえばここにあります 。
今日の部分を要約します。 非手動プログラミングの特徴は、任意の時点でのプログラムの状態がソフトウェアカウンターだけでなく、多数の内部フラグによって記述されることです。 非自動スタイルのプログラムの状態という用語は、形式化できない概念の一種です。つまり、プログラムがTKを必要とするすべてのアクションを実行するということです。 それにもかかわらず、上で示したように、プログラムの非自動スタイルでも、数学的にはオートマトンです。 数学的な意味での状態がありますが、これらの状態はどこにも記述されていません。 いくつあるのか、それらの間の関係は不明です。 各新しいバイナリフラグを追加すると、可能な状態の数が幾何学的に増加します。 この場合、多くの新しい状態は、プログラムがどんな状況でも決して入らない到達不可能な状態になりますが、この場合、次の状態を明示的に選択しないため、すべてのフラグの重ね合わせであることが判明します、少なくとも1つのフラグのロジックが正しくない場合、プログラムは禁止状態にジャンプし、これを示す指標はありません。 積極的に変化しているフラグを処理し、プログラムのパスが曲がりくねっており、多くの分岐を通過し、すべての可能な入力文字のすべての分岐オプションがテストされるまで、10回目の反復後にプログラムが最終的になると信じることができます私たちが期待する状態で。
自動実装の場合、 状態は数学的なカテゴリです。 それぞれの瞬間に、特にソフトウェアカウンターによって一意に決定されます。 制御問題を解決するために必要な状態のセットを自分で設定し、必要に応じて、 XまたはYコマンドが到着した場合に次にどの状態になるかを明示的に選択します 。 十分な状態がない場合、必要な数まで任意に増やして、それらの間の接続を明確に規定できます。
正しく理解したい。 プログラムを自動的に実装すると、タイプミスや誤解を免れることもできません。 デバイスを不適切にシミュレートすることで、遷移を間違った状態に設定できますが、これはソフトウェア設計エラーではなく、エンジニアリングエラー、つまり 自動パスまたは非自動パスが選択されているパスとは関係ありません。 非手動の実装では、潜在的な論理エラーの強力なソースが同じモデリングエラーとタイプミスに追加されます。これは、何らかの期待される結果のオーバーレイをもたらす一連のアクションとしての動的プロセスです。
次のパートでは、「ディスプレイ」の例の2つの実装間の競合を調整することにより、実用的なアルゴリズムの強固な基盤に戻ります。一方は自動的に開発され 、もう一方は自動化されません。
推奨文献のリスト。 自動機械について素晴らしい物語があれば、私に書いて、私は付け加えます。
→ 初心者のための、一般に忘れてしまった人のための講義。
→ 強力な講義と例。 パート1
→ 強力な講義と例。 パート2
→ 強力な講義と例。 パート3