
ご存知のように、アメリカの科学者ホイットフィールド・ディフィーとマーティン・ヘルマンによる記事「暗号の新しい方向性」により、1976年に暗号の最後の革命が起こりました。 この作業は、「ビッグバン」としての暗号のその後の開発のためのものでした-非対称暗号の新しい宇宙が誕生しました。 この時点まで(少なくとも公開報道では)対称暗号法しかありませんでした。 若くて未知の科学者は、共通の秘密を開発するために、加入者が最初に秘密鍵を交換する必要がなかったスキームを最初に提案しました。 その根本的な性質に加えて、このアルゴリズムは、そのセキュリティの根底にある「複雑な」タスクが時代遅れになる可能性があるという事実にもかかわらず、それらを新しいタスクに正常に置き換えることができるという点で興味深い。 当初、これは有限体の乗法群(離散対数問題、略称-DLP)の離散対数タスクでしたが、実際には楕円曲線の点群(楕円曲線DLP-ECDLP)の離散対数問題が広く使用されています。 将来(それほど遠くない)、他の「複雑な」問題を使用することになっています。これは、古典的なコンピューターだけでなく、量子コンピューターでも指数関数的に複雑になります。 それらは、量子後と呼ばれます。 これらの問題の1つは、この記事で説明したい楕円曲線間の同質性を見つける問題です。
この記事の目的は、Diffie-Hellmanプロトコル(Diffie-HellmanまたはDH)の新しい数学的な「エンジン」を簡単に説明することであるため、一部の攻撃は考慮されていません。攻撃者はチャネル内のメッセージのみを読み取り、干渉することはできないと想定していますサブスクライバーのメッセージをインターセプトし、独自のメッセージを送信するチャネルの作業(つまり、攻撃者は「中間者」ではありません)。 実際には(たとえば、TLSプロトコルで)、DH公開キーに署名することができ、DHキーを置き換えることができない中間者が既に存在します:サーバーから、DH公開キーは、クライアントからサーバーへの証明書として提供されます-一時(一時)キーが署名されます永久クローズドキーEDSクライアント上。 一般に、厳しい現実では、PKIテクノロジーは、1つのCAに対する両当事者の信頼に基づいて、公開鍵をDHで置き換えることを回避します。 しかし、再び、読者を主要なもの、つまり数学からそらさないために、この記事ではPKIについて何も書きません。 繰り返しますが、システムが実装されて実装された場合、当事者が一時的に(一時的な)公開キーを交換するケースがあります(明らかに、それらを設計した人は忙しすぎて暗号の基礎を学ぶことができない、または少なくとも専門家に頼る)、実際の生活ではこれが必要であることを忘れないでください。 中間者(別名仲介者、別名中間者)はビッグフットではなく、存在します。
過去:クラシックディフィーヘルマン
アリスとボブは、最初にドメインパラメーターを選択します。有限体の乗法グループとgはそのサブグループの生成元です。 ワードジェネレーターに問題はありません。 これは、次のプロパティを持つグループの要素の1つにすぎません。次数を1からグループ内の要素の数までとると、グループ全体が取得されます。 サブグループはグループのサブセットであり、それ自体もグループです(任意の組み合わせで要素を乗算すると、このサブセットの要素のみが取得されます)。
例: 有限体の乗法群です。
グループ要素:
1からp-1までの数字。ここで、pは素数です。
グループ演算a * b mod p:グループaとbの要素を乗算し、a * bをpで除算します。 a * bをpで除算した余りは、演算a * b mod pの結果です。
たとえば、pを11とします。ほとんどの場合、 。 11-1 = 10の要素で構成:1、2、3、4、5、6、7、8、9、10
グループ内の要素の数は、グループ順序と呼ばれます。 ご注文 10に等しい
それでは、操作を少し試してみましょう。
5 * 6 mod 11 = 8
1 * 10 mod 11 = 10
このグループの1は中立的な要素です。 ニュートラル-なぜなら 他の要素と「相互作用しない」ため、操作の結果は常に操作の2番目の要素と等しくなります。 この場合、1 * 10 mod 11は10です。
6 * 2 mod 11 = 1。
任意のグループの任意の要素には、それを中立的な要素に「変える」逆要素があります。 このグループでは、6と2は互いに逆です。
グループ演算が乗算と呼ばれる場合(そうであるように )、そのような表記を逆に使用します アイテム: つまり * = 1このグループについて他に何が言えますか? 可換(またはアーベル)です。
mod p = mod p:aとbの順列から、結果は変わりません。
グループジェネレーターはその要素であり、すべての次数はすべてグループの要素です。 そのような要素が少なくとも1つあるグループは、サイクリックと呼ばれます。 xがジェネレーターであることを理解する方法は? 最も基本的な方法:度xのテーブルを作成します:
度2はどうですか?
2 * 2 mod 11 = 4
4 * 2 mod 11 = 8
8 * 2 mod 11 = 5
5 * 2 mod 11 = 10
10 * 2 mod 11 = 9
9 * 2 mod 11 = 7
7 * 2 mod 11 = 3
3 * 2 mod 11 = 6
6 * 2 mod 11 = 1-サイクルが閉じていることがわかります。 度2はグループ全体を生成します 。
合計:2-ジェネレーター 。
要素の順序は、中立になるために上げる必要がある最小の度合いです。 注文2 10に等しい
次に、次の3度を検討します。
3 * 3 mod 11 = 9
9 * 3 mod 11 = 5
5 * 3 mod 11 = 4
4 * 3 mod 11 = 1
3 5. “” , .. , : , 3, 9, 5, 4, 1.
3?
. , , {3, 9, 5, 4, 1}.
, -: 1. : a*b mod p , {3, 9, 5, 4, 1}.
: 3*4 mod 11 = 1, 9*5 mod 11 = 1, 1*1 mod 11 = 1. ?
2: {1, 10}
{ 1 } {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} (.. )
?
– : “ ”.
x , . , x 1 .
. , 2 5, 10.
2, 2 5!
mod 11 = 4 ≠1
mod 11 = ** mod 11 = mod 11 = 10 ≠1 , , 2 –
4:
4*4 mod 11 = 5 ≠1 ok, 4:
mod 11 = ** 4 mod 11 = 5*5*4 mod 11 = 100 mod 11 = 1 -> 4 – , ? :
18 = 3*3*2. 18: 2, 3, 6, 9 , 3:
3 r1 = 18/3 = 6:
mod 19 = 7 ≠1
3 r2 = 18/2 = 9:
mod 19 = 18 ≠1
.. 2, 3, 6, 9, .. , 1.
, 3, 11, :
mod 19 = 1.
.. 11 3
mod 19 = mod 19 = mod 19
3 {1, 7, 11}
: {1, 18}, {1, 7, 11}, {1, 7, 8, 11, 12, 18}, {1, 4, 5, 6, 7, 9, 11, 16, 17}
DH. – ( ~, . 3072 ) p , (. , 1: mod p=1 ) – (~). – x : mod p.
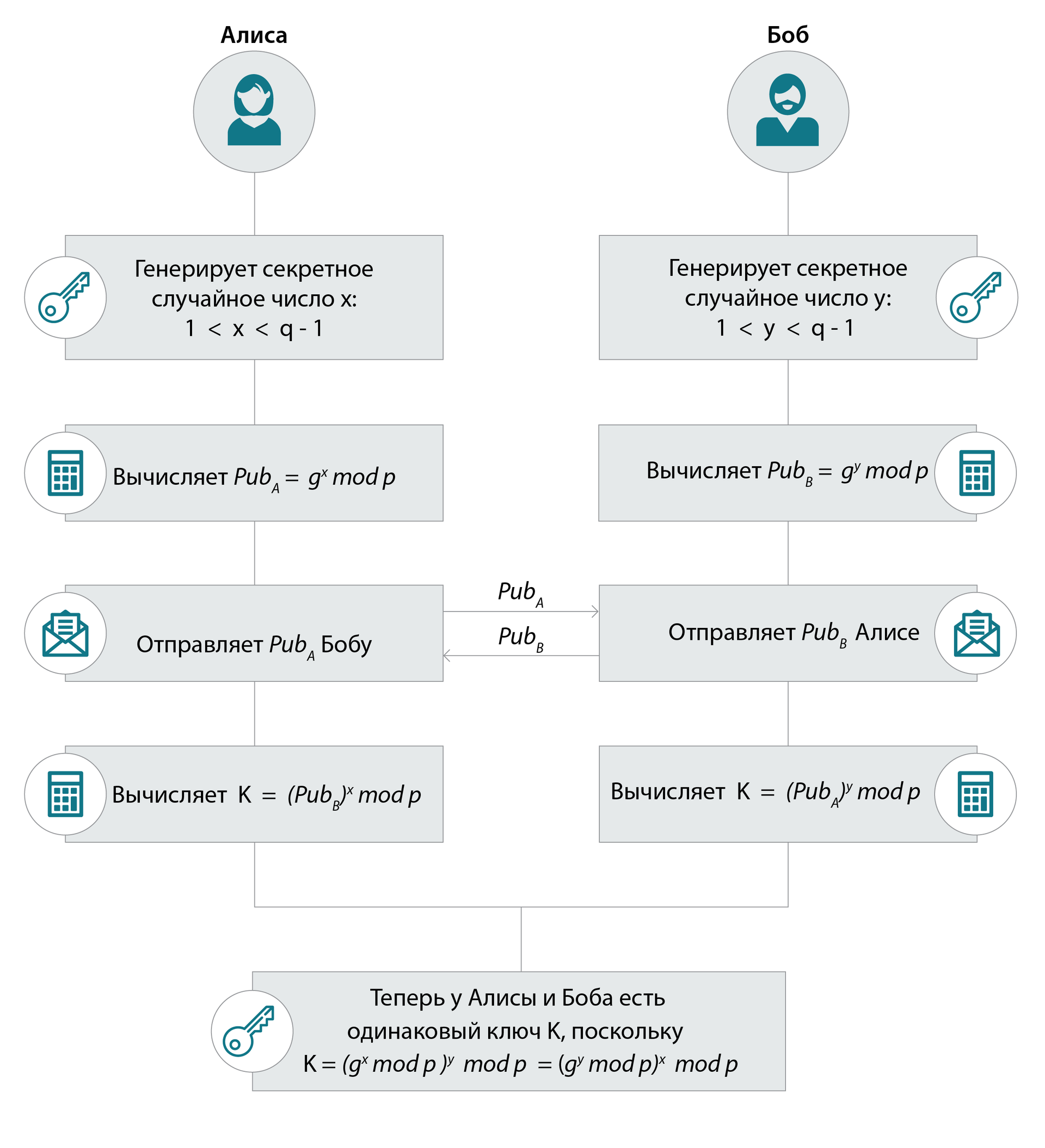
: “” q:
mod p = 1? , .
: , : mod p = 1?
, , , “ ”: ( , ).
, , ( MAC (Message Autentication Code) MAC).
mod p Discrete Logarithm (DL) : p, g . x. , .
, (, , ). , , p ,g . NIST RFC.
DH: “” , .. , .. -, , . , - , DL .
: -
1985 (Neal I. Koblitz) (Victor Saul Miller) , . -, -, MQV, DSS, 34.10-94, . ( ) EC: ECDH, EC ElGamal, ECMQV, ECDSS. 34.10-94 34.10-2001 ( 34.10-2012). ? .
(domain parameters) .
:
1. GF(). C , p —
( )
( n = 1. GF()
(prime field). — 0 p-1)
2. GF() (“ ” ,
( A B) (x y) – ):
= +A+B ( p > 3)
A B , 4+27 ≠ 0, x, y –
3. ( )
#E(GF( ))
q*k, q ( ) – , k –
( ) cofactor ()
4. (base point): Q, q. ( - , , “” . .. . , p-1 , )
:
— , .. (x, y) — . :
(x1, y1) + (x2, y2) = (x3, y3)
(Point At Infinity) ( – , ) O. ( DH): 1*t mod p = t*1 mod p = t, : (x, y) + O= O + (x, y) = (x, y). , - , .. (x, y) , .
GF(p), mod p:
(X1, Y1) (X2, Y2):
X3 = – X1- X2 mod p
Y3 = µ(X1 — X3) — Y1 mod p
µ= (Y2-Y1)/(X2-X1) mod p, X1 ≠ X2:
X1 = X2 Y1 = Y2 ≠ 0, µ= (3+A)/2Y1 mod p
, X1 = X2 Y1 = — Y2 mod p, – .
: , mod p * mod p, —
n Q : [n]*Q.
[n]*Q = Q + Q + … + Q + Q
n ( n ) : Q ( ) n Q: [n]*Q. : n (. ECDLP). ? , Q , [n]*Q Q, [n]*Q. Q .
, ( ). : , , . E GF() #E(GF()). :
#E(GF()) = + 1 – t, t – , t ≤ 2*. .. #E(GF()):
+ 1 – ≤ #E(GF()) ≤ + 1 +
, : . , ? “” – , , . , DLP ( ). . , — . , “” (c q*k, q , k – : 1, 2 4 ) , «» – .
:
NIST P-256 .
: . . q*k, q – , cofactor k = 1. , NIST P-256 .
, ECDLP: ( t , : t mod p = 0) ( t = 1 ). , ECDLP .
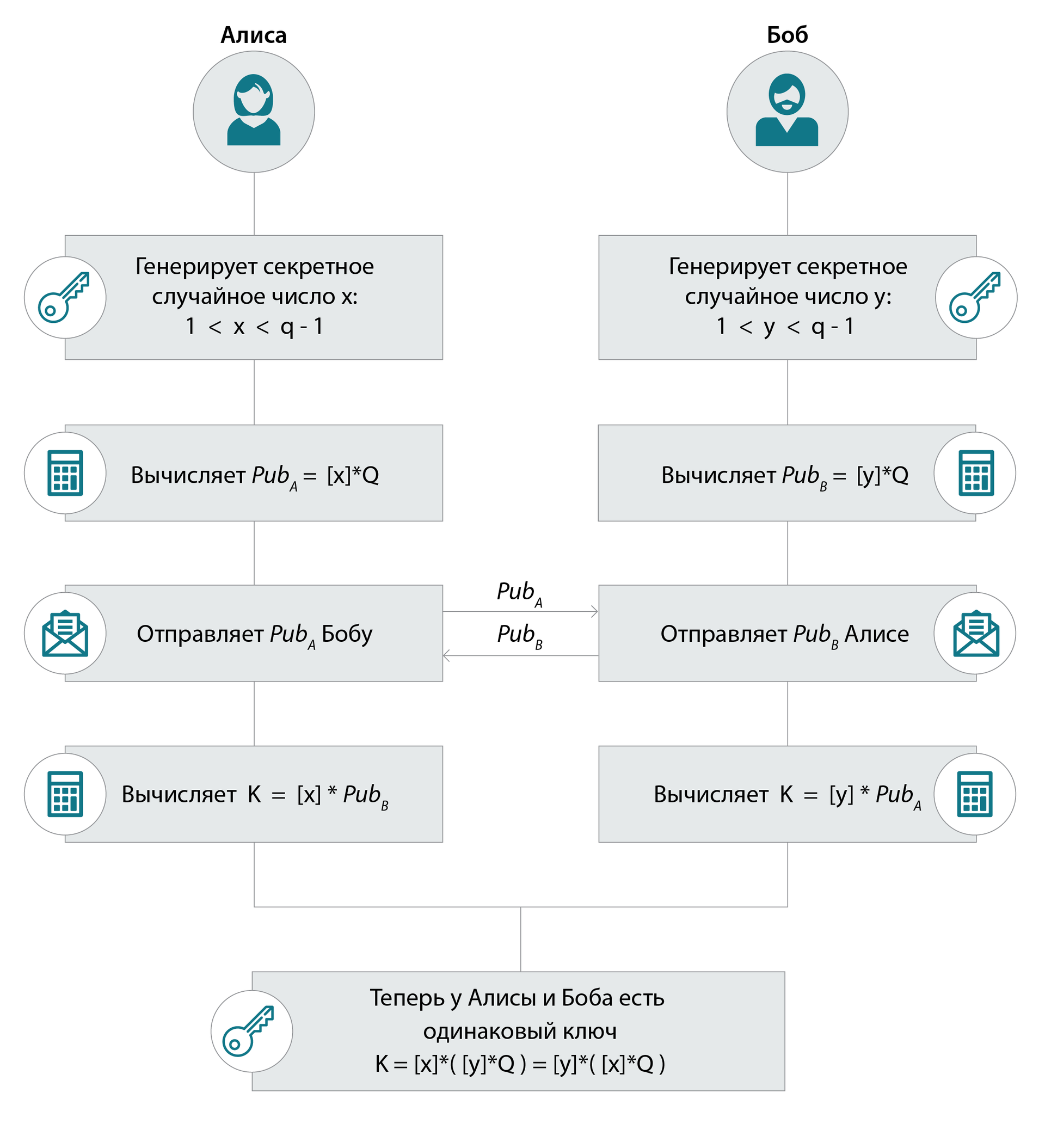
: DH, ( ) , . – . q q. , OK, — - .
:
DH: : , x*y : mod p
opypaste:
DH: : — Q, x*y : [x*y]*Q
( ) ( ). :
: , x*y .
DH : ( ) ECDLP DLP, , , ( ). , RSA: . . – , . , AES c 128 , AES, c 256 ( AES-128 64 , .. ).
, . .
:
, “ ”
Alfred J. Menezes, Paul C. van Oorschot and Scott A. Vanstone “Handbook of Applied Cryptography”
Lawrence C. Washington “Elliptic Curves: Number Theory and Cryptography, Second Edition”