ランダム変数を「聞く」ことを学べば、ランダム変数の分布の法則は「伝える」ことができますか?
確率変数の分布の法則は、測定結果の統計処理において最も「雄弁」です。 測定結果の適切な評価は、測定エラーの動作を決定するルールがわかっている場合にのみ可能です。 これらの規則の基礎は、誤差の分布の法則であり、微分(pdf)または積分(cdf)形式で表すことができます。
分布の法則の主な特徴は次のとおりです。数学的期待値(平均)と呼ばれる測定量の最も可能性の高い値。 標準偏差(std)と呼ばれる数学的期待値の周りのランダム変数の分散の尺度。
追加の特性は、非対称(スキュー)と呼ばれる対称軸に関する分布則の微分形式の混雑の尺度と、尖度と呼ばれる微分形式を包む涼しさの尺度です。 読者は、指定された略語がscipyライブラリから取られていることをすでに推測しています。 使用する統計、numpy。
エントロピーと平均二乗誤差の関係に言及しなければ、測定誤差の分布の法則に関する話は不完全です。 測定の情報理論[1]からの長い説明に読者を煩わせることなく、すぐに結果を定式化します。
情報の観点から見ると、正規分布は均一な分布とまったく同じ量の情報をもたらします。 上記のライブラリの関数を使用してdelta0エラーの式を作成し、ランダム変数xを配布します。
delta0=np.std(x)∗np.sqrt(np.pi∗np.e∗0.5)
これにより、誤差分布の法則を同じ値delta0の一様な法則に置き換えることができます。
別の指標であるエントロピー係数kを導入します。これは正規分布の場合:
k=delta0/np.std(x)=$2.0
正規分布以外の分布はエントロピー係数が低いことに注意してください。
7回読むよりも1回見る方が良い。 一様分布、正規分布、ロジスティック分布の積分分布をさらに比較分析するために、ドキュメント[2]に記載されている例を近代化します。
正規配布のプログラム:
from scipy.stats import norm import matplotlib.pyplot as plt import numpy as np fig, ax = plt.subplots(1, 1) # Calculate a few first moments: mean, var, skew, kurt = norm.stats(moments='mvsk') # Display the probability density function (``pdf``): x = np.linspace(norm.ppf(0.01), norm.ppf(0.99), 100) ax.plot(x, norm.pdf(x), 'r-', lw=5, alpha=0.6, label='norm pdf') ax.plot(x, norm.cdf(x), 'b-', lw=5, alpha=0.6, label='norm cdf') # Check accuracy of ``cdf`` and ``ppf``: vals = norm.ppf([0.001, 0.5, 0.999]) np.allclose([0.001, 0.5, 0.999], norm.cdf(vals)) # True # Generate random numbers: r = norm.rvs(size=1000) # And compare the histogram: ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2) ax.legend(loc='best', frameon=False) plt.show()
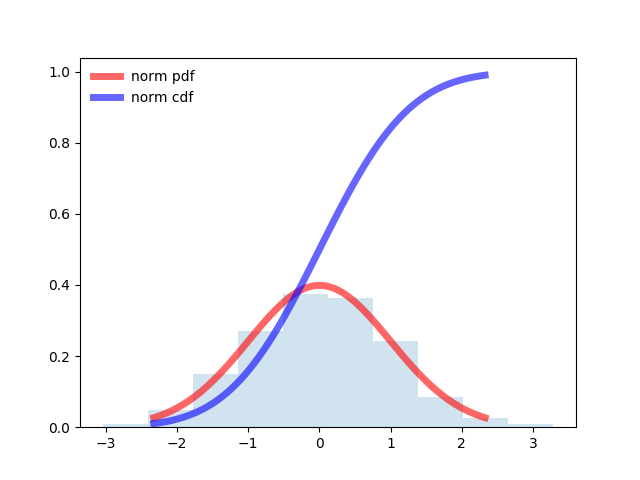
均等配布のためのプログラム:
from scipy.stats import uniform import matplotlib.pyplot as plt import numpy as np fig, ax = plt.subplots(1, 1) # Calculate a few first moments: #mean, var, skew, kurt = uniform.stats(moments='mvsk') # Display the probability density function (``pdf``): x = np.linspace(uniform.ppf(0.01), uniform.ppf(0.99), 100) ax.plot(x, uniform.pdf(x),'r-', lw=5, alpha=0.6, label='uniform pdf') ax.plot(x, uniform.cdf(x),'b-', lw=5, alpha=0.6, label='uniform cdf') # Check accuracy of ``cdf`` and ``ppf``: vals = uniform.ppf([0.001, 0.5, 0.999]) np.allclose([0.001, 0.5, 0.999], uniform.cdf(vals)) # True # Generate random numbers: r = uniform.rvs(size=1000) # And compare the histogram: ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2) ax.legend(loc='best', frameon=False) plt.show()
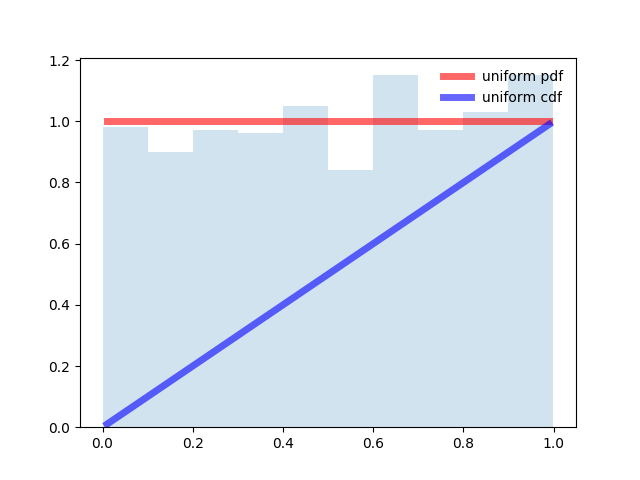
ロジスティック分布のプログラム。
from scipy.stats import logistic import matplotlib.pyplot as plt import numpy as np fig, ax = plt.subplots(1, 1) # Calculate a few first moments: mean, var, skew, kurt = logistic.stats(moments='mvsk') # Display the probability density function (``pdf``): x = np.linspace(logistic.ppf(0.01), logistic.ppf(0.99), 100) ax.plot(x, logistic.pdf(x), 'g-', lw=5, alpha=0.6, label='logistic pdf') ax.plot(x, logistic.cdf(x), 'r-', lw=5, alpha=0.6, label='logistic cdf') vals = logistic.ppf([0.001, 0.5, 0.999]) np.allclose([0.001, 0.5, 0.999], logistic.cdf(vals)) # True # Generate random numbers: r = logistic.rvs(size=1000) # And compare the histogram: ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2) ax.legend(loc='best', frameon=False) plt.show()
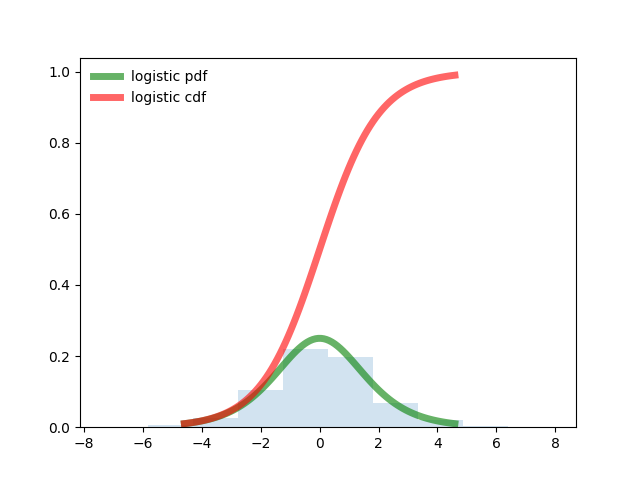
これで、正規法、均一法、ロジスティック法の積分形式がどのように見えるかがわかったので、より一般的な質問-統計サンプルによるランダム変数の分布法の選択-を提起することにより、テスト分布と比較することができます。
テストサンプルの累積確率分布を持つ分布則の選択方法
プログラムの最初の部分を準備し、リストされた積分分布をテストサンプルと比較します。 これを行うために、均一な分布を使用して、分布の法則に共通する基本的なパラメーター、つまり数学的期待値と標準偏差を定義します。
プログラムの最初の部分は、3つの分布法則を積分形式で比較する準備をすることを目的としています。
from scipy.stats import logistic,uniform,norm,pearsonr from numpy import sqrt,pi,e import numpy as np import matplotlib.pyplot as plt fig, ax = plt.subplots(1, 1) n=1000# x=uniform.rvs(loc=0, scale=150, size=n)# x.sort()# print(" ( ) -%s"%str(round(np.mean(x),3))) print(" ( ) -%s"%str(round(np.std(x),3))) print(" -%s"%str(round(np.std(x)*sqrt(np.pi*np.e*0.5),3))) pu=uniform.cdf(x/(np.max(x)))# ax.plot(x,pu, lw=5, alpha=0.6, label='uniform cdf') pn=norm.cdf(x, np.mean(x), np.std(x))# ax.plot(x,pn, lw=5, alpha=0.6, label='norm cdf') pl=logistic.cdf(x, np.mean(x), np.std(x))# ax.plot(x,pl, lw=5, alpha=0.6, label='logistic cdf')
以下、比較の結果は、計算の過程を制御するために印刷機能に導入されます。
テストの積分分布と比較結果は、プログラムの2番目の部分に示されています。 テストと3つの積分分布則のそれぞれの間の相関係数を決定します。
相関係数はわずかに異なる場合があるため、発表された偏差二乗の追加定義が導入されています。
プログラムの第二部
p=np.arange(0,n,1)/n ax.plot(x,p, lw=5, alpha=0.6, label='test') ax.legend(loc='best', frameon=False) plt.show() print(" - %s"%str(round(pearsonr(pn,p)[0],3))) print(" - %s"%str(round(pearsonr(pl,p)[0],3))) print(" - %s"%str(round(pearsonr(pu,p)[0],3))) print(' -%i'%round(n*sum(((pn-p)/pn)**2))) print(' -%i'%round(n*sum(((pl-p)/pl)**2))) print(' -%i'%round(n*sum(((pu-p)/pu)**2)))
分布形式の積分形式のテスト関数は、段階的累積–0 + 1 / n + 2 / n +……+ 1の形式で構築されます。
ロボットプログラムのスケジュールと結果。
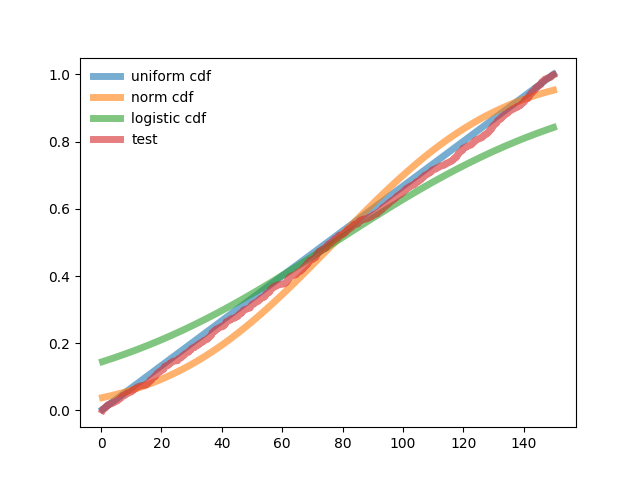
サンプルでの数学的期待値(分布の比較に共通) -77.3
サンプリングエラー (比較された分布に共通) -43.318
エラーのエントロピー値は89.511です
正規分布とテスト分布の相関は0.994です
ロジスティック分布とテスト分布の相関-0.998
均一分布とテスト分布の相関-1.0
テストからの正規分布の偏差の二乗の加重合計は37082です。
テストからのロジスティック分布の偏差の加重平方和-75458
テストからの均一分布の偏差の平方和の加重合計-6622
積分形式のテスト確率分布は均一です。 一様分布の相関係数の差が最小であるため、テストからの加重偏差は通常の偏差の5.6倍、ロジスティックの偏差の11倍です。
おわりに
統計的サンプルのデータに応じたランダム変数の分布の法則の選択の所定の実装は、おそらく同様の問題を解決するのに役立つでしょう。
1. 測定の情報理論の要素。
2. 統計関数。