M *-スマートフォンでの全世界にわたる最短経路検索アルゴリズム

大きなグラフで最短経路を検索する場合、従来のコスト見積もりはうまく機能しません。 データは明らかにメモリに収まらず、総コストは表示されるエッジの数よりもディスクアクセスの数に大きく依存します。 また、ディスク操作の数は非常に主観的な要因であり、特定のアルゴリズムにとって便利な形式でディスクに保存されるグラフの形式的に困難な適合性に依存します。 さらに、コンパクト性が非常に重要になります-エッジと頂点ごとの情報量。



猫の下では、A *アルゴリズムの一般化されたヒューリスティックが提示されます。これは、たとえば携帯電話など、リソースが限られている大きなグラフでの実用的な適合性に照らして正確に役立ちます。



したがって、私たちのタスクは、ポイントからポイントへのグラフに沿った最短経路を構築することです。 同時に、グラフは十分に大きいため、メモリ内に完全に保持することはできません。また、多数の頂点について計算することもできません。 優れた例は、OSMロードグラフです。 現時点では、 OSMのピークの数は46億を超えており 、オブジェクトの総数は4億です。



このような条件では、中間データを保存するために必要なメモリ量がないため、純粋なダイクストラまたはレビティック アルゴリズムによる多かれ少なかれ拡張されたルートの検索が不可能であることは明らかです。



ダイクストラのアルゴリズムは何をしますか？

1. ゼロコストで出発点を優先します。
2. キューに何かがありますが、頂点Vを、これまで見ていない各出力エッジ（E）に対応させます。
   
   
   1. これが目的のエッジではないことを確認し、そうである場合は終了です。
   2. 通路Eのコストを計算します。
   3. そして、エッジEの終了頂点を、それを達成するためのコスト（Vを達成するためのコスト+ Eのコスト）とともにキューに入れます。

その結果、スパース（たとえば、幾何学）グラフの場合、値O（n * log（n）+ m * log（n））を取得します。ここで、nはスキャンされた頂点の数、mはスキャンされたエッジの数です。







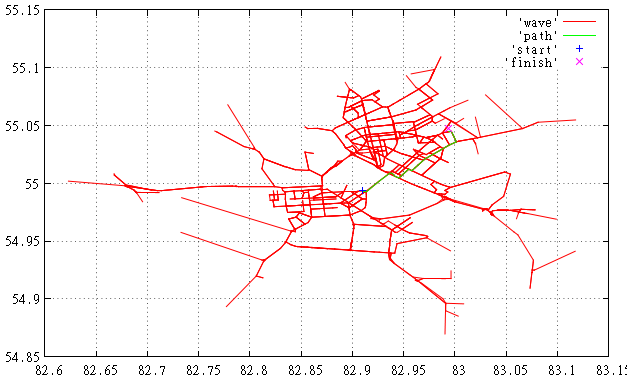
図1ここでは、見つかったルートとそれとともに表示されるリブが表示されます。



問題は、ダイクストラのアルゴリズムがグラフのプロパティと目的のルートに関する情報を一切使用せず、その操作中（いわゆる「波」の伝播）に、この「波」の周囲が区別なくすべての方向に目的のポイントから移動することです。



一方、たとえば開発された道路網のような幾何学的なグラフでは、「波」の広がりをターゲットに向けて刺激し、他の方向では細かくするのが理にかなっています。 このアイデアは、ダイクストラのアルゴリズムの一般化であるA *アルゴリズムで実装されています。



A *では、頂点を優先キューに配置する際の頂点のコストは移動距離に等しいだけでなく、残りのパスの推定値も含まれます。 この評価を取得するにはどうすればよいですか？



これはかなり計算上安価な推定値である必要があることに注意してください。 何度も実行されます。 最初に頭に浮かぶのは、現在のポイントからフィニッシュラインまでの幾何学的な距離を計算して、これから進むことです。たとえば、左に10 km-都市を移動するときの平均速度は20 km / hであるため、推定は30分です。



さらに、エッジがフィニッシュラインに向かっている場合、そのスコアは減少し、移動距離を補正します。



ターゲットからのエッジの場合、この推定値は大きくなり、その結果、そのようなポイントは大きな重みでキューに落ち、到達しない可能性があります。



ところで、優先度キューのサイズが強制的に制限され、ヒューリスティックの観点から「価値のない」候補が単純に破棄されるビーム検索技術を使用して、ほぼ同じ効果を達成できます。







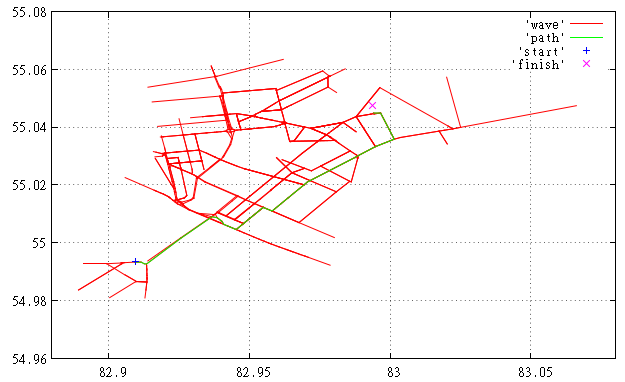
図2ここでは、説明したヒューリスティックを使用して同じルートを検索し、違いを感じています。



コスト推定値が0を返す場合、パスの残りの部分が無限の速度で突進すると思われるかのように、A *はダイクストラのアルゴリズムになります。



*は、いわゆる 情報に基づいたアルゴリズム ヒューリスティックでは、目標の方向への移動が成功につながる可能性が高いという仮定を使用します。



評価関数のプロパティは何ですか？ それは信じられなければなりません。 すでにわかっているように、過度に楽観的な評価は、グラフの表示部分を減らす試みを否定します。 一方、悲観的すぎる評価は、アルゴリズムが何であれ、厳密にその方向にパスを構築することを強制します。 これは私たちに合わないでしょう。



現実的な評価は、グラフのプロパティ、できればデータモデルに基づいて行う必要があります。 たとえば、この時刻の混雑のレベルとグラフのトランスポート接続のレベルから計算されます。 たとえば、川のない都市では、 マンハッタン距離がうまく機能します。



しかし、ここにはすぐに多くのニュアンスがあります。

• 私たちが街にいることをどのように判断しますか？ これはそれほど安くはありません。
• しかし、ほとんどの都市が川の上に建てられたことは何もありませんか？
• 市内では、道路のさまざまなセクションを非常に異なる方法でロードできます。
• そして、私たちが多くの都市や川を走らなければならないのであれば？

branch and boundメソッドの精神で異なるヒューリスティックを使用できます。

1. 非常に悲観的なヒューリスティックを備えたパスを見つけます。そこから、おそらくより効率的なルートが存在することになります。
2. ここで、上からの推定値として見つかったルートのコストを使用します。すでに見つかったよりも効率的なルートを明らかにできない申請者を優先順位に含めないだけです。
3. アセスメントの悲観性を減らし、コストの上限を設定したルートを再度作成します。
4. 新しい評価を取得します。
5. 満足のいく解決策が得られるまでこれを続けます。

コスト見積もりには別の問題がありますが、これは無視できません。



人生では、幾何学的に近いオブジェクトは、道路グラフの視点からかなり離れている場合があります。 たとえば、川、山脈、海の異なる側にいる場合...この場合、幾何学的な近接性に基づいた推定は、「波」を頑固に間違った方向に向けることで状況を悪化させ始めます。







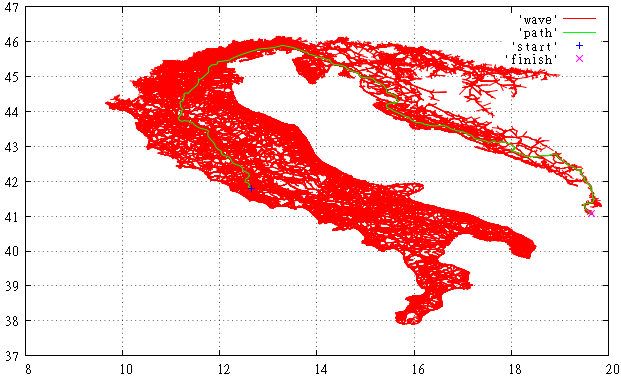
図3これは、OSMグラフのスキャンされたA *部分がイタリアからアルバニアへの道を見つけるために見えるものです。



ただし、これはダイクストラのアルゴリズムよりも優れています。 イタリア全体を埋め尽くす「波」が溢れ出し、速度を増し、すぐに目標に到達したことがはっきりとわかります。







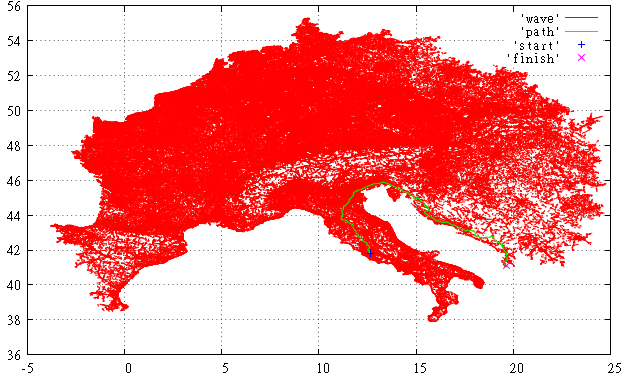
図4そして、これがダイクストラアルゴリズムのグラフのスキャンされた部分です。 彼女と比較すると、それほど悲観的ではありません。



どういうわけかアルゴリズムを改善することは可能ですか、コンピューターサイエンスはこれについて何と言っていますか？



双方向検索



2つのA *波を互いに向かって発射できます。 これは双方向検索と呼ばれ、一見非常に魅力的なアイデアのようです。 実際、輸送の接続が良好な場合、「波」は楕円体であり、互いに向かって発射される2つの小さな波は、1つの大きな波に比べて小さな領域に気づきます。 一方、「波」の遭遇を検出する問題が発生し、その周囲には非常に多くのポイントが存在する可能性があり、すべてのステップでエイリアンの周囲のエッジの存在を確認するのはそれほど安くはありません。







図5ダイクストラの近づいてくる波



おそらく、これは、表示されたグラフの一部のボリュームの実際のゲインと一致する可能性があります。 しかし、イタリアからアルバニアへの旅行を見つける上記の例を見ると、双方向検索は役に立たず、状況を悪化させるだけであることがわかります。 イタリア全土を注ぐことに加えて、波が出会う前にギリシャ全土とバルカン半島を見るように強制されます。 障害物に寄りかかった1つの「波」の代わりに、2つの波があります。

階層的アプローチ

道路階層を使用する



StreetMap USAなどの一部の商用システムでは、適切に計画された道路網にはルーティングの2つのレベルの性質があるという事実を使用します。ローカル道路のネットワークと、長距離を移動する（はるかに小さい）高速道路ネットワークがあります。 この事実を使用するのは自然に思えます。 ゲートウェイが導入されます（トランジットノード）-あるレベルから別のレベルへのトランジションが発生するピーク。 「かなり長い」パスを見つけることは、以下からパスを見つけることになります。

• いくつかの最も近いゲートウェイへの出発点。
• 最終地点に最も近いいくつかのゲートウェイ。
• 最初のゲートウェイから最後のゲートウェイまでの最短ルートは、もちろん1つのセッションで行われます。

6スライスストリートマップ



このアプローチの利点は明らかです。 短所は次のとおりです。

• 道路網がどこでもうまく計画されているわけではなく、一部の場所では自発的に成長しているため、元のメッセージは機能しません。
• 最上位ネットワークを接続して検証する必要があります。 たとえば、OSMからは、クラスごとに道路をフィルタリングするだけでは、そのようなネットワークを（手首を軽く振って）取得することはできません。
• Gateway Instituteでは、多くの手作業も必要です。

グラフ階層の構築



グラフを調整する可能性や希望がない場合、階層を自動的に構築する機会が残ります。



いずれにしても、グラフは検証されませんが、エッジの属性により許容可能な品質のルートを構築できるという考えが活用されています。 ただし、グラフのサイズが原因で、同じA *を操作モードで構築すると、法外な費用がかかります。



たとえば、次のようになります。

• 事前計算段階では、（ランダムな）頂点のセットが選択されます。
• 通常のA *を持つ空間的に離れた頂点のペアの場合、最短ルートが構築されます。
• 構築されたルートに基づいて、渡されたrib骨の統計が保持されます。
• 十分な量のデータが蓄積されると、訪問先のエッジが階層の次のレベルとして宣言されます。
• 分岐のない連続したrib骨は、運賃を維持しながら「マクロrib骨」に統合されます。

構築されたグラフは、ここで説明した手順の対象になる場合があるため、必要な数の階層が構築されます。



このような階層グラフでのルーティングは、双方向検索（A *またはダイクストラのアルゴリズム）によって実行されます。



セパレーター



このメソッドの主なアイデアは、エッジの小さな部分（セパレーター）を削除することにより、グラフをコンポーネントに分割する試みです。 これらのセパレータとそれらの間の事前に計算されたパスは、次の階層を形成します。 [1] O（n * log（n）** 3）時間と予備計算のためのディスク容量を費やしたため、O（sqrt（n）* log（n））でクエリを実行することが可能であると述べられています



グリッドベースのトランジットノード



これは一般にセパレーターと同じ考え方ですが、スケーリングと単純化のために、グラフはラティスまたはクワッドツリーによってフラグメントに分割され、フラグメントの境界と交差するエッジは一時的になります。 これの価格が効率であることは明らかです。 プラスは高度な自動化であり、その結果、人的要因が欠如しています。



距離表



階層の上位レベルでは、検索プロセスでパスが検索されず、通過ノード間の距離の事前計算済みテーブルに基づいてコストが計算されます。 ルートが定義されると、パスはローカル検索によって復元されます。







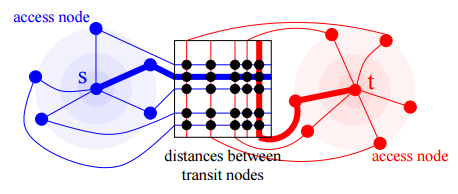
図7 [1]



リーチ [3]



この方法の考え方は次のとおりです。長い最適ルートを構築する場合、「ローカル」エッジはルートの最初または最後にのみアクセスされることに気付きました。 したがって、多くの「トレーニング」長いルートを構築したことで、ルートの端に1つまたは別のエッジがどれだけ近いかを理解できます。



一部のトレーニングルートP（s ... ..uv ... ... t）については、インジケーターリーチが導入されます-エンドリーチ（uv）の最小距離= min（dist（s ... ..u）、dist（v ... ..t）） 。

トレーニングセット全体で、リーチ（uv）は、エッジ（uv）に遭遇するすべてのルートの最大値です。



「戦闘」検索では、開始と終了から遠く離れた小さなリーチ値を持つエッジを避けようとします。







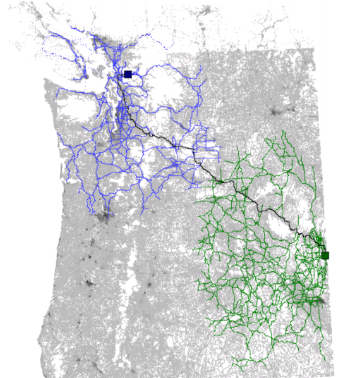
図[21]



この方法のアイデアは非常に美しく、トレーニングサンプルの品質、その妥当性、およびトレーニングに費やされたリソースによってのみ疑問が生じます。

目的のあるアルゴリズム

アークフラグ [4]



グラフはフラグメントに分割されます。 事前に定義されたポイント間の最短ルートの構築に関するトレーニングが実施されています。 トレーニングパスを構築する場合、エッジごとに、最終ポイントのセルへの最短ルートがパスを通過するという事実が残ります。



したがって、各エッジに対して、フラグのマスクを保存します。グラフのフラグメントには、最短でこのエッジを介して到達できます。



この方法の特定の欠点は肉眼で確認できます。

• グラフのフラグメントの数を大きくすることはできません。8Kのフラグメント（それほど多くはありません）は、エッジごとに（おそらく圧縮不可能な）キロバイトを与えます。 シック！
• フラグメントのスライスには細心の注意を払う必要があり、フラグメント内でグラフを接続する必要があります。

ALT [5]



すべての頂点から、少数のランドマークが選択されます：λ。 初期バージョンでは、各頂点について、各λまでの値が以前に計算されていました。 これには膨大な量の追加メモリが必要でしたが、後に要件が緩和され、ピークがグループ化され始めました。



ALTでの検索はA *のように実行されますが、残りのパスの推定は計算されたコストに基づいて行われます。 ターゲット頂点tに向かう途中のエッジ（u、v）を考えてみましょう。 各λについて、三角形の不等式に従って、パスの残りの部分の推定値（λを使用）があります：dist（λ、t）-dist（λ、v）≤dist（v、t）およびdist（v、λ）-dist（t 、λ）≤dist（v、t）。 すべてのλの最小値により、希望する推定値が得られます。







図9

予備結果

開発が進行している主な分野は2つあります。

1. 階層。 これらは、構造化されたグラフで長距離にわたる非常に効率的なパスの構築を可能にします。 しかし、近距離では、通常のA *またはダイクストロイを使用する方が安価です。 したがって、両方のアルゴリズムが平凡に機能する「灰色」の領域があります。
   
   
   
   さらに、アモルファスグラフでは、階層を構築しようとしても問題が発生するだけです。 同等の道路の長方形格子の形のグラフを想像してください。 特定の方向に移動する場合、正しい解決策は、方向に関連付けられた確率でランダムな方向に回転することです。 つまり ターゲットへの方位角が45°の場合、渋滞が発生しないように左右に曲がる可能性が等しくなります。
   
   
   
   このようなグリッドに階層を構築しようとすると、道路網が非効率的に使用されるという事実につながります。
   
   
   
   
2. グラフの本質的な性質を使用して、目標に向かって移動する方向について決定を下します。 このアイデアは有望に見えますが、多くの疑問が生じます。 主な問題は人的要因です。 ランマークを使用すると、Arc-Flagsの断片には専門家の参加が必要になります。その定義が偶然に委ねられている場合、医師が処方したものを簡単に入手できます。
   
   
   
   さらに、追加のメモリが必要です（グラフサイズが非線形）。
   
   

「ニカノール・イバノビッチの唇をイヴァン・クズミッチの鼻に当てて、バルタザール・バルタザロビッチのようなsw歩をするなら、おそらく...」©



公平に言えば、このような試みは数多くあり、そのうちのいくつかはこの記事の出典のリストに記載されていると言う価値があります。 しかし、もちろん、私たちは自分自身を変えず、独自の「比類のない」方法を思いつきます。 ️

発見的

地理座標に基づいてある地点から別の地点へのパスのコストを推定するための単純で安価な（計算上および追加の情報の観点から）ヒューリスティックを開発するタスクを設定します。 直接距離が合わない、それは非常に間違っている可能性があり、ジブラルタルとタンジールを見てください。



アイデアはこの仕事に戻ります。

• OSMで作業しているため、グラフのスケールは惑星全体です。
• 1°のグリッドで空間を分割します。はい、それは極に歪みを与えますが、推定値を作成しているだけです。
• グラフを作成するとき、このグリッド上のパスをラスタライズします。たとえば、ノボシビルスクの2番目のクルプスカヤレーンでは、55°Nに対応するボックスにマークを付ける必要があります。 および82°東
• 知っているすべての道路をラスタライズした後、ある程度正確な人口マップを取得します。
  
  
  
  
  
  
  
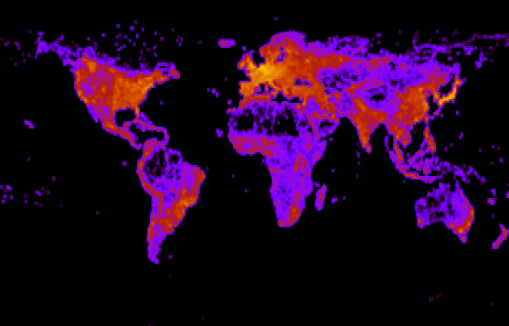
  図10-対数目盛の1平方度あたりの道路の数
  
  
  
  
• マップは、人口密集したセルが頂点であるグラフと見なします。
• 隣接するセルにデータが入力されている場合、これがエッジであり、運転可能な別のセルから、赤道で直行料金が111 kmで、料金に2のルートが斜めに掛けられていると仮定します。
• このグラフで、ダイクストラのアルゴリズムに従ってウェーブを開始し、各頂点に到達するコストを覚えていれば、到達可能なポイントでフィニッシュラインまでのパスのコストを推定できます。 たとえば、ノボシビルスクから波を開始すると、次のようになります。
  
  
  
  
  
  
  
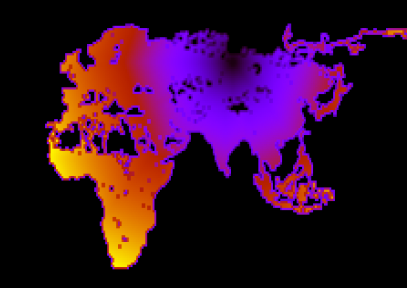
  11 Nskからの運賃の見積もりは、オレンジに近いほど、経路が長くなります。
  
  

検索のために：

• 表面の1平方度あたりのビットごとにのみ保存します。
• このビットマップで最終ポイントのウェーブを開始したら。
• 座標を知っているグラフの頂点については、一定の時間、この地点から終点までの運賃の見積もりを取得します。

しかし、程度はかなり粗いグリッドであり、たとえば、ノルマンディーとの「小さな島」のように、いくつかの海峡は互いにくっついています。



OSMにはタイプがあります-海岸線です。 海岸線をラスタライズし、沿岸とマークされたセルから「本土」のセルにのみ移動できるようにします。





図12海岸線OSM



しかし、ここでは次のことがわかります。

• どこにも海岸線はありません。
• 日本などはすべて沿岸のセルで構成されています。
• ジブラルタルとタンジールは同じケージに入れられました。
• ...

わかりました。重要な海峡に分割線を手で描き、ラスタライズして、波が伝播するときに交差することを禁止する必要があります。



幸いなことに、これは一度きりの仕事であり、そのような海峡はあまりありません。



ここでは、例えば、イタリアからの「波」の広がり、ジブラルタル海峡に注意を払っています。







図13イタリアへの旅費の見積もり、オレンジに近いほど、経路は長くなります。



一般に、スキームは受け入れられますが、次のとおりです。

1. 手作業が必要です。
2. 多くの手作業があります。
3. 複数の分割線が1つのセルにある場合は、非常に注意する必要があります。

おそらくここでは、各「沿岸」セルがクアッドツリーで表される場合にオプションがうまく機能します。波の伝播もクアッドツリーの要素に沿って実行する必要があります。



しかし、それでも、これらすべてにストレッチがあるため、プランBが登場します。

プランB

1. たとえば、「グラフの階層を構築する」セクションで説明した方法で取得した、グラフの上位階層があるとします。
2. このレベルは十分に粗いため、任意の距離での検索は問題になりません。
3. したがって、グラフ階層の上位レベルに構築されたパスを手にしています。
   
   
   
   
   
   
   
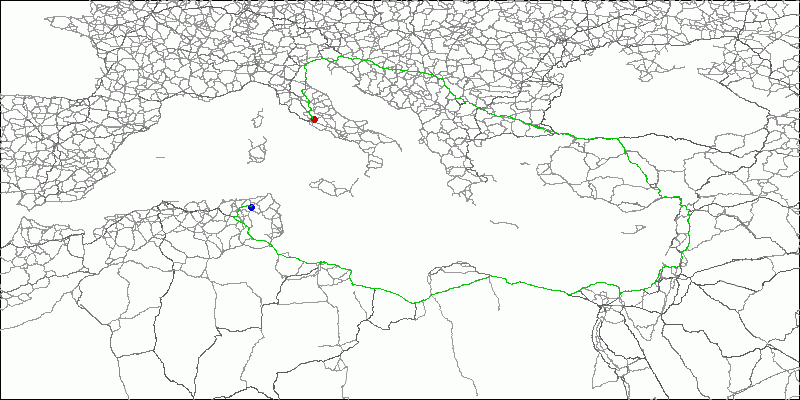
   図14上のレベルのグラフに沿って配置されたパス。
   
   
   
   
4. もちろん、フィニッシュを含む500 kmごとに、このルートに基準点を描画します
   
   
   
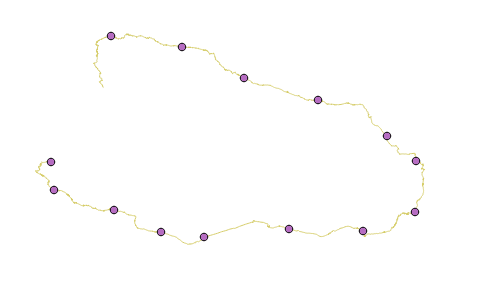
   図15参照ポイント。
   
   
5. 各基準点について、そこからフィニッシュラインまでの残りの部分を知っています。 これで、A *の残りのヒューリスティックは2つの部分で構成されます。
   
   
   1. 現在の基準点までの幾何学的距離。
   2. 現在の基準点からフィニッシュまでの残りのパス。
6. 検索の開始時に、最初の参照点が現在の参照点に割り当てられます。 200 km（条件付きで）に近い幾何学的距離で（もちろん、条件付きで）アプローチすると、次の基準点に焦点を合わせ始めます。 など、フィニッシュラインまで。
7. 結果は次のとおりです。
   
   
   
   
   
   
   
   同じく図。 11サポートパスが急激に方向を変えると、波が広がり始める様子をはっきりと見ることができます。 ただし、読み取られるデータの合計量は非常に少なくなります。 〜20倍の加速も観察されます。
   
   
   
   
8. 何よりも、この手法はヘッダーからこの記事までの画像に似ています。 したがって、著者は彼女にM *という名前を付けました（「M」は「ニンジン」を意味します）。

結論



そのため、読者には、A *の残りのパスのコストを計算するヒューリスティックの2つのオプションが提示されます。



両方のオプション：

• 実際にパフォーマンスをテストしました。
• A *の速度はほぼ同じです。指定されたパスの場合、データの読み取りと解凍を行う4.5秒（通常のデスクトップ）、0.5秒-加熱されたキャッシュ上のウェーブの通過のみです。
• 追加で保存される情報の量は最小限です-2番目のオプションでは0.2％、最初のオプションではさらに少なくなります。
• なぜなら *は元のグラフで機能し、フェリー、跳ね橋、交通データなど、時間制限の使用に障害はありません...

それはそうかもしれませんが、これは別のグラフ作成ツールであり、リソースが限られている場合やデータが無制限の場合に非常に便利です。 特に、両面検索に同じ手法を使用することを禁止する人はいません。





PS ： DUMP 2017でのレポートの結果に関する記事