テンソルフローを使用した機械学習の概要

次の5年間で、1人の知的能力を備えた機械を構築する場合、その後継者は、すべての人類を組み合わせたものよりもすでに賢くなります。 1、2世代後、彼らは単に私たちに注意を向けなくなります。 あなたがあなたの庭の蟻に注意を払わないように。 あなたはそれらを破壊しませんが、あなたはそれらを飼いならしません、彼らはあなたの日常生活にほとんど影響を与えませんが、彼らはそこにいます。

セス・ショスタク

はじめに

一連の記事は、ニューラルネットワークに精通することを決めたときに見たいものの拡張版です。 主に、テンソルフローとニューラルネットワークに精通したいプログラマ向けに設計されています。 幸運にも不幸にも私にはわかりませんが、このトピックは非常に広大なので、最も有益な説明でも大量のテキストが必要です。 したがって、ストーリーを4つの部分に分けることにしました。

1. はじめに、テンソルフローと基本的なアルゴリズムに精通している（この記事）
2. 最初のニューラルネットワーク
3. 畳み込みニューラルネットワーク
4. リカレントニューラルネットワーク

以下に示す最初の部分は、テンソルフローを使用する基本を説明すると同時に、機械学習が原理的にどのように機能するかを、テンソルフォールを例として説明することを目的としています。 第2部では、最終的にニューラルネットワークの設計とトレーニングを開始します。 多層化され、トレーニングデータの準備とハイパーパラメータの選択のニュアンスに注意を払ってください。 畳み込みネットワークは現在非常に人気があるため、3番目の部分は、その作業の詳細な説明に割り当てられています。 さて、最後の部分では、リカレントモデルに関するストーリーが計画されています。私の意見では、これは最も困難で興味深いトピックです。

テンソルフローをインストールする

テンソルフローのインストールプロセスの説明はこの記事の目的ではありませんが、64ビットWindowsシステム用のCPUバージョンのインストールプロセスと、後で使用するアドオンについて簡単に説明します。 一般的に、インストール手順はtensorflow Webサイトで見ることができます。

1. Pythonバージョン3.5をダウンロードしてインストールします*（ 3.5.3執筆時点での最新バージョン ）。 インストール中に、「Python 3.5をPATHに追加」ボックスをチェックします。 たとえば、異なるバージョンのインタープリターを積極的に使用しているために、このバージョンのpythonのディレクトリを環境変数に追加したくない場合は、指定された配布バージョンのスクリプトフォルダーから以下の手順に従う必要があります（cd "path to python 3.5 / Scripts"）。
   
   
   
   
2. インストール後、コマンドラインを実行します（インストール後、PythonディレクトリはPATH環境変数に移動しません）。
   
   
   
   
3. 次に、コマンドを実行します。
   
   
   
   
   1. pipの更新：「pip install --upgrade pip」
   2. setuptoolsの更新：「pip install -U pip setuptools」
   3. CPUの下にtensorflow 1.0.1をインストールする：「pip install --ignore-installed --upgrade ci.tensorflow.org/view/Nightly/job/nightly-win/DEVICE=cpu、OS = windows / lastSuccessfulBuild / artifact / cmake_build / tf_python /dist/tensorflow-1.0.1-cp35-cp35m-win_amd64.whl»
   4. matplotlibのインストール（グラフ用）：「pip install matplotlib」
   5. Jupyterのインストール：「pip install jupyter」
      
      
4. インストールが完了したら、Jupyterを起動し、コマンド「jupyter notebook」を実行します。開いたタブで、ipynbバージョンの記事を開くことができます（ こちらをご覧ください ）。

以下にvbsのスクリプトを示します。詳細を説明せずに必要なソフトウェアをすべてすばやくインストールしたい場合は、それを実行して指示に従ってください。

テンソルフローの紹介

テンソルフローを使用する原理は非常に簡単です。 操作のグラフを作成してから、このグラフにデータを転送し、計算を実行するコマンドを提供する必要があります。 以下の図では、このようなグラフの3つの例を見ることができます。



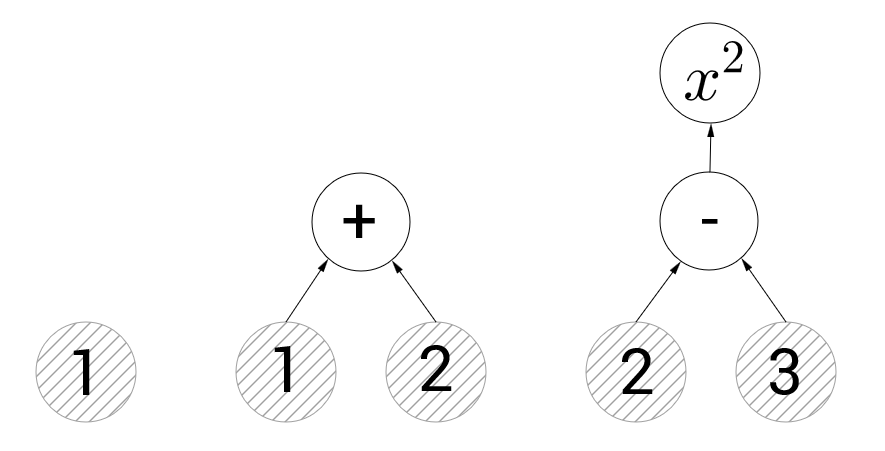
左側のグラフには、値1の定数を表す1つの頂点のみが含まれます。以降、このような図では、定数を持つ頂点は灰色のハッチング付きの円で示され、ハッチングなしの操作がある頂点は示されます。 中央のグラフは、加算操作を示しています。 tensorflowに加算操作を表す頂点の値を計算するように要求すると、それに向けられたグラフのエッジの値を計算し、それらを合計します（つまり、3が返されます）。 右のグラフには、減算と2乗の2つの操作の頂点があります。 二乗を表す頂点を計算しようとすると、テンソルフローは最初に減算します。 計算グラフの概念は問題を引き起こさないと思います。



空のグラフはtf.Graph（）関数で作成できます。さらに、ライブラリが接続されるとデフォルトでグラフが作成されます。グラフを明示的に指定しない場合は、グラフが使用されます。 以下の例は、2つの異なるグラフで2つの定数を作成する方法を示しています。

 import tensorflow as tf #       #   -   default_graph = tf.get_default_graph() #     - c1 = tf.constant(1.0) #    second_graph = tf.Graph() with second_graph.as_default(): #         c2 = tf.constant(101.0) print(c2.graph is second_graph, c1.graph is second_graph) # True, False print(c2.graph is default_graph, c1.graph is default_graph) # False, True
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

データ転送と操作はセッションで発生します。 セッションはtf.Sessionを呼び出すことで開始され、セッションオブジェクトでcloseメソッドを呼び出すことで終了します。 セッションを自動的に閉じるwithコンストラクトを使用できます。

 default_graph = tf.get_default_graph() c1 = tf.constant(1.0) second_graph = tf.Graph() with second_graph.as_default(): c2 = tf.constant(101.0) session = tf.Session() #     - print(c1.eval(session=session)) # print(c2.eval(session=session)) #  ,    session.close() #  : with tf.Session() as session: print(c1.eval()) #       eval #   : with tf.Session(graph=second_graph) as session: print(c2.eval()) #       eval #: # 1.0 # 1.0 # 101.0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

一般的なグラフとセッションが明確であり、それらの機能がここで詳細に議論されないことを願っています。これらのメカニズムを徹底的に分析したい人は、ドキュメントを直接知ってください。 次に、グラフの作成に進みます。 前の例では、グラフに定数が追加されましたが、それが何であり、プレースホルダーや変数とどのように異なるかを調べる時が来ました。 以下の例では、式を表すより複雑なグラフが作成されます $$ $インライン$ a \ cdot x + b $インライン$ 。

 #   a.           #       ,      : # a = tf.constant(2.0) #  : # value ( ) -   # shape - . : [] - , [5] -   5 , [2, 3] -  2x3(2   3 ) # dtype -   ,     https://www.tensorflow.org/api_docs/python/tf/DType # name -  .            a = tf.constant(2.0, shape=[], dtype=tf.float32, name="a") #   x #         #       ,    : # initial_value -     # dtype - , name - ,     x = tf.Variable(initial_value=3.0, dtype=tf.float32) #           ,      #       placeholder #          ,     #       b = tf.placeholder(tf.float32, shape=[]) #     ,        f = tf.add(tf.multiply(a, x), b) #     f = a*x + b with tf.Session() as session: #        #      x tf.global_variables_initializer().run() #     f   #   feed_dict    placeholder' #    b = -5 #      ,    result_f, result_a, result_x, result_b = session.run([f, a, x, b], feed_dict={b: -5}) print("f = %.1f * %.1f + %.1f = %.1f" % (result_a, result_x, result_b, result_f)) print("a = %.1f" % a.eval()) #   ,    #  eval    run  ,       ( feed_dict) #      ,   : x = x.assign_add(1.0) print("x = %.1f" % x.eval()) # : # f = 2.0 * 3.0 + -5.0 = 1.0 # a = 2.0 # x = 4.0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そのため、プレースホルダーは新しいデータがモデルに転送されるノードであり、変数（変数）はグラフの実行中に変更できるノードです。 上記の資料がすべての人に明確であることを願っています。なぜなら、 最初のモデルの学習を開始するだけで十分です。 前のコードフラグメントでは、線形関数のグラフをコンパイルしました $$ $インライン$ a \ cdot x + b $インライン$ さあ、もう少し進んで関数を近似してみましょう $$ $インライン$ a \ cdot x + b $インライン$ ポイントのセットによって。 はい、私はこのタスクがシンボルといくつかの決まり文句のある例の認識だけでなく、すでにすべての人を悩ませていることを知っていますが、調和して、あなたはそれらのすべてを通過しなければなりません...

最初の学習アルゴリズム

テンソルフローでモデルをトレーニングするには、損失関数と最適化アルゴリズム自体の2つを追加する必要があります。



損失関数は、モデルによって予測された関数の値と実際の値を取り、それらの間の距離を返す関数です（この値をエラーと呼びます）。 たとえば、実際の値を予測する場合、損失関数として、引数の差の2乗または差のモジュラスを取ることができます。 分類に問題がある場合、損失関数は正解に対して0を返し、エラーに対して1を返します。 大まかに言えば、損失関数は負ではない実数を返す必要があり、それが大きいほど、モデルが強くなるほど、モデルをトレーニングするタスクは最小化されます。 最後の文は完全に正しいわけではありませんが、機械学習の考え方を完全に反映しています。



最適化方法のうち、古典的な勾配降下のみを考慮します。 彼についてはすでに多くのことが書かれているので、「レンガごとに」分解して詳細を説明することはしません（とにかく素材は小さくありません）。 ただし、理解する必要があるため、視覚化を使用して方法を簡潔かつ明確に説明しようとします。 以下は同じチャートの2つのオプションです- $$ $ inline $ \ sin \ left（\ frac12x ^ 2- \ frac14y ^ 2 \ right）+ \ cos（2x + 1）$ inline $ 。 このメソッドのタスクは、極小値を見つけることです。 点から（グラフ上でランダムに取得 $$ $インライン$ \左（\ frac12; \ frac12 \右）$インライン$ ）くぼみに入ります（グラフの青い領域）。





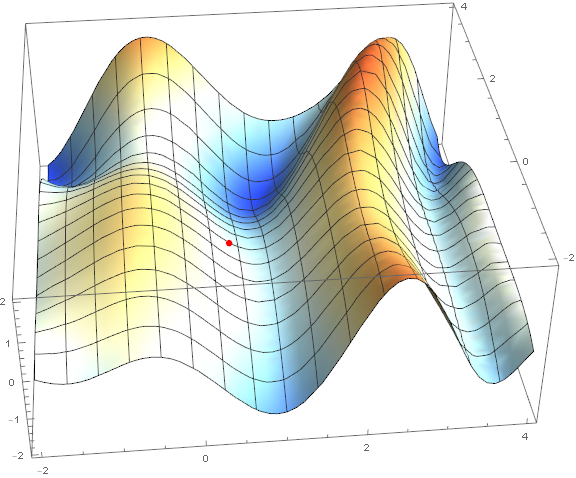
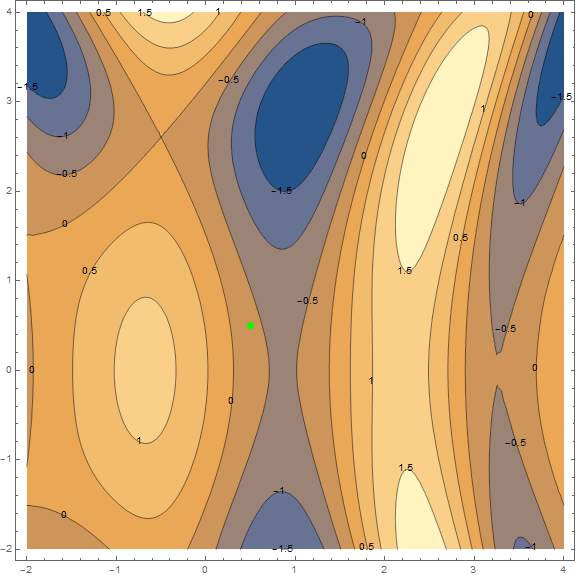
この方法の本質は、現在の点で関数の勾配とは反対の方向に進むことです。 勾配は、関数の最大の成長の方向を指すベクトルです。 数学的には、これはすべての引数に関する導関数のベクトルです- $$ $ inline $ \ mathrm {grad}（f）= \ nabla f = \ left（\ frac {\ partial f} {\ partial x}、\; \ frac {\ partial f} {\ partial y} \右）$インライン$ 。 関数はランダムに取得され、計算は行われません。実際には、アルゴリズムのいくつかのステップの視覚化を見て、より簡単な例があります。





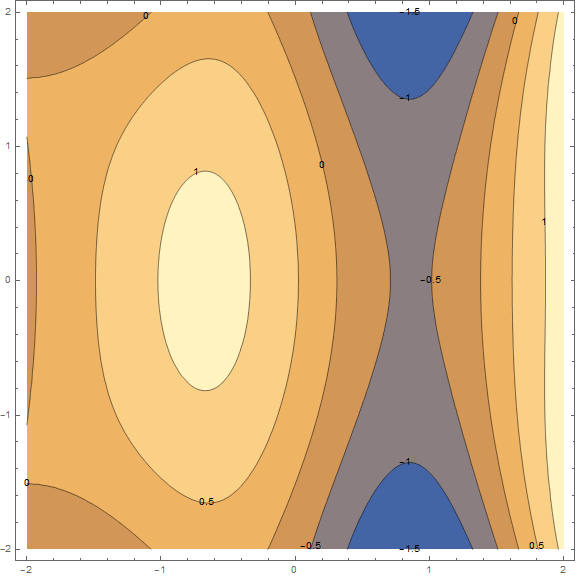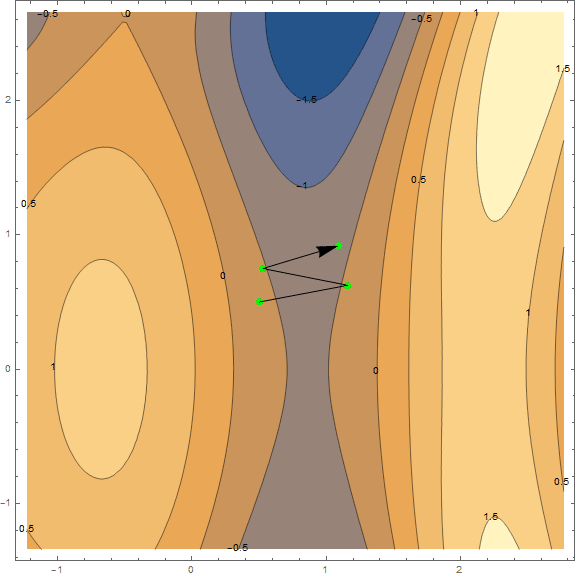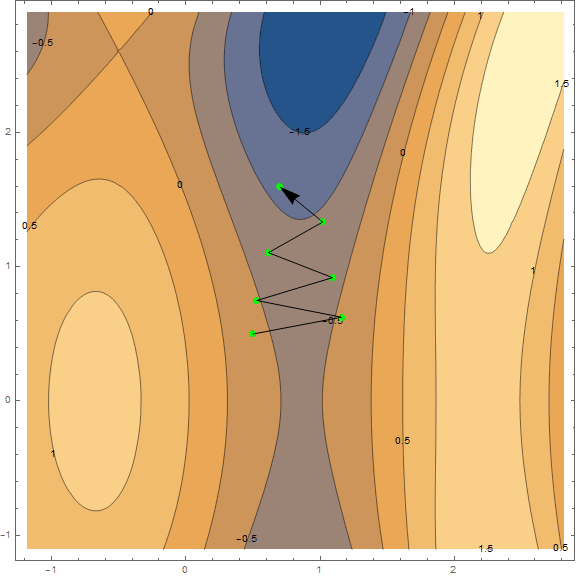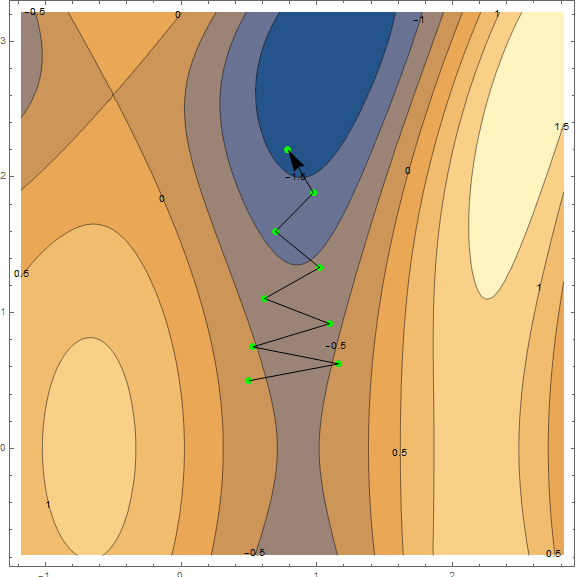
それとは別に、最小限に移動する必要がある速度に言及する価値があります（機械学習のタスクに関連して、これは学習速度と呼ばれます）。 最初の結果を得るには、固定速度を選択するだけで十分です。 ただし、多くの場合、アルゴリズムの実行中に値を小さくすることをお勧めします。 より小さなステップで移動します。 これで十分ですが、必要に応じて、実際の方法をより詳細に分析します。



次の例では、関数の値を復元しようとします $$ $インライン$ 2x-3 $インライン$ 正規分布ノイズの50ポイントで-2〜2の範囲。 確率的勾配降下法（SGD-確率的勾配降下法）を使用して、5点のセット（パッケージ）でモデルをトレーニングします。 コードをすぐに見てみましょう。

 import numpy as np import tensorflow as tf %matplotlib inline import matplotlib.pyplot as plt samples = 50 #   packetSize = 5 #   def f(x): return 2*x-3 #   x_0 = -2 #   x_l = 2 #   sigma = 0.5 #    np.random.seed(0) #    (          ) data_x = np.arange(x_0,x_l,(x_l-x_0)/samples) #  [-2, -1.92, -1.84, ..., 1.92, 2] np.random.shuffle(data_x) # ,    data_y = list(map(f, data_x)) + np.random.normal(0, sigma, samples) #      print(",".join(list(map(str,data_x[:packetSize])))) #    print(",".join(list(map(str,data_y[:packetSize])))) #     tf_data_x = tf.placeholder(tf.float32, shape=(packetSize,)) #        tf_data_y = tf.placeholder(tf.float32, shape=(packetSize,)) #        weight = tf.Variable(initial_value=0.1, dtype=tf.float32, name="a") bias = tf.Variable(initial_value=0.0, dtype=tf.float32, name="b") model = tf.add(tf.multiply(tf_data_x, weight), bias) loss = tf.reduce_mean(tf.square(model-tf_data_y)) #  ,    optimizer = tf.train.GradientDescentOptimizer(0.5).minimize(loss) #  ,     with tf.Session() as session: tf.global_variables_initializer().run() for i in range(samples//packetSize): feed_dict={tf_data_x: data_x[i*packetSize:(i+1)*packetSize], tf_data_y: data_y[i*packetSize:(i+1)*packetSize]} _, l = session.run([optimizer, loss], feed_dict=feed_dict) #     "" print(": %f" % (l, )) print("a = %f, b = %f" % (weight.eval(), bias.eval())) plt.plot(data_x, list(map(lambda x: weight.eval()*x+bias.eval(), data_x)), data_x, data_y, 'ro')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

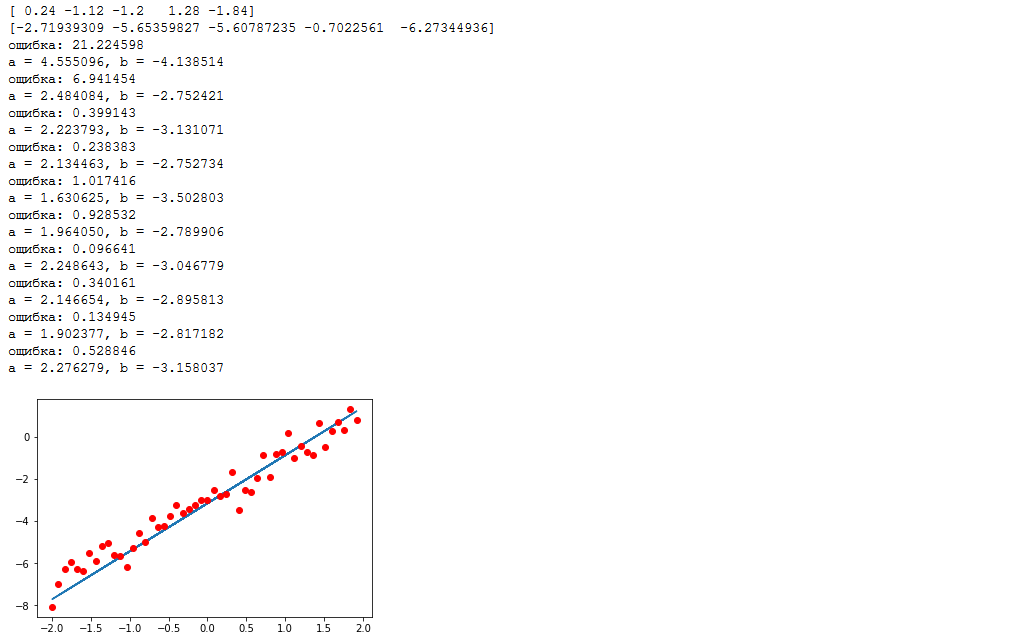
グラフは次のようになります。



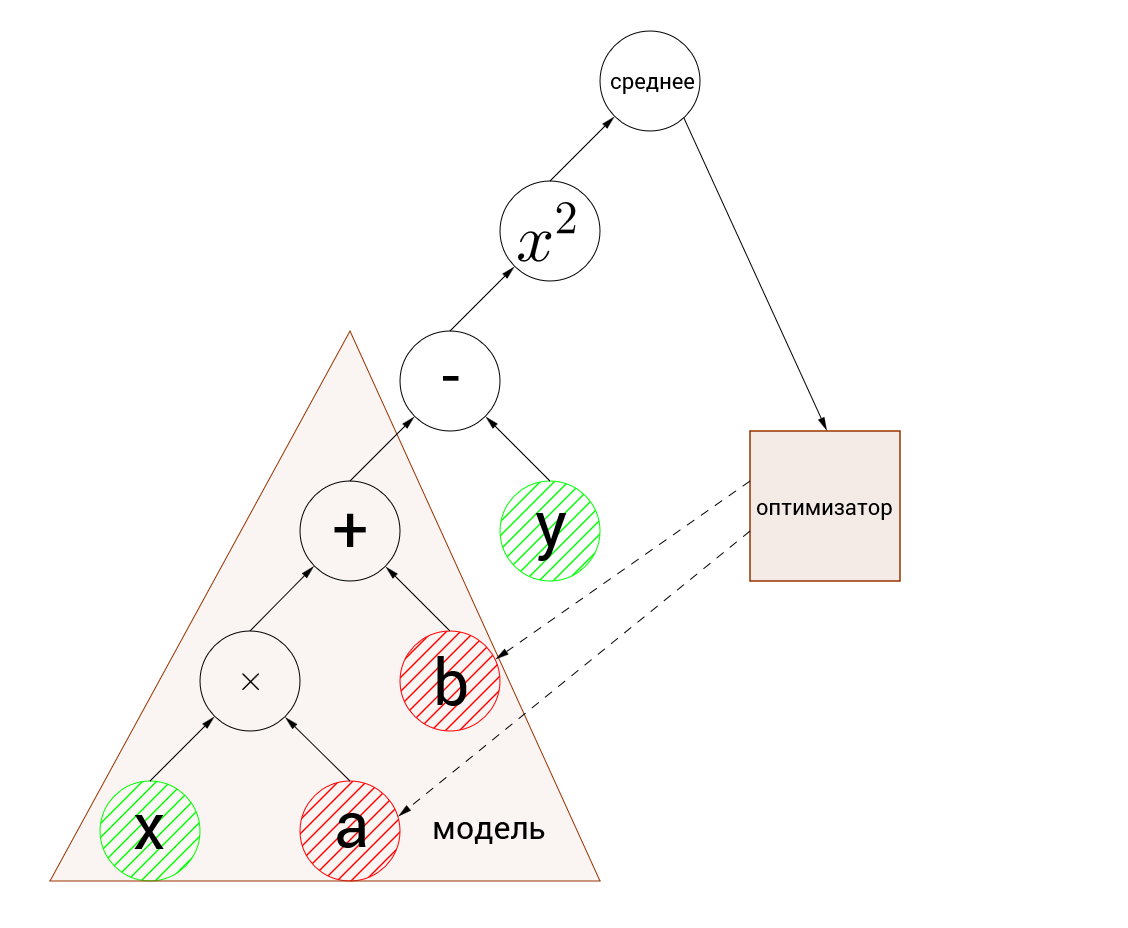
入力ノードは緑色で強調表示され、最適化された変数は赤色で強調表示されます。



最初に目を引くのは、入力ノードの次元と変数の不一致です。 入力ノードは5つの要素の配列を受け入れ、変数は数値です。 これをブロードキャストと呼びます。 大まかに言うと、1つに余分な次元がある配列で計算を実行する必要がある場合、計算はより大きな配列の各要素に対して個別に実行され、結果はより大きな次元の配列になります。 つまり [1,2,3,4,5] + 1 = [2,3,4,5,6]、定式化するのはかなり困難ですが、直感的に理解できるはずです。



アルゴリズムのアクションを手動で詳しく説明しましょう。これが何が起こっているのかを理解する最良の方法だと思います。 そのため、引数-[0.24、-1.12、-1.2、1.28、-1.84]および値[-2.72、-5.65、-5.61、-0.70、-6.27]（100分の1に丸められます）が入力に渡されます。 まず、関数の値をバッチ計算します。変数が初期化された後、関数は次のようになります。 $$ $インライン$ 0.1 \ cdot x + 0 $インライン$ 。 各引数を代入します：

$$ $$表示$$ \左[\ begin {matrix} 0.1 \ cdot 0.24 + 0 = 0.024 \\ 0.1 \ cdot -1.12 + 0 = -0.112 \\ 0.1 \ cdot -1.2 + 0 = -0.12 \\ 0.1 \ cdot 1.28 + 0 = 0.128 \\ 0.1 \ cdot -1.84 + 0 = -0.184 \ end {matrix} \ right。$$表示$$

さらに、得られた値は基準値から減算され、二乗され、平均値が計算されます。

$$ $$表示$$ \左[\ begin {matrix}（0.024-（-2.72））^ 2 \約7.53 \\（-0.112-（-5.65））^ 2 \約30.67 \\（-0.12- （-5.61））^ 2 \約30.14 \\（0.128-0.7）^ 2 \約0.69 \\（-0.184-（-6.27））^ 2 \約37.04 \ end {matrix} \ right。\右矢印\ frac {7.53 + 30.67 + 30.14 + 0.69 + 37.04} 5 \約21.21 $$表示$$

ログに表示される値と約100分の1の差は、計算中に100分の1に四捨五入することによって発生します。 したがって、エラーを計算しました。最適化に対処する時が来ました。 上のグラフの画像では、点線の矢印はオプティマイザーが変数を変更することを示しています。 勾配降下がどのように機能するかについて、すでに直感的に理解している必要があります。 この例では、速度0.5で確率的勾配降下を使用しています。 順番に見てみましょう。変数aとbを最適化して、それらから勾配を見つけます。

$$ $$ display $$ f =（a \ cdot x + b-y）^ 2 \ Rightarrow \ left \ {\ begin {matrix} \ frac {\ partial f} {\ partial a} = 2x（ax + by）\ \\ frac {\ partial f} {\ partial b} = 2（ax + by）\ end {matrix} \ right。$$ display $$

ポイントのセット全体にわたって値を改善する必要があるため、便宜上、変数ごとに勾配の平均値を個別に計算します。

$$ $$表示$$ \ begin {matrix} a \ Rightarrow \ frac {1.31712 +（-12.4051）+（-13.176）+2.11968 +（-22.3965）} {5} =-8.90816 \\ b \ Rightarrow \ frac {5.488 + 11.076 + 10.98 + 1.656 + 12.172} {5} = 8.2744 \ end {matrix} $$ディスプレイ$$

そして最後に、与えられた速度を考慮して最適化された変数の値を変更します。

$$ $$ display $$ \ begin {matrix} a_ {new} = a_ {old} -0.5 \ cdot-8.90816 = 0.1-0.5 \ cdot（-8.90816）= 4.55 \\ b_ {new} = b_ {old} -0.5 \ cdot8.2744 = 0-0.5 \ cdot（-8.90816）=-4.14 \ end {matrix} $$ display $$

値 $$ $インライン$ a_ {new} $インライン$ そして $$ $インライン$ b_ {new} $インライン$ そして、変数の望ましい値があります。 これらの計算は、ポイントの各セットでサイクルで繰り返されます。 この方法が確率論と呼ばれるのはなぜですか？ なぜなら、一度にすべてのポイントではなく、小さなデータ（パケット）でのみ勾配を計算するからです。 したがって、確率的降下では必要な計算ははるかに少なくなりますが、各反復でのエラーの削減は保証されません。 奇妙なことに、この時間的な収束の大きさの「ノイズ」は有用な場合さえあります。 ローカルミニマムから「抜け出す」ことができます。



実際、これはまだ終了する可能性があります。 記事は比較的小さいことが判明しましたが、これは喜ばしいことです。 この種の資料を書いているのはこれが初めてなので、いくつかの点が詳細または間違った方法でカバーされていないと思う場合は、それについて書いてください-記事は建設的な批判に基づいて確実に補足され、調整されます。 さらに、以下のパートの公開準備を改善するのに役立ちます。これらのパートは、ここで必ず投稿されます（もちろん、記事が否定的に満たされるシナリオを除きます）。



結論として、私は友人のニコライ・サガネンコが資料の準備に協力してくれたことに感謝したいと思います。 個人的な使用のための私の小さなベビーベッドが上記の意識の流れに変わったのは彼のおかげでした。