🧒🏿 🧘🏽 🍤 電気回路シミュレーション 🌰 👬 💪🏽

この出版物では、状態変数を使用して電気回路をモデル化する方法について説明しています。

この出版物は、この方法による電気回路のモデリングに関する少なくとも1つのhow2がロシア語であることを確認するためのものです。かつて、私は多くのグーグルを検索しましたが、通常の素材に出会ったことはありません。すべてのマニュアルとテキストには理論のみが含まれていました。さらに、私が見つけた材料には、完全な解決サイクルがありませんでした。

スキーム⟶方程式⟶数値解法⟶グラフィックス。

実際、これはアクションのアルゴリズムです。

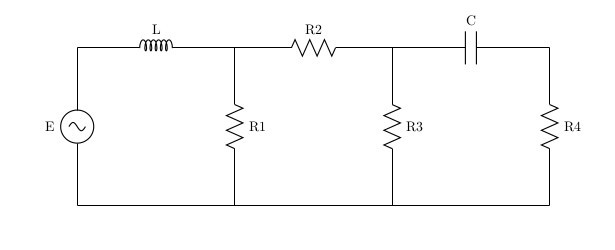
スキームがあり、今はオームとキルヒホフの法則を使用して方程式を作成する必要があります。

成分方程式：

C * f r a c d U_{c} d t = i_{c}; L * f r a c d i_{l} d t = U_{L};

$C * \ frac {d {U_ {c}}} {d {t}} = i_ {c}; L * \ frac {d {i_ {l}}} {d {t}} = U_ {L};$

U_{1} = i_{1} * R_{1}; U_{2} = i_{2} * R_{2}; U_{3} = i_{3} * R_{3}; U_{4} = i_{4} * R_{4}; U_{1} = i_{1} * R_{1};

$U_ {1} = i_ {1} * R_ {1}; U_ {2} = i_ {2} * R_ {2}; U_ {3} = i_ {3} * R_ {3}; U_ {4} = i_ {4} * R_ {4}; U_ {1} = i_ {1} * R_ {1};$

輪郭方程式：

E - U_{L} - U_{1} = 0;

$E-U_ {L} -U_ {1} = 0;$

U_{1} - U_{2} - U_{3} = 0;

$U_ {1} -U_ {2} -U_ {3} = 0;$

U_{3} - U_{C} - U_{4} = 0;

$U_ {3} -U_ {C} -U_ {4} = 0;$

節点方程式：

i_{L} - i_{1} - i_{2} = 0;

$i_ {L}-i_ {1}-i_ {2} = 0;$

i_{2} - i_{3} - i_{4} = 0;

$i_ {2}-i_ {3}-i_ {4} = 0;$

i_{c} = i_{4};

$i_ {c} = i_ {4};$

次に、微分方程式を導出する必要があります。この方法では、状態変数のためにコンデンサーとインダクターの磁束結合を充電するのが一般的です。これらの値がわかれば、ノードとブランチの電圧と電流を引き出すことができます。また：

方程式は独立している必要があります。
方程式には、状態変数とソースのみを含める必要があります。他のすべての変数は、状態変数で表現する必要があります。
状態変数の一次導関数は、各方程式の左側に入力する必要があります。右側に派生物がないはずです。

最初の微分方程式を導きます：

U_{L} = E - U_{1} = E - U_{2} - U_{3} = E - U_{2} - U_{C} - U_{4};

$U_ {L} = E-U_ {1} = E-U_ {2} -U_ {3} = E-U_ {2} -U_ {C} -U_ {4};$

U_{L} = E - i_{2} * R_{2} - U_{C} - i_{C} * R_{4} = E - （ i_{L} - f r a c E - U_{L} R_{1} ） * R_{2} - U_{C} - i_{C} * R_{4};

$U_ {L} = E-i_ {2} * R_ {2} -U_ {C} -i_ {C} * R_ {4} = E-（i_ {L}-\ frac {E-U_ {L} } {R_ {1}}）* R_ {2} -U_ {C} -i_ {C} * R_ {4};$

U_{L} = E - i_{L} * R_{2} + E * f r a c R_{2} R_{1} - U_{L} * f r a c R_{2} R_{1} - U_{C} - i_{C} * R_{4};

$U_ {L} = E-i_ {L} * R_ {2} + E * \ frac {R_ {2}} {R_ {1}}-U_ {L} * \ frac {R_ {2}} {R_ {1}}-U_ {C} -i_ {C} * R_ {4};$

U_{L} * f r a c R_{1} + R_{2} R_{1} = E * f r a c R_{1} + R_{2} R_{1} - i_{L} * R_{2} - U_{C} - i_{C} * R_{4};

$U_ {L} * \ frac {R_ {1} + R_ {2}} {R_ {1}} = E * \ frac {R_ {1} + R_ {2}} {R_ {1}}-i_ { L} * R_ {2} -U_ {C} -i_ {C} * R_ {4};$

i_{C} = i_{L} - i_{1} - i_{3} = i_{L} - f r a c E - U_{L} R_{1} - f r a c U_{C} + i_{C} * R_{4} R_{3};

$i_ {C} = i_ {L} -i_ {1} -i_ {3} = i_ {L}-\ frac {E-U_ {L}} {R_ {1}}-\ frac {U_ {C} + i_ {C} * R_ {4}} {R_ {3}};$

i_{C} f r a c R_{3} + R_{4} R_{3} = i_{L} - f r a c E - U_{L} R_{1} - f r a c U_{C} R_{3};

$i_ {C} \ frac {R_ {3} + R_ {4}} {R_ {3}} = i_ {L}-\ frac {E-U_ {L}} {R_ {1}}-\ frac { U_ {C}} {R_ {3}};$

コイルの電圧の式でコンデンサ電流を代入します。

U_{L} * f r a c R_{1} + R_{2} R_{1} = E * f r a c R_{1} + R_{2} R_{1} - i_{L} * R_{2} - U_{C} - f r a c R_{3} * R_{4} R_{3} + R 4 * （ i_{L} - f r a c E R_{1} + f r a c U_{L} R_{1} - f r a c U_{C} R_{3} ）;

$U_ {L} * \ frac {R_ {1} + R_ {2}} {R_ {1}} = E * \ frac {R_ {1} + R_ {2}} {R_ {1}}-i_ { L} * R_ {2} -U_ {C}-\ frac {R_ {3} * R_ {4}} {R_ {3} + R {4}} *（i_ {L}-\ frac {E} { R_ {1}} + \ frac {U_ {L}} {R_ {1}}-\ frac {U_ {C}} {R_ {3}}）;$

方程式を変換すると、最初の微分方程式が得られます。

L * f r a c d i_{L} d t = U_{L} = E - f r a c R_{1} （ R_{1} + R_{2} ） * （ R_{3} + R_{4} ） + R_{3} * R_{4} * （ i_{L} * （ R_{2} * （ R_{3} + R_{4} ） + R_{3} ） - U_{C} * R_{3} ）;

$L * \ frac {di_ {L}} {dt} = U_ {L} = E- \ frac {R_ {1}} {（R_ {1} + R_ {2}）*（R_ {3} + R_ {4}）+ R_ {3} * R_ {4}} *（i_ {L} *（R_ {2} *（R_ {3} + R_ {4}）+ R_ {3}）-U_ {C} * R_ {3}）;$

二次微分方程式を導きます：

i_{C} = i_{L} - i_{1} - i_{3} = i_{L} - f r a c E - U_{L} R_{1} - f r a c U_{C} R_{3} - f r a c i_{C} * R_{4} R_{3};

$i_ {C} = i_ {L} -i_ {1} -i_ {3} = i_ {L}-\ frac {E-U_ {L}} {R_ {1}}-\ frac {U_ {C} } {R_ {3}}-\ frac {i_ {C} * R_ {4}} {R_ {3}};$

C * f r a c d U_{c} d t = i_{c} = f r a c R_{3} C * （ R_{3} + R_{4} ） * （ i_{L} - f r a c E - U_{L} R_{1} - f r a c U_{C} R_{3} ）

$C * \ frac {d {U_ {c}}} {d {t}} = i_ {c} = \ frac {R_ {3}} {C *（R_ {3} + R_ {4}）} * （i_ {L}-\ frac {E-U_ {L}} {R_ {1}}-\ frac {U_ {C}} {R_ {3}}）$

これで、数値的に解くことができる微分方程式系ができました。

b e g i n c a s e s L * f r a c d i_{L} d t = E - f r a c R_{1} （ R_{1} + R_{2} ） * （ R_{3} + R_{4} ） + R_{3} * R_{4} * （ i_{L} * （ R_{2} * （ R_{3} + R_{4} ） + R_{3} ） - U_{C} * R_{3} ）; C * f r a c d U_{c} d t = f r a c R_{3} C * （ R_{3} + R_{4} ） * （ i_{L} - f r a c E - U_{L} R_{1} - f r a c U_{C} R_{3} ）; e n d c a s e s

$\ begin {cases} L * \ frac {di_ {L}} {dt} = E- \ frac {R_ {1}} {（R_ {1} + R_ {2}）*（R_ {3} + R_ {4}）+ R_ {3} * R_ {4}} *（i_ {L} *（R_ {2} *（R_ {3} + R_ {4}）+ R_ {3}）-U_ {C} * R_ {3}）; \\ C * \ frac {d {U_ {c}}} {d {t}} = \ frac {R_ {3}} {C *（R_ {3} + R_ {4}）} *（i_ {L }-\ frac {E-U_ {L}} {R_ {1}}-\ frac {U_ {C}} {R_ {3}}）; \ end {cases}$

オイラー法を使用します ~~これは最も単純で~~ 、Pythonを使用しています。

X_{i} = X_{i - 1} + h * f r a c d X_{i - 1} d t

$X_ {i} = X_ {i-1} + h * \ frac {d {X_ {i-1}}} {d {t}}$

プログラム

import numpy as np import matplotlib.pyplot as plt #Input voltage amplitude AMP = 21.0 #Active components r1 = 2000.0; r2 = 10.0; r3 = 10.0; r4 =2000.0; #Reactive components c=0.0001; l=0.06; #Time components T=0.01; t0=0.0; step=T/1000; tf=T*10 steps=int(tf/step); #Input voltage def E(t): n=int(t/T) if ((t >= n*T )and(t <= n*T + T/2)): return AMP else: return 0.0 time = np.arange(t0, tf, step) ul = []; il = []; uc = []; ic = []; y = []; for i in range(0, steps, 1): y.append(E(time[i])) def dIl_dt(t): return float((1.0/l)*(E(t) - (r1/((r1+r2)*(r3+r4)+r3*r4) * (il[int(t/step)]*(r2*(r3+r4)+r3) - uc[int(t/step)]*r3)))) def dUc_dt(t): return float((1.0/c)* (r3/(r3+r4)) * (il[int(t/step)]-(E(t)-ul[int(t/step)])/r1 - uc[int(t/step)]/r3)) #Start condition ul.append(E(0)); il.append(0.0); uc.append(0.0); ic.append(0.0); #Euler method for i in range(1, steps, 1): il.append(il[i-1] + step*dIl_dt(time[i-1])) uc.append(uc[i-1] + step*dUc_dt(time[i-1])) ul.append(l*dIl_dt(time[i])) ic.append(c*dUc_dt(time[i])) plt.figure("charts") e = plt.subplot(311) e.plot(time, y) e.set_xlabel('time (s)') e.set_ylabel('E(t), (V)', color='b') plt.grid(True) UL = plt.subplot(312) UL.plot(time, ul) UL.set_xlabel('time (s)') UL.set_ylabel('Ul(t), (V)', color = 'b') IL = UL.twinx() IL.plot(time, il, 'r') IL.set_ylabel('Il(t), (A)', color = 'r') plt.grid(True) UC = plt.subplot(313) UC.plot(time, uc) UC.set_xlabel('time (s)') UC.set_ylabel('Uc(t), (V)', color = 'b') IC = UC.twinx() IC.plot(time, ic, color = 'r') IC.set_ylabel('Ic(t), (A)', color = 'r') plt.grid(True) plt.show()

シミュレーション結果：

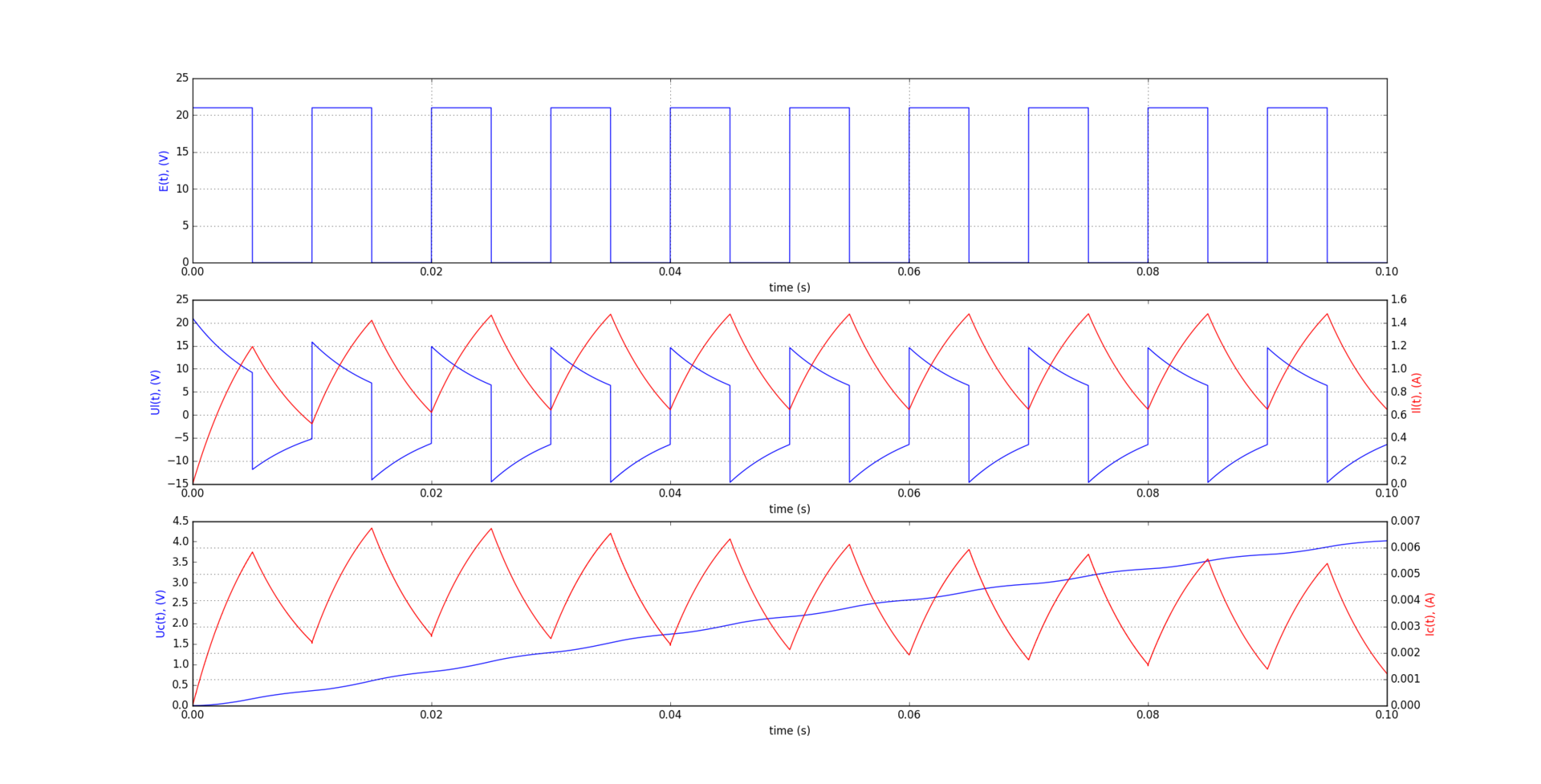
実際の計算のために他の方法を使用して差異を解決し、自己学習用の要素の電圧と電流のグラフを取得する方が、最も単純なオイラー法で十分です。電子工学では、最も一般的なニュートンラプソン法-ほとんどのCADシステムでは、この方法が使用されます。

文学から私はMathanov P.N.の本に助言しますおよびZeveke G.V.

また、あらゆる種類の技術（MSTU、サンクトペテルブルク、トムスクなど）および類似の資料のマニュアルは、そこに書かれている内容を理解するよりも簡単に捨てられます。ここで、キャッチフレーズは非常に不適切です。「単純化は難しく、複雑化は簡単です。」

電気回路シミュレーション

More articles: