パート2-DBSCAN
パート3-時系列クラスタリング
パート4-自己組織化マップ(SOM)
パート5-成長中の神経ガス(GNG)
少し手入れの行き届いたデータサイエンスの世界をもう少し詳しく見てみましょう。 現在、DBSCANクラスタリングアルゴリズムは準備中です。 任意の形状の塊が見つかったデータのクラスタリングに遭遇した、または遭遇しようとしている人々の削減をお願いします-今日、あなたの武器は優れたツールで補充されます。
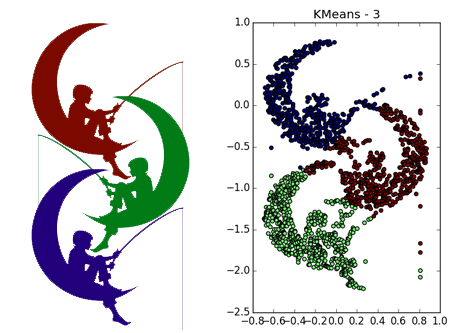
DBSCAN(ノイズを伴うアプリケーションの密度ベースの空間クラスタリング、ノイズが存在する密度空間クラスタリングアルゴリズム)は、その名前が示すように、データ密度で動作します。 入り口で、彼はすでにおなじみの近接行列と2つの神秘的なパラメータ-半径を求めます -近所と隣人の数。 そのため、すぐにそれらを選択する方法を理解することはできません。ここに密度と、DBSCANがノイズの多いデータをうまく処理する理由があります。 これがなければ、その適用性の限界を判断することは困難です。
それを理解しましょう。 前回の記事のように、最初にアルゴリズムの投機的な説明に目を向け、次にそのアルゴリズムを要約することを提案します。 私はQuoraにつまずいたという説明が好きなので、車輪を再発明することはせず、いくつかの小さな修正を加えてここで再現します。
直感的な説明
巨大なホールでは、大勢の人が誰かの誕生日を祝います。 一人でうろついている人がいますが、ほとんどは仲間です。 一部の企業は単に群衆の中に群がり、一部の企業は踊ったり、ランバダを踊ったりします。
部屋の人々をグループに分けたいです。
しかし、そのようなさまざまな形のグループを区別する方法、そして独身者を忘れないようにする方法さえありますか? 各人の周りの群衆密度を評価してみましょう。 おそらく、2人の間の群衆密度が特定のしきい値を超えている場合、それらは1つの会社に属します。 実際、「電車」を運転する人々が異なるグループに属している場合、たとえそれらの間のチェーンの密度が特定の制限内で変動する場合でも、奇妙になります。
他の数人が彼の近くに立っている場合、群衆が誰かの近くに集まったと言います。 ええ、2つのパラメーターを設定する必要があることがすぐにわかります。 近いとはどういう意味ですか? 直感的な距離を取ります。 人々がお互いの頭に触れることができるなら、彼らは近くにいると言います。 メーターについて。 さて、「他の数人」は何人いますか? 3人としましょう。 二人はそのように散歩に行くことができますが、三番目は間違いなく余分です。
誰もが彼から1メートルの半径内に立つ人の数を計算します。 少なくとも3人の隣人がいる全員が緑の旗を掲げます。 今、それらはルート要素であり、グループを形成するのは彼らです。
隣人が3人未満の人に頼ります。 少なくとも1人の隣人が緑の旗を持っている人を選択し、黄色の旗を渡します。 彼らがグループの境界にいるとしましょう。
3人の隣人がいないだけでなく、緑色の旗を持っている人もいませんでした。 それらに赤い旗を与えましょう。 それらはどのグループにも属さないと仮定します。
したがって、ある人から別の人に「グリーン」な人のチェーンを作成できる場合、これらの2人は同じグループに属します。 明らかに、そのようなクラスターはすべて、空のスペースまたは黄色の旗を持つ人々によって分離されています。 番号を付けることができます。グループNo. 1の全員がグループNo. 1のお互いの手のチェーンに到達できますが、No。2、No。3などには誰もアクセスできません。 他のグループについても同じです。
黄色のフラグを持つ人の隣に「緑」の隣人が1人しかいない場合、その人は自分の隣人が属するグループに属します。 そのような近隣が複数あり、それらに異なるグループがある場合は、選択する必要があります。 ここでは、さまざまな方法を使用できます。たとえば、どの隣人が最も近いかを確認します。 何とかしてエッジケースを回避する必要がありますが、それでかまいません。
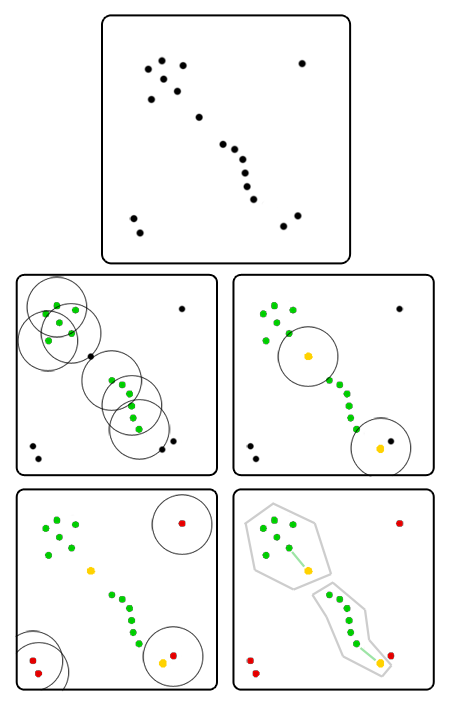
原則として、群衆のすべての土着の要素を一度にマークすることは意味がありません。 グループの各ルート要素からお互いにチェーンを描くことができるので、回り道を開始する方法は関係ありません。遅かれ早かれ誰もが見つかります。 ここでは、反復オプションの方が優れています。
- 群衆の中からランダムな人に近づきます。
- 彼の隣に3人未満の人がいる場合、彼を可能な隠者のリストに移し、他の誰かを選びます。
- そうでなければ:
- 回避する必要がある人々のリストから彼を除外します。
- この人に緑の旗を渡し、彼がこれまで唯一の住民である新しいグループを作成します。
- 私たちは彼のすべての隣人を回ります 彼の隣人がすでに潜在的なシングルのリストに載っている場合、または彼の隣に他の人がほとんどいない場合、群衆の端にいます。 簡単にするために、すぐに黄色のフラグでフラグを立て、グループに添付してツアーを続行できます。 隣人も「緑」であることが判明した場合、隣人は新しいグループを開始せず、すでに作成されているグループに参加します。 さらに、ネイバーをバイパスのネイバーリストに追加します。 クロールリストが空になるまで、この手順を繰り返します。
- 何らかの方法ですべての人を回避するまで、手順1〜3を繰り返します。
- 隠者のリストを扱います。 ステップ3で地域のすべてをすでに分散している場合、単一の排出のみがそこに残っていました。すぐに終了できます。 そうでない場合は、リストに残っている人々を何らかの方法で配布する必要があります。
正式なアプローチ
いくつかの定義を紹介します。 いくつかの対称距離関数を与えてみましょう および定数 そして 。 それから
- 地域に名前を付ける そのために 、 -オブジェクトの近傍 。
- ルートオブジェクトまたは核オブジェクト度 オブジェクトと呼ばれる その近隣には少なくとも オブジェクト: 。
- 対象 オブジェクトから直接密に到達可能 もし
そして ルートオブジェクトです。
- 対象 オブジェクトからしっかりと到達可能 もし そのような から直接密に到達可能
ルートオブジェクトを選択する データセットから、それをマークし、その直接密に到達可能なすべてのネイバーをバイパスリストに入れます。 それぞれについて リストから:このポイントをマークし、ルートでもある場合は、すべての隣接ノードをバイパスリストに追加します。 このアルゴリズムの過程で形成されたラベル付きポイントのクラスターは最大である(つまり、条件を満たすために別のポイントで拡張できない)ことは簡単に証明され、厳密な到達可能性の意味で接続されています。 つまり、すべてのポイントをバイパスしていなければ、他のルートオブジェクトからクロールを再開でき、新しいクラスターは以前のものを吸収しません。
ちょっと待ってください...はい、これは制限付きのグラフの幅のマスクされたバイパスです! そのため、バイパス条件とエッジポイントを持つフリルのみが追加されています。
ウィキペディアは、擬似コードアルゴリズムのフレームワークを親切に提供します
擬似コード
DBSCAN(D, eps, MinPts) { C = 0 for each point P in dataset D { if P is visited continue next point mark P as visited NeighborPts = regionQuery(P, eps) if sizeof(NeighborPts) < MinPts mark P as NOISE else { C = next cluster expandCluster(P, NeighborPts, C, eps, MinPts) } } } expandCluster(P, NeighborPts, C, eps, MinPts) { add P to cluster C for each point Q in NeighborPts { if Q is not visited { mark Q as visited QNeighborPts = regionQuery(Q, eps) if sizeof(QNeighborPts) >= MinPts NeighborPts = NeighborPts joined with QNeighborPts } if Q is not yet member of any cluster add Q to cluster C } } regionQuery(P, eps) return all points within P eps-neighborhood (including P)
または、非常に単純なpython実装である擬似コードを好まない人向け
Python
from itertools import cycle from math import hypot from numpy import random import matplotlib.pyplot as plt def dbscan_naive(P, eps, m, distance): NOISE = 0 C = 0 visited_points = set() clustered_points = set() clusters = {NOISE: []} def region_query(p): return [q for q in P if distance(p, q) < eps] def expand_cluster(p, neighbours): if C not in clusters: clusters[C] = [] clusters[C].append(p) clustered_points.add(p) while neighbours: q = neighbours.pop() if q not in visited_points: visited_points.add(q) neighbourz = region_query(q) if len(neighbourz) > m: neighbours.extend(neighbourz) if q not in clustered_points: clustered_points.add(q) clusters[C].append(q) if q in clusters[NOISE]: clusters[NOISE].remove(q) for p in P: if p in visited_points: continue visited_points.add(p) neighbours = region_query(p) if len(neighbours) < m: clusters[NOISE].append(p) else: C += 1 expand_cluster(p, neighbours) return clusters if __name__ == "__main__": P = [(random.randn()/6, random.randn()/6) for i in range(150)] P.extend([(random.randn()/4 + 2.5, random.randn()/5) for i in range(150)]) P.extend([(random.randn()/5 + 1, random.randn()/2 + 1) for i in range(150)]) P.extend([(i/25 - 1, + random.randn()/20 - 1) for i in range(100)]) P.extend([(i/25 - 2.5, 3 - (i/50 - 2)**2 + random.randn()/20) for i in range(150)]) clusters = dbscan_naive(P, 0.2, 4, lambda x, y: hypot(x[0] - y[0], x[1] - y[1])) for c, points in zip(cycle('bgrcmykgrcmykgrcmykgrcmykgrcmykgrcmyk'), clusters.values()): X = [p[0] for p in points] Y = [p[1] for p in points] plt.scatter(X, Y, c=c) plt.show()
PythonでのDBSCANのより適切な実装の例は、 sklearnパッケージにあります。 Matlabでの実装例はすでにHabréにありました 。 Rを好む場合は、 こちらとこちらをご覧ください 。
アプリケーションのニュアンス
理想的には、DBSCANは複雑さを達成できます しかし、あなたは本当にそれに頼るべきではありません。 毎回カウントしない場合 ポイント、その後、予想される難易度は 。 最悪の場合(不良データまたはブルートフォース実装)- 。 素朴なDBSCAN実装は食い物にしたい 距離行列のメモリ-これは明らかに冗長です。 アルゴリズムの多くのバージョンは、より緩やかなデータ構造で機能します。sklearnとRの実装は、すぐにKDツリーを使用して最適化できます。 残念ながら、バグがあるため、これは常に機能するとは限りません。
エッジポイントを処理するための非ランダムルールを使用したDBSCANは決定論的です。 ただし、作業を高速化し、パラメーターの数を減らすために、ほとんどの実装では、それらに到達する最初のクラスターにエッジポイントを与えます。 たとえば、異なる起動の上の画像の中央の黄色い点は、下側クラスターと上側クラスターの両方に属することができます。 原則として、これはアルゴリズムの品質に大きな影響を与えません。これは、クラスターがまだ境界点を通過しないためです-ポイントがクラスターからクラスターにジャンプして他のポイントに「道を開く」状況は不可能です
DBSCANはクラスターの中心を独立して計算しませんが、特にクラスターの任意の形状を考慮すると、これはほとんど問題になりません。 ただし、DBSCANは自動的に放出を検出します。
比率 どこで -空間の次元は、空間の領域内のデータポイントのしきい値密度と直感的に見なすことができます。 同じ比率であることが期待される 、結果はほぼ同じになります。 時々これは真実ですが、アルゴリズムが1つではなく2つのパラメーターを設定する必要がある理由があります。 まず、異なるデータセット内のポイント間の一般的な距離は異なります-常に明示的に半径を設定する必要があります。 第二に、データセットの不均一性が役割を果たします。 以上 そして 、アルゴリズムがクラスター内の密度変動を「許容」する傾向が強い。 一方で、これは便利な場合があります。単に十分なデータがなかったクラスターに「穴」が見えるのは不快です。 一方、クラスター間に明確な境界がない場合、またはノイズがクラスター間に「ブリッジ」を作成する場合は有害です。 次に、DBSCANは2つの異なるグループを簡単に接続します。 これらのパラメータのバランスは、DBSCANを使用する複雑さです。実際のデータセットには、さまざまなぼかしの程度の境界を持つさまざまな密度のクラスタが含まれます。 クラスター間の境界の密度が分離されたクラスターの密度以上である条件下では、何かを犠牲にする必要があります。
この問題を軽減できるDBSCAN オプション があり ます 。 アイデアは調整することです アルゴリズムが機能するにつれて、さまざまな分野で。 残念ながら、アルゴリズムパラメータの数は増加しています。
選択できるヒューリスティックがあります。 そして 。 ほとんどの場合、この方法とそのバリエーションが使用されます。
- 選択してください 。 通常、3〜9の値が使用され、データセットの不均一性が予想されるほど、ノイズレベルが大きくなるほど、より多くの値を取得する必要があります。 。
- 平均距離を計算します 各ポイントの最近傍。 つまり もし 、3つの最近傍を選択し、距離を加算して3で割る必要があります。
- 取得した値を昇順に並べ替えて、画面に表示します。
- このような急激に増加するグラフのようなものが見られます。 取るべき 最も強い変曲が発生するストリップのどこか。 以上 、より多くのクラスターを取得し、それらはより少なくなります。
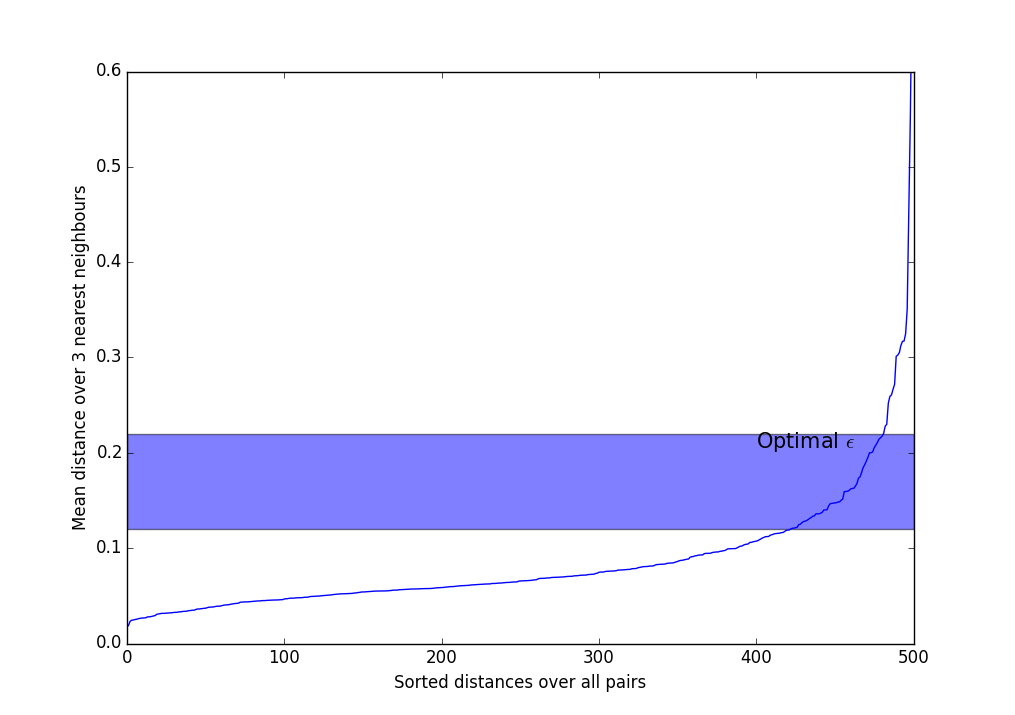
についてのより良い直観を得るために そして こちらからオンラインでオプションを試すことができます 。 DBSCANリングを選択し、スライダーをドラッグします。
いずれにせよ、DBSCANの主な欠点は、開口部を介してクラスターを接続できないことと、逆に、密集したジャンパーを介して明らかに異なるクラスターを接続できないことです。 これは、データディメンションが増加する理由の一部です。 後ろの陰湿な刺し傷は次元の呪いをかけます。 、開口部や橋が誤って発生する可能性のある場所が増えます。 十分な数のデータポイントがあることを思い出させてください 増加とともに指数関数的に増加 。
DBSCANは高度に変更可能です。 ここでは、加速のためにDBSCANとk-meansを交差させることを提案しています。 この記事は美しいグラフを示していますが、そのようなアルゴリズムが空間の次元よりはるかに小さい次元のクラスターにどのように作用するかは完全にはわかりません。 ガウス混合交差オプションとアルゴリズムのノンパラメトリックバージョンも参照してください。
DBSCANは並列化されていますが、これを効率的に行うのは簡単ではありません。 プロセス番号1がその数を見つけた場合 -サブクラスター、およびプロセス番号2 -サブクラスター、および それから そして 組み合わせることができます。 問題は、リストの絶え間ない同期がパフォーマンスを大きく損なうため、セットの共通部分が空ではないことに気付くことです。 実装オプションについては、 これらの 記事をご覧ください。
実験
開けないで、中の写真
同じデータをk-meansとAffinity伝播で分割するには、以前の投稿を参照してください。
DBSCANは、高密度で十分に分離されたクラスターで優れた機能を発揮します。 さらに、その形状はまったく重要ではありません。 おそらく、DBSCANは、小さなクラスターの検出において、すべての非専門アルゴリズムよりも優れています。



4行の例では、パラメーターに応じて、行のギャップにより8クラスターと4クラスターの両方を取得できることに注意してください。 一般的に、これは望ましい動作です-分布が正しいかどうか、または単に十分なデータがないかどうかは不明です。 ここでは幸運でした。線間の距離が開口部のサイズよりも大きいです。 また、スパイラルを使用した例では、どのポイントが異なるクラスターに属しているかに注意してください。 クラスターに割り当てられたスパイラルの長さは、近隣の数の減少とともに増加します。 スパイラルの中心に近いほど、ポイントは密になります。
さまざまなサイズの蓄積が適切に決定されます...
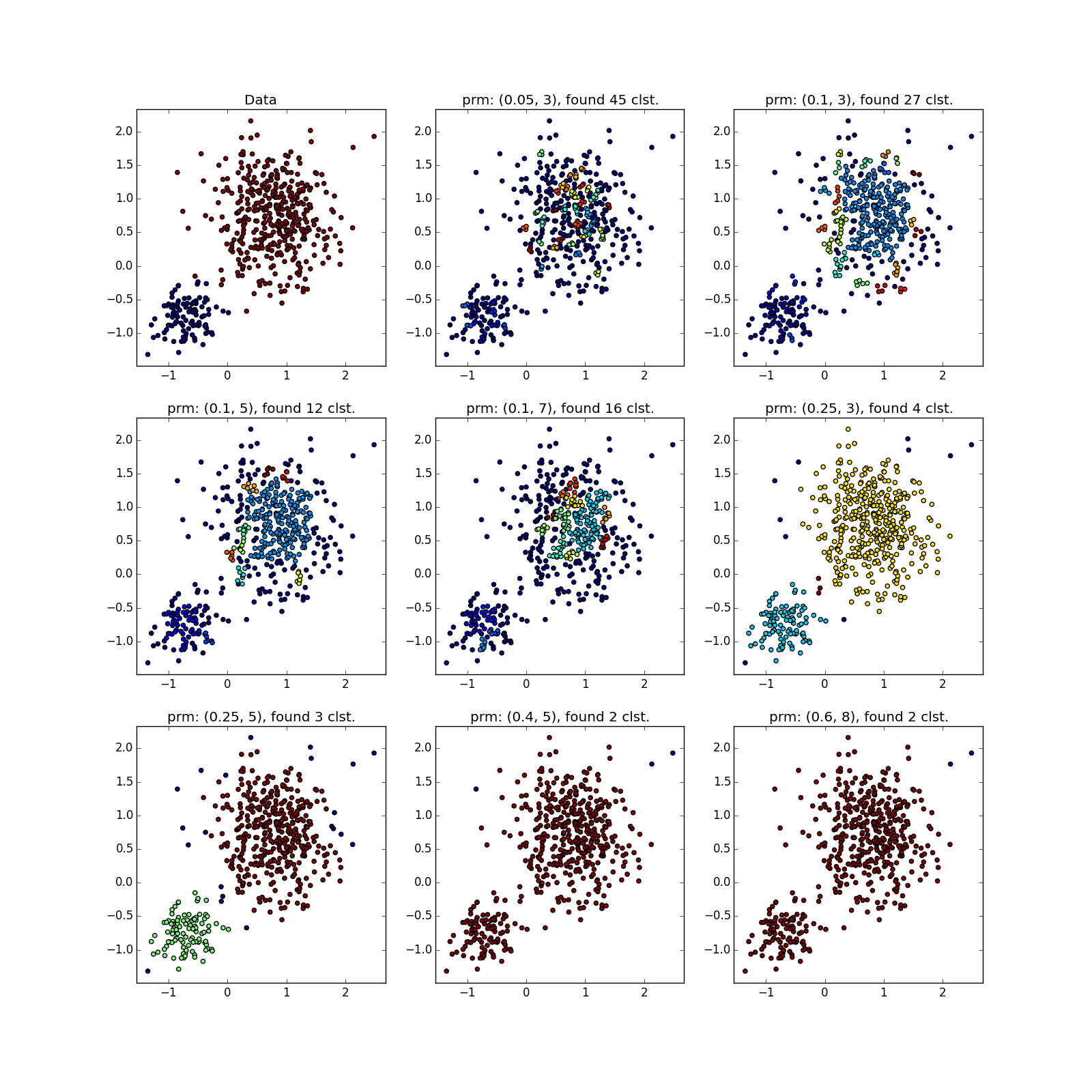
...データが非常にうるさい場合でも。 ここで、DBSCANには、クラスターごとに非対称に分散された放出を簡単に受け入れることができるk-meansよりも利点があります。
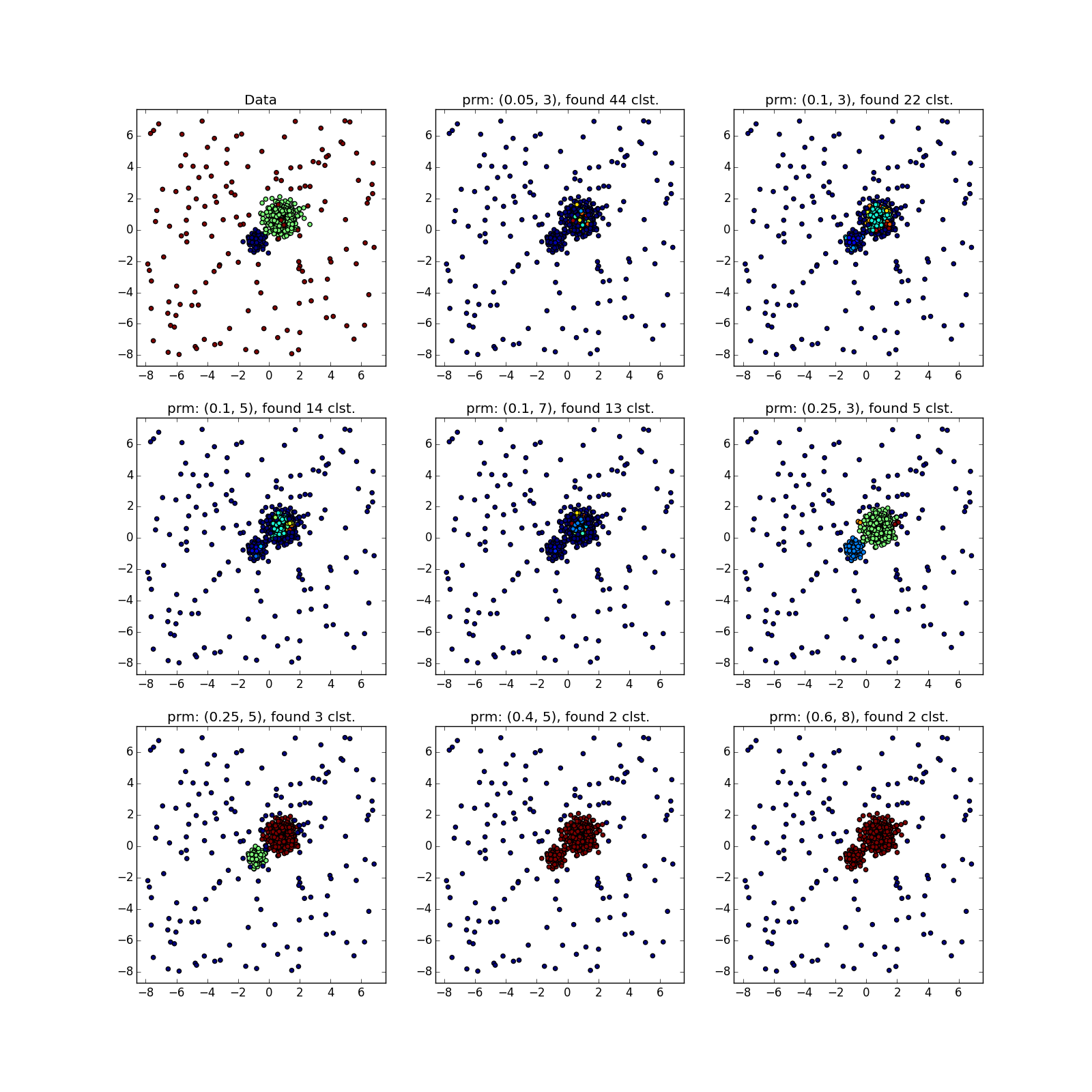
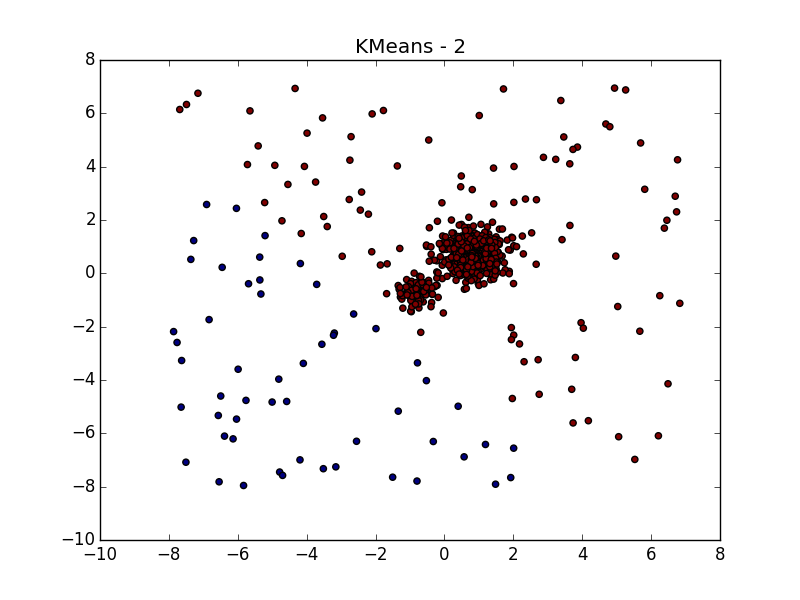
しかし、異なる密度のクラスターでは、すべてがバラ色ではありません。 DBSCANは、より高密度のクラスターのみ、または全体を検出します。
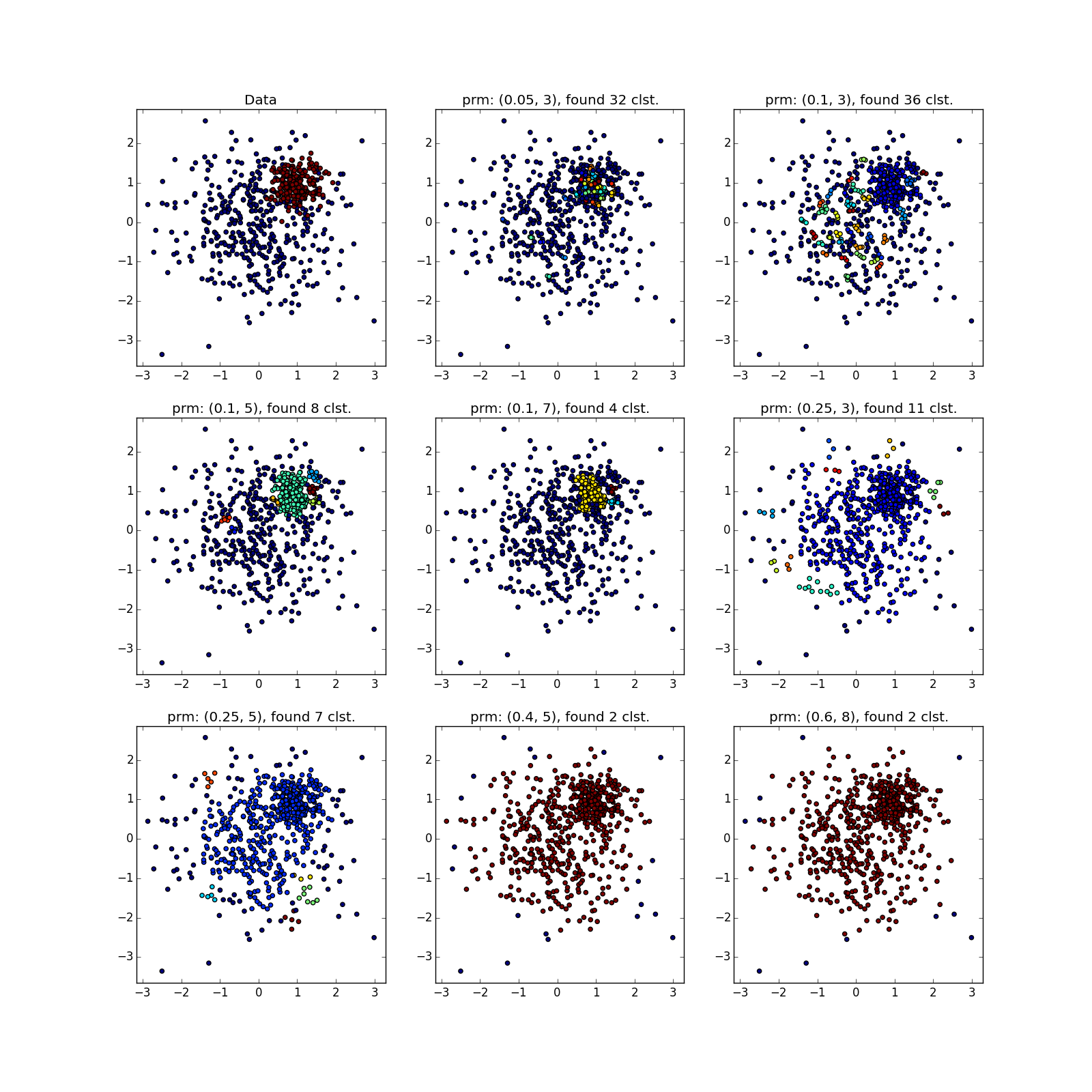
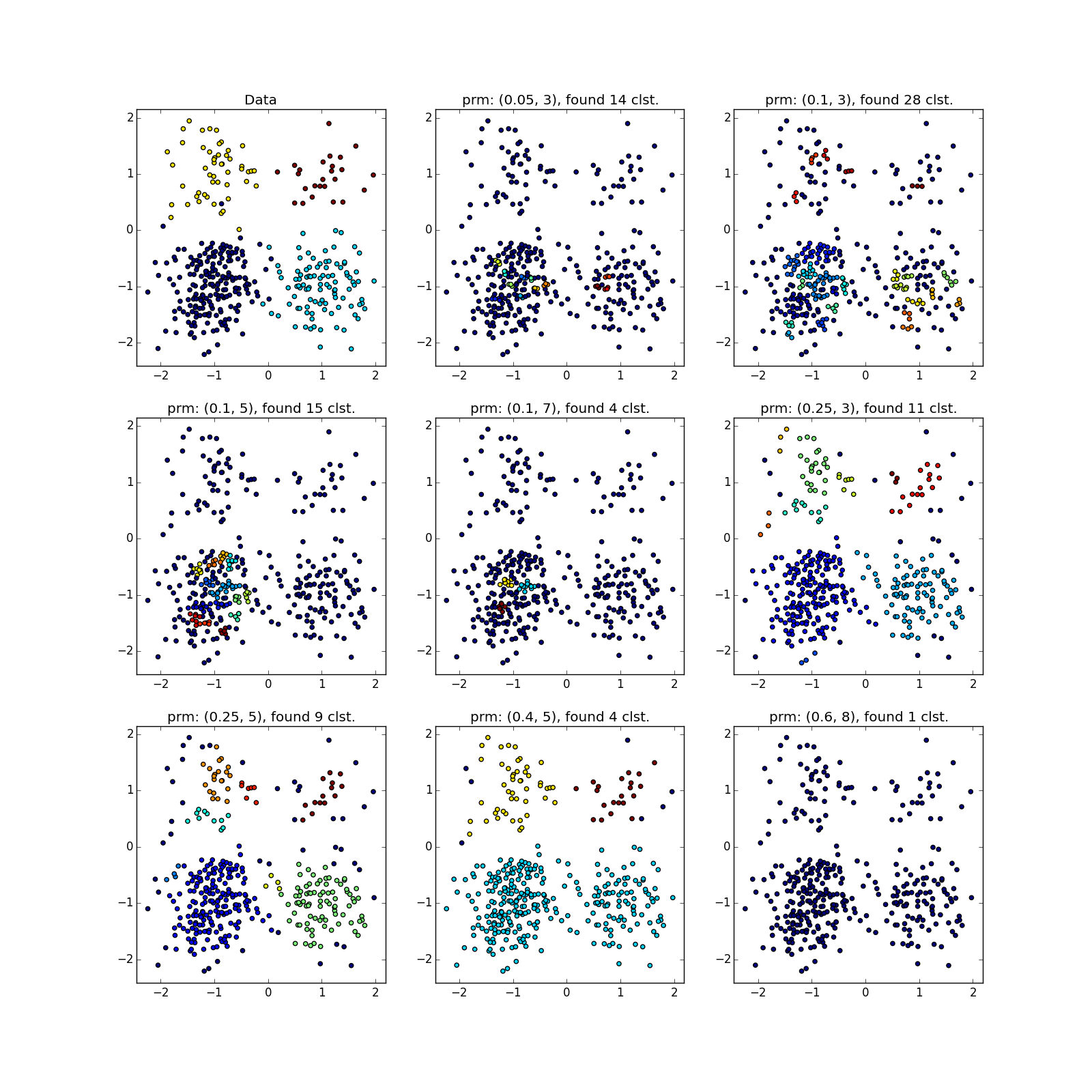
偶然、または異なるパラメーターでDBSCANを数回実行しない限り、疑わしいものを見ることができます。 実際-アルゴリズムの種類の手動実行。
より複雑なディストリビューションでは、幸運です。 それらが互いに十分に分離できる場合、DBSCANは機能します。 (0.4、5)-優れたパーティションを参照してください。ただし、アルゴリズムで外れ値と見なされるポイントが多すぎます。

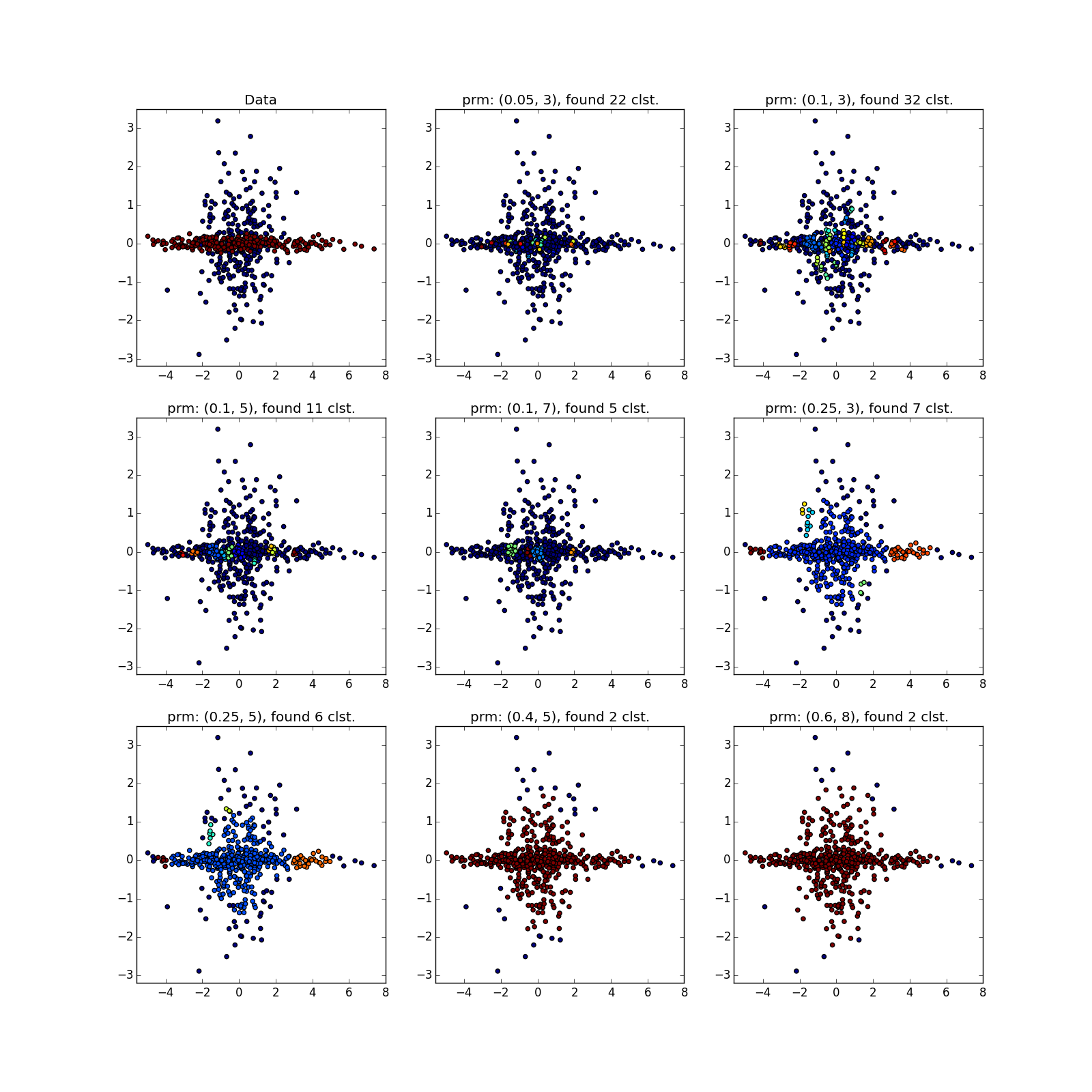
ジャンパーが優先される場合、実際にはそうではありません。 選択した場所に多くのポイントが蓄積されたため、DBSCANは明らかに異なる分布の「花びら」を区別できません。
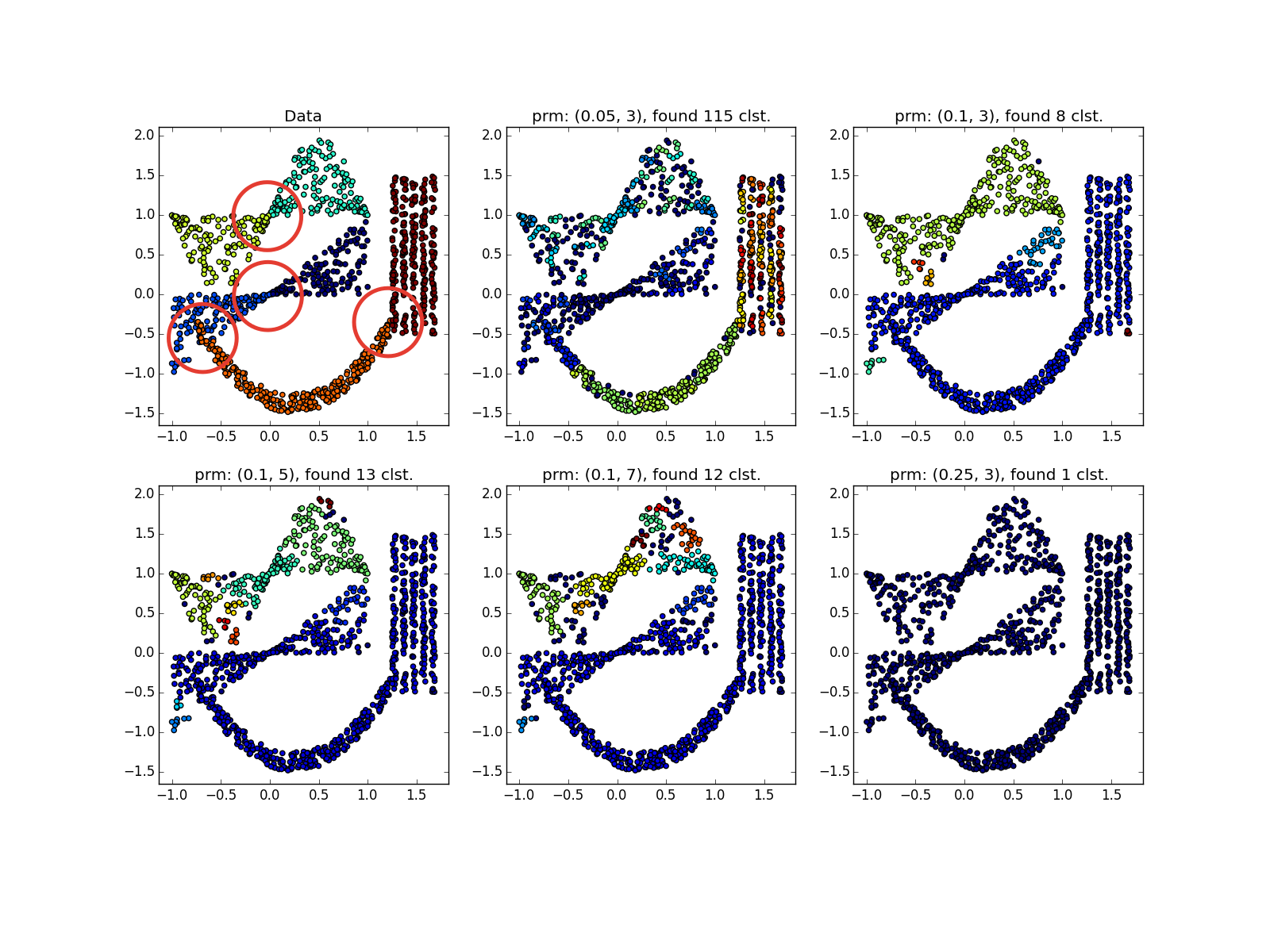
DBSCANは、高密度で十分に分離されたクラスターで優れた機能を発揮します。 さらに、その形状はまったく重要ではありません。 おそらく、DBSCANは、小さなクラスターの検出において、すべての非専門アルゴリズムよりも優れています。



4行の例では、パラメーターに応じて、行のギャップにより8クラスターと4クラスターの両方を取得できることに注意してください。 一般的に、これは望ましい動作です-分布が正しいかどうか、または単に十分なデータがないかどうかは不明です。 ここでは幸運でした。線間の距離が開口部のサイズよりも大きいです。 また、スパイラルを使用した例では、どのポイントが異なるクラスターに属しているかに注意してください。 クラスターに割り当てられたスパイラルの長さは、近隣の数の減少とともに増加します。 スパイラルの中心に近いほど、ポイントは密になります。
さまざまなサイズの蓄積が適切に決定されます...

...データが非常にうるさい場合でも。 ここで、DBSCANには、クラスターごとに非対称に分散された放出を簡単に受け入れることができるk-meansよりも利点があります。


しかし、異なる密度のクラスターでは、すべてがバラ色ではありません。 DBSCANは、より高密度のクラスターのみ、または全体を検出します。



偶然、または異なるパラメーターでDBSCANを数回実行しない限り、疑わしいものを見ることができます。 実際-アルゴリズムの種類の手動実行。
より複雑なディストリビューションでは、幸運です。 それらが互いに十分に分離できる場合、DBSCANは機能します。 (0.4、5)-優れたパーティションを参照してください。ただし、アルゴリズムで外れ値と見なされるポイントが多すぎます。

ジャンパーが優先される場合、実際にはそうではありません。 選択した場所に多くのポイントが蓄積されたため、DBSCANは明らかに異なる分布の「花びら」を区別できません。

まとめ
次の場合にDBSCANを使用します。
- 適度に大きい( )データセット。 でも 手元に最適化および並列化された実装がある場合。
- 近接関数は事前に知られており、対称的であり、それほど複雑ではないことが望ましい。 KDツリー最適化は、多くの場合、ユークリッド距離でのみ機能します。
- 入れ子になった異常なクラスター、小さな折り目など、エキゾチックな形式のデータのクラスターが表示されます。
- 房間の境界の密度は、最も密度の低いクラスターの密度よりも低くなります。 クラスターが互いに完全に分離されている場合が望ましいです。
- データセット要素の複雑さは重要ではありません。 ただし、それらは密度に大きなギャップがないように十分でなければなりません(前の段落を参照)。
- クラスタ内の要素の数は任意に変えることができます。
- 排出量が大規模に分散している場合、排出量は問題になりません(合理的な範囲内)。
- クラスターの数は関係ありません。
DBSCANには、成功したアプリケーションの歴史があります。 たとえば、タスクでの使用に注意できます。
これで、サイクルの2番目の部分を完了したいと思います。 この記事がお役に立てば幸いです。そして、データ分析タスクでDBSCANを試してみるべきときと、使用すべきでないときを知っているようになりました。