Clever Geek Handbook

テンソルフローの熱伝導方程式

こんにちは、Habr！ 少し前に、私はディープラーニングに興味を持ち、ゆっくりとテンソルフローの研究を始めました。 テンソルフローを掘り下げながら、私は並列プログラミングのコースを思い出しました。それは大学の4年目にその年に行いました。 そこでのタスクは次のように策定されました。



2次元熱方程式の線形初期境界値問題：



\ frac {\ partial u} {\ partial t} = \ sum \ limits _ {\ alpha = 1} ^ {2} \ frac {\ partial} {\ partial x_ \ alpha} \ left（k_ \ alpha \ frac {\部分u} {\部分x_ \ alpha} \右）-u、\ quad x_ \ alpha \ in [0,1] \ quad（\ alpha = 1,2）、\ t＆gt; 0;






k_ \ alpha = \ begin {cases} 50、（x_1、x_2）\ in \ Delta ABC \\ 1、（x_1、x_2）\ notin \ Delta ABC \ end {cases}






（\ alpha = 1,2）、\ A（0.2、0.5）、\ B（0.7、0.2）、\ C（0.5、0.8）;






u（x_1、x_2、0）= 0、\ u（0、x_2、t）= 1-e ^ {-\ omega t}、\ u（1、x_2、t）= 0、






u（x_1,0、t）= 1-e ^ {-\ omega t}、\ u（0、x_2、t）= 0、\ \ omega = 20






これを拡散方程式と呼ぶ方が正しいでしょうが。



次に、並列化にMPIを使用し、共役勾配法を使用して、暗黙的なスキームの有限差分法によってタスクを解決する必要がありました。



私はまだ数値法の専門家ではなく、テンソルフローの専門家でもありませんが、すでに経験を積んでいます。 そして、私はディープラーニングのフレームワークに関する教訓を計算しようと熱望していました。 共役勾配法をもう一度実装するのは面白くありませんが、テンソルフローが計算をどのように処理し、どのような困難が生じるかを見るのは面白くなります。 この投稿は、その由来についてです。



数値アルゴリズム





グリッドを定義します。

\ Omega = \ omega_ {x_1} \ times \ omega_ {x_2} \ times \ omega_t、






\ [\ omega_ {x_ \ alpha} = \ left \ {x _ {\ alpha、i_ \ alpha} = i_ \ alpha h、i_ \ alpha = 0、...、N、h = \ frac {1} {N }、\ right \} \ \ alpha = 1,2、\]






\ [\ omega_t = \ left \ {t_j = j \ tau、j = 0、...、N_t、\ tau = \ frac {t_ {max}} {N_t} \ right \}






差分スキーム：



ペイントを簡単にするために、演算子を導入します：



\ Delta_ {1} f_ {i、j} = \ frac {f_ {i + 1/2、j}-f_ {i-1 / 2、j}} {h}、






\ Delta_ {2} f_ {i、j} = \ frac {f_ {i、j + 1/2}-f_ {i、j-1 / 2}} {h}。






明示的な差分スキーム：



\ frac {u_ {i、j} ^ t-u_ {i、j} ^ {t-1}} {\ tau} = \ Delta_ {1}（k_ {i、j} \ Delta_ {1} u_ {i 、j} ^ {t-1}）+ \ Delta_ {2}（k_ {i、j} \ Delta_ {2} u_ {i、j} ^ {t-1}）-u_ {i、j} ^ t 。






明示的な差分スキームの場合、前の瞬間の関数の値が計算に使用され、方程式を解く必要はありません。 u ^ t_ {i、j} 。 ただし、このようなスキームは精度が低く、必要なタイムステップが大幅に小さくなります。



暗黙的な差分スキーム：



\ frac {u_ {i、j} ^ t-u_ {i、j} ^ {t-1}} {\ tau} = \ Delta_ {1}（k_ {i、j} \ Delta_ {1} u_ {i 、j} ^ t）+ \ Delta_ {2}（k_ {i、j} \ Delta_ {2} u_ {i、j} ^ t）-u_ {i、j} ^ t、






\ frac {u_ {i、j} ^ t-u_ {i、j} ^ {t-1}} {\ tau} = \ Delta_ {1}（k_ {i、j} \ frac {u_ {i + 1 / 2、j} ^ t-u_ {i-1 / 2、j} ^ t} {h}）+ \ Delta_ {2}（k_ {i、j} \ frac {u_ {i、j + 1/2 } ^ t-u_ {i、j-1 / 2} ^ t} {h}）-u_ {i、j} ^ t、






\ frac {u_ {i、j} ^ t-u_ {i、j} ^ {t-1}} {\ tau} = \ frac {k_ {i + 1/2、j} \ frac {u_ {i + 1、j} ^ t-u_ {i、j} ^ t} {h}-k_ {i-1 / 2、j} \ frac {u_ {i、j} ^ t-u_ {i-1 / 2、 j} ^ t} {h}} {h} + \ frac {k_ {i、j + 1/2} \ frac {u_ {i、j + 1} ^ t-u_ {i、j} ^ t} { h}-k_ {i、j-1 / 2} \ frac {u_ {i、j} ^ t-u_ {i、j-1 / 2} ^ t} {h}} {h}-u_ {i、 j} ^ t、






\ frac {u_ {i、j} ^ t-u_ {i、j} ^ {t-1}} {\ tau} = \ frac {k_ {i + 1/2、j} u_ {i + 1、j } ^ t-u_ {i、j} ^ t-k_ {i-1 / 2、j} u_ {i、j} ^ t-u_ {i-1 / 2、j} ^ t + k_ {i、j +1/2} u_ {i、j + 1} ^ t-u_ {i、j} ^ t-k_ {i、j-1 / 2} u_ {i、j} ^ t-u_ {i、j- 1/2} ^ t} {h ^ 2}-u_ {i、j} ^ t。






関連するすべてを左に移動します u ^ t 、そして右へ u ^ {t-1} そして乗算する \タウ ：



（1 + \ frac {\ tau} {h ^ 2}（k_ {i + 1/2、j} + k_ {i-1 / 2、j} + k_ {i、j + 1/2} + k_ { i、j-1 / 2}）+ \ tau）u_ {i、j} ^ t-\\-\ frac {\ tau} {h ^ 2}（k_ {i + 1/2、j} u_ {i + 1、j} ^ t + k_ {i-1 / 2、j} u ^ t_ {i-1、j} + k_ {i、j + 1/2} u ^ t_ {i、j + 1} + k_ {i、j-1 / 2} u ^ t_ {i、j-1}）= u ^ {t-1} _ {i、j}。






実際、グリッド上で演算子方程式を取得しました。



Au ^ t = u ^ {t-1}、






値を書くとどうなる u ^ t 通常のベクトルとしてのグリッドノードでは、線形方程式の通常のシステム（ Ax = b ） 前回の値は既に計算されているため、定数です。

便宜上、演算子を提示します A 2つの演算子の違いとして：



A = D_A-（A ^ + + A ^ {-}）、






ここで：



D_A u ^ t =（1 + \ frac {\ tau} {h ^ 2}（k_ {i + 1/2、j} + k_ {i-1 / 2、j} + k_ {i、j + 1 / 2} + k_ {i、j-1 / 2}）+ \ tau）u ^ t_ {i、j}、






（A ^ + + A ^ {-}）u ^ t = \ frac {\ tau} {h ^ 2}（k_ {i + 1/2、j} u ^ t_ {i + 1、j} + k_ { i-1 / 2、j} u ^ t_ {i-1、j} + k_ {i、j + 1/2} u ^ t_ {i、j + 1} + k_ {i、j-1 / 2} u ^ t_ {i、j-1}）。






交換 u ^ t 評価に \ hat {u} ^ t 、エラー関数を書きます：



r = A \ hat {u} ^ t-u ^ {t-1} =（D_A-A ^ +-A ^ {-}）\ hat {u} ^ t-u ^ {t-1}、






L = \ sum r_ {i、j} ^ 2。






どこで r_ {i、j} -グリッドノードのエラー。



勾配を使用して、汎関数誤差を繰り返し最小化します。



その結果、タスクはテンソルと勾配降下の乗算に削減されました。これがまさにテンソルフローの目的です。



Tensorflowの実装



テンソルフローについて簡単に



テンソルフローでは、最初に計算グラフが作成されます。 グラフのリソースはtf.Session内で割り当てられます 。 グラフノードはデータ操作です。 グラフへの入力のセルはtf.placeholderです。 グラフを実行するには、セッションオブジェクトでrunメソッドを実行し、目的の操作とプレースホルダーの入力データを渡します。 runメソッドは操作の結果を返し、セッション内のtf.Variable内の値を変更することもできます。



tensorflow自体は、元のグラフに勾配が実装されている操作のみが含まれている場合（まだではない場合）、勾配backpropagationを実装する操作のグラフを作成できます。



コード：



最初に初期化コード。 ここでは、すべての予備操作を実行し、事前に計算できるすべてのものを検討します。



初期化 
#  import numpy as np import pandas as pd import tensorflow as tf import matplotlib.pyplot as plt import matplotlib from matplotlib.animation import FuncAnimation from matplotlib import cm import seaborn #    ,   #     class HeatEquation(): def __init__(self, nxy, tmax, nt, k, f, u0, u0yt, u1yt, ux0t, ux1t): self._nxy = nxy #    x, y self._tmax = tmax #   self._nt = nt #    self._k = k #  k self._f = f #  f self._u0 = u0 #   #   self._u0yt = u0yt self._u1yt = u1yt self._ux0t = ux0t self._ux1t = ux1t #       self._h = h = np.array(1./nxy) self._ht = ht = np.array(tmax/nt) print("ht/h/h:", ht/h/h) self._xs = xs = np.linspace(0., 1., nxy + 1) self._ys = ys = np.linspace(0., 1., nxy + 1) self._ts = ts = np.linspace(0., tmax, nt + 1) from itertools import product #       self._vs = vs = np.array(list(product(xs, ys)), dtype=np.float64) #   self._vcs = vsc = np.array(list(product(xs[1:-1], ys[1:-1])), dtype=np.float64) #      k vkxs = np.array(list(product((xs+h/2)[:-1], ys)), dtype=np.float64) # k_i+0.5,j vkys = np.array(list(product(xs, (ys+h/2)[:-1])), dtype=np.float64) # k_i ,j+0.5 #    k self._kxs = kxs = k(vkxs).reshape((nxy,nxy+1)) self._kys = kys = k(vkys).reshape((nxy+1,nxy)) #   D_A D_A = np.zeros((nxy+1, nxy+1)) D_A[0:nxy+1,0:nxy+0] += kys D_A[0:nxy+1,1:nxy+1] += kys D_A[0:nxy+0,0:nxy+1] += kxs D_A[1:nxy+1,0:nxy+1] += kxs self._D_A = D_A = 1 + ht/h/h*D_A[1:nxy,1:nxy] + ht # ,    self._U_shape = (nxy+1, nxy+1, nt+1) #        , #    ,     self._U = np.zeros(self._U_shape) #       self._U[:,:,0] = u0(vs).reshape(self._U_shape[:-1])




\タウ そして h そのように取られるべきです \ frac {\ tau} {h ^ 2} 特に「非平滑」機能を使用する場合は、小さく、できれば少なくとも1未満でした。



方程式のグラフを作成する方法：



計算グラフ 
 # ,   def build_graph(self, learning_rate): def reset_graph(): if 'sess' in globals() and sess: sess.close() tf.reset_default_graph() reset_graph() nxy = self._nxy #   kxs_ = tf.placeholder_with_default(self._kxs, (nxy,nxy+1)) kys_ = tf.placeholder_with_default(self._kys, (nxy+1,nxy)) D_A_ = tf.placeholder_with_default(self._D_A, self._D_A.shape) U_prev_ = tf.placeholder(tf.float64, (nxy+1, nxy+1), name="U_t-1") f_ = tf.placeholder(tf.float64, (nxy-1, nxy-1), name="f") #      ,     U_ = tf.Variable(U_prev_, trainable=True, name="U_t", dtype=tf.float64) #   def s(tensor, frm): return tf.slice(tensor, frm, (nxy-1, nxy-1)) #    A+_A-  u Ap_Am_U_ = s(U_, (0, 1))*s(self._kxs, (0, 1)) Ap_Am_U_ += s(U_, (2, 1))*s(self._kxs, (1, 1)) Ap_Am_U_ += s(U_, (1, 0))*s(self._kys, (1, 0)) Ap_Am_U_ += s(U_, (1, 2))*s(self._kys, (1, 1)) Ap_Am_U_ *= self._ht/self._h/self._h #  res = D_A_*s(U_,(1, 1)) - Ap_Am_U_ - s(U_prev_, (1, 1)) - self._ht*f_ #  ,    loss = tf.reduce_sum(tf.square(res), name="loss_res") #         u0yt_ = None u1yt_ = None ux0t_ = None ux1t_ = None if self._u0yt: u0yt_ = tf.placeholder(tf.float64, (nxy+1,), name="u0yt") loss += tf.reduce_sum(tf.square(tf.slice(U_, (0, 0), (1, nxy+1)) - tf.reshape(u0yt_, (1, nxy+1))), name="loss_u0yt") if self._u1yt: u1yt_ = tf.placeholder(tf.float64, (nxy+1,), name="u1yt") loss += tf.reduce_sum(tf.square(tf.slice(U_, (nxy, 0), (1, nxy+1)) - tf.reshape(u1yt_, (1, nxy+1))), name="loss_u1yt") if self._ux0t: ux0t_ = tf.placeholder(tf.float64, (nxy+1,), name="ux0t") loss += tf.reduce_sum(tf.square(tf.slice(U_, (0, 0), (nxy+1, 1)) - tf.reshape(ux0t_, (nxy+1, 1))), name="loss_ux0t") if self._ux1t: ux1t_ = tf.placeholder(tf.float64, (nxy+1,), name="ux1t") loss += tf.reduce_sum(tf.square(tf.slice(U_, (0, nxy), (nxy+1, 1)) - tf.reshape(ux1t_, (nxy+1, 1))), name="loss_ux1t") #  ,        , #   ,    loss /= (nxy+1)*(nxy+1) #    train_step = tf.train.AdamOptimizer(learning_rate, 0.7, 0.97).minimize(loss) #     ,    self.g = dict( U_prev = U_prev_, f = f_, u0yt = u0yt_, u1yt = u1yt_, ux0t = ux0t_, ux1t = ux1t_, U = U_, res = res, loss = loss, train_step = train_step ) return self.g




良い方法では、与えられたエッジで関数の値を考慮し、内部領域でのみ関数の値を最適化する必要がありましたが、これには問題が生じました。 テンソルの一部のみを最適化できるようにする方法はなく、勾配の割り当ては（投稿を書いている時点で）テンソルスライスの値の割り当て操作に対して書き込まれていません。 エッジをトリッキーに調整したり、独自のオプティマイザーを作成したりできます。 ただし、関数値の境界と境界条件の差をエラー関数に追加するだけでうまく機能します。



誤差汎関数が2次であっても、適応モーメントを使用した方法が最適であることが判明したことは注目に値します。



関数の計算 ：各時点で、maxiterを超えるか、エラーがeps未満になるまで、最適化を数回繰り返し、保存して次の瞬間に進みます。



計算 
 def train_graph(self, eps, maxiter, miniter): g = self.g losses = [] #    with tf.Session() as sess: #       sess.run(tf.global_variables_initializer(), feed_dict=self._get_graph_feed(0)) for t_i, t in enumerate(self._ts[1:]): t_i += 1 losses_t = [] losses.append(losses_t) d = self._get_graph_feed(t_i) p_loss = float("inf") for i in range(maxiter): #     #    u,   _, self._U[:,:,t_i], loss = sess.run([g["train_step"], g["U"], g["loss"]], feed_dict=d) losses_t.append(loss) if i > miniter and abs(p_loss - loss) < eps: p_loss = loss break p_loss = loss print('#', end="") return self._U, losses




打ち上げ：



起動コード 
 tmax = 0.5 nxy = 100 nt = 10000 A = np.array([0.2, 0.5]) B = np.array([0.7, 0.2]) C = np.array([0.5, 0.8]) k1 = 1.0 k2 = 50.0 omega = 20 #     def triang(v, k1, k2, A, B, C): v_ = v.copy() k = k1*np.ones([v.shape[0]]) v_ = v - A B_ = B - A C_ = C - A m = (v_[:, 0]*B_[1] - v_[:, 1]*B_[0]) / (C_[0]*B_[1] - C_[1]*B_[0]) l = (v_[:, 0] - m*C_[0]) / B_[0] inside = (m > 0.) * (l > 0.) * (m + l < 1.0) k[inside] = k2 return k # 0.0 def f(v, t): return 0*triang(v, h0, h1, A, B, C) # 0.0 def u0(v): return 0*triang(v, t1, t2, A, B, C) #   def u0ytb(t, ys): return 1 - np.exp(-omega*np.ones(ys.shape[0])*t) def ux0tb(t, xs): return 1 - np.exp(-omega*np.ones(xs.shape[0])*t) def u1ytb(t, ys): return 0.*np.ones(ys.shape[0]) def ux1tb(t, xs): return 0.*np.ones(xs.shape[0]) #     eq = HeatEquation(nxy, tmax, nt, lambda x: triang(x, k1, k2, A, B, C), f, u0, u0ytb, u1ytb, ux0tb, ux1tb) _ = eq.build_graph(0.001) U, losses = eq.train_graph(1e-6, 100, 1)




結果



元の状態：



非表示のテキスト






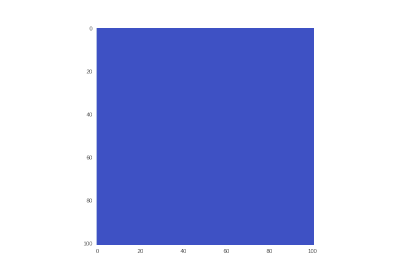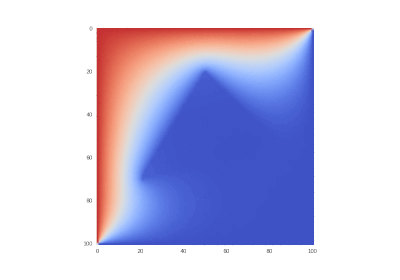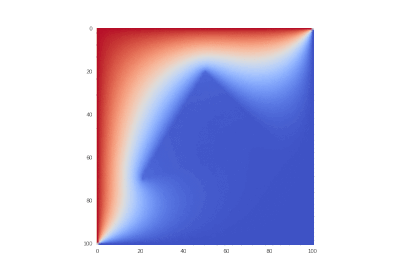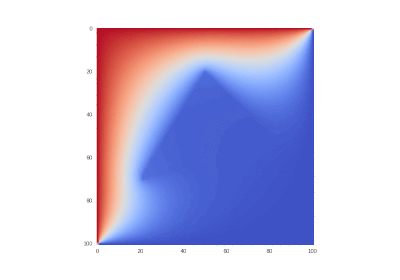
オリジナルとしての条件、ただしなし -u 方程式では：



非表示のテキスト
\ frac {\ partial u} {\ partial t} = \ sum \ limits _ {\ alpha = 1} ^ {2} \ frac {\ partial} {\ partial x_ \ alpha} \ left（k_ \ alpha \ frac {\部分u} {\部分x_ \ alpha} \右）、\ quad x_ \ alpha \ in [0,1] \ quad（\ alpha = 1,2）、\ t＆gt; 0;






k_ \ alpha = \ begin {cases} 50、（x_1、x_2）\ in \ Delta ABC \\ 1、（x_1、x_2）\ notin \ Delta ABC \ end {cases}






u（x_1、x_2、0）= 0、\ u（0、x_2、t）= 1-e ^ {-\ omega t}、\ u（1、x_2、t）= 0、






u（x_1,0、t）= 1-e ^ {-\ omega t}、\ u（0、x_2、t）= 0、\ \ omega = 20






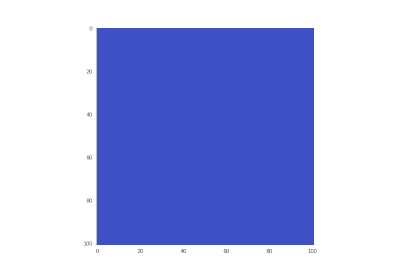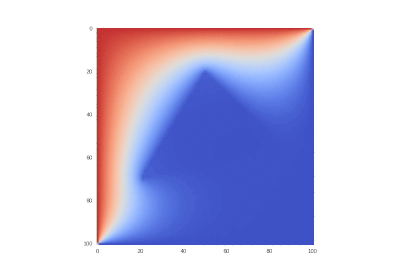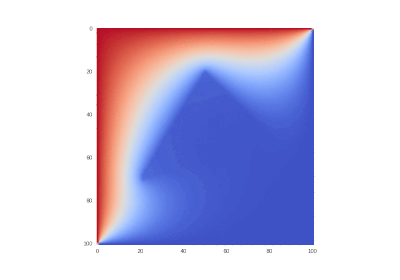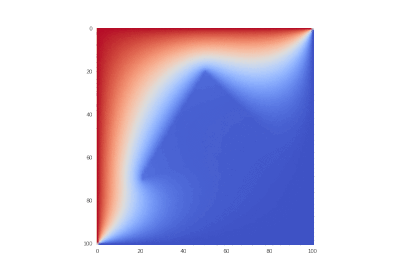
コードで簡単に修正されます： 



 #   __init__ self._D_A = D_A = 1 + ht/h/h*D_A[1:nxy,1:nxy]


デリバティブは関数自体よりも高次であるため、ほとんど違いはありません。









さらにどこでも：



\ frac {\ partial u} {\ partial t} = \ sum \ limits _ {\ alpha = 1} ^ {2} \ frac {\ partial} {\ partial x_ \ alpha} \ left（k_ \ alpha \ frac {\部分u} {\部分x_ \ alpha} \右）+ f、\ quad x_ \ alpha \ in [0,1] \ quad（\ alpha = 1,2）、\ t＆gt; 0;








加熱エッジが1つある状態：



非表示のテキスト
k_ \ alpha = \ begin {cases} 10、（x_1、x_2）\ in \ Delta ABC \\ 1、（x_1、x_2）\ notin \ Delta ABC \ end {cases}






f（x_1、x_2、t）= 0、






u（x_1、x_2、0）= 0、\ u（0、x_2、t）= 1-e ^ {-\ omega t}、\ u（1、x_2、t）= 0、






u（x_1,0、t）= 0、\ u（0、x_2、t）= 0、\ \ omega = 20














最初に加熱された領域を冷却する条件：



非表示のテキスト
k_ \ alpha = 1






f（x_1、x_2、t）= 0、






u（x_1、x_2、0）= \ begin {cases} 0.1、（x_1、x_2）\ in \ Delta ABC \\ 0、（x_1、x_2）\ notin \ Delta ABC \ end {cases}






u（0、x_2、t）= 0、\ u（1、x_2、t）= 0、






u（x_1,0、t）= 0、\ u（0、x_2、t）= 0














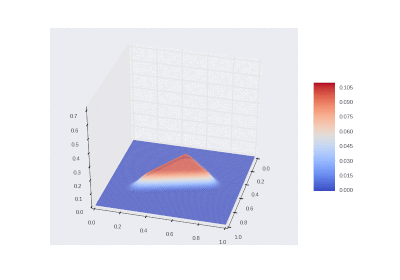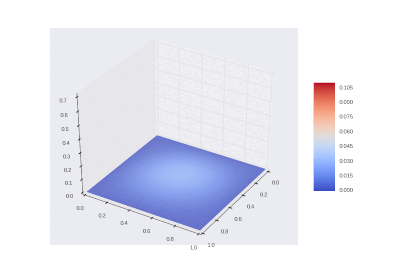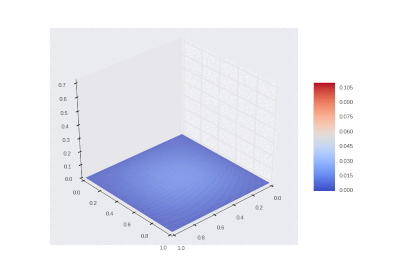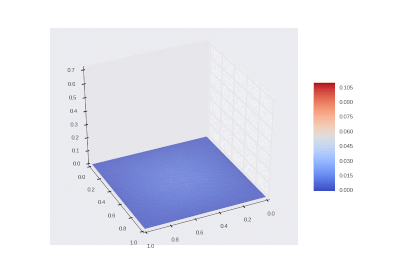
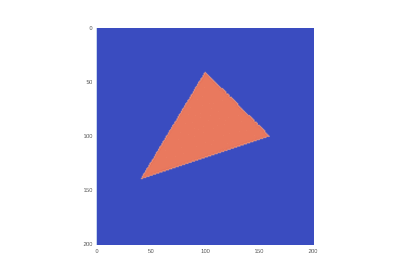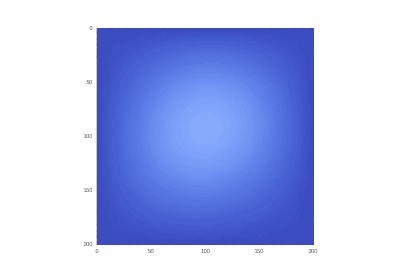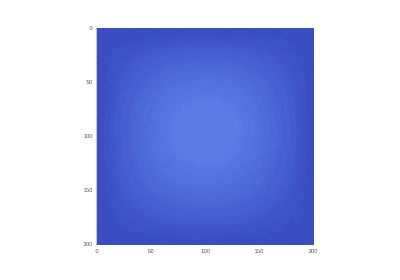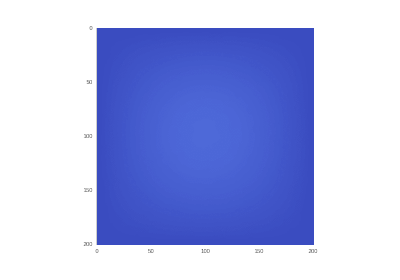
野外での加熱を含む条件：



非表示のテキスト
k_ \ alpha = \ begin {cases} 2、（x_1、x_2）\ in \ Delta ABC \\ 10、（x_1、x_2）\ notin \ Delta ABC \ end {cases}






f（x_1、x_2、t）= \ begin {cases} 10、（x_1、x_2）\ in \ Delta ABC \\ 0、（x_1、x_2）\ notin \ Delta ABC \ end {cases}






u（x_1、x_2、0）= 0、\ u（0、x_2、t）= 0、\ u（1、x_2、t）= 0、






u（x_1,0、t）= 0、\ u（0、x_2、t）= 0














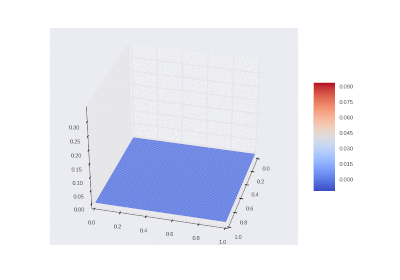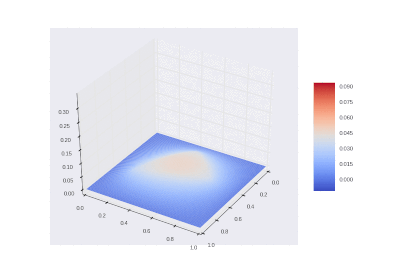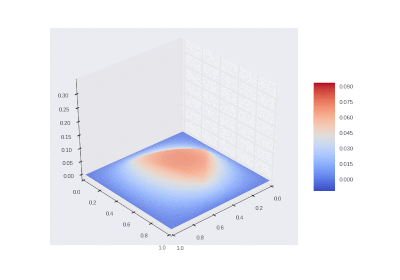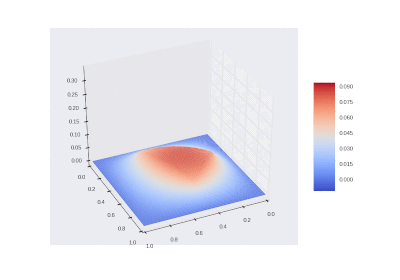
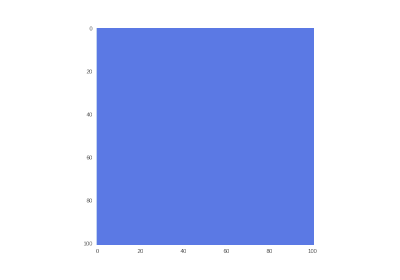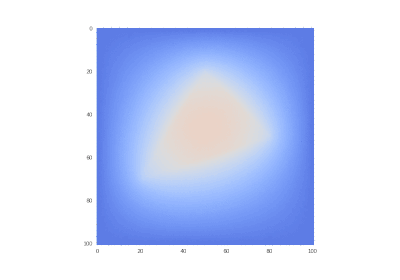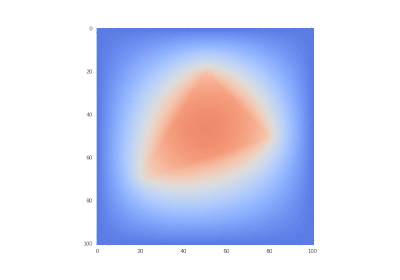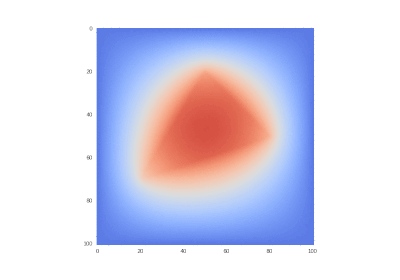
GIF描画



3D GIF関数：



3D GIF
メインクラスで、Uをpandas.DataFrameとして返すメソッドを追加します。 



 def get_U_as_df(self, step=1): nxyp = self._nxy + 1 nxyp2 = nxyp**2 Uf = self._U.reshape((nxy+1)**2,-1)[:, ::step] data = np.hstack((self._vs, Uf)) df = pd.DataFrame(data, columns=["x","y"] + list(range(len(self._ts))[0::step])) return df
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     


 def make_gif(Udf, fname): from mpl_toolkits.mplot3d import Axes3D from matplotlib.ticker import LinearLocator, FormatStrFormatter from scipy.interpolate import griddata fig = plt.figure(figsize=(10,7)) ts = list(Udf.columns[2:]) data = Udf #    ,    matplotlib x1 = np.linspace(data['x'].min(), data['x'].max(), len(data['x'].unique())) y1 = np.linspace(data['y'].min(), data['y'].max(), len(data['y'].unique())) x2, y2 = np.meshgrid(x1, y1) z2s = list(map(lambda x: griddata((data['x'], data['y']), data[x], (x2, y2), method='cubic'), ts)) zmax = np.max(np.max(data.iloc[:, 2:])) + 0.01 zmin = np.min(np.min(data.iloc[:, 2:])) - 0.01 plt.grid(True) ax = fig.gca(projection='3d') ax.view_init(35, 15) ax.set_zlim(zmin, zmax) ax.zaxis.set_major_locator(LinearLocator(10)) ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f')) norm = matplotlib.colors.Normalize(vmin=zmin, vmax=zmax, clip=False) surf = ax.plot_surface(x2, y2, z2s[0], rstride=1, cstride=1, norm=norm, cmap=cm.coolwarm, linewidth=0., antialiased=True) fig.colorbar(surf, shrink=0.5, aspect=5) #       def update(t_i): label = 'timestep {0}'.format(t_i) ax.clear() print(label) surf = ax.plot_surface(x2, y2, z2s[t_i], rstride=1, cstride=1, norm=norm, cmap=cm.coolwarm, linewidth=0., antialiased=True) ax.view_init(35, 15+0.5*t_i) ax.set_zlim(zmin, zmax) return surf, #     anim = FuncAnimation(fig, update, frames=range(len(z2s)), interval=50) anim.save(fname, dpi=80, writer='imagemagick')




2D GIF描画機能：



2D GIF 
 def make_2d_gif(U, fname, step=1): fig = plt.figure(figsize=(10,7)) zmax = np.max(np.max(U)) + 0.01 zmin = np.min(np.min(U)) - 0.01 norm = matplotlib.colors.Normalize(vmin=zmin, vmax=zmax, clip=False) im=plt.imshow(U[:,:,0], interpolation='bilinear', cmap=cm.coolwarm, norm=norm) plt.grid(False) nst = U.shape[2] // step #       def update(i): im.set_array(U[:,:,i*step]) return im #     anim = FuncAnimation(fig, update, frames=range(nst), interval=50) anim.save(fname, dpi=80, writer='imagemagick')




まとめ



GPUを使用しない場合の元の状態は4分26秒、GPUを2分11秒使用すると見なされたことは注目に値します。 ポイントの値が大きいと、ギャップが大きくなります。 ただし、結果のグラフのすべての操作がGPU互換ではありません。



機械の特徴：





次のコードを使用して、どの操作が何に対して実行されるかを確認できます。



非表示のテキスト 
 #    def check_metadata_partitions_graph(self): g = self.g d = self._get_graph_feed(1) with tf.Session() as sess: sess.run(tf.global_variables_initializer(), feed_dict=d) options = tf.RunOptions(output_partition_graphs=True) metadata = tf.RunMetadata() c_val = sess.run(g["train_step"], feed_dict=d, options=options, run_metadata=metadata) print(metadata.partition_graphs)




面白い経験でした。 Tensorflowは、このタスクでうまく機能しました。 たぶん、このアプローチでも何らかの種類のアプリケーションが得られるでしょう-C / C ++よりもPythonでコードを書く方がいいですし、テンソルフローの開発によりさらに簡単になります。



ご清聴ありがとうございました！



中古文学



-Bakhvalov N.S.、Zhidkov N.P.、G.M。Kobelkov Numerical Methods 、2011


More articles:


All Articles