Clever Geek Handbook

楕円曲線に対する因数分解法の有効性の分析。 練習する

因数分解の問題は、RSA暗号強度の定義に直接関連しています。これは、短時間でコードをクラックできる高速な因数分解アルゴリズムが存在しないという仮定に基づいており、しばらくして実行できる場合、データの関連性は失われます。 この記事では、因子分解法の1つについてテストし、結論を導き出します。



因数分解の定義を示します。



整数の因数分解は 、単純な因子の積への分解です。 そのような分解は、算術の基本定理によれば、常に存在し、一意です（因子の順序の精度で）。



分解される数を、文字Nと、乗算の結果としてNを取得する2つの要因によって、aおよびbとして示します。



Lenstra分解アルゴリズム（楕円曲線での分解）は、最速の分解方法の1つです。 Pollard法と多くの共通点がありますが（p-1）、より高速に動作します。これは、サブ指数法であることに注意する必要があります。 アルゴリズムの主な特徴は、因数分解に費やされる時間が次元Nに依存せず、Nの最小除数のサイズに依存することです。



使用されている文献のリストの資料からこの方法の詳細を読むことができますが、それでもアルゴリズムの主要な段階を示しています。



  1. 番号Nを紹介します。
  2. 除数Nの上限であるBの値を選択します。
  3. 0、N-1の整数のセットに属する値であるx、yをランダムに生成します。 これらの値は曲線を定義し、xとyは開始点Pを決定します。
  4. b = y ^ 2-x ^ 3-ax mod nおよびg = N.O.D.（N、4a ^ 3 + 27b ^ 2）を計算します。 gがNに等しくないことが重要です。そうでない場合は、ステップ2に戻ります。 1 <g <nの場合、計算を停止します-除数が見つかりました。 このオプションは、数値Nの小さな値（たとえば、10）で可能です; Nを増やすと、この可能性は少なくなります。
  5. 次に、サイクルを実行する必要があります。その結果、各素数p（2〜B-1の範囲）に対して、ポイントPにp ^ rを掛けます。ここで、rは条件p ^ r <Bを満たす最大次数です。


フィールド演算では、除算はありません。これは、点の座標を見つけるための式で必要なため、式を乗算として変換し、拡張ユークリッドアルゴリズムを使用して逆元を探します。 さらに、数値Nを法とする新しい計算をそれぞれ実行します。



アルゴリズムは、1より大きくN.より小さいN.O.D.（N、P）が見つかったときに作業を完了します。答えの誤りを避けるために、N.O.D。 正の値のみをチェックする必要があります。



異なる数値を因数分解するために必要なタイムラインを考えてください。 （結果は私が書いたプログラムから与えられます）



画像

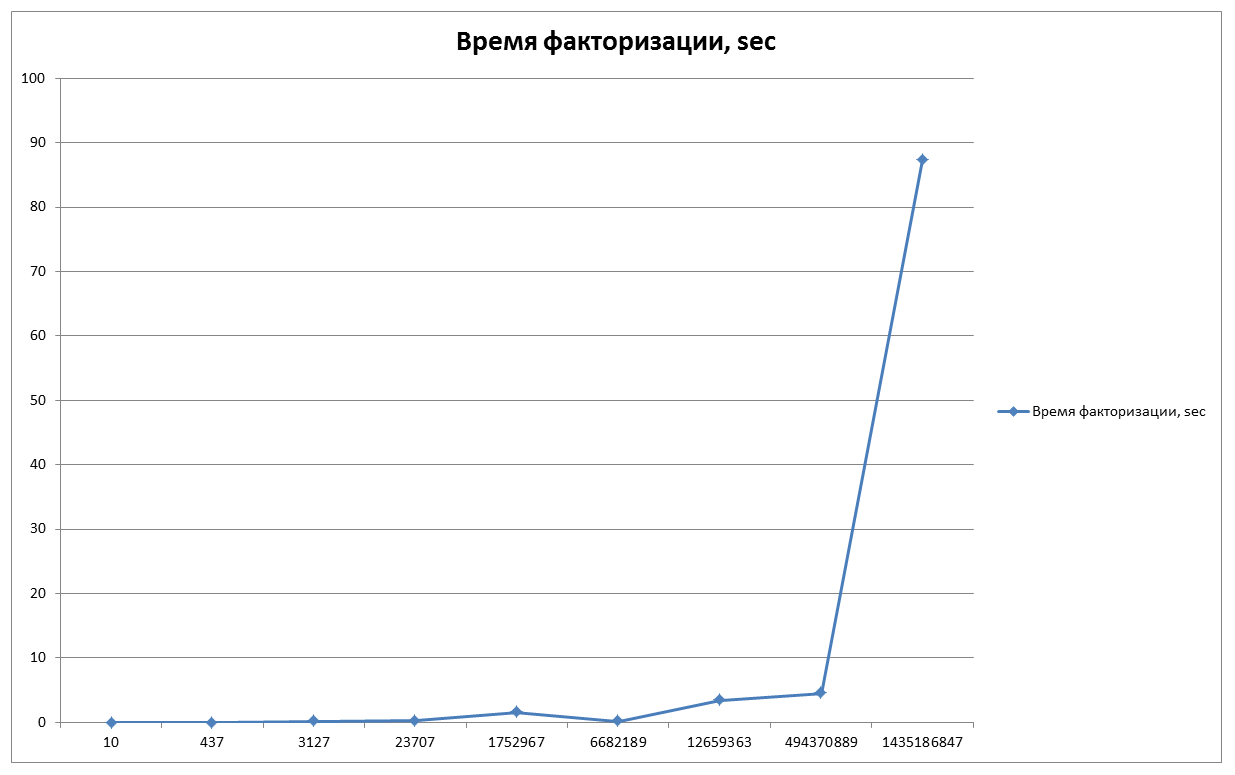
N = 10-0.005秒;

N = 437-0.019秒;

N = 3127-0.055秒;

N = 23707-0.191秒;

N = 1752967-1.53​​4秒;

N = 6682189-0.143秒;

N = 12659363-3.376秒;

N = 494370889-4.484秒;

N = 1435186847-87.377秒;


曲線はランダムな値から生成されるため、新しいプログラムの開始ごとの分解時間は異なります。 曲線が私たちに伝わるかどうかに依存します。 したがって、同じ数値を取得し、さらに数回因数分解して結果を比較しようとします。



画像

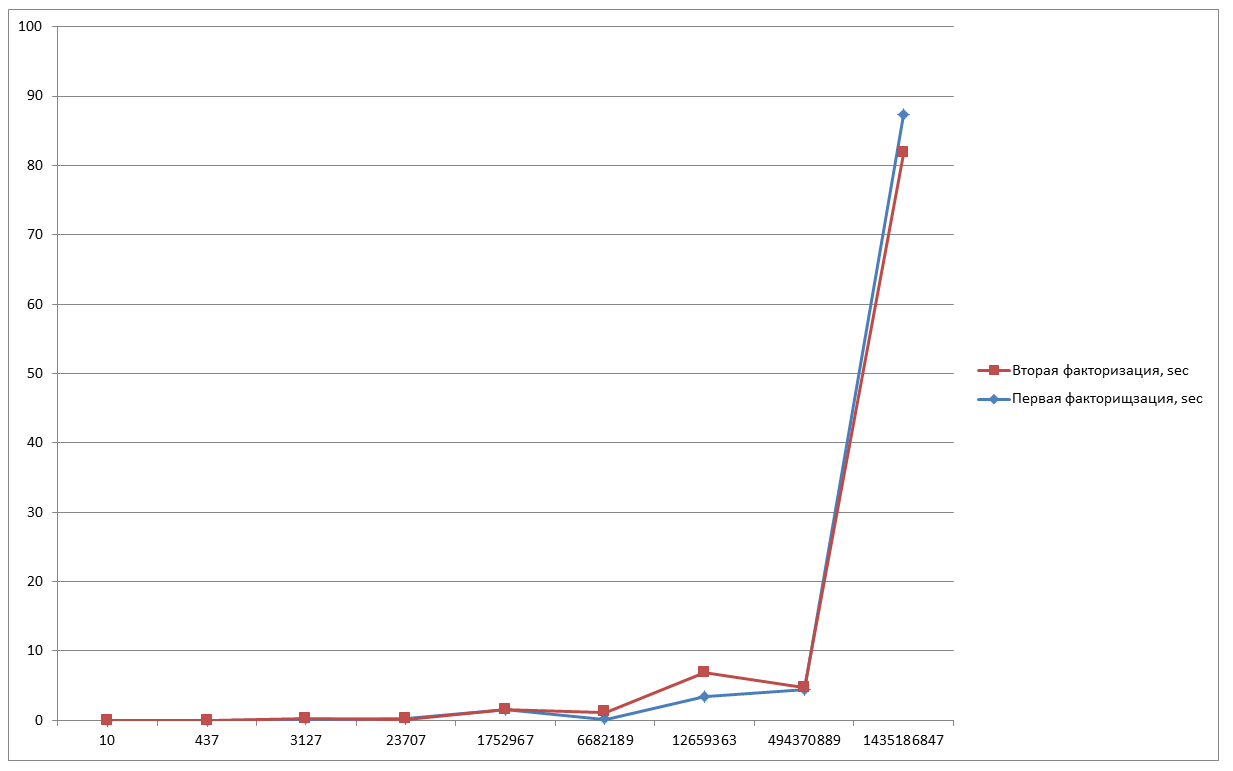
N = 10-0.016秒;

N = 437-0.016秒;

N = 3127-0.218秒;

N = 23707-0.079秒;

N = 1752967-1.484秒;

N = 6682189-1.125秒;

N = 12659363-6.906秒;

N = 494370889-4.781秒;

N = 1435186847-81.766秒;


そして、修正のために最後の測定を行います。



画像

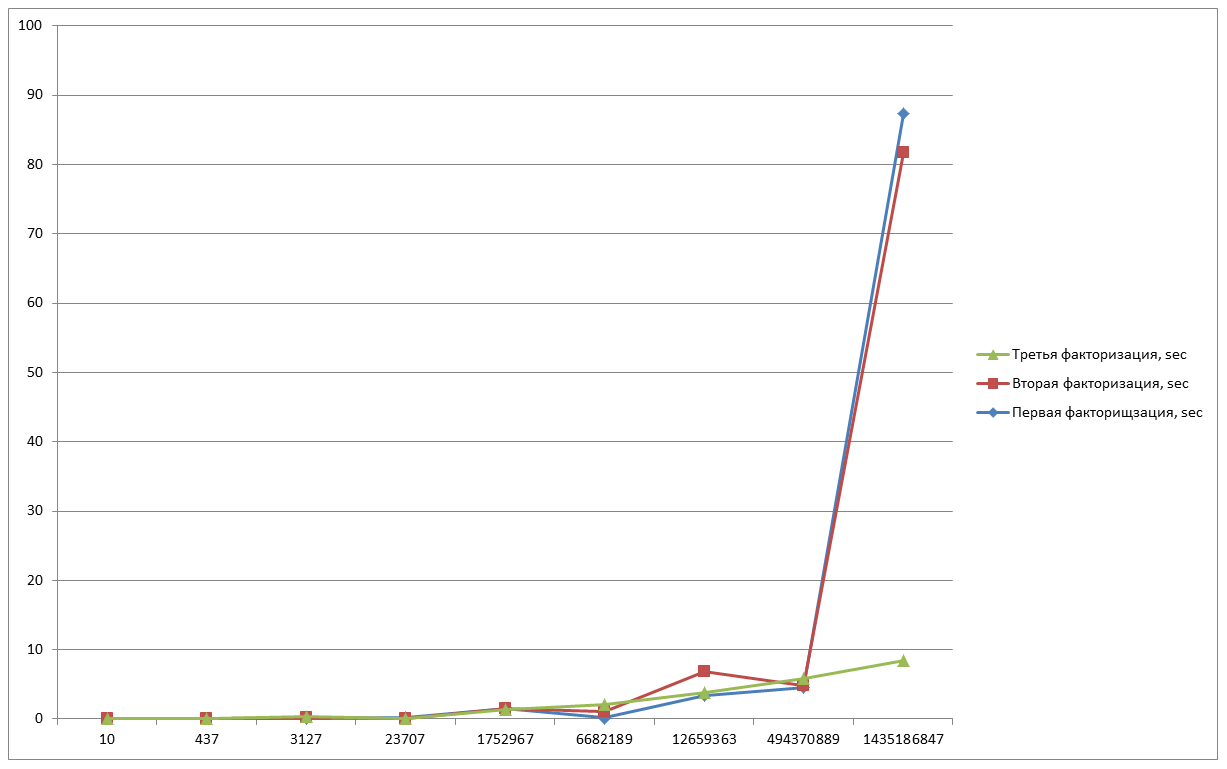
N = 10-0.012秒;

N = 437-0.022秒;

N = 3127-0.156秒;

N = 23707-0.205秒;

N = 1752967-1.418秒;

N = 6682189-1,056秒;

N = 12659363-0.25秒;

N = 494370889-5.488秒;

N = 1435186847-14.117秒;


最後のグラフに見られるように、最後の数に費やされた時間が大幅に減少しました。これは、曲線がランダムに生成されるという事実によって特徴付けられます。 アルゴリズムの実行にかかる時間は、導入するBの値にも依存することに注意してください。 2つの要因（aとb）の値に近い値をとろうとしましたが、初期要因がおおよそでもわからない数で演算を実行する場合は、上記の制限を選択する必要があります。 ただし、制限が高いほど、ポイントの計算に時間がかかります。ポイントが増えるため、これを考慮する必要があります。



コンピューターのパフォーマンスを考慮する必要があります。 周波数3.10 GHzのAMD Athlon（tm）II X4 645プロセッサーで計算しました。 プログラムの実行中は、CPU負荷は約40％でした。 メモリ負荷はありませんでした。



まとめ



アルゴリズムはかなり良い時間動作しますが、比較的小さな値に対してのみです。 結局、グラフ1と2で見られるように、ほとんどの場合10億の後の数字は494370889の数字に費やされた時間と大きなギャップがありますが、これは予想されました。



私の最初の記事を読んでくれてありがとう。



使用文献： 「情報セキュリティの数学的基礎」


More articles:


All Articles