
はじめに
計算グリッドは、有限差分法を使用した数値問題の解決に広く使用されています。 そのようなグリッドを構築する品質がソリューションの成功を大きく左右するため、グリッドが巨大なサイズに達することがあります。 この場合、2つの問題を同時に解決できるため、マルチプロセッサシステムが役立ちます。
- プログラムの速度を上げるため。
- 1つのプロセッサのRAMに収まらないサイズのグリッドを使用します。
このアプローチでは、計算ドメインをカバーするグリッドは多くのドメインに分割され、各ドメインは個別のプロセッサで処理されます。 ここでの主な問題は、パーティションの「誠実さ」です。計算負荷がプロセッサ間で均等に分散される分解を選択する必要があり、計算の重複とプロセッサ間でのデータ転送の必要性によるオーバーヘッドが小さい
2次元計算グリッドの典型的な例を最初の図に示します。 航空機の翼とフラップの周りの空間を記述し、グリッドノードは小さな詳細に凝縮されます。 マルチカラーゾーンのサイズには視覚的な違いがありますが、各ゾーンにはほぼ同じ数のノードが含まれています。 良い分解について話すことができます。 これが解決する問題です。
注:並列ソートはアルゴリズムで積極的に使用されるため、記事を理解するために、「 BatcherマージによるExchange交換ソートネットワーク 」とは何かを知ることを強くお勧めします。
問題の声明
簡単にするために、プロセッサはシングルコアであると想定しています。 もう一度、混乱がないように:
1プロセッサ= 1コア 。 分散メモリを備えたコンピューティングシステムなので、MPIテクノロジを使用します。 実際には、このようなシステムでは、プロセッサはマルチコアです。つまり、スレッドはコンピューティングリソースを最も効率的に使用するためにも使用する必要があります。
グリッドを通常の2次元グリッドのみに制限します。 インデックス(i、j)を持つノードがi、jに存在する隣接ノードに接続されている場合: (i-1、j)、(i + 1、j)、(i、j-1)、(i、j +1) 。 ご覧のように、上の図ではグリッドが規則的ではありません。規則的なグリッドの例を以下に示します。

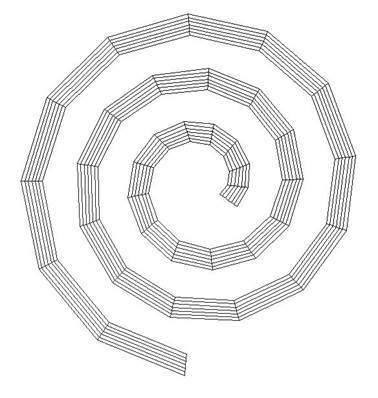
これにより、グリッドトポロジを非常にコンパクトに保存でき、メモリ消費とプログラムランタイムの両方を大幅に削減できます(結局、プロセッサ間でネットワークを介して送信する必要のあるデータは大幅に少なくなります)。
プログラムは、入力に対する3つの引数を受け取ります。
- n1、n2-2次元グリッドの次元。
- kは、グリッドを分割するドメイン(パーツ)の数です。
座標はプログラム内で初期化され、一般的に言えば、どのように発生するかは関係ありません(これがソースコードでどのように行われるかは記事の最後にあるリンクで確認できますが、これについては詳しく説明しません)。
次の構造に1つのグリッドノードを格納します。
struct Point{ float coord[2]; // 0 - x, 1 - y int index; };
ポイントの座標に加えて、2つの目的を持つノードのインデックスもあります。 まず、グリッドトポロジを復元するには、それだけで十分です。 次に、架空の要素を通常の要素と区別するために使用できます(たとえば、架空の要素の場合、このフィールドの値を-1に設定します)。 これらの架空の要素とは何か、なぜそれらが必要なのかについては、以下で詳しく説明します。
グリッド自体はPoint P [n1 * n2]配列に格納され、インデックス(i、j)を持つノードはP [i * n2 + j]に配置されます。 プログラムの結果として、ドメイン内の頂点の数は、値(n1 * n2 / k)を持つ1つの頂点に等しくなければなりません。
決定アルゴリズム
再帰的座標二分法の手順は、3つのステップで構成されます。
- 座標軸の1つに沿って(2次元の場合、xまたはyに沿って)ノードの配列をソートします。
- ソートされた配列を2つの部分に分割します。
- 受信したサブアレイのプロシージャの再帰的な開始。
ここでの再帰の基本は、k = 1の場合です(1つのドメインが残ります)。 このようなことが起こります:

または多分そう:
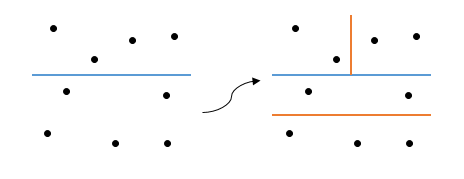
あいまいさはどこから来たのですか? 軸を選択するための基準を指定しなかったことは簡単にわかります。ここから、さまざまなオプションが表示されました(最初のステップでは、最初のケースでは、ソートはx軸に沿って、2番目ではy軸に沿って行われます)。 それでは、軸の選択方法は?
- ランダムに。
安くて陽気ですが、コードは1行だけで、最小限の時間で済みます。 デモプログラムでは、簡単にするために、同様の方法が使用されています(実際、各ステップで軸が反対に変わりますが、概念的な観点からは同じです)。 うまく書きたいのなら、そうしないでください。
- 幾何学的な理由から。
切開の長さは最小限に抑えられます(一般的な場合、切開は超平面であるため、多次元の場合、面積について話す方がより正確です)。 これを行うには、座標の最小値と最大値を持つポイントを選択し、メトリックに基づいて長さを測定します。 次に、取得した長さを比較し、適切な軸を選択するだけで十分です。 もちろん、反例を簡単に見つけることができます。

垂直セクションは短くなりますが、9つのエッジを横切りますが、長い水平セクションは4つのエッジのみを横切ります。 さらに、そのようなグリッドは縮退したケースではありませんが、問題に使用されます。 ただし、このオプションは、パーティションの速度と品質のバランスを表します。3番目のオプションほど多くの計算を必要としませんが、通常、パーティションの品質は最初の場合よりも優れています。
- カットリブの数を最小限にします。
スプリットエッジは、異なるドメインの頂点を接続するエッジです。 したがって、この数を最小化すると、ドメインは可能な限り「自律」として取得されるため、パーティションの高品質について話すことができます。 したがって、上の図では、このアルゴリズムは水平軸を選択します。 各軸に沿って配列を並べ替えてから、カットエッジの数を計算する必要があるため、高速で費用を支払う必要があります。
アレイを分割する方法に言及する価値があります。 m = n1 * n2 (ノードの総数と配列Pの長さ)、 kをドメインの数(以前と同様)とします。 次に、ドメインの数を半分に分割し、配列を同じ比率で分割しようとします。 数式の形式で:
int k1 = (k + 1) / 2; int k2 = k - k1; int m1 = m * (k1 / (double)k); int m2 = m - m1;
たとえば、9つの要素を3つのドメインに分割します( m = 9、k = 3 )。 次に、最初に配列が6対3の比率で分割され、次に6つの要素の配列が半分に分割されます。 その結果、それぞれに3つの要素を持つ3つのドメインを取得します。 必要なもの。
注:m1の式で実際の算術が必要な理由を尋ねる人がいるかもしれません。 たとえば、10000x10000のグリッドを100個のドメインm * k1 = 10 10に分割する場合、これはオーバーフローです。これはint範囲の境界を超えています。 注意してください!
シーケンシャルアルゴリズム
理論を理解したら、実装に進むことができます。 ソートには、標準C言語ライブラリのqsort()関数を使用します。 この関数は6つの引数を取ります:
void local_decompose(Point *a, int *domains, int domain_start, int k, int array_start, int n);
ここに:
- aは元のメッシュです。
- domains-グリッドノードのドメイン番号が格納される出力配列(配列aと同じ長さ)。
- domain_start-利用可能なドメイン番号の開始インデックス。
- kは使用可能なアイテムの数です。
- array_startは、配列の開始要素です。
- nは配列内の要素の数です。
最初に、再帰基底を記述します。
void local_decompose(Point *a, int *domains, int domain_start, int k, int array_start, int n) { if(k == 1){ for(int i = 0; i < n; i++) domains[array_start + i] = domain_start; return; }
ドメインが1つしか残っていない場合は、使用可能なすべてのグリッドノードをそこに配置します。 次に、軸を選択し、それに沿ってグリッドを並べ替えます。
axis = !axis; qsort(a + array_start, n, sizeof(Point), compare_points);
軸は、上記のいずれかの方法で選択できます。 この例では、前述のように、単に逆になります。 ここで、 軸は、 compare_points()要素比較関数で使用されるグローバル変数です。
int compare_points(const void *a, const void *b) { if(((Point*)a)->coord[axis] < ((Point*)b)->coord[axis]){ return -1; }else if(((Point*)a)->coord[axis] > ((Point*)b)->coord[axis]){ return 1; }else{ return 0 } }
次に、対応する式に従って、使用可能なドメインとグリッドノードを分類するだけです。
int k1 = (k + 1) / 2; int k2 = k - k1; int n1 = n * (k1 / (double)k); int n2 = n - n1;
そして、再帰呼び出しを書きます。
local_decompose(a, domains, domain_start, k1, array_start, n1); local_decompose(a, domains, domain_start + k1, k2, array_start + n1, n2); }
以上です。 local_decompose()関数の完全なソースコードは、githubで入手できます。
並列アルゴリズム
アルゴリズムが同じままであるという事実にもかかわらず、その並列実装ははるかに複雑です。 これは主に次の2つの理由によるものです。
1)システムは分散メモリを使用するため、各プロセッサはグリッド全体を見ることなくデータの一部のみを保存します。 このため、配列を分割するときは、要素を再配布する必要があります。
2)ソートアルゴリズムとして、並列Betcherソートが使用されます。これには、各プロセッサが同じ数の要素を持っている必要があります。
最初に、2番目の問題に対処しましょう。 解決策は簡単です-先に述べた架空の要素を導入する必要があります。 これは、 Point構造のインデックスフィールドが便利な場所です。 -1に等しくします-そして、私たちの前にダミー要素があります! すべてがうまくいくように見えますが、このソリューションでは、最初の問題を大幅に悪化させました。 一般的な場合、配列を2つの部分に分割する段階では、分割要素自体だけでなく、配列要素が配置されているプロセッサも判別できなくなります。 これを例で説明しましょう:4つのプロセッサで3つのドメインに分割する必要がある9つの要素(3x3グリッド)があるとします。 n = 9、k = 3、p =4。その後、ソート後、ダミー要素はどこにでも表示できます(図では、グリッドノードは緑、ダミー要素は赤)。

この場合、2番目の配列の最初の要素は2プロセッサーの中央にあります。 ただし、ダミー要素の配置が異なる場合、すべてが変更されます。

ここで、すでに壊れている要素は最後のプロセッサにありました。 このあいまいさを避けるために、小さなハックを使用します:ダミー要素の座標を可能な限り作成します(プログラムのfloat型の変数に格納されるため、値はFLT_MAXになります )。 結果として、ダミー要素は常に最後になります:

写真は、このアプローチでは、ダミー要素が最新のプロセッサに優先することを明確に示しています。 これらのプロセッサは無駄な作業を行い、再帰の各ステップでダミー要素をソートします。 ただし、現在、破壊要素の定義は簡単なタスクになり、プロセッサ上の次の番号になります。
int pc = n1 / elem_per_proc;
また、ローカル配列に次のインデックスがあります。
int middle = n1 % elem_per_proc;
破壊要素が決定されると、それを含むプロセッサは要素の再配布プロセスを開始します。すべての要素を破壊要素に「前に」(つまり、それより小さい数で)プロセッサに均等に配布し、必要に応じてダミー要素を追加します。 彼は送信された要素をダミーのものに置き換えます。 n = 15、k = 5、p = 4の写真では:
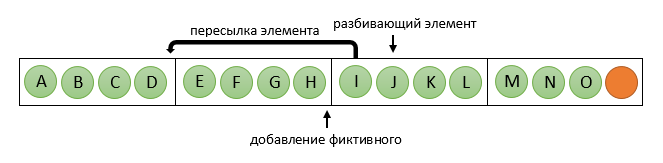

これで、 pcより小さい数のプロセッサーは、元のアレイの最初の部分で引き続き動作し、残りの部分は2番目の部分で並行して動作します。 同時に、1つのグループのフレームワーク内で、すべてのプロセッサの要素の数は同じです(ただし、2番目のグループは異なる要素を持つ場合があります)。これにより、Betcherソートをさらに使用できます。 ケースpc = 0が可能であることを忘れないでください-その後、「反対側」に要素を送信するだけで十分です。 多数のプロセッサに。
並列アルゴリズムの再帰基底は、まずプロセッサを使い果たしたときに考慮する必要があります。k= 1の場合は残りますが、実際にはドメインの数は通常プロセッサの数より多いため、縮退しています。
上記に基づいて、関数の一般的なスキームは次のようになります。
分解機能の概要
void decompose(Point **array, int **domains, int domain_start, int k, int n, int *elem_per_proc, MPI_Comm communicator) { // int rank, proc_count; MPI_Comm_rank(communicator, &rank); MPI_Comm_size(communicator, &proc_count); // if(proc_count == 1){ // , local_decompose(...); return; } if(k == 1){ // , return; } // 2 int k1 = (k + 1) / 2; int k2 = k - k1; int n1 = n * (k1 / (double)k); int n2 = n - n1; // int pc = n1 / (*elem_per_proc); int middle = n1 % (*elem_per_proc); // 2 , // int color; if(pc == 0) color = rank > pc ? 0 : 1; else color = rank >= pc ? 0 : 1; MPI_Comm new_comm; MPI_Comm_split(communicator, color, rank, &new_comm); // axis = ... sort_array(*array, *elem_per_proc, communicator); if(pc == 0){ // // return; } // // if(rank < pc) decompose(array, domains, domain_start, k1, n1, elem_per_proc, new_comm); else decompose(array, domains, domain_start + k1, k2, n2, elem_per_proc, new_comm); }
おわりに
アルゴリズムの実装にはいくつかの欠点がありますが、同時に否定できない利点もあります。 プログラムのソースコードはgithubにあります。 結果を表示するための補助ユーティリティもあります。 この記事の準備では、M。V. Yakobovsky著の「問題を解決するための並列メソッドの紹介」の資料を使用しました。