👈🏼 👨🏾‍🏫 👧🏾 株式市場における定常的な増加を伴う非定常プロセスのクラスの分析 💤 👳 🤳🏿

この記事の目的は、Dickey-Fullerテストを使用して定常性を確認することにより、モスクワ取引所とNYSEで取引される株価の値の構造を特定する調査結果を共有することです。

在庫の小さなクラスがあります。これは、静止増分とt統計の分布を伴う非定常プロセスであり、かなり奇妙な方法で動作します。つまり、観測数の増加に伴う標準正規分布の傾向はありません。そのような共有を識別する方法は？

データ収集

最初に必要なのは、ブローカーの1つを介して実際に取引できるティッカーのリストです。ティッカーは、クォートされた銘柄（この場合は株式）の交換情報における短い名前です。ロシアの株式市場から始めます。最も人気のある取引所-モスクワがあるので、それについて話しましょう。

人生のある時点で、オフラインになり、Sberbankと仲介サービス契約を締結しました。この状況では、ティッカーのリストは非常に簡単に取得できます。 QUIKシステムをダウンロードし、株式の株価情報フローを注文するだけで十分です。

次に、[取引]タブにそれらを表示し、テーブルをファイルに保存します。合計296ティッカー。自分でクエストを手配したくない場合は、モスクワ取引所のウェブサイトのデータ例セクションにティッカーのリストがあります。唯一のものは、おそらくこのリストは古くなっています。

次に必要なのは株価データです。それらのどれだけが市場の適切な状況を描くために必要であり、どの期間それらを採用するかは議論の問題です。さらに発生する技術的な制限は、各銘柄につき最低10個の値です。

以前に受け取ったティッカーから2016年（252取引日）の終値のデータを取得したかったのですが、より短い期間のデータを取得でき、日中の調査もできます。概して、どのデータを取得するかは今ではそれほど重要ではありません。唯一のものは、モスクワ証券取引所に行き、2016年のアーカイブデータを彼女に尋ねると、彼女は32,400ルーブルをすべてのものに支払わなければならないことを教えてくれます（以前は、データコストがさらにかかります）。危害からパーサーを作成しました。

実際、決勝戦やYahoo Financeからデータを取得する方がはるかに高速ですが、何らかの理由でそれほど面白くありません。かつて、私は情報監査グループのトップに連絡して、研究のためにサイトを解析できるかどうかを尋ねました。許された。

[パーサーに関する文字とコードがたくさんありましたが、おそらくあまり面白くないのですべてを削除しました。間違えたら、パーサーを別の記事として公開します。]

私は289株のデータを収集しました（残りのデータはありませんでした）。便宜上、ティッカーと価格はMicrosoft SQL Serverデータベースに保存されていました。数学に移りましょう。

定常性について

公式や複雑な概念のない定常性について話す場合、ポイントは、定常系列が期待値、分散、共分散などの特性を経時的に変化させないことです。

株価は、1のオーダーの自己回帰プロセスと見なすことができます。

$y_ {t} = \ phi y_ {t-1} + \ varepsilon_ {t}、$

どこで $\ピ$ -モデルパラメーター、 $\ varepsilon_ {t} \ sim iid（0、\ sigma ^ 2）$ -ホワイトノイズ t = 1、...、n

。このようなプロセスは固定的です $| \ phi |＆lt; 1$ 。

252取引日の株価があるとします。そのような自己回帰プロセスが定常であるかどうかは、利用可能な観測からどのように判断できますか？標準的な仮説検定手順を実施する必要があります H_0

： $\ phi = 1$ （つまり、プロセスは定常的ではない）対対立仮説 H_1

： $\ファイ＆lt; 1$ （つまり、プロセスは静止しています）。

Dickey-Fullerディストリビューションについて

実際、仮説のテストはそれほど単純ではありません。 $\ phi = 1$ 、t統計量はスチューデントの法則に従って分布せず、その分布は観測数の増加に伴い標準正規になる傾向はありません。この場合、学生の重要な値の表を取得して、それに対して仮説をテストすることはできません。

ここで、t統計は、自己回帰モデルのパラメーター推定値の真値からの偏差と係数推定値の標準誤差との比として理解されます。

$t = \ frac {\ hat {\ phi}-\ phi} {s _ {\ hat {\ phi}}}、$

どこで $\ hat {\ phi}$ -自己回帰モデルのパラメーターの推定（1）、 $s _ {\ hat {\ phi}}$ -標準推定誤差 $\ hat {\ phi}$ 。係数推定 $\ hat {\ phi}$ 代替モデルでは、従来の最小二乗法（OLS）を使用して実行できます。

ウェインフラーは1976年に、t統計が大丈夫ではないことを初めて話し始めました。その後、1979年に、David Dickeyと共同で、「単位根をもつ自己回帰時系列の推定量の分布」という興味深い記事を執筆しました。

冷静な頭でそれを解析することはほとんど不可能ですが、提供されたt統計の分布を提示したのはそこにありました $\ phi = 1$ 、つまり $t = \ frac {\ hat {\ phi}-1} {s _ {\ hat {\ phi}}}$ （これはDickey-Fuller統計と呼ばれます）、式（1）とその2つの修正について：

$y_ {t} = a + \ phi y_ {t-1} + \ varepsilon_ {t}、$

$y_ {t} = a + \ phi y_ {t-1} + ct + \ varepsilon_ {t}。$

方程式（1）の場合、Dickey-Fuller分布の形式は次のとおりです。

$\ lim t_1 = \ frac {W ^ 2（1）-1} {2 \ sqrt {\ int_ {0} ^ {1} W ^ 2（s）ds}}、$

どこで

-プロセスのt統計（1）、 W（秒）

-標準Wienerプロセス。

Dickey-Fuller統計の重要な値は、Fullerの著書「Introduction to Statistical Time Series」に記載されています。したがって、定常性の自己回帰プロセスを確認するには、スチューデント分布の臨界値テーブルの代わりに、ディッキーフラー分布の臨界値テーブルを使用する必要があるという違いを伴う標準の仮説検定手順を使用する必要があります。

方程式（1）、（2）、および（3）は次の形式で書き換えることができることに注意することも重要です。

$y_ {t}-y_ {t-1} = \ phi y_ {t-1}-y_ {t-1} + \ varepsilon_ {t}、$

$\デルタy_ {t} =（\ phi-1）y_ {t-1} + \ varepsilon_ {t}、$

$\デルタy_ {t} = \ beta y_ {t-1} + \ varepsilon_ {t}、$

$y_ {t}-y_ {t-1} = a + \ phi y_ {t-1}-y_ {t-1} + \ varepsilon_ {t}、$

$\デルタy_ {t} = a +（\ phi-1）y_ {t-1} + \ varepsilon_ {t}、$

$\デルタy_ {t} = a + \ beta y_ {t-1} + \ varepsilon_ {t}、$

$y_ {t}-y_ {t-1} = a + \ phi y_ {t-1}-y_ {t-1} + ct + \ varepsilon_ {t}、$

$\デルタy_ {t} = a +（\ phi-1）y_ {t-1} + ct + \ varepsilon_ {t}、$

$\ Delta y_ {t} = a + \ beta y_ {t-1} + ct + \ varepsilon_ {t}、$

どこで $\デルタy_ {t} = y_ {t}-y_ {t-1}$ 、そして $\ベータ= \ファイ-1$ 。プロセス（4）、（5）および（6）は、 $\ベータ= 0$ 仮説をテストすることに似ています $\ phi = 1$ 。したがって、Dickey-Fuller統計により、プロセス自体の定常性だけでなく、その1次差分の定常性も検証できます。

Dickey-Fullerテストについて

Dickey-Fullerテストはすべての標準パッケージで利用できるため、MATLABなどでデータ収集段階で取得した株価の定常性を確認できます。以下は、Microsoft SQL Serverデータベース（株価とティッカーが格納されている）への接続を確立し、2つの配列が作成されるコードです。 1つ目は価格の直接値、2つ目は価格データのあるティッカーのみの値です。

conn = database.ODBCConnection('uXXXXXX.mssql.masterhost.ru', 'uXXXXXX', 'XXXXXXXXXX'); curs = exec(conn, 'SELECT ALL PriceId, StockId, Date, Price FROM StockPrices'); curs = fetch(curs); data = curs.Data idsArr = unique(cell2mat(data(:,2))); sqlquery = 'SELECT ALL StockId, ShortName, Code FROM Stocks WHERE StockId IN ('; for i=1:length(idsArr) if i==length(idsArr) sqlquery = strcat(sqlquery,int2str(idsArr(i)),')'); else sqlquery = strcat(sqlquery,int2str(idsArr(i)),','); end end curs = exec(conn, sqlquery); curs = fetch(curs); names = curs.Data close(conn);

Dickey-Fullerテストはadftest関数を使用して実行されます。この関数は、入力で1次元の時系列を取得し、帰無仮説が棄却された場合は論理値1を返し、そうでない場合は0を返します。フォーム（1）のモデルに対して5％の有意水準でDickey-Fuller検定を実行してみましょう。

 for i = 1:length(names) % Indexes with current stock's data indexes = find(cell2mat(data(:,2)) == cell2mat(names(i,1))); isStat(i) = adftest(cell2mat(data(indexes,4))); end % Indexes with stationary stocks stat = find(isStat == 1);

プログラムは、代替モデルを支持して帰無仮説を5回拒否します。これらの時系列を示します：

 for i=1:length(stat) indexes = find(cell2mat(data(:,2)) == cell2mat(names(stat(i),1))); figure plot(datetime(data(indexes,3)), cell2mat(data(indexes,4))) legend(names(stat(i),3)); end

株式の価格チャートを見てみましょう。

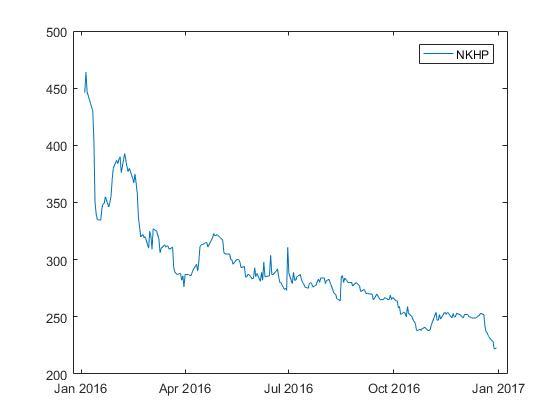
ここでは、株価の時系列が定常的ではないことがわかります。

与えられた時系列の1次差分を構築します。

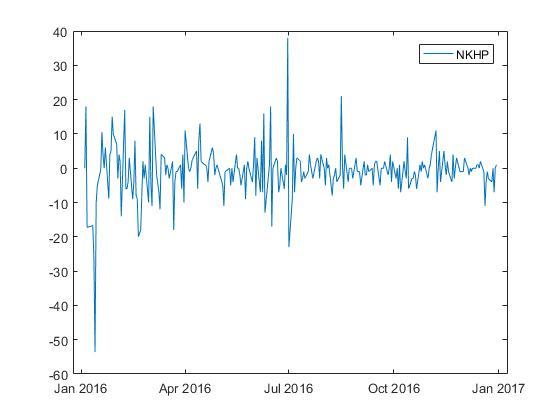
株価の時系列の最初の注文の差は、定常条件を本当に満たしているようです。

NYSEの結果

同じ研究が米国の株式市場、つまりニューヨーク証券取引所で実施されました。ティッカーのリストは、 NASDAQ Webサイトから取得されました。現在、2,714の適切なティッカーがあります。価格データはYahoo Financeから取得しました。 2016年の株価に関するデータがある2647ティッカーがあり、定常性のテストの結果、固定増分の26銘柄が取得されました。

結論

株式市場には多数の資産があり、価格の変化は定常的な増加を伴う非定常的なプロセスです。このようなプロセスの存在は、さらなる研究と安定した利益創出の基礎となりますが、次回はこのことについてお話します。

トピックについて何を読むべきですか？

マグナス、Y.R。計量経済学。初心者コース/ Ya.R. マグナス、P.K。カティシェフ、AA ペレセツキー。 -M。：ビジネス、2004 .-- 576 p。

これは計量経済学に関する非常に優れた教科書であり、ブルジョアよりも悪くはありません。また、普通に書かれているので、理解することができます。

UPD。モスクワ証券取引所における2017年の固定増分在庫分析。

株式市場における定常的な増加を伴う非定常プロセスのクラスの分析