Clever Geek Handbook

ハトは人間よりも優れたモンティ・ホールの逆説

ハトは人々にモンティホールのジレンマを解決するための有利なスタートを与えます。 このパターンは、なぜ人々がそれを与えるのがそれほど難しいのかを明らかにすることができます。













このジレンマで注目すべき点は何ですか？ シンプルに見えるが、それは私たちの結論の論理的連鎖を混乱させ、人々（文字ではなく、ハト）を文字通り、3本の松、またはむしろドアをさまようことを強いる。 これは、さまざまな文化的伝統の代表者にとって典型的なものです。アメリカ人、中国人、スウェーデン人、ブラジル人は同じ間違った選択をします。







認知心理学者のマッシモ・ピアテッリ・パルマリーニはこの主題について次のように述べています。







この記事では、ジレンマの構成要素を見つけ、理論的に正しい解決策を見つけ、Rでそれを確認し、ハトを持つ人々の知的戦いについて話し、その結果を見つけます。







モンティホールジレンマ



いわゆるモンティホールのジレンマは有名なミステリーであり、アメリカのテレビ番組「I Offer a Deal」の最初のテレビプレゼンターにちなんで名付けられました。 賞品とヤギはランダムに事前に配置された後、場所を変更しませんでした。 参加者が選択した後、ホストは常に残りの2つのドアの1つを開けました。 それから、プレーヤーは彼らの選択を変えるか、またはすべてをそのままにする機会を提供されました 。













実際には、 いくつかの可能なMonty戦略があります。









リーダーの公平性戦略は、最初のプレイヤーの選択でヤギのドアを開き、 選択を変更するか、すべてをそのままにすることを提案するときに古典になりました。 それから、私たちは構築を続けます。







プレイヤー、回答者、および被験者の大多数は、勝つチャンスが2倍になったにもかかわらず、 選択の変更を拒否しました。 同時に、人々は残りの2つのドアで勝つ可能性は等しく、選択を変える意味はないと考えています。 あなたが同じだと思うなら、恥ずかしがらないでください。あなたが間違っているのはあなただけではないからです。







コラムニストMarilin vos Savant [1]がパレードマガジンでこの決定を発表したとき、 読者からの不一致を表明する手紙が急増しました。 以下に例を示します。







すぐに、高等学校や大学の生徒から多くの手紙が届くと思います。 おそらくこれらのアドレスを保持する必要があります。将来のリリースで役立ちます。

W.ロバートスミス博士 /ジョージア州立大学



少なくとも3人の数学者があなたを訂正した後でも、あなたはまだあなたの間違いを見ないことにショックを受けました。

ケントフォード/ディキンソン州立大学



あなたはヤギです。

グレンカルキンズ/ウェスタンステートカレッジ

合計で-約1万文字。 ご覧のように、トローリングは、今よりもはるかに多くの時間と労力を費やし、郵便封筒と切手にお金を払う必要があった当時でさえ盛んに行われました。







才能のあるハンガリーの数学者ポール・エルデスもまた、このトリックにforれ、実験結果のコンピューターシミュレーションを自分の目で見るまで、決断を下すことさえ拒否しました。 正直なところ、私はそれをほとんど信じていませんが、それでも噂は行きました。







ばく露



DMX（Monty Hall Dilemma）ソリューションの最も簡潔な説明は、円グラフで提供されます。













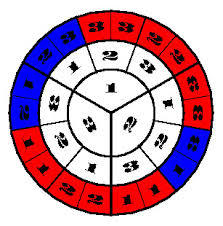
, — , . — . , 1/3



, 2/3



.







, .















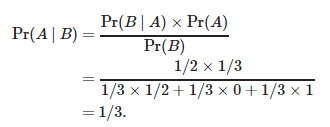
Pr(A)



— 3 , 1/3



. , Pr(B|A)=1/2



.

Pr(B)



, , . , :







  1. 1, 2.
  2. 1- , 1/2 2.
  3. 2- , 3, .
  4. 3- , 2, .


, 1/3, . , , , 2/3.







?



, Julia Schroder Walter Hebranson , - .







. , , — .







. . , , . , , - . — , . . .







30 36.33% 96.33%.













: — . — . — .







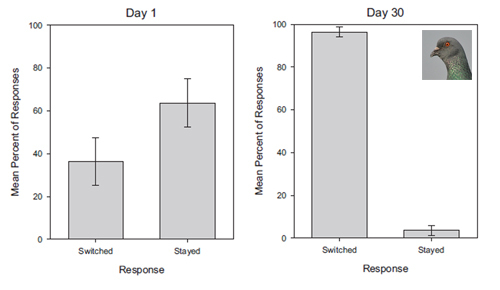
. 30 , .













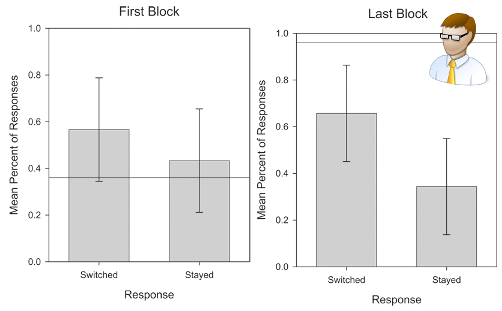
56.67% 65.67%. , .







, , . . , .







. . 30.17% , 15- — 4.33%. home sapiens : 30%, — 27.67%.







?



. , . . . . , , , .







: , , . , .







. , , , R. .







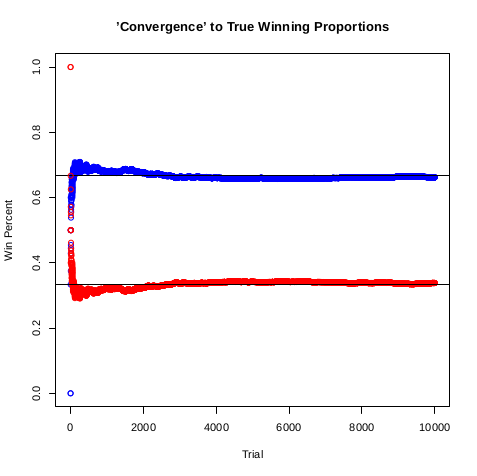
5:543)$ R -f monty.r

 Monty Hall Problem Simulation
"  "

                            = 3380 
                 = 10000 
       = 0.338 
      = 0.3333333 

" "

                            = 6620 
                 = 10000 
       = 0.662 
     = 0.6666667> 
> ## Plot 'convergence' to true winning proportions
> ## Blue is switching doors, red is staying
> plot.new()
> plot(cumsum(changewin) / c(1:N), main = "'Convergence' to True Winning Proportions",
+      xlab = "Trial", ylab = "Win Percent", ylim = c(0, 1), col = "blue")
> abline(h = 2/3)
> points(cumsum(staywin) / c(1:N), type = "p", col = "red")
> abline(h = 1/3)


1/3



2/3



.















  1. Are Birds Smarter Than Mathematicians? Pigeons (Columba livia) Perform Optimally on a Version of the Monty Hall Dilemma
  2. Pigeons Beat Humans at Solving 'Monty Hall' Problem
  3. Pigeons outperform humans at the Monty Hall Dilemma
  4. Monty Hall Problem: Intuitive and Mathematical Solutions




  1. ↑ Ask Merilin, IQ.


More articles:


All Articles