Clever Geek Handbook

JavaScriptでキャンバスに任意の角度で楕円を描く

1つのアプリケーションを開発する過程で、JavaScriptのキャンバスに任意の角度で楕円を描画する必要に直面しました。 このような単純なプロジェクトではフレームワークを使いたくなかったので、このトピックに関するマニュアル記事を探しました。 検索が失敗したため、私は自分でタスクを処理する必要があり、私はあなたと得た経験を共有することにしました。



問題を形式化します。 drawEllipse関数（coords、sizes、vector）が必要です。ここで：





この記事では、この問題を解決する3つの方法を提供します。





最初の方法としてベジェ曲線が選択されました。 このような曲線を作成するには、開始点、終了点、2つの制御点の4つの点が必要です。







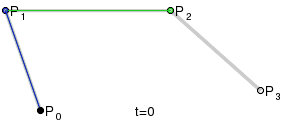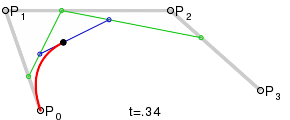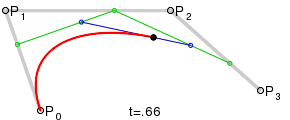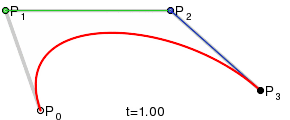
目的の楕円は、このような2つの曲線で構成され、それぞれの上記の点が長方形の頂点になると推測するのは簡単です。 楕円を見てみましょう。







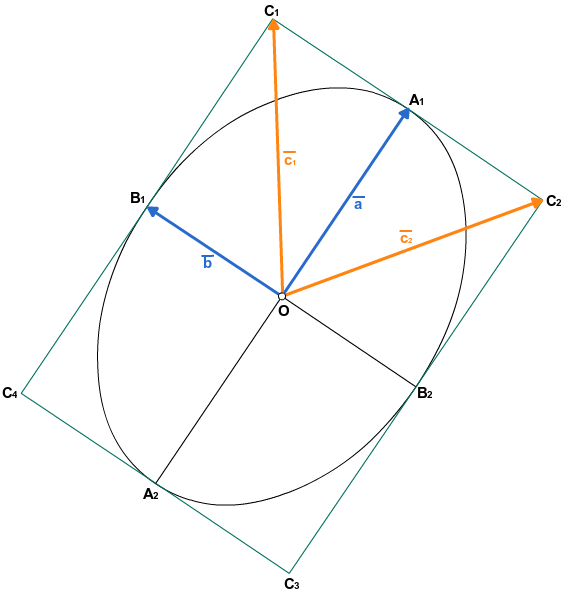
  1. ベクトルがあります

    単位ベクトルを見つける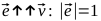





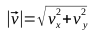
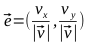
    単位ベクトルを見つける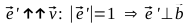

    これを行うには、ベクトルのスカラー積のプロパティを思い出してください。これらのベクトルが垂直の場合は消えます。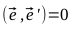

    このように：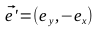
  2. ベクトルを見つける 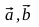、ポイントA 1 、A 2 、B 1 、B 2











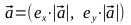
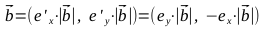
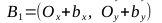
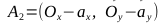
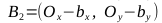
  3. ベクトルを見つける 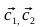、ポイントC 1 、C 2 、C 3 、C 4











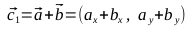
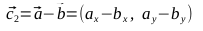
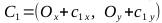
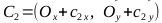
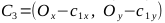
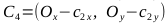
  4. 楕円を描くには、2つのベジェ曲線が必要であることを思い出してください。

    • 1stには開始点B 1があり 、終了点B 2が点A 1を通過します
    • 2番目には開始点B 2 、終了点B 1があり、点A 2を通過します
    ベジェ曲線を作成するには、制御点が必要であることも思い出してください。 考え直すことなく、まず楕円が内接する長方形の頂点を置き換えました。 この解決策は間違いであることが判明しました。ベジェ曲線の作成を検討すると、2つの制御点を接続するセグメントに触れないことがわかります。

    ベジエ曲線（曲線）が制御点間のセグメントに最も近くなる点でのベジエ曲線の構築の瞬間を示してみましょう。 この場合、次のようになります。







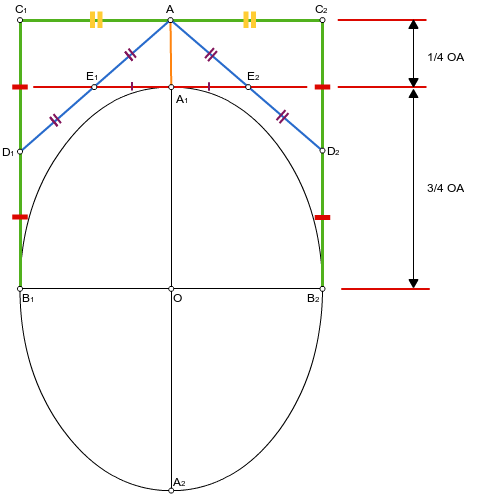
    図から、この点（A 1 ）から制御点（C 1 、C 2 ）間のセグメントまでの距離は、目的の楕円（O）の中心と同じセグメント（C 1 、C 2 ）間の距離の1/4になることが明らかです。あります：



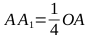
  5. xでOAを表します。 方程式を解く





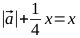
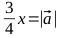
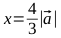
    したがって、必要なパラメーターで楕円を取得するには、ベクトルを乗算する必要があります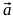 パラメーターごと 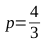その後、パラグラフ1〜4で説明した計算に戻ります。 その結果、目的の形状を一緒に表す2つのベジェ曲線を作成するためのポイントのセット（ B 1 、C 1 、C 2 、B 2およびB 2 、C 3 、C 4 、B 1 ）を取得します。





実際にデモとコード： 



function drawEllipse(ctx, coords, sizes, vector) { var vLen = Math.sqrt(vector[0]*vector[0]+vector[1]*vector[1]); //    var e = [vector[0]/vLen, vector[1]/vLen]; //   e || vector var p = 4/3; //  var a = [e[0]*sizes[0]*p, e[1]*sizes[0]*p]; //   a,   var b = [e[1]*sizes[1], -e[0]*sizes[1]]; //   b //   A1, B1, A2, B2 var dotA1 = [coords[0]+a[0], coords[1]+a[1]]; var dotB1 = [coords[0]+b[0], coords[1]+b[1]]; var dotA2 = [coords[0]-a[0], coords[1]-a[1]]; var dotB2 = [coords[0]-b[0], coords[1]-b[1]]; //   c1, c2 var c1 = [a[0]+b[0], a[1]+b[1]]; var c2 = [a[0]-b[0], a[1]-b[1]]; //   C1, C2, C3, C4 var dotC1 = [coords[0]+c1[0], coords[1]+c1[1]]; var dotC2 = [coords[0]+c2[0], coords[1]+c2[1]]; var dotC3 = [coords[0]-c1[0], coords[1]-c1[1]]; var dotC4 = [coords[0]-c2[0], coords[1]-c2[1]]; //    ctx.strokeStyle = 'black'; ctx.beginPath(); ctx.moveTo(dotB1[0], dotB1[1]); //   ctx.bezierCurveTo(dotC1[0], dotC1[1], dotC2[0], dotC2[1], dotB2[0], dotB2[1]); //    ctx.bezierCurveTo(dotC3[0], dotC3[1], dotC4[0], dotC4[1], dotB1[0], dotB1[1]); //    ,     ctx.stroke(); ctx.closePath(); //   a   a = [e[0]*sizes[0], e[1]*sizes[0]]; //       ,  ,       ctx.beginPath(); ctx.moveTo(coords[0]+a[0], coords[1]+a[1]); ctx.lineTo(coords[0]-a[0], coords[1]-a[1]); ctx.moveTo(coords[0]+b[0], coords[1]+b[1]); ctx.lineTo(coords[0]-b[0], coords[1]-b[1]); ctx.strokeStyle = 'red'; ctx.stroke(); ctx.closePath(); }




更新しました。 コメントを確認した後、パラメトリック方程式を使用して楕円を描画する機能を作成しましたが、ベジェ曲線を使用して取得した図形が楕円と正確に一致しないことがわかりました。 図形のオーバーレイでは、ベジェ曲線によって描かれたオブジェクト（赤）が通常の楕円（青）よりも広いことがあります。 これは、重なり合う形状のデモです 。 
 function drawEllipseParam(ctx, coords, sizes, angle, segments) { ctx.save(); ctx.translate(coords[0], coords[1]); ctx.rotate(angle); ctx.beginPath(); var x, y, firstTime=true; var dt = 2*Math.PI/segments; for(var t=0; t<2*Math.PI; t+=dt) { x = sizes[0]*Math.cos(t); y = sizes[1]*Math.sin(t); if(firstTime) { firstTime = false; ctx.moveTo(x, y); } else { ctx.lineTo(x, y); } } ctx.strokeStyle = 'blue'; ctx.stroke(); ctx.closePath(); ctx.restore(); }




更新しました。 コメントは、斜めの楕円を描くためのよりネイティブでシンプルな方法を提案しました（ subzeyに感謝）。 迷子にならないようにここを離れます。 これがデモです。 



 function drawEllipse(ctx, coords, sizes, angle) { ctx.beginPath(); ctx.save(); //    ctx.translate(coords[0], coords[1]); //      ctx.rotate(angle); //       ctx.scale(1, sizes[1]/sizes[0]); //    ctx.arc(0, 0, sizes[0], 0, Math.PI*2); //   ctx.restore(); //  ,         ctx.strokeStyle = 'green'; ctx.stroke(); //  ctx.closePath(); }


More articles:


All Articles