 こんにちは、Habr、長い間お互いに会いませんでした。 この投稿では、機械学習における転移学習などの比較的新しい概念についてお話したいと思います。 私はこの用語の確立された翻訳を見つけられなかったので、投稿のタイトルには異なるが類似した用語も含まれています。これは、あるモデルから別のモデルへの知識伝達の理論を形式化するための生物学的前提条件のようです。 したがって、計画は次のとおりです。最初に、生物学的背景を考慮します。 ディープニューラルネットワークの事前トレーニングという非常に類似したアイデアからの転移学習の違いに触れた後、 最後に、セマンティックイメージハッシュの実際の問題について説明します。 これを行うために、「ローカリゼーションと分類」セクション(オックスフォード大学のVisual Geometry Group )でimagenet 2014コンテストの勝者の深い(19層)畳み込みニューラルネットワークを取得し、少し工夫して、いくつかの層を抽出し、それらを使用します目的。 行こう
こんにちは、Habr、長い間お互いに会いませんでした。 この投稿では、機械学習における転移学習などの比較的新しい概念についてお話したいと思います。 私はこの用語の確立された翻訳を見つけられなかったので、投稿のタイトルには異なるが類似した用語も含まれています。これは、あるモデルから別のモデルへの知識伝達の理論を形式化するための生物学的前提条件のようです。 したがって、計画は次のとおりです。最初に、生物学的背景を考慮します。 ディープニューラルネットワークの事前トレーニングという非常に類似したアイデアからの転移学習の違いに触れた後、 最後に、セマンティックイメージハッシュの実際の問題について説明します。 これを行うために、「ローカリゼーションと分類」セクション(オックスフォード大学のVisual Geometry Group )でimagenet 2014コンテストの勝者の深い(19層)畳み込みニューラルネットワークを取得し、少し工夫して、いくつかの層を抽出し、それらを使用します目的。 行こう
神経可塑性
まず、定義を検討します。 神経可塑性は、経験の影響下または損傷後に変化する脳の特性です。 変更には、 シナプス接続の作成と新しいニューロンの作成の両方が含まれます。 比較的最近まで、20世紀の70年代まで、脳の一部、特に新皮質 (これは、すべての運動能力、言語、思考など)が、一定の成長期間後に静止したままであり、調整しかできないと考えられていましたニューロン間の接続の強さ。 しかし、後により詳細な研究により、脳全体の神経可塑性の存在が確認されました。 短いビデオをご覧になることをお勧めします。
私たちの脳の力を本当に感じるために、神経生理学者のポール・バッハ・リタの実験を見てみましょう。彼の研究は科学界による神経可塑性の認識に大きな影響を与えました。 科学者の動機に影響を与える重要な要因は、父親が麻痺したという事実でした。 兄弟の物理学者と一緒に、彼らは68歳までに父親を立ち上げることができたので、彼は極端なスポーツに従事することさえできました。 彼らの歴史は、後年になっても人間の脳はリハビリテーションが可能であることを示しています。 しかし、これは1969年の経験に完全に異なる話です。 目標は深刻でした。視覚障害者(出生時から)に見る機会を与えることです。 これを行うために、歯科用椅子を取り、次のように再取り付けしました。椅子の隣にテレビカメラを置き、マニピュレーターを椅子に持ってきて、カメラのスケールと位置を変更できるようにしました。 400の刺激装置が椅子の後ろに取り付けられ、グリッドを形成しました。カメラから受信した画像は20 x 20のサイズに圧縮されました。 覚醒剤は、互いに12 mmの距離に配置されました。 小さな刺激装置が各刺激装置に取り付けられ、刺激装置の内部にあるソレノイドに供給される電流に比例して振動しました。

オシロスコープを使用して、覚醒剤の振動によって作成された画像を視覚化することができました。

1年後、ポールは自分のシステムのモバイルバージョンを開発しました。
1970年代のモバイルバイザー
男はマヴロディに似ていますが、それは彼ではありません。


最近では、触覚信号伝達の代わりに、より敏感な器官である「言語」を通る「短い」経路を使用します。 彼らが記事で言うように、数時間は言語の受容者によってイメージを知覚し始めるのに十分です。
現代のオプション
それでは、どのように機能しますか? 単純な言語(生物学者や神経生理学者ではなく、データ分析の言語)で話すことで、ニューロンは標識を効率的に抽出して結論を引き出すように訓練されます。 おなじみの信号を他の信号に置き換えると、ニューラルネットワークは、センサーに近いレイヤー(目、舌、耳など)で優れた低レベルの特徴を抽出します(以下に示すコンピュータービジョンを使用すると、これらはさまざまなグラデーション遷移またはパターンになります) d。)。 より深い層は、より高いレベルの属性(ホイール、ウィンドウ)を抽出しようとします。 そしておそらく、音声信号で車のホイールを探しても、おそらく見つけられないでしょう。 残念ながら、ニューロンが抽出する兆候を確認することはできませんが、記事「 畳み込みネットワークの視覚化と理解 」のおかげで、深い畳み込みニューラルネットワークによって抽出された低レベルおよび高レベルの特徴を見る機会があります。 もちろん、これは生物学的ネットワークではなく、おそらく現実のすべてがそうではありません。 少なくとも、これは言語受容体を見ることができる理由のある種の直感的な理解を提供します。
スポイラーの大きな画像は、各畳み込み層のいくつかの特徴と、それらを活性化する元の画像の一部を示しています。 ご覧のように、深くなるほど、記号は抽象的ではなくなります。
完全に訓練されたモデルの特徴の可視化
灰色の各正方形は、フィルター(畳み込みに使用)または1つのニューロンの重みの視覚化に対応し、各カラー画像は、対応するニューロンをアクティブにする元の画像の部分です。 わかりやすくするために、1つのレイヤー内のニューロンはテーマグループにグループ化されています。


センサーを交換すると、脳はすべてのニューロンを完全に再トレーニングする必要はなく、高レベルの特徴を抽出するニューロンのみを再トレーニングするだけで十分であり、残りはすでに高品質の特徴を抽出できると想定できます。 実践では、ほぼ同じであることが示されています。 舌の上にプレートを置いて数時間歩くと、舌の受容体で食べ物の味を感じる能力を失うことなく、脳が新しいシナプス結合を除去して成長させることはほとんどありません。
そして、人工ニューラルネットワークの歴史がどのように始まったかを思い出しましょう。 1949年、ドナルドヘブは、 行動の組織という本を出版しました。 最新の学習アルゴリズムがこれらの原則からそれほど遠くないことは注目に値します。
- 隣接するニューロンが同期的に活性化されると、それらの間の接続が強化されます。
- 隣接するニューロンが非同期にアクティブ化されると、それらの間の接続が弱まります (実際、ヘブにはこのルールがなく、追加として後で追加されました)。
9年後、 フランクローゼンブラットは教師と一緒に教える最初のモデル、 パーセプトロンを作成しました 。 最初の人工ニューラルネットワークの作成者は、普遍的な近似器を作成するという目標を追求しませんでした。 彼は神経生理学者であり、彼の仕事は人間のように訓練できるデバイスを作成することでした。 ジャーナリストがパーセプトロンについて書いているものを見てください。 私見、これは素敵です:
ニューヨークタイム、1958年7月8日 
...


...

パーセプトロンでは、ヘブの学習ルールが実装されました。 ご覧のとおり、ルールのシナプス可塑性はすでにある程度考慮されています。 そして、原則として、 オンライン学習はある程度の可塑性を与えます-ニューラルネットワークは継続的なデータストリームで絶えず再訓練でき、これに関連する予測は、データの変化を常に考慮して、時間とともに変化します。 しかし、感覚置換や神経新生など、神経可塑性の他の側面に関する推奨事項はありません。 しかし、これは驚くべきことではありません。神経可塑性が採用されるまで、わずか20年以上が残ります。 ANNのその後の歴史を考えると、科学者たちは神経可塑性をシミュレートすることはできませんでしたが、問題は原理の理論の存続についてでした。 2000年代のニューラルネットワークの次のルネッサンスの後、他の科学者は、 ヒントン 、 ルクン 、 ベンジオ 、 シュミット チューバーなどの人々のおかげで、機械学習に包括的にアプローチし、転移学習の概念に到達する機会を得ました。
転移学習
転移学習の目標を定義します。 同じ名前の 2009年の出版物の著者は、3つの主な目標を特定しています。
- より高い開始-モデルの初期パラメーターまたはその他の事前情報のより徹底的な選択により、初期反復で既にトレーニングの品質を向上させます。
- より高い勾配-学習アルゴリズムの収束の加速;
- より高い漸近線-達成可能な上限品質の改善。
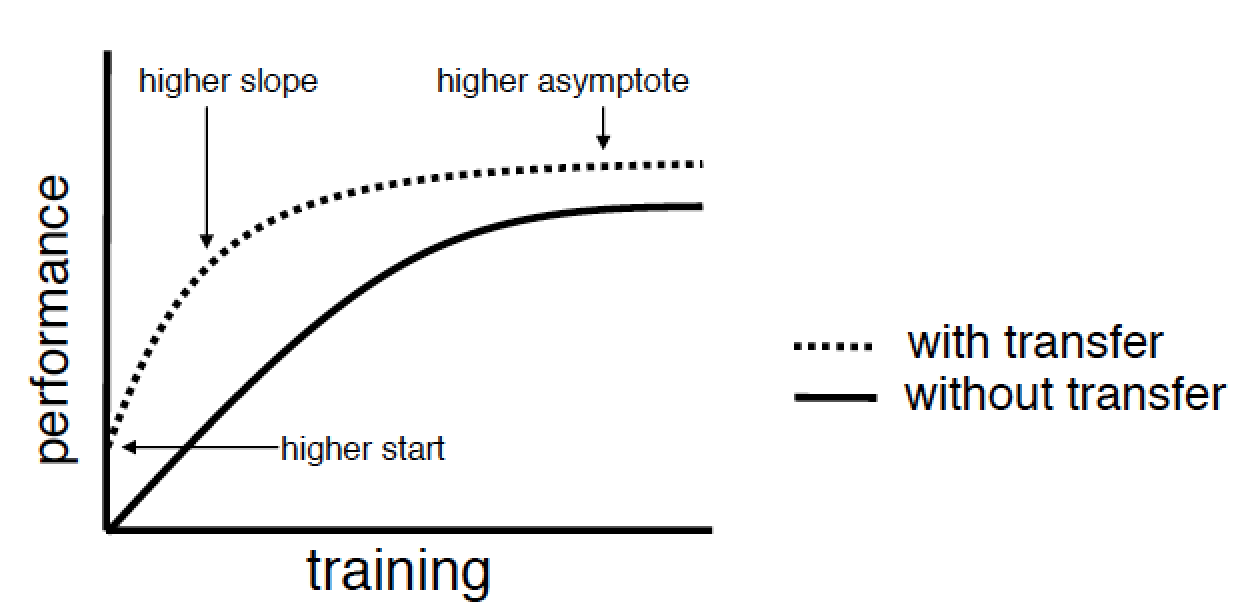
オートエンコーダーまたは限定的なボルツマンマシンを使用した詳細なネットワーク事前トレーニングに精通している場合、すぐに次のように思うでしょう。「それで、私はすでに転移学習を実践しているか、少なくとも、それを行う方法を知っています。」 しかし、そうではありません。 著者は、標準的な機械学習と転移学習の間に明確な線を引きます。 標準的なアプローチでは、目標とデータセットのみがあり、タスクは任意の方法でこの目標を達成することです。 問題の解決策の一部として、深いネットワークを構築し、貪欲なアルゴリズムで事前に訓練し、さらに数十個を構築し、何らかの方法でそれらのアンサンブルを作成できます。 しかし、これはすべて単一の問題を解決するフレームワーク内にあり、そのような問題の解決に費やされる時間は、各モデルのトレーニングとその事前トレーニングに費やされる合計時間に匹敵します。
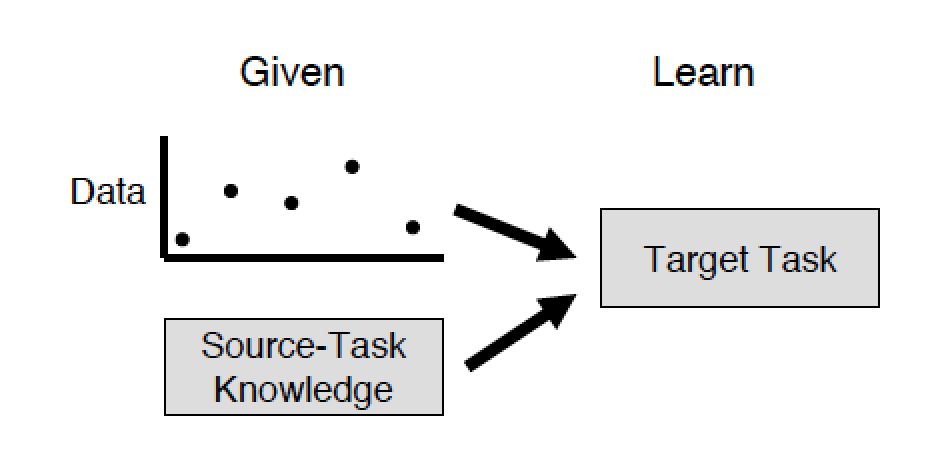
ここで、2つのタスクがあり、おそらく異なる人々がそれらを解決したと想像してください。 そのうちの1つは、他のモデル(ソースタスク)のモデルの一部を使用して、ゼロからモデルを作成するのにかかる時間を短縮し、そのモデル(ターゲットタスク)のパフォーマンスを向上させます。 ある問題から別の問題に知識を転送するプロセスは、転送学習です。 そして、おそらく私たちの脳はまさにそれをします。 上記の例のように、実際のタスクは舌の受容体で味を感じ、目で見ることです。 言語受容体で視覚情報を知覚するという課題が生じます。 そして、新しいニューロンを成長させたり、古い重みを失い、それらを再び訓練したりする代わりに、脳は結果を達成するために既存のニューラルネットワークをわずかに調整します。
転送学習のもう1つの機能は、古いモデルが長い間解決されているため、古いモデルから新しいモデルにのみ情報を転送できることです。 標準的なアプローチでは、問題の解決に関与するさまざまなモデルが互いに情報を交換できます。
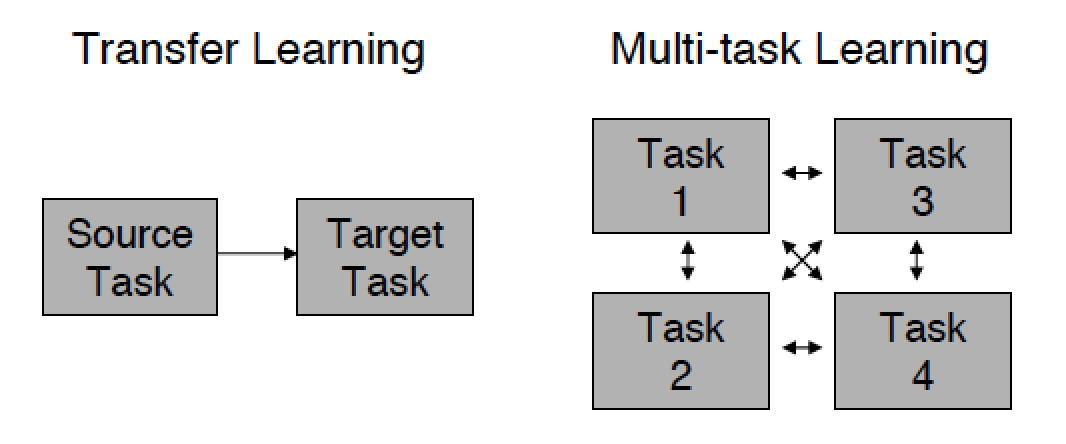
この投稿は、教師との指導のタスクに関連する転移学習の部分にのみ適用されますが、興味のある方には原本を読むことをお勧めします。 そこから、たとえば強化学習やベイジアンネットワークのトレーニングで、転送学習がニューラルネットワークよりも早く使用され始めたことを学習します。
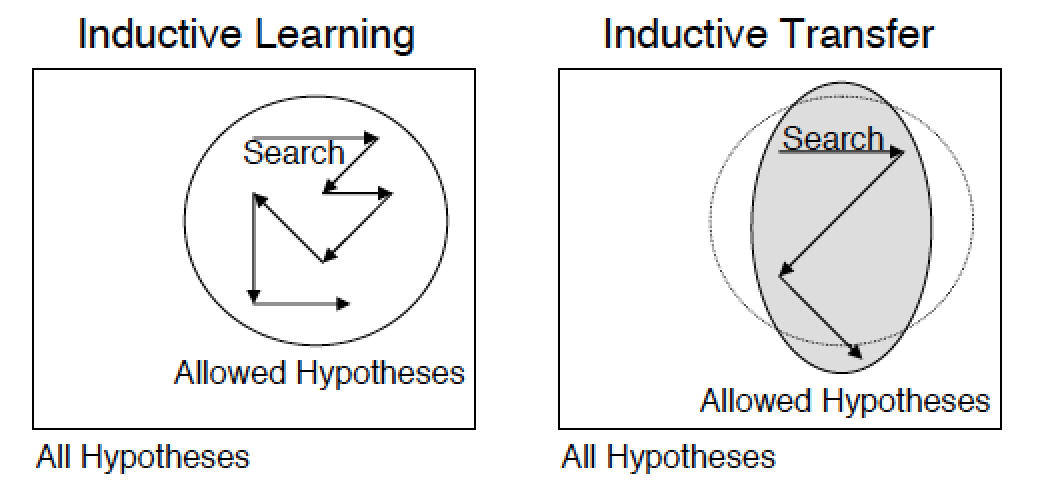
したがって、教師による学習はラベル付きの例による学習であり、例による学習プロセスは誘導学習(特定から一般への移行)と呼ばれることもあり、能力の一般化は誘導バイアスと呼ばれます。 したがって、2番目の名前転送学習- 誘導転送 。 そして、帰納的学習で知識を移転するタスクは、古いモデルの学習プロセスで蓄積された知識が新しいモデルの一般化能力に影響を与えることであると言えます(別の問題を解決する場合でも)。
知識の伝達は、正則化と見なすこともできます。これにより、検索空間は、許容可能な良好な仮説の特定のセットに制限されます。
練習する
この時点で、知識の移転のように一見目立たないアプローチを吹き込まれたことを願っています。 結局のところ、これは単に知識の伝達ではなく、神経可塑性はとてつもなく高く、この方法の最良の名前はコピーアンドペーストであると言うことができます。 それからあなたはただのプラグマティストです。 もちろん、これも良いですし、少なくとも3番目のセクションは好きでしょう。 最初のセクションで説明したものと同様のことを、人工ニューラルネットワークで繰り返してみましょう。
まず、問題を定式化します。 非常に大きな画像のセットがあるとしましょう。 類似画像の検索を整理する必要があります。 ここで2つの問題が発生します。 第一に、画像間の類似性の尺度は明らかではなく、n * m次元ベクトルからユークリッド距離を取るだけでは、結果はあまり満足のいくものではありません。 第二に、品質尺度があったとしても、データベースのフルスキャンを避けることはできず、データベースには何十億もの画像が含まれている可能性があります。
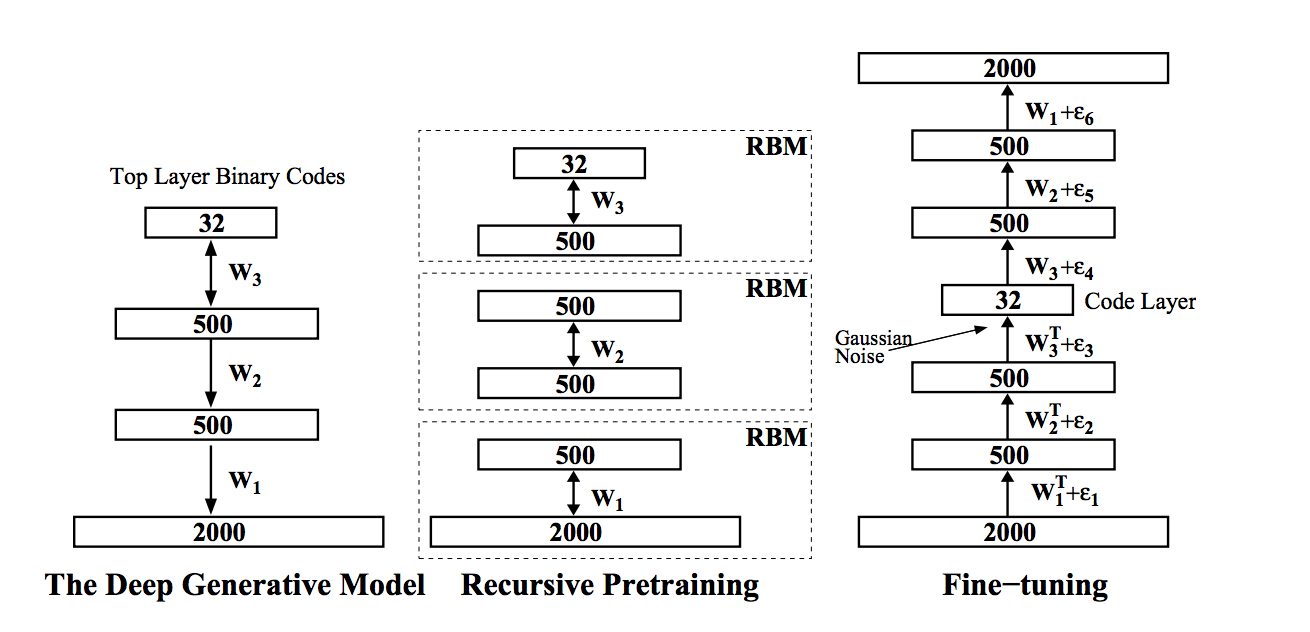
この問題を解決するために、セマンティックハッシュを使用できます。そのような方法の1つはSalakhudinovaとHintonの記事Semantic Hashingで説明されています。 彼らのアイデアは、元のデータベクトルが小さな次元のバイナリベクトルでエンコードされていることです(この場合、これは画像であり、元の記事では単語のバイナリベクトルです )。 このエンコードを使用すると、 ハミング距離を使用して、コード長から線形時間で類似の画像を検索できます。 属性の新しい空間内の意味と内容(テキスト、音楽など)が近い画像は互いに近くに配置されるため、このようなエンコードはセマンティックと呼ばれます。 このアイデアを実装するために、彼らは深い信頼ネットワークを使用しました。 その学習アルゴリズムは 、2006年にヒントンと会社によって開発されました。
- 入力ネットワークは一般に実数値(gaussian-bernoulli rbm)を取り、それらを長いバイナリベクトルにエンコードします。次の各レイヤーはバイナリコード(berboulli-bernoulli rbm)の長さを削減しようとします。
- このようなネットワークは、その独自の限定ボルツマンマシンによって下から上に順番に事前にトレーニングされ、次の各ネットワークは前のネットワークの出力を入力データとして使用します。
- 次に、ネットワークは逆の順序で展開され、入力でわずかにノイズの多いベクトルを受け取るディープオートエンコーダーとしてトレーニングされ、元のノイズのないイメージを復元しようとします。 このステップはファインターニングと呼ばれます。
- 結局のところ、オートエンコーダーの中央にあるバイナリイメージは、入力イメージからの目的のバイナリハッシュになります。
これは素晴らしいモデルのように思えますが、原則として、ヒントンのおかげで問題は解決されたと判断しました。 私はNVIDIA Tesla K20で事前トレーニングを開始し、数日待ちましたが、すべてがヒントンが述べているほどバラ色ではないことが判明しました。 写真が大きいか、ガウス・ベルヌーリrbmを使用し、記事がポアソン・ベルヌーリrbmを使用しているためか、データの特異性のためか、一般的にはあまり教えなかったためです。 しかし、どういうわけか私はもう待たなかった。 そして、 Maxim Milakovのアドバイスを思い出しました。畳み込みネットワークを使用することと、彼のプレゼンテーションの1つから学んだ用語転送です。 もちろん、写真の寸法を圧縮して色を定量化することから、コンピュータービジョンの古典的な兆候まで、そしてそれらを視覚的な単語のバッグに結合することまで、他のオプションがありました。 しかし、いったん深層学習の道に入ると、それをオフにするのはそれほど簡単ではなく、学習の約束を移すボーナス(特に時間の節約)は私を欺きました。
2014 ImageNetコンテストで優勝した冒頭で言及したVGGグループは、 非営利目的の使用のために無料でアクセスできるようにトレーニング済みのニューラルネットワークをレイアウトしていることが判明したため、調査目的でダウンロードしました。
一般に、 ImageNetは競争相手であるだけでなく、100万を超える実際の画像を含む画像データベースでもあります。 各画像は、1000のクラスのいずれかに割り当てられます。 セットはクラスごとにバランスが取れています。つまり、クラスごとに1000を超える画像があります。 オックスフォードの男たちは、Localization and Classificationのノミネートを獲得しました。 画像には複数のオブジェクトが存在する可能性があるため、評価は、モデルバージョンに応じて上位5つの最も可能性の高いバリアントに正解があるかどうかに基づいています。 下の画像では、imagenetの写真にあるモデルの1つの例を見ることができます。 ダルメシアンの面白い間違いに注意してください。残念ながら、モデルはチェリーを見つけられませんでした。

データセットがこのように変動するため、ネットワーク内のどこかに効果的な特徴抽出機能と、画像がどのクラスに属するかを決定する分類機能があると仮定するのは論理的です。 この非常に抽出器を取得し、分類器から分離し、それを使用して、意味ハッシュに関する記事から深い自動エンコーダーをトレーニングしたいと思います。
VGGニューラルネットワークは、 Caffe形式でトレーニングおよび保存されます。 ディープラーニング用の非常にクールなライブラリであり、最も重要なこと-習得が容易なため、よく理解することをお勧めします。 caffeを使用してVGGネットワークをトレパニングする前に、ネットワーク自体を一gすることをお勧めします。 詳細が興味深い場合は、元の記事- 大規模画像認識用の非常に深い畳み込みネットワーク (名前は既にネットワークの深さを暗示しています)をお勧めします。 また、畳み込みネットワークにまったく精通していない人は、先に進む前に少なくともロシア語版ウィキペディアを読む必要があります。5〜10分以上かかることはありません(またはHabréの説明があります )。
そのため、記事とコンテストのために、著者はいくつかのモデルを訓練しました。
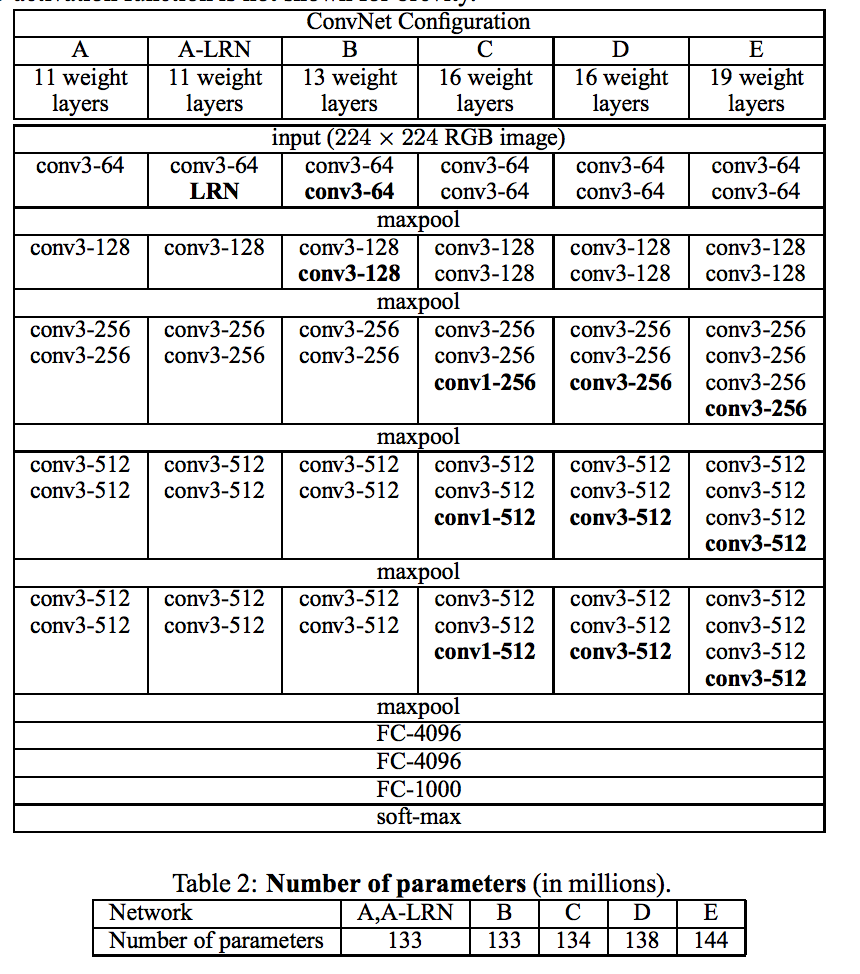
彼らのページで、彼らはオプションDとEを投稿しました。実験のために、最初の16層が畳み込みで、最後の3層が完全に接続されたEの19層バージョンを取ります。 最後の3つのレイヤーは画像のサイズに敏感であるため、実験では、よく考えずに、高レベルのサインを削除したことを考慮して、それらを捨てて最初の16のレイヤーを残しました。
caffeライブラリは、Google Protocol Buffersを使用してモデルを記述します。ネットワークの完全な記述は次のとおりです。
19層モデル
name: "VGG_ILSVRC_19_layers" input: "data" input_dim: 10 input_dim: 3 input_dim: 224 input_dim: 224 layers { bottom: "data" top: "conv1_1" name: "conv1_1" type: CONVOLUTION convolution_param { num_output: 64 pad: 1 kernel_size: 3 } } layers { bottom: "conv1_1" top: "conv1_1" name: "relu1_1" type: RELU } layers { bottom: "conv1_1" top: "conv1_2" name: "conv1_2" type: CONVOLUTION convolution_param { num_output: 64 pad: 1 kernel_size: 3 } } layers { bottom: "conv1_2" top: "conv1_2" name: "relu1_2" type: RELU } layers { bottom: "conv1_2" top: "pool1" name: "pool1" type: POOLING pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layers { bottom: "pool1" top: "conv2_1" name: "conv2_1" type: CONVOLUTION convolution_param { num_output: 128 pad: 1 kernel_size: 3 } } layers { bottom: "conv2_1" top: "conv2_1" name: "relu2_1" type: RELU } layers { bottom: "conv2_1" top: "conv2_2" name: "conv2_2" type: CONVOLUTION convolution_param { num_output: 128 pad: 1 kernel_size: 3 } } layers { bottom: "conv2_2" top: "conv2_2" name: "relu2_2" type: RELU } layers { bottom: "conv2_2" top: "pool2" name: "pool2" type: POOLING pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layers { bottom: "pool2" top: "conv3_1" name: "conv3_1" type: CONVOLUTION convolution_param { num_output: 256 pad: 1 kernel_size: 3 } } layers { bottom: "conv3_1" top: "conv3_1" name: "relu3_1" type: RELU } layers { bottom: "conv3_1" top: "conv3_2" name: "conv3_2" type: CONVOLUTION convolution_param { num_output: 256 pad: 1 kernel_size: 3 } } layers { bottom: "conv3_2" top: "conv3_2" name: "relu3_2" type: RELU } layers { bottom: "conv3_2" top: "conv3_3" name: "conv3_3" type: CONVOLUTION convolution_param { num_output: 256 pad: 1 kernel_size: 3 } } layers { bottom: "conv3_3" top: "conv3_3" name: "relu3_3" type: RELU } layers { bottom: "conv3_3" top: "conv3_4" name: "conv3_4" type: CONVOLUTION convolution_param { num_output: 256 pad: 1 kernel_size: 3 } } layers { bottom: "conv3_4" top: "conv3_4" name: "relu3_4" type: RELU } layers { bottom: "conv3_4" top: "pool3" name: "pool3" type: POOLING pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layers { bottom: "pool3" top: "conv4_1" name: "conv4_1" type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: "conv4_1" top: "conv4_1" name: "relu4_1" type: RELU } layers { bottom: "conv4_1" top: "conv4_2" name: "conv4_2" type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: "conv4_2" top: "conv4_2" name: "relu4_2" type: RELU } layers { bottom: "conv4_2" top: "conv4_3" name: "conv4_3" type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: "conv4_3" top: "conv4_3" name: "relu4_3" type: RELU } layers { bottom: "conv4_3" top: "conv4_4" name: "conv4_4" type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: "conv4_4" top: "conv4_4" name: "relu4_4" type: RELU } layers { bottom: "conv4_4" top: "pool4" name: "pool4" type: POOLING pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layers { bottom: "pool4" top: "conv5_1" name: "conv5_1" type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: "conv5_1" top: "conv5_1" name: "relu5_1" type: RELU } layers { bottom: "conv5_1" top: "conv5_2" name: "conv5_2" type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: "conv5_2" top: "conv5_2" name: "relu5_2" type: RELU } layers { bottom: "conv5_2" top: "conv5_3" name: "conv5_3" type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: "conv5_3" top: "conv5_3" name: "relu5_3" type: RELU } layers { bottom: "conv5_3" top: "conv5_4" name: "conv5_4" type: CONVOLUTION convolution_param { num_output: 512 pad: 1 kernel_size: 3 } } layers { bottom: "conv5_4" top: "conv5_4" name: "relu5_4" type: RELU } layers { bottom: "conv5_4" top: "pool5" name: "pool5" type: POOLING pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layers { bottom: "pool5" top: "fc6" name: "fc6" type: INNER_PRODUCT inner_product_param { num_output: 4096 } } layers { bottom: "fc6" top: "fc6" name: "relu6" type: RELU } layers { bottom: "fc6" top: "fc6" name: "drop6" type: DROPOUT dropout_param { dropout_ratio: 0.5 } } layers { bottom: "fc6" top: "fc7" name: "fc7" type: INNER_PRODUCT inner_product_param { num_output: 4096 } } layers { bottom: "fc7" top: "fc7" name: "relu7" type: RELU } layers { bottom: "fc7" top: "fc7" name: "drop7" type: DROPOUT dropout_param { dropout_ratio: 0.5 } } layers { bottom: "fc7" top: "fc8" name: "fc8" type: INNER_PRODUCT inner_product_param { num_output: 1000 } } layers { bottom: "fc8" top: "prob" name: "prob" type: SOFTMAX }
記述されたトレパネーションを作成するには、 fc6 (完全接続層)から始まるモデル記述のすべての層を削除するだけで十分です。 ただし、ネットワーク出力は上から無制限になることに注意してください。 アクティベーション関数は、 修正された線形単位です。
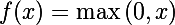
このような問題は、ネットワーク出力からシグモイドを取得することで簡単に解決できます。 多くのニューロンが0または大きな数になることを期待できます。 次に、シグモイドを取得した後、多くの単位と0.5を取得します(0からのシグモイドは0.5です)。 得られた値を0から1の範囲で正規化すると、ニューロンの活性化の確率として解釈でき、それらのほとんどすべてがゼロまたは1の領域になります。 ニューロンの活性化の確率は、画像にサインが存在する確率として解釈されます(たとえば、人間の目がそこにあります)。
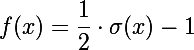
私の場合、このようなネットワークの典型的な答えは次のとおりです。
最後の畳み込み層からの正規化されたシグモイド
0.0
0.0
0.0
0.0
0.0
0.0
1.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.994934
0.0
0.0
0.999047
0.829219
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.997255
0.0
0.0
0.0
0.0
0.0
0.0
0.0
1.0
1.0
0.0
0.999382
0.0
0.0
0.0
0.0
0.988762
0.0
0.0
1.0
1.0
0.0
1.0
1.0
0.0
1.0
1.0
1.0
1.0
1.0
0.0
1.0
1.0
0.0
0.0
1.0
1.0
0.0
1.0
1.0
0.0
0.0
0.0
0.0
0.0
0.847886
0.0
0.0
0.0
0.0
0.957379
0.0
0.0
0.0
0.0
0.0
1.0
0.999998
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
1.0
0.999999
0.0
0.54814
0.739735
0.0
0.0
0.0
0.912179
0.0
0.0
0.78984
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.681776
0.0
0.0
0.991501
0.0
0.999999
0.999152
0.0
0.0
1.0
0.0
0.0
0.0
0.0
0.999996
1.0
0.0
1.0
1.0
0.0
0.880588
0.0
0.0
0.0
0.0
0.0
0.0
0.836756
0.995515
0.0
0.999354
0.0
1.0
1.0
0.0
1.0
1.0
0.0
0.999897
0.0
0.953126
0.0
0.0
0.999857
0.0
0.0
0.937695
0.999983
1.0
0.0
0.0
0.0
0.0
0.0
1.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
1.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.994934
0.0
0.0
0.999047
0.829219
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.997255
0.0
0.0
0.0
0.0
0.0
0.0
0.0
1.0
1.0
0.0
0.999382
0.0
0.0
0.0
0.0
0.988762
0.0
0.0
1.0
1.0
0.0
1.0
1.0
0.0
1.0
1.0
1.0
1.0
1.0
0.0
1.0
1.0
0.0
0.0
1.0
1.0
0.0
1.0
1.0
0.0
0.0
0.0
0.0
0.0
0.847886
0.0
0.0
0.0
0.0
0.957379
0.0
0.0
0.0
0.0
0.0
1.0
0.999998
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
1.0
0.999999
0.0
0.54814
0.739735
0.0
0.0
0.0
0.912179
0.0
0.0
0.78984
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.681776
0.0
0.0
0.991501
0.0
0.999999
0.999152
0.0
0.0
1.0
0.0
0.0
0.0
0.0
0.999996
1.0
0.0
1.0
1.0
0.0
0.880588
0.0
0.0
0.0
0.0
0.0
0.0
0.836756
0.995515
0.0
0.999354
0.0
1.0
1.0
0.0
1.0
1.0
0.0
0.999897
0.0
0.953126
0.0
0.0
0.999857
0.0
0.0
0.937695
0.999983
1.0
0.0
0.0
0.0
0.0
0.0
1.0
0.0
0.0
0.0
カフェでは、この問題は次のように解決されています。
layers { bottom: "pool5" top: "sigmoid1" name: "sigmoid1" type: SIGMOID }
CaffeはPythonラッパーを実装し、次のコードはネットワークを初期化して正規化します。
caffe.set_mode_gpu() net = caffe.Classifier('deploy.prototxt', 'VGG_ILSVRC_19_layers.caffemodel', channel_swap=(2,1,0), raw_scale=255, image_dims=(options.width, options.height)) #.................. out = net.forward_all(**{net.inputs[0]: caffe_in}) out = out['sigmoid1'].reshape(out['sigmoid1'].shape[0], np.prod(out['sigmoid1'].shape[1:])) out = (out - 0.5)/0.5
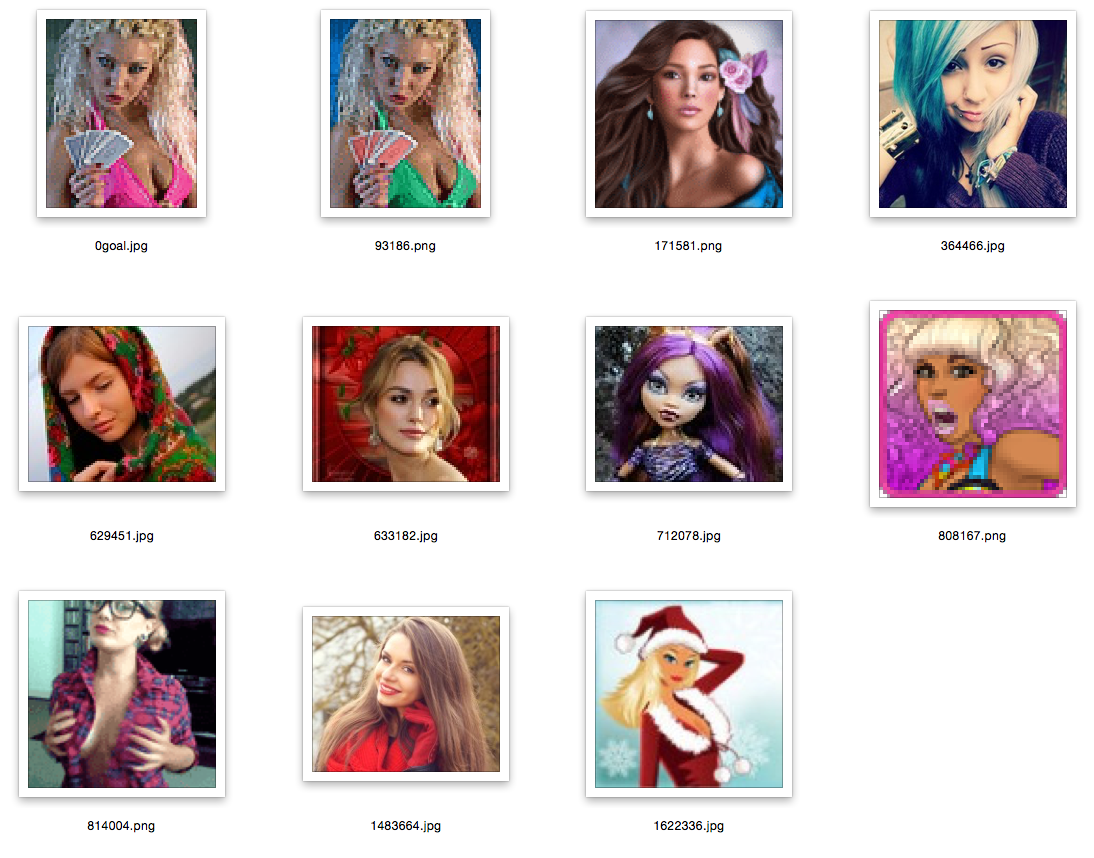
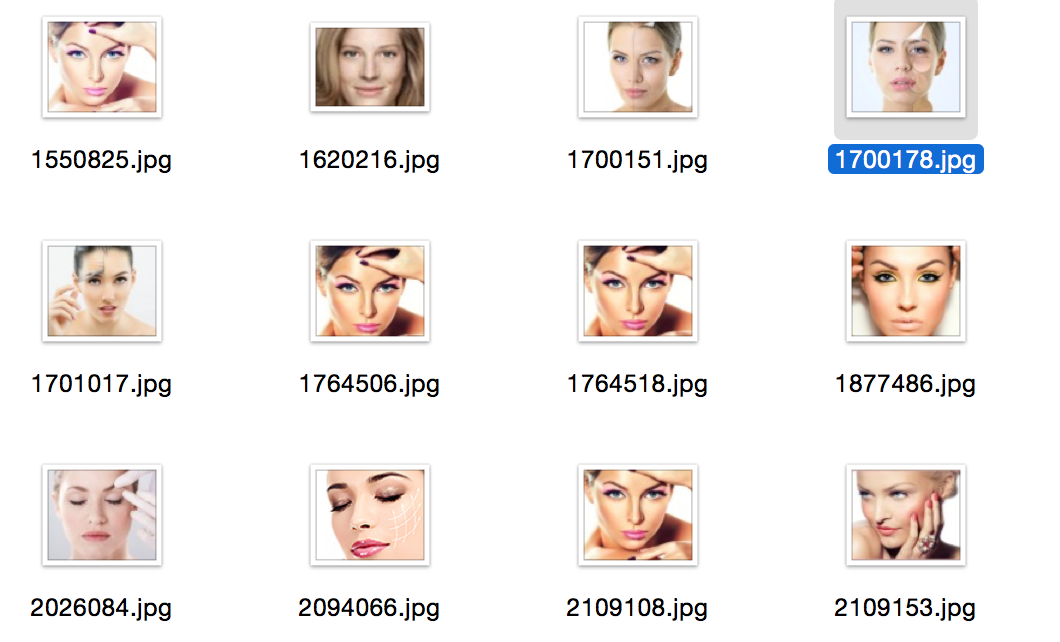
したがって、現時点では、高次元のベクトル(私の場合は4608)を含む画像のバイナリ(またはほぼ)表現を手にしています。これらの表現を圧縮するために、Deep Befief Networkをトレーニングする必要があります。 結果のモデルはさらに深いネットワークになりました。 DBNが数日間学習するのを待たずに、検索実験を行ってみましょう。ランダムな画像を選択し、ハミング距離に関して最も近い画像をいくつか検索します。 これはすべて、生の特徴、高次元のベクトル、符号の重み付けなしであることに注意してください。
説明:最初の写真はリクエストの写真、データベースからのランダムな画像です。 残りは彼女に最も近い。
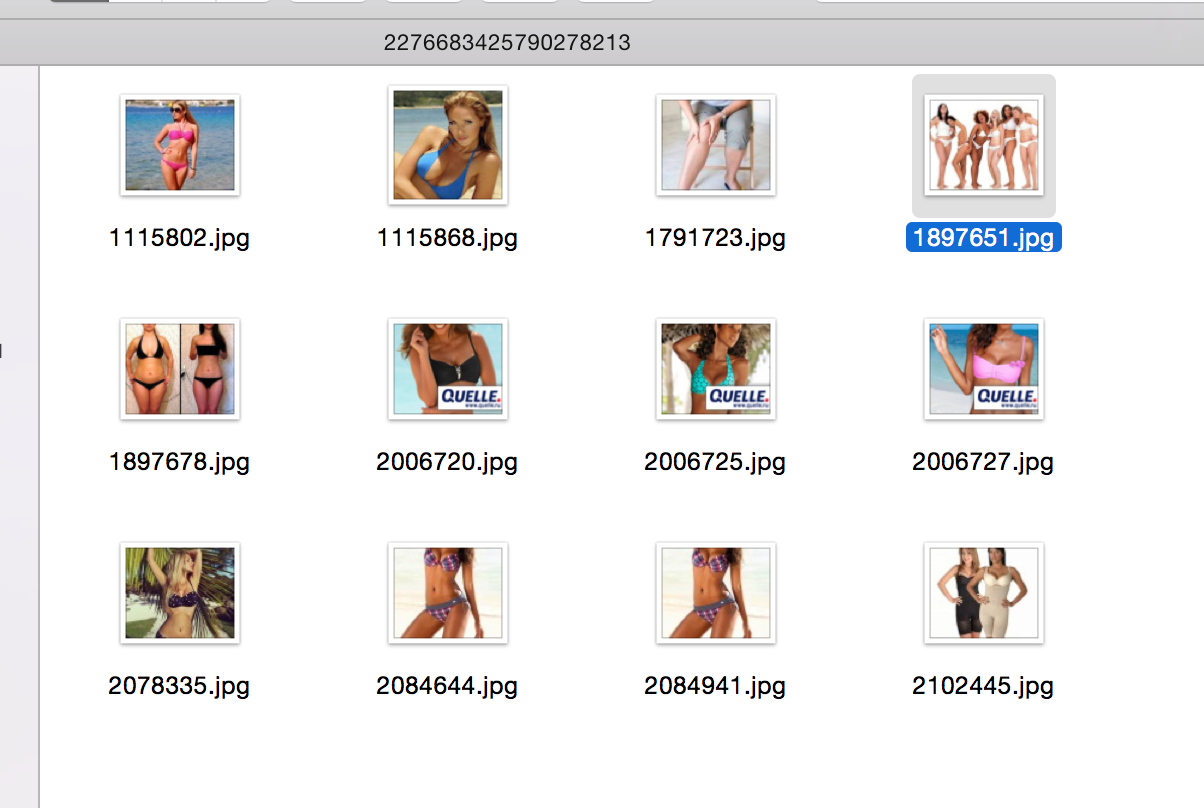
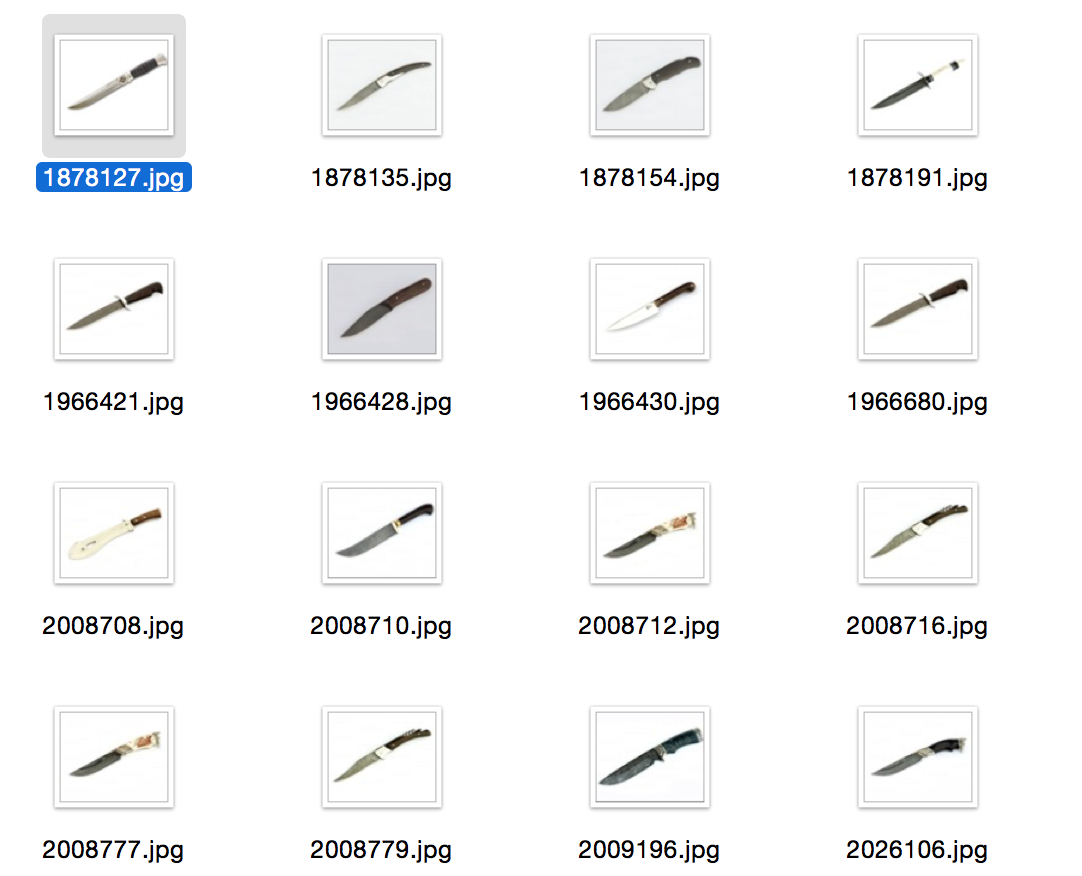
ネタバレの他の例 
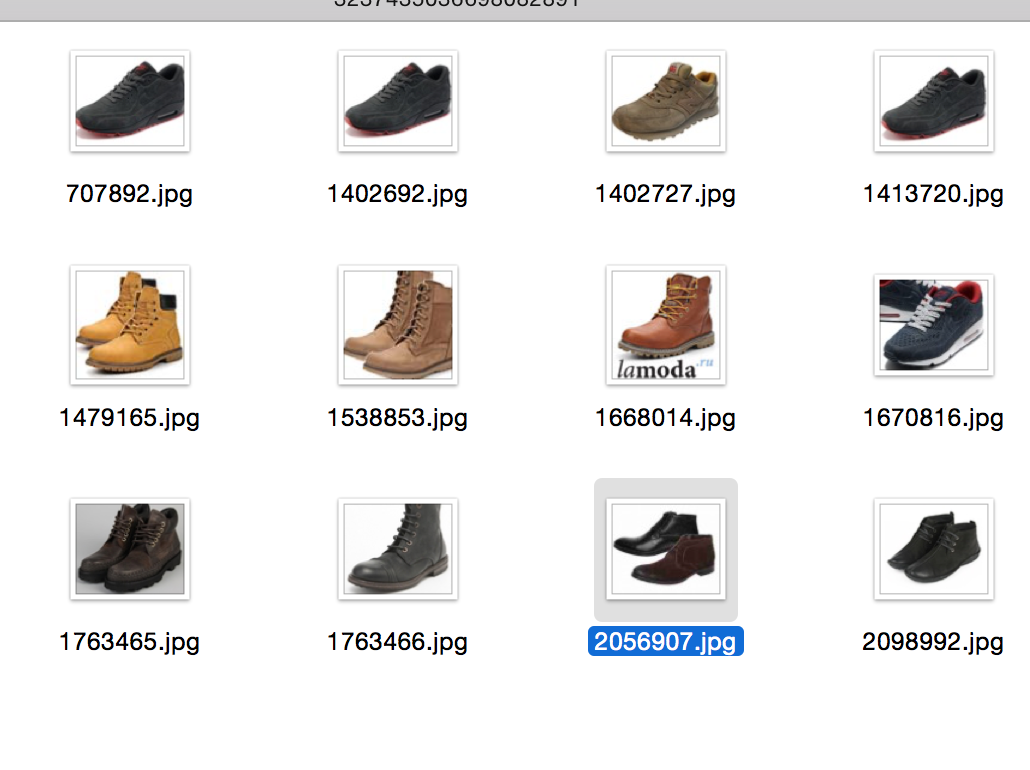

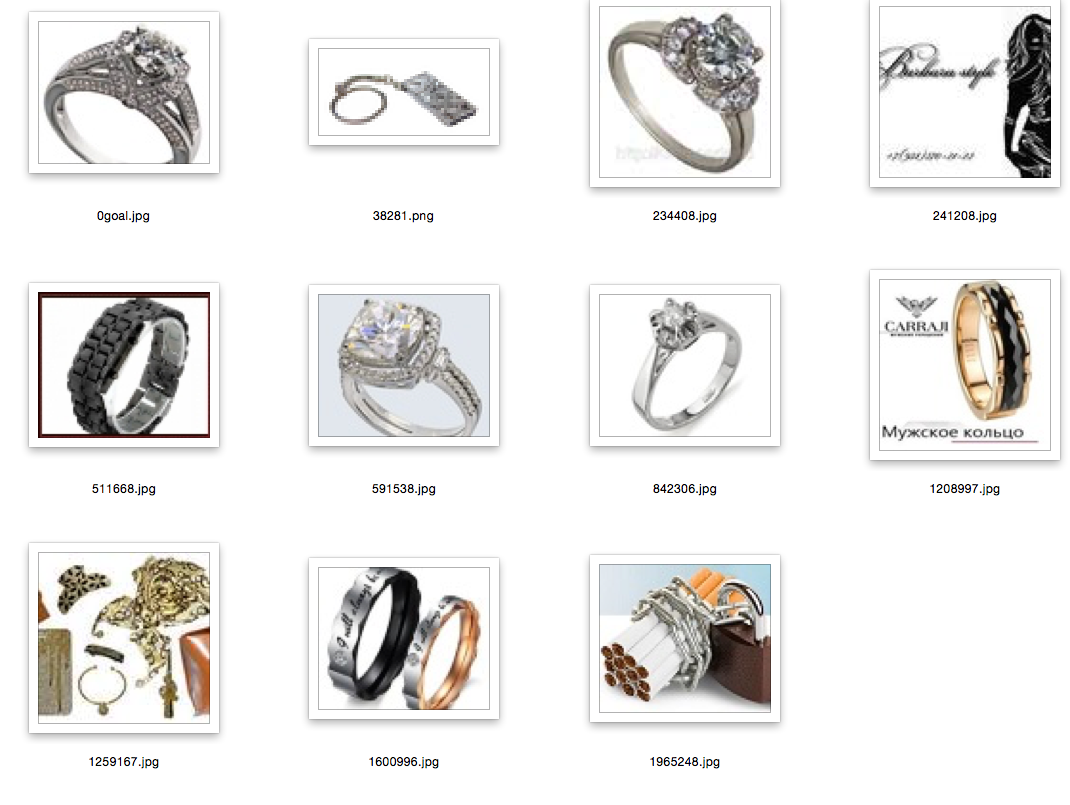
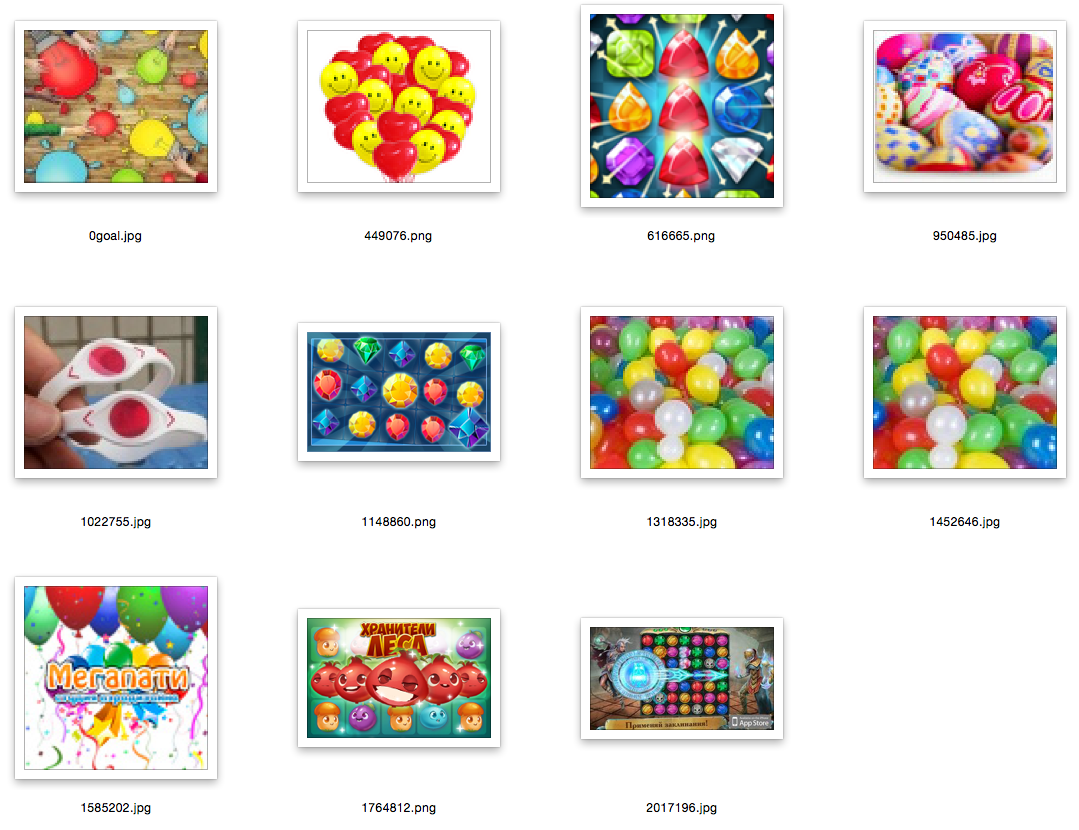

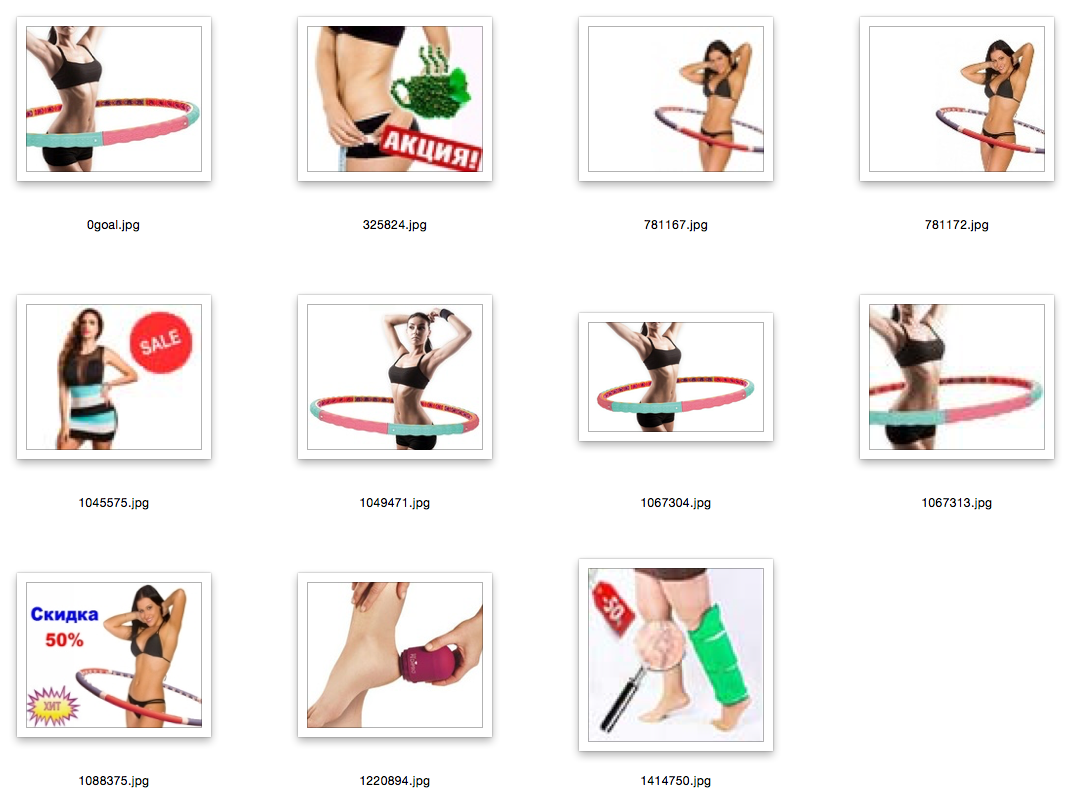











結論と参考文献
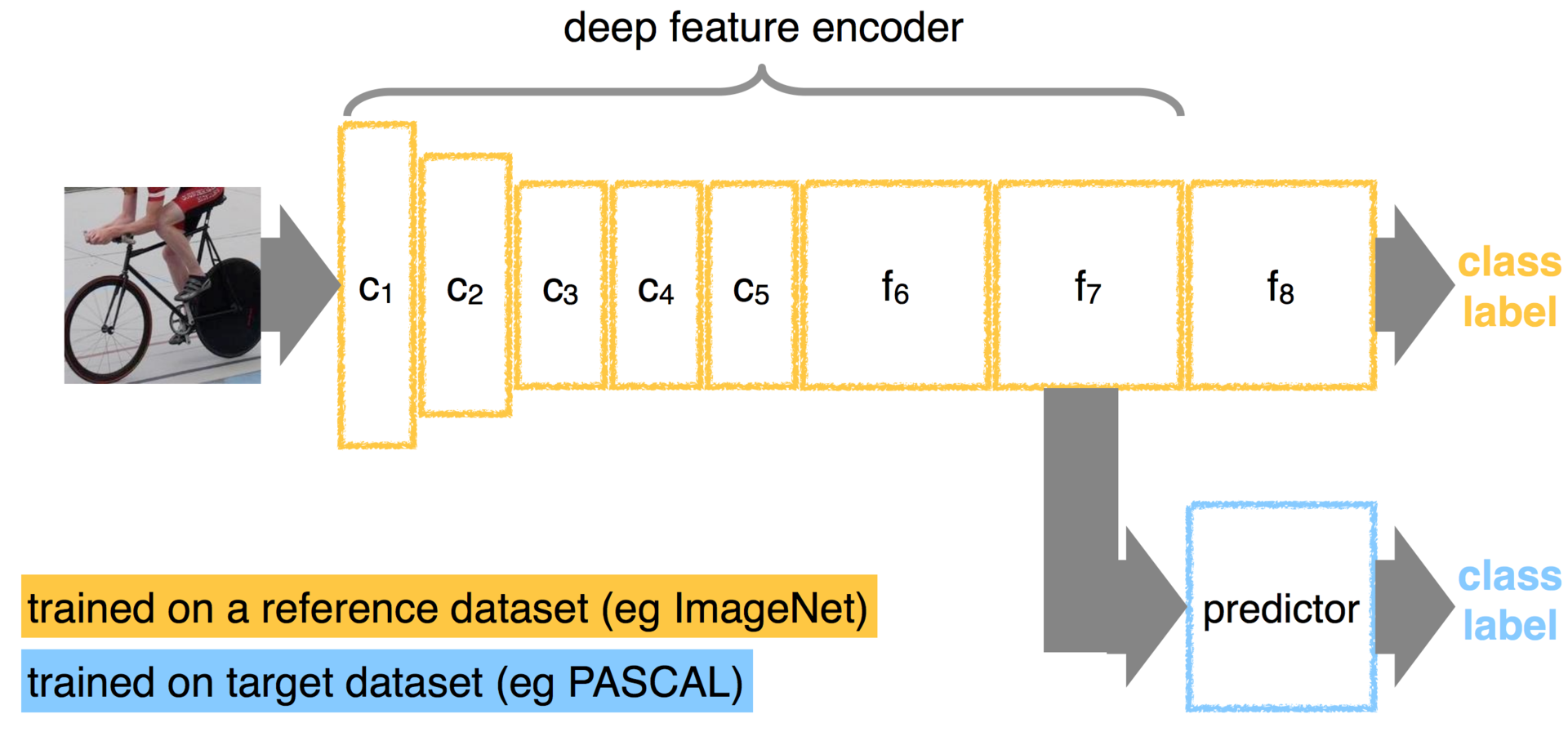
静的なレイヤーを転送するだけでなく、独自の方法でそれらをトレーニングする例を簡単に思いつくことができると思います。 別のネットワークを使用してネットワークの一部を初期化してから、クラスで再トレーニングできるとしましょう。
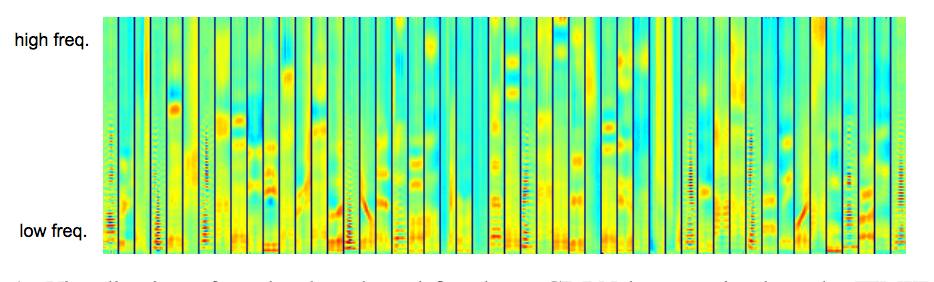
そして、最初の部分で説明した実験に近いものを試してみると? お願い:畳み込みの深い信念ネットワークを使用してオーディオ信号から特徴を抽出するサンプル記事です。 訓練された畳み込みを使用してcDBNの重みを初期化しないのはなぜですか? なぜこのようなスペクトログラムは画像ではなく、なぜ低レベルの機能が動作しないのか:
自然言語処理を試し、転移学習を試してみたい場合は、LeCuneの適切な記事をご覧ください 。 もちろん、テキストも画像として表示されます。
一般的に、転移学習は素晴らしいことであり、 カフェはディープラーニングのためのクールなライブラリです。
テキストには多くのリンクがありますが、ここでそれらのいくつかを示します。


