角度検出器

画像処理、特に特異点を扱うことに興味があります。 角度検出器に関する情報を探して、ロシア語でこれらのアルゴリズムの十分に大きな概要を見つけられませんでした。 したがって、この記事を書いて状況を修正することにしました。 記事の概要は次のとおりです。

• はじめに
• 特徴点のプロパティ
• 角度検出器
  
  
  • モラベック
  • ハリス
  • したち
  • Forstner
  • スーザン
  • トレイコビッチ
  • 速い
  • CSS
  • グローバルおよびローカルの曲率特性に基づく検出器
  • CPDA
• 結論

はじめに

画像から解釈された情報を抽出するには、画像のローカルフィーチャにバインドする必要があります。 画像内の特異点を強調表示することができます。 画像の特異点mまたは点の特徴（英語の点の特徴、キーポイント、特徴）は、その近傍o（m）が特異点oの他の近傍にある他の画像点o（n）の近傍と区別できる画像点です。 ₂ （m） 。 ほとんどのアルゴリズムの画像ポイントの近くでは、サイズが5x5ピクセルの長方形のウィンドウが使用されます。 特異点を決定するプロセスは、検出器と記述子を使用して実現されます。



検出器は、画像から特異点を抽出する方法です。 検出器は、画像変換に関して同じ特異点を見つけることの不変性を提供します。



記述子は、特異点のセットの残りの部分と区別する特異点の識別子です。 次に、記述子は、画像変換に関して特異点間の対応を見つけることの不変性を保証する必要があります[1]。

特徴点のプロパティ

1992年、ハラリックとシャピル[10]は、特異点に関する次の要件を次のプロパティの形式で特定しました。

• 明確さ-特定のポイントが背景からはっきりと目立つようにし、その近くで区別できるようにする必要があります。
• 不変性 -特異点の定義は、アフィン変換から独立している必要があります。
• 安定性 -特定のポイントの定義は、ノイズとエラーに耐える必要があります。
• 一意性 -局所的な識別可能性に加えて、特定のポイントは、繰り返しパターンの識別可能性を改善するためにグローバルな一意性を持たなければなりません。
• 解釈可能性 -特別なポイントを定義して、対応を分析し、画像から解釈された情報を識別するために使用できるようにする必要があります。

[5] Tuytelaars and Mikolajczyk（2006）で、特異点を持たなければならない以下の特性を区別したことは興味深い。

• 再現性 -特定のポイントは、視点と照明の変化にもかかわらず、シーンまたは画像オブジェクトの同じ場所にあります。
• 識別性/情報性（識別性/情報性） -特異点の強調表示と一致を可能にするために、特異点の近傍には互いに大きな違いがあるはずです。
• 局所性 -異なる視点で撮影された2つの画像間の幾何学的および測光的歪みに対する感度の可能性を減らすために、特定の点が画像の小さな領域を占める必要があります。
• 数量 -検出された特殊ポイントの数は、小さなオブジェクトを検出するのに十分な大きさでなければなりません。 ただし、特異点の最適な数は対象領域によって異なります。 理想的には、検出された特異点の数は、単純で直感的なしきい値を使用して適応的に決定する必要があります。 特異点の位置の密度は、コンパクトな表現を確保するために、画像の情報内容を反映する必要があります。
• 精度 -検出された特異点は、元の画像と異なるスケールで撮影されたものの両方で、正確にローカライズする必要があります。
• 効率性 -イメージ内の特別なポイントを検出する時間は、タイムクリティカルなアプリケーションで許容できるはずです。

一般に、これらのプロパティは[10]と交差しますが、解釈が異なります。

角度検出器

さまざまなアプリケーション向けに設計された特異点を決定するための多くのアルゴリズムがあります。 この記事では、角度検出器（またはコーナー検出器とも呼ばれる）に注意を払います。



コーナーは、2つ以上の面から形成される特異点であり、面は通常、異なるオブジェクトおよび/または同じオブジェクトの一部の間の境界を定義します。 [2]別の言い方をすれば、角度とは、近傍の強度が中心（x、y）に対して変化する点であると言えます。 角度は、周囲の画像ポイントの座標と明るさの変化によって決まります。 このようなポイントの主な特性は、イメージグラデーションのコーナー付近の領域で2つの支配的な方向が支配的であるため、それらを区別できるようにすることです。 勾配は、画像強度関数I（x、y）の最も速い増加の方向を示すベクトル量です。 画像は離散的であるため、勾配ベクトルはxおよびy軸に沿った偏導関数によって決定され、隣接する画像ポイントの強度の変化によって決定されます。 ほとんどの方法は、2次導関数に依存する角度を考慮するため、一般的に、方法はノイズに敏感です。



交差する面の数に応じて、異なるタイプのコーナーがあります：L-、Y-（またはT-）、およびX-連結[3]（スイープ連結コーナー[2]でも区別するものもあります）。 異なるコーナー検出器は、これらの種類のコーナーのそれぞれに異なる応答をします。







特異点の決定へのアプローチは、3つのカテゴリに分類できます[10]。

1. イメージ強度ベース：特徴点は、イメージピクセル強度値から直接計算されます。
2. 画像の等高線の使用：等高線を抽出し、曲率の最大値を持つ場所を探すか、等高線の多角形近似を行い、交差を決定します。 3つ以上のエッジが交差する場所では抽出が不正確になることが多いため、これらの方法は交差点の交差点に敏感です。
3. モデルの使用に基づいて：強度を持つモデルがパラメーターとして使用され、テンプレート画像に合わせてサブピクセルの精度に調整されます。 使用されるパターンに応じて、特殊タイプの特殊ポイント（たとえば、L連結角度）での使用は制限されています。

実際には、画像強度に基づく方法は、広く使用されている最も一般的な方法です。

次に、角度を決定する特異点の主な検出器の説明を検討します。 次に、検出器の比較表が、さまざまな状況への適用性に関する結論とともに提示され、最後に、コーナー検出器が適用された画像が提示されます。

モラベック

特別なポイントを使用した画像バインディングの研究は、Moravec検出器で始まりました（Moravec、1977）。 Moravec検出器は最もシンプルです。 著者は 、ウィンドウWが 8方向（水平、垂直、対角線）に1ピクセルシフトされたときの、注目ポイントに対する正方形ウィンドウW （通常3x3、5x5、7x7ピクセル）の明るさの変化を考慮します[4]。 アルゴリズム：

1. 画像の各ピクセル（x、y）について、強度の変化を計算します
   
   
   
   
   
   
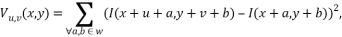
2. 推定関数を計算して、画像の各ピクセル（x、y）で角度を見つける確率のマップを作成します 。 つまり、強度の最小の変化が対応する方向が決定されます。 コーナーには隣接するエッジが必要です。
3. C（x、y）の値がしきい値Tを下回るピクセルを切り取ります。
4. 非最大抑制局所最大値検索手順を使用して、重複した角度を削除します。 受信したすべてのゼロ以外のマップ要素は、画像の角に対応しています。

Moravec検出器には、8方向のウィンドウ変位の異方性の特性があります。 検討中の検出器の主な欠点は、回転変換に対する不変性の欠如と、多数の対角線エッジが存在する場合の検出エラーの発生です[2]。

ハリス

研究により、L結合角の最も最適な検出器は、よく知られているHarris検出器（Plesseyオペレーター、Harris and Stephens検出器、Plesseyオペレーター、Harris and Stephens検出器、1988年とも呼ばれます）であることが示されました[5] [6]。



HarrisとStephensは、すべての方向に異方性を導入することでMoravec検出器を改善しました。 画像の明るさの導関数は、さまざまな方向の明るさの変化を調べるために考慮されます。 彼らはいくつかの主要な方向に誘導体を導入します。



この画像Iでは 、中央（x、y）のウィンドウW （通常、ウィンドウサイズは5x5ピクセルですが、画像サイズに依存する場合があります）と（u、v）によるシフトを考慮します。







次に、シフトされたウィンドウと元のウィンドウの間の重み付き平方差（SSD）（つまり、 （u、v）だけシフトされたときのポイント（x、y）の近傍の変化）は次と等しくなります：





ここで、 w（x、y）は重み関数です（通常はガウス関数またはバイナリウィンドウが使用されます）。





M-自己相関行列：







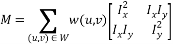
角度は、すべての可能な方向（x、y）における関数E（x、y）の大きな変化によって特徴付けられます。これは、行列Mの大きなモジュロ固有値に相当します。 固有値の場所を次の図に示します。





固有値を直接数えることは時間のかかる作業であるため、HarrisとStephen [7]によって応答測定が提案されました。



ここで、 kは経験的定数です 。

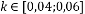したがって、 Rの値はコーナーの特異点に対して正です。 次に、見つかったしきい値Rに従ってポイントがカットオフされます（つまり、 Rの値が特定のしきい値よりも小さいポイントは考慮から除外されます）。 次に、応答関数の局所的最大値（非最大抑制）が指定された半径の近くで見つかり、コーナー特異点として選択されます。



Harris検出器は回転に対して不変であり、強度のアフィン変化に対して部分的に不変です。 欠点には、ノイズ感度と検出器の画像スケールへの依存が含まれます（この欠点を解消するには、マルチスケールのハリス検出器を使用します）。

したち

Shi-Tomasi角度検出器（Shi-TomasiまたはKanade-Tomasi、1993）は、Harris検出器とほぼ一致しますが、応答測定の計算が異なります。アルゴリズムは値を直接計算します 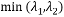、角度の検索がより安定すると想定されるため。 著者は、ルーカスとカナデの光束を分析するために同じ方程式を使用しています。 アルゴリズムの詳細は、記事[8]および[9]に記載されています。

Forstner

FörstnerとGülch（1987）は、Harris検出器と同じ角度測定を使用する方法を最初に説明しました。 彼らはより計算的に複雑な実装を使用しました[8]。 Harris検出器とは異なり、固有値は明示的に計算されます。 Förstner角度応答関数は、次のように定義されます。







また、定義を正確にするために、角度の丸さの尺度は次と等しいと見なされます。 。



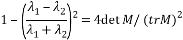Förstner検出器は、Harris検出器の機能を拡張するために実際によく使用されます-角に沿って円形の特異点を見つけます。 このアルゴリズムには、最適なローカリゼーションプロパティもあります[2]。



アルゴリズムのより詳細な説明は、 Wikipediaおよび[10]、[11]に記載されています。

スーザン

SUSANアルゴリズム（最小単値セグメント同化核）は、Smith and Brady（Smith and Brady、1997）[5]によって提案されました。







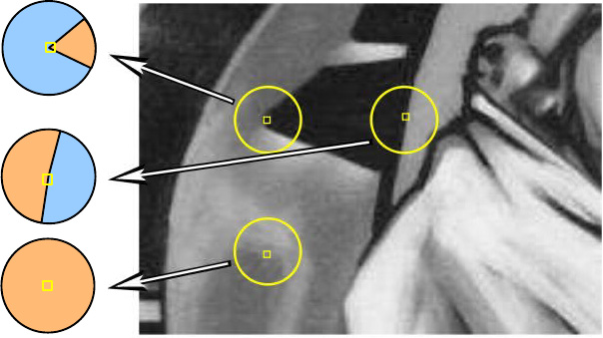
角度は、円形の近傍を類似（オレンジ）および非類似（青）のセクションに分割することによって決定されます。 角度は、同様のサイト（同様のUSAN）の相対面積が特定のしきい値を下回るローカル最小値に達する場所です。



各ピクセルについて、固定半径の円形領域が考慮されます。 ピクセルの中心はコアと呼ばれ、その強度の値が記憶されます。 他のすべてのピクセルは、コア強度の値が類似しているかどうかに応じて、類似（オレンジ）および非類似（青）の2つのカテゴリに分類されます。 円形領域の下に画像の一部が変化しない場合、同様のセクションがほぼ全体の領域を占有し、エッジではこの比率は50％に低下し、コーナーでは約25％に低下します。 したがって、角度は、同様のサイト（同様のUSAN）の相対面積が特定のしきい値を下回るローカル最小値に達する場所です。 アルゴリズムの安定性を高めるために、著者はコアに最も近いピクセルに高い重みを割り当てます。 アルゴリズムの手順は次のとおりです。

1. 円形マスクの中心をコアに配置します。
2. 円形マスク内で、次の式を使用してコアと同様の強度を持つピクセルの数を計算します（見つかったピクセルはUSANを決定します）。
   
   
   
   -マスク内のポイント。
   
   -コアセンター;
   
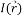   -ポイント強度 ;
   
   tは強度の差のしきい値です。
   
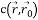   -比較の結果。
   
   
3. 次の式を使用して、幾何学的しきい値からUSANサイズを減算して、角度付きの画像を取得します。
   
   
   
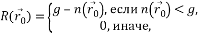
   エッジ応答の初期値です。 SUSANの原則：USANエリアが小さいほど、エッジ応答が大きくなります。
   
   gは幾何学的なしきい値です。
   
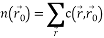   -USANのピクセル数、つまり USANエリア。
   
   
4. USANエリアの重心と互いの近接度を見つけ、誤検知を特定します。
5. 応答関数の局所的最大値（非最大抑制）を検索して特異点を選択します。

アルゴリズムは、あらゆる種類の角度に対して良好な精度を示しますが、画像がぼやけるのは不安定です。 詳細は[12]に記載されています。

トレイコビッチ

Treyakovits and Hedley（Miroslav Trajkovic and Mark Hedley、1998）の記事「Fast corner detection」では、新しいタイプの検出器-演算子Tryakovitsa [8]が紹介されました。 当初、著者は彼に最も人気のある角度検出器になり、最小限の計算コストを要求しました。 最初に、4-neighbor Trajkovic4アルゴリズムが開発されました。



検出器は、近くのピクセルを調べることでピクセルの周囲の領域をチェックします。cを調べるピクセルとし、 Pを点Nの中心の円S _N上の点とします。 点P 'は、直径がPと反対の点です。



応答関数（作成者はCRN、Corner Request Functionと呼びます）は次のように定義されます：







ここで、 Nは中心点です。

PとP 'は、点Nの周りの2つの正反対の点です。

S _N-半径3、5、7ピクセルの画像内の離散化された円。







CRN値は、中央のピクセルが直径で隣接する2つのピクセルに似ている方向がない場合、大きくなります。 任意の方向の計算が上限の境界minを与えるため、まず水平方向と垂直方向をチェックして、 R _Nの完全な計算に進むことが理にかなっているかどうかを判断します_。



Harris検出器と比較して、Trajkovic4アルゴリズムの繰り返し周波数はさらに悪いですが、ローカリゼーションはL結合角度の決定に匹敵し、他のタイプの角度よりも優れています。



短所には、この4隣接演算子が対角線エッジに誤って反応し、ノイズに敏感であるという事実が含まれます[2]。 したがって、彼らはこのTrajkovic8アルゴリズムの8接続バージョンを使用します。 Trajkovic8は、角度の計算方法がTrajkovic4と異なります。 ただし、Trajkovic8は、オブジェクトの斜めの面で誤った角度を検出します（人工画像ではうまく機能しません）。 アルゴリズムの詳細な説明は、[2]および[8]に記載されています。

速い

Rosten and Drummond（2005）は、非常に成功したFASTアルゴリズム（加速セグメントテストの機能）-加速セグメントテストの機能を導入しました。



アルゴリズムは、候補点Pの周りの16ピクセルの円（ブレゼンハムアルゴリズムによって描画された）を考慮します。 現在の考慮点Pについて、円上に強度がI _P + tより大きい、またはすべての強度がI _P -tより小さいN個の隣接ピクセルがある場合、点は角度です。ここで、 I _Pは点Pの強度、 tはしきい値です。 次に、1、5、9、13の番号が付けられた円の垂直および水平ポイントの強度をポイントPの強度と比較する必要があります（できる限り早く誤った候補をカットするため）。 これらのポイントのうち3つで条件I _Pi > _IP + tまたはI _Pi < _IP + t、i = 1、..、4が満たされる場合、16点すべてに対して完全なテストが実行されます[13]。 実験により、特異点が安定して検出されるNの最小値はN = 9であることが示されました。





最初は、元のアルゴリズムはFAST-12でした。 アルゴリズムには、ツリーベースのFAST-9およびFAST-12（ツリーベースのFAST-9およびFAST-12）の変更があります。



元のアルゴリズムにはいくつかの欠点があります。たとえば、特定の近傍の近くにいくつかの特別な点が見つかる場合があり、アルゴリズムの有効性は画像処理とピクセル分布の順序に依存します。



[14]で、著者のEdward Rosten、Reid Porter、およびTom Drummond（2008）は、FASTアルゴリズムの改良点、つまり機械学習を使用して特異点を決定することを導入しました。



彼らはこのアルゴリズムをFAST-ER（ER-Enhanced Repeatability）と呼びました。 このアルゴリズムは、再現性の特性に対して安定しています。異なる角度から見た同じシーンに、同じオブジェクトに属する特異点があります。



このアルゴリズムは、FAST（48ピクセル）よりも1ピクセル以上の円リングを使用します。 著者は、ID3アルゴリズムを使用して、決定木を使用して特異点（候補点が特別であるかどうか）を分類します。 ID3アルゴリズムは、ピクセルが処理される順序を最適化し、最も計算効率の高い検出器をもたらします。







決定木のコスト関数は次のように計算されます。







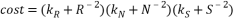
Rは再現性の尺度です。

Nは、検出された特異点の数です。

Sは、決定木のノードの数です。



詳細は[14]で説明されています。



FAST-ERはFASTよりも優れていますが、速度は遅くなります。 著者らは、再現性の点でFAST-ER検出器が最適であると結論付けました。

CSS

Rattarangsi and Chin（1992）[15]は、平面曲線上の角度を検出する曲率スケール空間（CSS）に基づくアルゴリズムを提案しました。 CSSは、さまざまなスケールで平坦な曲線上の不変の幾何学的特徴を抽出するのに適しています。



アルゴリズムは、同じ画像の複数のスケールを使用して特異点を決定します。 ただし、計算が複雑であり、円形領域で誤った角度を検出します。 [16]



Farzin Mokhtarian and Riku Suomela（1998）[17]は、ノイズ耐性のアルゴリズムを改善しました。 このアルゴリズムは白黒画像に適用され、次の手順が含まれます。

1. 画像にCanny境界検出器を適用し、バイナリ境界マップを取得します。
2. バイナリマップから境界線の輪郭を選択します。 等高線の端で他との隣接性を確認し、隣接している場合は、接続に境界線を補充します。 輪郭の端が境界線に接続している場合、この点をT接続角度としてマークします。
3. 最大スケールσhighで各輪郭の曲率を計算します。 曲率の​​値がしきい値tを超え、隣接する極小値の2倍である場合、曲率の極大値の初期値を入力します。
4. ローカリゼーションプロパティを改善するために、角度を最大から最小に降順でソートします。
5. Tで接続されたコーナーを他のコーナーと比較し、それらが互いに近い場合は、いずれかのコーナーを削除します。

この画像は、顔の間隔が2つの場合を示しています。Tに接続されたギャップはTコーナーポイントとしてマークされ、輪郭の端の間のギャップが埋められます。







このアルゴリズムには、次の欠点があります。1つのスケールの画像のみを使用して角度の数を決定し（ステップ3）、複数のスケールの画像をローカライズに使用します。 その結果、アルゴリズムは、 σが大きい場合に角度をスキップし、 σが小さい場合に偽を検出します。 [16]



アルゴリズムにいくつかの改良が加えられました。2001年にF. MokhtarianとR. Suomelaの記事「曲率スケールスペースによるロバストな画像コーナー検出」（CSSの改善提案）、2008年に彼とYungの記事「Corner detector based based on global and local curveプロパティ」、およびCPDA検出器。

グローバルおよびローカルの曲率特性に基づく検出器

彼とYung（2008）は、「グローバルおよびローカル曲率特性に基づくコーナー検出器」というタイトルの記事で、CSSアルゴリズムの改善を提案しています。 彼らは、従来の計算アルゴリズムは画像の局所特性を考慮し、特定のポイントでノイズを誤って検出したり、オブジェクトの細部をスキップしたりすることが多いと主張しています。 このアルゴリズムでは、顔の曲率のレベルのグローバルプロパティとローカルプロパティのバランスが取れて、角度が抽出されます。



その結果、彼とYungは次のソリューションを提供します。

1. たとえば、Canny Canny検出器を使用して境界線を検出し、境界線のバイナリマップを取得します。
2. CSSアルゴリズムのようにパスを選択します。
3. 固定された小さなスケールの曲率値を計算し（真の角度を逃さないように）、曲率の絶対値の局所的最大値を考慮します。これは潜在的なコーナー候補としてマークされます。
4. 検討中の領域の平均曲率に基づいてしきい値を計算します。 角度候補の曲率を適応しきい値と比較して、円形角度を削除します。
5. 適応関心領域を使用して残りのコーナー候補の角度を計算し、誤った候補を削除します。
6. 開いた輪郭の端を考慮し、それらが互いに近くない場合は、角度としてマークします。

そのため、この画像は、丸い角（a）と、まだ円形ではない鈍角（b）を決定する例を示しています。 それらを決定するために、曲率の値が計算され、そのグラフが図（c）と（d）に示されています。





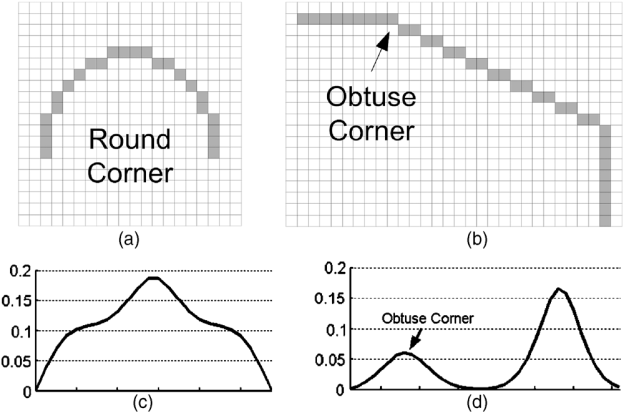
アルゴリズムの詳細は、[16]で説明されています。

CPDA

AwrangjebとLuは新しいCPDA検出器を導入しました（Chord-to-Point Distance Accumulation、2008）[18]。



σが大きいガウス分布はノイズを低減しますが、ローカリゼーションに影響を与えますが、σが小さいガウス分布はノイズに敏感です。これらの問題を解決するために、AwrangjebとLuは、HanとPostonのアイデアに基づいた適応しきい値を使用して、コードからポイントまでの距離の累積（CPDA）メソッドを提案しました。CPDAメソッドは、局所的な変化に耐える曲率の離散推定値を使用します。著者は、さまざまな長さの3つのコードを使用して、滑らかな曲線の各点で曲率の3つの正規化された離散値を推定します。[19]







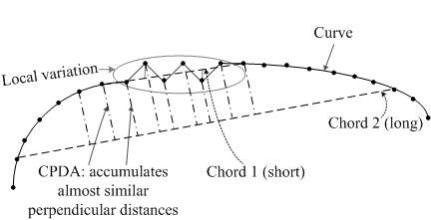
検出器は大きな近傍を使用するため、ノイズや曲線の局所的な変化の影響を受けにくくなります。CPDA検出器は、CSS検出器をさらに発展させたものです。手順：

1. Canny境界検出器を使用して、画像上の境界を見つけます。
2. .
   
   
   1. , , .
   2. T- T- .
   3. .
3. , , .
4. 3 , 3 .
5. 3 .
6. «» .
7. .
8. ( ) , .
9. T- , . [18]

結論

最新のアルゴリズムがより複雑になっていることに気付くかもしれません。ただし、HarrisおよびFAST検出器は、角度を決定するために最も一般的に使用され、計算が高速なアルゴリズムです。



Harris-Laplace、Hessian-Laplace、DoG、LoG、Harris-Affine、Hessian-Affine、Salient Regionsなどの検出器は、角度を決定できますが、ブロブ検出器（ドロップ）に起因するため、この記事では考慮されません、blob）。 [5]



また、この記事では、対象領域への応用の数が多く詳細であるため、角度を決定するためのアルゴリズムのセット全体を使い尽くしていません。アルゴリズムの中には、実用的なアルゴリズムよりも理論的な関心のあるものがあります。この記事では、文献で最もよく見られる角度を決定するための基本的なアルゴリズムについて説明します。



たとえば、次のアルゴリズムもあります（記事付き）。

1. 回転不変のDET演算子（おそらく最初の検出器の1つ）。PRボーデ。回転不変の画像演算子。 Procで IAPR1978、ページ579-583、1978。
2. 検出器キッチンローゼンフェルド。L.キッチンとA.ローゼンフェルド。グレーレベルコーナー検出。パターン認識レター、pp。95-102、1982年。
3. 検出器Wang-Brady。H.ワングとM.ブレイディ。動き推定のためのリアルタイムのコーナー検出アルゴリズム。Image and Vision Computing、vol。13：9、ページ。695-703、1995。
4. SCD（構造ベースのコーナー検出器）。フェイ・シェン、ハン・ワン。リアルタイムグレーレベルコーナー検出器。2000。
5. COP検出器（方向付けられたペアとしてのクロス）。SC Bae、IS Kweon、CD Yoo。COP：新しいコーナー検出器。パターン認識。レット。2002年。
6. Harris-StephenおよびShi-Tomasi検出器に基づく高度な検出器。リディア・フォルレンザ、パトリック・カートン、ドメニコ・アカルド、ジャンカルミン・ファサーノ、アントニオ・モッチャ。小型無人航空機システムに搭載された小型電気光学センサーのリアルタイムコーナー検出。2012年。
7. 検出器チャン。ジャン・ジュン、ティンジン・ルー、グイ・ガオ、リン・リアン。SAR画像の接合点検出アルゴリズム、2013年。

これはリスト全体ではないことに注意してください。





以下は、[2]から取られた角度検出器の比較表です。



角度検出器の比較（1-非常に悪い、2-悪い、3-満足、4-良い、5-すばらしい）。

演算子（アルゴリズム）	検出効率	ローカリゼーション	繰り返し頻度	耐ノイズ性	スピード
ボーデ	3	3	アフィン変換の場合は4、スケーリングの場合は2	2	4
モラベック	3	4	3	3	4
キッチン＆ローゼンフェルド	3	3	3	3	3
Forstner	4	4	アフィン変換の場合は5、スケーリングの場合は3	4	2
プレッシー	4	L接続角度の場合は4、その他のタイプの場合は2	アフィン変換の場合は5、異方性勾配が計算される場合は3、スケーリングの場合は3	3	2
デリチェ	3（？）	4	4	2	4
ワン＆ブレイディ	4	4	4	3	4
スーザン	4	ぼやけた画像の場合は1、それ以外の場合は4+	スケーリングの場合は4、アフィン変換の場合は2	5	4
CSS	4	4	5	4	使用される境界検出器に大きく依存
Trajkovic＆Hedley（4人の隣人）	2	4	3（ターンに対して不変ではない）	2	5
トライコビッチとヘドリー（8人の隣人）	3	4	3+（曲げに対して不変ではない）	4	5
hengと王	4	L接続角度の場合は4、その他のタイプの場合は3	アフィン変換の場合は5、スケーリングの場合は3	3	3

スミスの人工画像でのコーナー検出器の動作（スミスの合成テストパターン）。

演算子（アルゴリズム）	作業結果
モラベック[2]
プレッシー
スーザン
フォルストナー[10]
Trajkovic4
トライコビッチ8
シ・トマシ[20]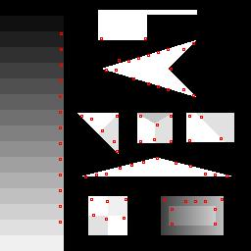

家のテスト画像でのコーナー検出器の動作（ハウステスト画像）。

演算子（アルゴリズム）	作業結果
モラベック
プレッシー
スーザン[16]
Forstner
速い[21]
オリジナルCSS [16]
拡張CSS [16]
グローバルおよびローカルの 曲率特性に基づいたコーナー検出器2008 [16]
キッチンローゼンフェルト[22]
COP [22]

PS：メインの角度検出器を確認しようとしました。私は成功したと思います。記事に誤りがある場合は、PMでメッセージを送信してください。また、一部のアルゴリズムは一般化されすぎているかもしれませんが、すべての詳細を記述した場合、記事はさらに大きくなり、ストーリーのスレッドが失われます。

参照資料

[1] Konushin A.シーンのポイントフィーチャの追跡（ポイントフィーチャトラッキング）。コンピュータグラフィックスとマルチメディア。発行番号1（5）/ 2003。

[2] Abhishak Yadav、Poonam Yadav。デジタル画像処理、2009年。

[3] Naturalでの正確な接合部検出および特性評価。

[4] 特徴点を検出する方法のレビュー。

[5] Tinne Tuytelaars、Krystian Mikolajczyk。 Local Invariant Feature Detectors：A Survey、2008.

[6] Harris Corner Detector。

[7] http://www.cs.toronto.edu/~jepson/csc420/notes/imageFeaturesIIBinder.pdf。

[8] MHミロスラフトレイコヴィー。高速コーナー検出、1998。

[9] T. Shi。追跡する優れた機能、1994。

[10] V.ロードホルスト、A。コスチャン。特徴点検出器の比較と評価、2006年。

[11] 講義13.関心点検出、2004年。

[12] B.スミス。スーザン-低レベルへの新しいアプローチ、1997。

[13] ER a。 T.ドラモンド。高性能追跡のためのポイントとラインの融合、2005年。

[14] RP a。 TDエドワードロステン。より速く、より良く：コーナー検出への機械学習アプローチ、2008。

[15] A.ラタランシ、WUMWU部。エレクター。計算工学R. Chin、平面曲線のコーナーのスケールベースの検出、パターン分析と機械知能、IEEE Transactions on（Volume：14、Issue：4）、1992.

[16]X.チェン・ヘ、N。ヨン。グローバルおよびローカル曲率に基づくコーナー検出器、2008。

[17] RS Farzin Mokhtarian。曲率スケール空間を介したロバストな画像コーナー検出、1998年。

[18] M. Awrangjeb。CPDA、2009年。

[19] SMM Kahaki、平均投影変換を使用した輪郭ベースのコーナー検出と分類、2014。

[20] COMPSCI 773特徴点検出。

[21] Andres Solis Montero、MilosStojmenović、Amiya Nayak。画像内のコーナーおよびコーナーラインリンクの堅牢な検出。コンピュータおよび情報技術に関する第10回IEEE国際会議（CIT 2010）、2010年。

[22] SC Bae、IS Kweon、およびCD Yoo。COP：新しいコーナー検出器。パターン認識。Lett。、2002年。