はじめに
すべての人に良い一日を!
皆さんの多くはすでに秘密の視覚情報の共有に興味を持っていると思います。 もしそうなら、あなたはおそらく2013年4月19日の投稿だけでなく、視覚暗号化に専念しているMoni NaorとAdi Shamirの仕事に精通しているでしょう。 この記事で提案されたMATLABで書かれたアルゴリズムと関数コードを研究しましたが、合理的に書かれていないと結論に達しました。効率を上げるだけでなく、もっと短く書けます。 これを行う方法については、以下で説明します。 整理方法も検討してください。
コードの最適化
この関数の欠点は、プログラムが同じタイプのコードを何度も繰り返すことです。これにより、関数のサイズが大きくなり、実行が複雑になりますが、MATLABで利用可能なツールにより、より短く記述できます。
getShdwImg関数コードを次のように最適化することをお勧めします。
function [S1,S2] =getShdwImgrac2x2(Img) % S1 S2 (Img) % % [m,n] = size(Img); % :) S1= zeros(2*m,2*n); S2= zeros(2*m,2*n); r1=[1 0; 1 0]; r2=[0 1; 0 1]; r3=[0 0; 1 1]; r4=[1 1; 0 0]; r5=[1 0; 0 1]; r6=[0 1; 1 0]; r=cat(3, r1, r2, r3, r4, r5, r6); % - . 1 % : for i=1:m-1 for j=1:n-1 k = randi(6); if(Img(i,j)==1) S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); else if (mod(k,2) == 0) S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k-1); else S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k+1); end end end end
ソースコードと比較して、このコードの違いを詳細に検討しましょう。
- 図1に示すピクセル状態の組み合わせを取得するように、変数r1〜r6、ディメンション2x2のセットを宣言します。この関数は、ソースコードとは異なり、6つの可能な組み合わせで機能します。
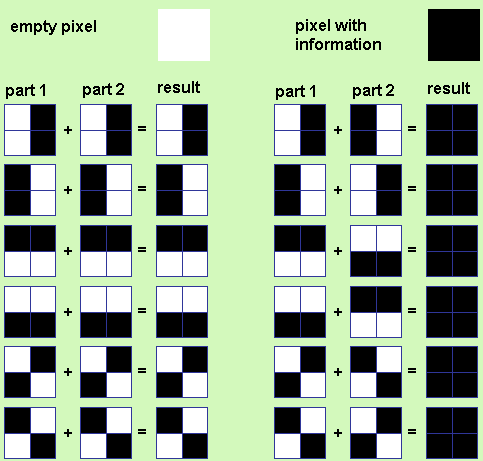
r1=[1 0; 1 0]; r2=[0 1; 0 1]; r3=[0 0; 1 1]; r4=[1 1; 0 0]; r5=[1 0; 0 1]; r6=[0 1; 1 0];
- catコマンド(3、a、b、c ...)を使用して、入力した変数を3次元配列に結合します。 コマンドの最初の属性は、最初の属性の後にリストされた配列が結合される配列の次元を示します。
r=cat(3, r1, r2, r3, r4, r5, r6);
- 変数kの整数値を1から6までランダムに生成する演算子を接続します。
k = randi(6);
- 条件演算子の中では、条件が満たされている場合、変数S1、S2を記述します。 変数rの値が割り当てられるセル。 k層r(:、:、k)を参照するため、値はランダムに生成された数kに依存します。
S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k);
- 条件が満たされない場合は、もう1つの条件付きifステートメントを接続します。 そのタスクは、変数S1、S2に割り当てられる配列レイヤーrのインデックスを変更することです。 したがって、変数kが偶数の場合、インデックスは次のように割り当てられます。
S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k-1);
それ以外の場合、レイヤーインデックスは次の式で決定されます。
S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k+1);
- 分類された視覚情報を分離するためのアルゴリズムの動作を示すMatlabスクリプトのコードを変更する必要はありません。
close all % RGB- biImg = imread('e_30.jpg'); biImg = rgb2gray(biImg); level = graythresh(biImg); % (Otsu) biImg = im2bw(biImg,level); % figure(1) imshow(biImg); title(['Original binary image']); % [S1,S2] =getShdwImgrac2x2(biImg); % figure(2) imshow(S1); title(['Shadow image S1']); % figure(3) imshow(S2); title(['Shadow image S2']); % % figure(4) %imshow(and(S1,S2)); imshow(~xor(S1, S2)); % “~”(NOT) , , title(['Superimposed image']);

ソース画像

バイナリに変換された元の画像

最初の影の画像

セカンドシャドウ画像

論理演算子〜xorを使用して2つのシャドウ画像を結合して得られた画像
次に、バイナリイメージのShamir秘密共有スキーム(3.3)の関数コードに注目します。
バイナリイメージのShamirの秘密共有スキーム(3.3)の機能コード開発
この関数は、画像を3つの影に分割することを目的としています。 元の画像は、3つすべてのシャドウ画像を組み合わせることによってのみ復元できます。 一般に、そのコードは上記のコードに似ていますが、多くの重要な追加があります。
function [S1,S2,S3] =getShdwImgrac3x3opt(Img) % % S1, S2, S3 (Img) % % [m,n] = size(Img); % 3 ) S1= zeros(2*m,2*n); S2= zeros(2*m,2*n); S3= zeros(2*m,2*n); % c01=[0 0 1 1; 0 1 0 1; 0 1 1 0]; c02=[1 0 0 1; 1 0 1 0; 0 0 1 1]; c03=[1 1 0 0; 0 1 0 1; 1 0 0 1]; c04=[0 1 1 0; 1 0 1 0; 1 1 0 0]; c0=cat(3, c01, c02, c03, c04); c05=[1 1 0 0; 1 0 1 0; 1 0 0 1]; c06=[0 1 1 0; 0 1 0 1; 1 1 0 0]; c07=[0 0 1 1; 1 0 1 0; 0 1 1 0]; c08=[1 0 0 1; 0 1 0 1; 0 0 1 1]; c1=cat(3, c05, c06, c07, c08); % 3 % for i=1:m-1 for j=1:n-1 d=randi(4); % c k = randperm(3); % if(Img(i,j)==1) S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(1),1:4,d), 2, 2); S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(2),1:4,d), 2, 2); S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(3),1:4,d), 2, 2); else S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(1,1:4, d), 2, 2); S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(2,1:4, d), 2, 2); S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(3,1:4, d), 2, 2); end end end
getShdwImgrac3x3opt関数とgetShdwImgrac2x2関数の違いを詳しく見てみましょう。
- 元の画像のサイズmは変数m、nに書き込まれ、その後、サイズ2 * m、2 * nの3つのゼロ行列が作成されます。
% [m,n] = size(Img); % 3 ) S1= zeros(2*m,2*n); S2= zeros(2*m,2*n); S3= zeros(2*m,2*n);
- この記事に基づいて、Shamiraはそれぞれ黒と白のピクセル用に4列と3行の4つの配列を開発しました。 4つの配列ごとに、4層の対応する3次元配列に結合されます。
% c01=[0 0 1 1; 0 1 0 1; 0 1 1 0]; c02=[1 0 0 1; 1 0 1 0; 0 0 1 1]; c03=[1 1 0 0; 0 1 0 1; 1 0 0 1]; c04=[0 1 1 0; 1 0 1 0; 1 1 0 0]; c0=cat(3, c01, c02, c03, c04); c05=[1 1 0 0; 1 0 1 0; 1 0 0 1]; c06=[0 1 1 0; 0 1 0 1; 1 1 0 0]; c07=[0 0 1 1; 1 0 1 0; 0 1 1 0]; c08=[1 0 0 1; 0 1 0 1; 0 0 1 1]; c1=cat(3, c05, c06, c07, c08);
- これで、元の画像の各ピクセルに対して、特定のアルゴリズムに従って4つのセルの配列が作成されます。 ソース画像のセルを循環するために、2つのサイクルが使用されます。1つはセル値を垂直に切り替え、2つ目は水平に切り替えます。
ループ内では、3次元配列のレイヤー番号を生成する整数疑似乱数ジェネレーターが使用されます。 1から3までの数のさまざまな順列が別の変数に書き込まれます。
for i=1:m-1 for j=1:n-1 d=randi(4); % c k = randperm(3); %
- 彼はモデリングを通じて、新しいマトリックスの必要なセルにアクセスするために必要な式を確立しました。 4つの各セルには、アルゴリズムのパラグラフ2でコンパイルされたマトリックスの対応する値が割り当てられます。 値を適切に割り当てるには、reshapeコマンド(c0(k(1)、1:4、d)、2、2)を使用します。
このコマンドを使用すると、既存のマトリックスを特定のサイズのマトリックスに変換できます。 したがって、最初のパラメーター-変換されるマトリックスの名前を示し、2番目と3番目のパラメーター-取得されるマトリックスのサイズを示します。 マトリックスc0のパラメーターでは、変数k(1)が行を選択します。 この場合、行番号は、ステップ3で実行されるランダム順列を実行することによって選択されます。変数dは、3次元マトリックスのレイヤーを選択する役割を果たします。 パラグラフ4でランダムに生成されます。
元の画像のピクセルの色に応じて、値はマトリックスc0またはマトリックスc1から割り当てられます。 必要なマトリックスの選択は、条件付きelse演算子によって実行されます。
条件文の終了後、終了コマンドを登録する必要があります。
if(Img(i,j)==1) S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(1),1:4,d), 2, 2); S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(2),1:4,d), 2, 2); S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(3),1:4,d), 2, 2); else S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(1,1:4, d), 2, 2); S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(2,1:4, d), 2, 2); S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(3,1:4, d), 2, 2); end end end
-
今回は、getShdwImgrac3x3opt関数を呼び出すMatlabスクリプトにも小さな変更が加えられました。
close all % RGB- biImg = imread('e_30.jpg'); biImg = rgb2gray(biImg); level = graythresh(biImg); % (Otsu) biImg = im2bw(biImg,level); % % figure(1) imshow(biImg); title([' ']); % getShdwImgrac3x3opt [S1,S2,S3] =getShdwImgrac3x3opt(biImg); % figure(2) imshow(S1); title([' ']); % figure(3) imshow(S2); title([' ']); % figure(4) imshow(S3); title([' ']); % % figure(5) S12=xor(S1, S2); S=imshow(~xor(S12, S3));% “~”(NOT) , , % title([' ']);
このスクリプトと以前のバージョンの主な違いは、追加の変数S12が作成され、そこに画像オーバーレイマトリックスS1、S2が書き込まれることです。 その後、最終結果である行列S12、S3の重ね合わせの結果が変数Sに書き込まれます。
- 同じソース画像を使用して、3つのシャドウ画像に分割します
-



影の画像
- 3つのシャドウイメージをオーバーレイした後、元のイメージが取得されました。

それを読んでくれたみんなに感謝します。 頑張って