宇宙
次のように定義された
Universe
データ型を考えます。
data Universe a = Universe [a] a [a]
これは両側の無限のリストですが、関数を使用してシフトできる要素に焦点を当てています:
left, right :: Universe a -> Universe a left (Universe (a:as) x bs) = Universe as a (x:bs) right (Universe as x (b:bs)) = Universe (x:as) b bs
本質的に、これはジッパータイプですが、無限のメモリ領域への定数Cポインターと考えることができます。インクリメントとデクリメントの操作はそれに適用できます。 しかし、それをどのように逆参照するのですか? これを行うには、フォーカスされた値を取得する関数を定義します。
extract :: Universe a -> a extract (Universe _ x _) = x
たとえば、
Universe [-1, -2..] 0 [1, 2..]
はすべて整数です。 ただし、
Universe [0, -1..] 1 [2, 3..]
は同じ整数
Universe [0, -1..] 1 [2, 3..]
が、コンテキストがわずかに変更されています(別の要素を指します)。

すべての次数2を取得する場合、関数
(2**)
を整数の
Universe
に適用する方法が必要です。 すべての法律に従うFunctorクラスのインスタンスを定義するのは簡単です:
instance Functor Universe where fmap f (Universe as x bs) = Universe (fmap f as) (fx) (fmap f bs) -- powersOf2 = fmap (2**) (Universe [-1, -2..] 0 [1, 2..]) -- ..0.25, 0.5, 1, 2, 4..
セルオートマトンでは、セルの値は前のステップの他のすべてのセルの値に依存します。 したがって、すべてのシフトの
Universe
それらの畳み込みのルールを作成できます。
duplicate :: Universe a -> Universe (Universe a) duplicate u = Universe (tail $ iterate left u) u (tail $ iterate right u)
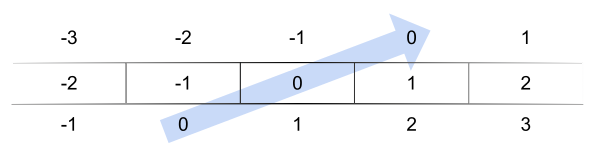
畳み込みルールは、
Universe Bool
Universe a -> a
タイプである必要があるため、
Universe Bool
の場合、ルールの例は次のようになります。
rule :: Universe Bool -> Bool rule u = lx /= cx where lx = extract $ left u cx = extract u
すべてのシフトのユニバースにルールを適用すると、オートマトンの次の状態が得られます。
next :: Universe a -> (Universe a -> a) -> Universe a next ur = fmap r (duplicate u) -- un = Universe (repeat False) True (repeat False) `next` rule

コモナド
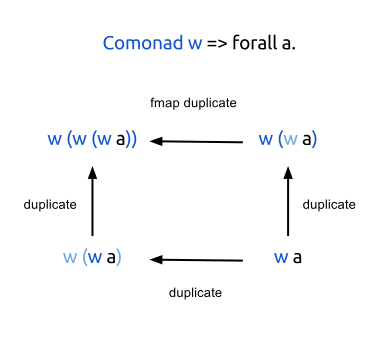
私たちの機能が以下の法律に従うことに気付くかもしれません:
extract . duplicate = id fmap extract . duplicate = id duplicate . duplicate = fmap duplicate . duplicate
したがって、
Universe
はcomonadを形成し、
next
関数は演算子
(=>>)
対応します。 小門adaはモナドの双対であり、これに関連して、操作間のいくつかの類似点を追跡できます。 たとえば、
join
はネストされたコンテキストを結合しますが、
duplicate
は逆にコンテキストを2倍にします。
return
はコンテキストに入れ、extract-そこから抽出します。
二次元セルオートマトン
これで、2次元セルオートマトンを実装できます。 最初に、2次元の
Universe
タイプを宣言し
Universe
。
newtype Universe2 a = Universe2 { getUniverse2 :: Universe (Universe a) }
Haskellでは、
fmap
コンポジションを使用してネストされたコンテナーに関数を適用するのは非常に簡単なので、
Universe2
の
Functor
クラスのインスタンスを書くことは問題ありません。
instance Functor Universe2 where fmap f = Universe2 . (fmap . fmap) f . getUniverse2
Komonadインスタンスは通常のUniverseと同じ方法で実行されます。Universe2は単なるラッパーであるため、既存のメソッドに関してメソッドを定義できます。 たとえば、
extract
は2回実行するのに十分単純です。 しかし、
duplicate
では、ネストされたコンテキストのシフトを取得する必要があり、そのためにヘルパー関数が定義されています
instance Comonad Universe2 where extract = extract . extract . getUniverse2 duplicate = fmap Universe2 . Universe2 . shifted . shifted . getUniverse2 where shifted :: Universe (Universe a) -> Universe (Universe (Universe a)) shifted u = Universe (tail $ iterate (fmap left) u) u (tail $ iterate (fmap right) u)
それがほとんどすべてです! ルールを決定し、
(=>>)
を使用して適用するためだけに残ります。 Game of Lifeでは、セルの新しい状態は隣接するセルの状態に依存するため、それらの場所の機能を定義します。
nearest3 :: Universe a -> [a] nearest3 u = fmap extract [left u, u, right u] neighbours :: (Universe2 a) -> [a] neighbours u = [ nearest3 . extract . left , pure . extract . left . extract , pure . extract . right . extract , nearest3 . extract . right ] >>= ($ getUniverse2 u)
ルール自体は次のとおりです。
data Cell = Dead | Alive deriving (Eq, Show) rule :: Universe2 Cell -> Cell rule u | nc == 2 = extract u | nc == 3 = Alive | otherwise = Dead where nc = length $ filter (==Alive) (neighbours u)
退屈な結論だけが残っているので、別に考えません。
おわりに
したがって、
rule
関数を定義するだけで、任意のセルラーオートマトンを実装できます。 遅延計算のおかげで、無限のフィールドが贈り物として得られますが、線形メモリ消費などの問題が発生します。
実際には、無限リストの各要素にルールを適用して、まだアクセスされていないセルを計算するため、前のすべての手順を実行する必要があります。つまり、それらはメモリに保存する必要があります。
両方のファイルのソースコード:
Universe.hs
module Universe where import Control.Comonad data Universe a = Universe [a] a [a] newtype Universe2 a = Universe2 { getUniverse2 :: Universe (Universe a) } left :: Universe a -> Universe a left (Universe (a:as) x bs) = Universe as a (x:bs) right :: Universe a -> Universe a right (Universe as x (b:bs)) = Universe (x:as) b bs makeUniverse fl fr x = Universe (tail $ iterate fl x) x (tail $ iterate fr x) instance Functor Universe where fmap f (Universe as x bs) = Universe (fmap f as) (fx) (fmap f bs) instance Comonad Universe where duplicate = makeUniverse left right extract (Universe _ x _) = x takeRange :: (Int, Int) -> Universe a -> [a] takeRange (a, b) u = take (b-a+1) x where Universe _ _ x | a < 0 = iterate left u !! (-a+1) | otherwise = iterate right u !! (a-1) instance Functor Universe2 where fmap f = Universe2 . (fmap . fmap) f . getUniverse2 instance Comonad Universe2 where extract = extract . extract . getUniverse2 duplicate = fmap Universe2 . Universe2 . shifted . shifted . getUniverse2 where shifted :: Universe (Universe a) -> Universe (Universe (Universe a)) shifted = makeUniverse (fmap left) (fmap right) takeRange2 :: (Int, Int) -> (Int, Int) -> Universe2 a -> [[a]] takeRange2 (x0, y0) (x1, y1) = takeRange (y0, y1) . fmap (takeRange (x0, x1)) . getUniverse2
Life.hs
import Control.Comonad import Control.Applicative import System.Process (rawSystem) import Universe data Cell = Dead | Alive deriving (Eq, Show) nearest3 :: Universe a -> [a] nearest3 u = fmap extract [left u, u, right u] neighbours :: (Universe2 a) -> [a] neighbours u = [ nearest3 . extract . left , pure . extract . left . extract , pure . extract . right . extract , nearest3 . extract . right ] >>= ($ getUniverse2 u) rule :: Universe2 Cell -> Cell rule u | nc == 2 = extract u | nc == 3 = Alive | otherwise = Dead where nc = length $ filter (==Alive) (neighbours u) renderLife :: Universe2 Cell -> String renderLife = unlines . map concat . map (map renderCell) . takeRange2 (-7, -7) (20, 20) where renderCell Alive = "██" renderCell Dead = " " fromList :: a -> [a] -> Universe a fromList d (x:xs) = Universe (repeat d) x (xs ++ repeat d) fromList2 :: a -> [[a]] -> Universe2 a fromList2 d = Universe2 . fromList ud . fmap (fromList d) where ud = Universe (repeat d) d (repeat d) cells = [ [ Dead, Alive, Dead] , [Alive, Dead, Dead] , [Alive, Alive, Alive] ] main = do gameLoop $ fromList2 Dead cells gameLoop :: Universe2 Cell -> IO a gameLoop u = do getLine rawSystem "clear" [] putStr $ renderLife u gameLoop (u =>> rule)
この記事を手伝ってくれたint_indexに感謝します。