すでに木を構築していると想像してください
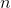 キーを取得し、指定されたキーがツリーにあるかどうかのリクエストに応答する必要があります。 ユーザーは主に1つのキーに興味があり、残りのキーはときどきしか求めないことがわかります。 キーがルートから遠く離れている場合、
キーを取得し、指定されたキーがツリーにあるかどうかのリクエストに応答する必要があります。 ユーザーは主に1つのキーに興味があり、残りのキーはときどきしか求めないことがわかります。 キーがルートから遠く離れている場合、 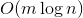 時間。 常識は、スコアを最適化できることを示します
時間。 常識は、スコアを最適化できることを示します 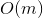 ツリーにキャッシュを追加します。 しかし、このアプローチには柔軟性と優雅さが欠けています。
ツリーにキャッシュを追加します。 しかし、このアプローチには柔軟性と優雅さが欠けています。
今日はスプレーツリーについてお話します。 これらのツリーは永続的にバランスが取れておらず、線形時間でさえ個別のリクエストで機能します。 ただし、各リクエストの後に構造が変更されるため、頻繁に繰り返されるリクエストを非常に頻繁に処理できます。 さらに、それらからの1つのリクエストを処理する減価償却費
 、スプレイツリーは永続的にバランスの取れた同等物の優れた代替手段になります。
、スプレイツリーは永続的にバランスの取れた同等物の優れた代替手段になります。
スプレイツリー
80年代半ば、ロバートタージャンとダニエルスレーターは、美しく効率的なデータ構造を提案しました。 それらはすべて単純な基本構造と、ローカルで常に修正する1つまたは2つのヒューリスティックを備えています。 スプレイツリーはそのような構造の1つです。
スプレイツリーは、自己バランス型のバイナリ検索ツリーです。 ツリーは追加情報を保存する必要がないため、メモリ効率が良くなります。 各呼び出しの後、検索でも、スプレイツリーはその構造を変更します。
以下では、ペアごとに異なるキーのセットでツリーがどのように機能するかのアルゴリズムを説明し、それを分析します。
アルゴリズム
ツリーの構造を記述するには、単一の頂点を記述する単純なクラスが必要です。
class Node: def __init__(self, key, left = None, right = None, parent = None): self.left = left self.right = right self.parent = parent self.key = key
そして、親へのポインタを操作するための2つのサポート手順。
def set_parent(child, parent): if child != None: child.parent = parent def keep_parent(v): set_parent(v.left, v) set_parent(v.right, v)
スプレイツリーの主なヒューリスティックは、ルートへの移動です。 頂点にアクセスした後、ルートに到達します。 登山は、山の曲がり角によって実現されます。 次の図に示すように、1つのターンで、親を子と交換できます。

def rotate(parent, child): gparent = parent.parent if gparent != None: if gparent.left == parent: gparent.left = child else: gparent.right = child if parent.left == child: parent.left, child.right = child.right, parent else: parent.right, child.left = child.left, parent keep_parent(child) keep_parent(parent) child.parent = gparent
しかし、トップになるだけでルートになるだけでは不十分です。 スプレイツリーの秘isは、頂点を上に移動すると、ルートまでの距離が、上昇している頂点だけでなく、現在のサブツリーのすべての子孫についても短くなることです。 このために、ジグジグおよびジグザグのコーナリング手法が使用されます。
ジグジグとジグザグターンの基本的な考え方は、祖父から子供への道を考えることです。 パスが左の子のみまたは右のみに沿って進む場合、この状況はジグジグと呼ばれます。 下図に処理方法を示します。 最初に親を、次に子を回します。
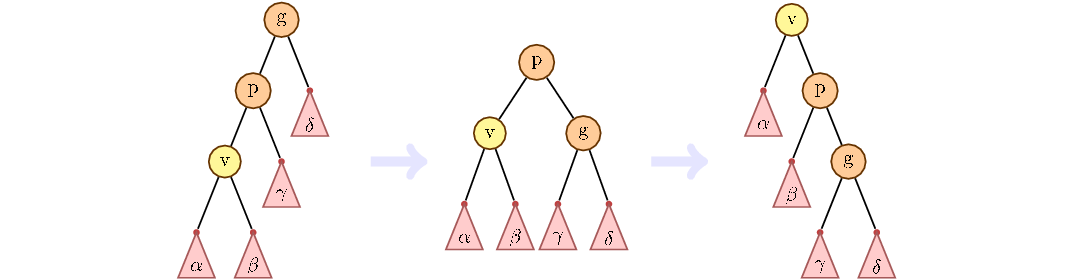
そうでない場合は、まず現在の親で子を変更し、次に新しい親で変更します。

上部に祖父がいない場合、通常のターンを行います。

上記のzig-zigおよびzig-zagターンを使用して頂点を上げる手順は、スプレイツリーの鍵です。
ご注意 ロシア語では、「スプレイ」という用語は「エキスパンド」と翻訳されました。 これはあまり良い翻訳ではないと思います。 あなたはトップを取り、それを引き上げます。 この時点で、他のすべてのピークは下がり、向きを変えます。 Tシャツをひねると似たようなことが起こります。 したがって、ここでは「ねじれ」という言葉がより適切であると思われます。
def splay(v): if v.parent == None: return v parent = v.parent gparent = parent.parent if gparent == None: rotate(parent, v) return v else: zigzig = (gparent.left == parent) == (parent.left == v) if zigzig: rotate(gparent, parent) rotate(parent, v) else: rotate(parent, v) rotate(gparent, v) return splay(v)
スプレイツリーの検索手順は、最後の段階でのみ通常の検索手順と異なります。頂点が見つかったら、それをプルアップし、
splay
手順でルートにします。
def find(v, key): if v == None: return None if key == v.key: return splay(v) if key < v.key and v.left != None: return find(v.left, key) if key > v.key and v.right != None: return find(v.right, key) return splay(v)
キーの挿入と削除を実装するには、
split
と
merge
(切り取りとマージ)の2つの手順が必要です。
split
プロシージャは、キーキーを入力として受け取り、ツリーを2つに分割します。 1つのツリーでは、すべての値が
key
より小さく、別のツリーではそれより大きくなります。 簡単に実装されます。 キーに最も近い頂点を
find
し、それを上に伸ばしてから、左または右のサブツリー(またはその両方)を切り取る必要があり
find
。
def split(root, key): if root == None: return None, None root = find(root, key) if root.key == key: set_parent(root.left, None) set_parent(root.right, None) return root.left, root.right if root.key < key: right, root.right = root.right, None set_parent(right, None) return root, right else: left, root.left = root.left, None set_parent(left, None) return left, root
次のキーを挿入するには、その上で
split
を呼び出してから、新しい頂点ルートを作成するだけで十分です。サブツリーは
split
結果になります。
def insert(root, key): left, right = split(root, key) root = Node(key, left, right) keep_parent(root) return root
merge
プロシージャは、入力でleft
left
とright
right
2つのツリーを受け取ります。 正常に動作するには、
left
ツリーのキーが
right
ツリーのキーよりも小さくなければなりません。 ここで、右のツリーの最小のキーを持つ頂点を
right
、上にドラッグします。 その後、左のサブツリーとして、
left
ツリーに参加します。
def merge(left, right): if right == None: return left if left == None: return right right = find(right, left.key) right.left, left.parent = left, right return right
頂点を削除するには、頂点を上げてから、左右のサブツリーをマージする必要があります。
def remove(root, key): root = find(root, key) set_parent(root.left, None) set_parent(root.right, None) return merge(root.left, root.right)
スプレイツリーで重複キーをサポートするには、2つの方法があります。 各キーに、必要な追加物を保存するリストを関連付ける必要があります。 または、検索プロシージャを実装して、指定されたキー以上のキーを持つLURトラバーサル順序の最初の頂点を返します。
分析
ツリーの削除、挿入、マージ、および分割が機能することに注意してください
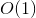 +
+ find
手順のランタイム。
find
手順は、ツリー内の目的の頂点の深さに比例して機能します。 検索が
splay
と、
splay
手順が
splay
されます。これは、頂点の深さに比例して機能します。 したがって、
splay
プロシージャの実行時間を評価するだけで十分です。
分析には、物理学者の方法を使用します 。これについては、 減価償却分析に関する記事で説明しました。 させて
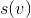 -サブツリーサイズ
-サブツリーサイズ 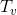 上部にルートがある
上部にルートがある 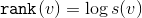 。 私たちの可能性は
。 私たちの可能性は 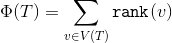 。
。
splay(v)
プロシージャの実際の時間は深度に等しいと仮定します
声明 上からの
splay
操作の償却費
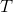 ルート付き
ルート付き 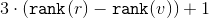 。
。
証明 。
もし
splay(v)
をステップに分割します。 各ステップ中に、ジグ、ジグジグ、またはジグザグの3つのターンのいずれかが実行されます。 時間単位は、ジグジグとジグザグの2単位の単純なターンに費やされます。
各ステージの後、トップのランク
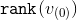 そして後
そして後 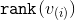 。 おそらく最後を除いて、各段階について、その実装のための減価償却時間は上から制限できることを示します。
。 おそらく最後を除いて、各段階について、その実装のための減価償却時間は上から制限できることを示します。 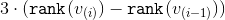 。 最終段階では、上限は
。 最終段階では、上限は 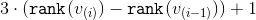 。 上限を合計し、ランクの中間値を減らすと、必要な値が得られます
。 上限を合計し、ランクの中間値を減らすと、必要な値が得られます
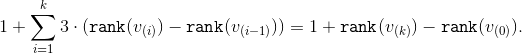
あなたはただそれに注意する必要があります
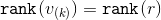 、そして
、そして 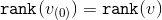 。
。
次に、各タイプの回転を個別に分析します。
ジグ 最後の段階で一度だけ実行できます。 実時間
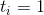 。 図を見て、ランクが頂点でのみ変化することを理解しましょう
。 図を見て、ランクが頂点でのみ変化することを理解しましょう 
したがって、減価償却費は
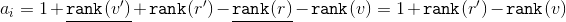 。 成績
。 成績  そして
そして  減少しています。 対応するサブツリーのサイズに基づいて、式に適用します
減少しています。 対応するサブツリーのサイズに基づいて、式に適用します 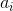 不等式:
不等式:
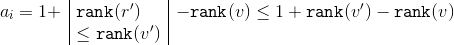
手段
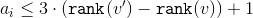 。
。
ジグジグ 実時間
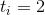 。 ランクは頂点でのみ変化することに注意してください
。 ランクは頂点でのみ変化することに注意してください  、
、 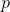 そして
そして 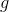 。
。

次に減価償却費
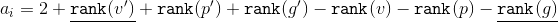 。 成績
。 成績  そして
そして 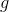 短縮できます。 わかった
短縮できます。 わかった 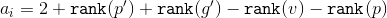 。 サブツリーのサイズに基づいて、式に適用します
。 サブツリーのサイズに基づいて、式に適用します 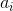 2つの不等式:
2つの不等式:
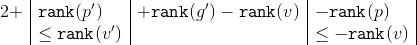
そしてそれを得る
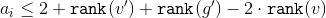 。
。
私たちの目標はそれを示すことです
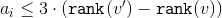 。 このためには、それを示すのに十分です
。 このためには、それを示すのに十分です 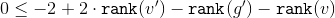 :
:

便宜上、ランクを左側に移し、証明します
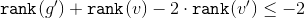 。 ランクの定義により
。 ランクの定義により 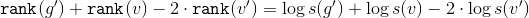 。 最後の平等
。 最後の平等 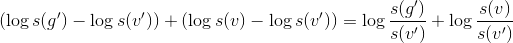 。 図を見て、それを理解しましょう
。 図を見て、それを理解しましょう  。
。
事実
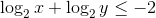 肯定的な
肯定的な 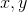 そのような
そのような 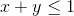 。
。
手段
 。 必要なものを得ました。
。 必要なものを得ました。
ジグザグ

前のケースと同様に、減価償却の見積もりを記述します。
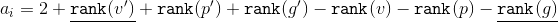 。
。
成績
 そして
そして 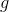 減少しています。 式へ
減少しています。 式へ 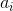 次の不等式を適用します。
次の不等式を適用します。
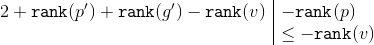
手段
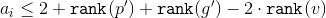 。 この不等式は、前のケースと同様に証明されます。
。 この不等式は、前のケースと同様に証明されます。
したがって、3つのケースすべてを分析し、ランク全体の償却時間の上限を受け取りました。

頂点のランクはツリーサイズの対数によって制限されることに注意してください。 そこから次の定理が続きます。
定理
splay
減価償却されます
 。
。
その他のメトリックとプロパティ
デザートについては、 ウィキペディアを参照して、
splay
ツリーに関する興味深い事実をいくつか紹介します。
静的最適性定理 。 させて
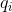 -アイテムがリクエストされた回数
-アイテムがリクエストされた回数 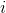 。 それから
。 それから 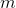
splay
ツリーの検索クエリが実行される
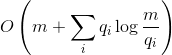 。
。
実際、この事実は次のことを報告しています。 さまざまな要素に対していくつのクエリが要求されるかを事前にお知らせください。 これらの要求に可能な限り迅速に応答するために、特定のバイナリツリーを構築しています。 ステートメントは、
splay
定数に対して正確
splay
ツリーは私たちが考えることができる最も最適な固定ツリーよりも悪化しないことを述べています。
現在のセットの定理 。 させて
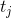 -これは、要素への最後のリクエスト以降にすでに行ったリクエストの数です
-これは、要素への最後のリクエスト以降にすでに行ったリクエストの数です 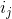 ; まだ対処していない場合は、最初からのリクエストの数だけです。 次に処理時間
; まだ対処していない場合は、最初からのリクエストの数だけです。 次に処理時間 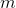 リクエストは
リクエストは 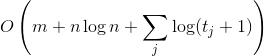 。
。
この事実は、記事の冒頭でのキャッシュについての私の議論を形式化します。 実際、彼は平均して、最近リクエストされたアイテムはルートから浮かないと言います。
スキャン定理
splay
ツリーの要素への順次アクセス(LUR)は、
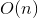 。
。
この事実は大きな実用的な結果をもたらします。 分割およびマージ操作とともに、
splay
ツリーは
rope
データ構造の優れた基盤となります。 それについては、Habr Ropesの投稿で読むことができます-高速回線とモノイドとそのアプリケーション....
ご清聴ありがとうございました!
文学
- タージャン「データ構造とネットワークアルゴリズム」
- スリーター、ダニエルD。; タージャン、ロバートE.(1985)、「自己調整バイナリ検索ツリー」
UPD
語用論
このアルゴリズムの実際の適用性についてのコメントには、合理的な疑問があります。 それに答える前に、この投稿が最初に読者にアルゴリズム自体とその理論的基礎を紹介していることに注意したい。 このため、効果的な実装、詳細、および最適化の秘aboutについての質問がありますが、それらは多くありますが、この記事では省略しました。
スプレイツリーのパフォーマンスと範囲の研究は、12の記事のトピックであることが判明しました。 20個のバランスの取れたツリーをノードのさまざまな内部表現と比較する「システムソフトウェアのBSTのパフォーマンス分析」のPfaffのレビューは、非常に楽観的です。 テストは、仮想メモリの管理、IPパケットのキャッシュ、相互参照の解決などのタスクの実データで実行されます。 仮想メモリと相互参照では、スプレイツリーのパフォーマンスが最高でした。 IPパケットはAVLおよび赤黒木に取って代わりました。 高性能は、実際のデータの機能によって説明されます。 研究の詳細は、記事自体で読むのが最適です。
また、Timi Ahoなどの記事「Timing Aplaying and Advantage of Working Sets」で、スプレイツリーのパフォーマンスとターン数を減らす問題に関するレポートを詳しく読むことができます。 記事の最後にある参考文献には、さらにいくつかのパフォーマンスレポートが含まれています。