アルゴリズムの複雑性分析の概要（パート1）

翻訳者から：このテキストは、材料を過度に「噛む」場所のために、小さな略語で示されています。 著者は、特定のトピックがあまりにも単純または有名すぎるように見えることを正しく警告しています。 それにもかかわらず、個人的には、このテキストは、アルゴリズムの複雑さの分析に関する既存の知識を合理化するのに役立ちました。 他の誰かに役立つことを願っています。

元の記事の量が多いため、私はそれを部分に分割しましたが、そのうち合計4つになります。

私は（いつものように）翻訳の品質の改善に関するPMのコメントに非常に感謝します。

はじめに

クールで普及したプログラムを書く現代のプログラマーの多くは、理論的なコンピューターサイエンスの非常に曖昧な考えを持っています。 これは、彼らが優秀なクリエイティブスペシャリストであり続けることを妨げるものではありません。彼らが作成したものに感謝しています。



ただし、理論の知識にも利点があり、非常に有用です。 この記事は、優れた実践者であるが理論の理解が不十分なプログラマーを対象に、最も実用的なプログラミングツールの1つ、「ビッグO」表記法とアルゴリズムの複雑さの分析を紹介します。 学術科学の分野と商用ソフトウェアの作成の両方で働いた人として、私はこれらのツールが実際に非常に役立つと思います。 この記事を読んだ後、それをあなた自身のコードに適用して、さらに改善できることを願っています。 また、この投稿では、「ビッグO」、「漸近的振る舞い」、「最悪の場合の分析」など、コンピューターサイエンスの理論家が使用する一般的な用語の理解をもたらします。



このテキストは、ギリシャまたはコンピューターサイエンスの国際オリンピックに参加している他の国の高校生、学生のアルゴリズムの競争なども対象としています。 そのため、複雑な数学的問題に関する予備知識は不要であり、アルゴリズムのさらなる研究の基礎を提供し、それらの背後にある理論をしっかりと理解します。 かつてさまざまなコンテストにたくさん参加した人として、入門資料をすべて読んで理解することを強くお勧めします。 この知識は、アルゴリズムとさまざまな高度な技術を引き続き学習する場合に不可欠です。



このテキストが、理論的なコンピューターサイエンスの経験があまりない実践的なプログラマーに役立つことを願っています（最も刺激を受けたソフトウェアエンジニアが大学に進学したことがないという事実は長年の事実です）。 しかし、この記事は学生も対象としているため、時には教科書のように聞こえます。 さらに、一部のトピックはあなたには単純すぎるように見えるかもしれません（例えば、トレーニング中にそれらに遭遇したかもしれません）。 あなたがそれらを理解していると感じたら、これらの点をスキップしてください。 競技に参加する学生は、平均的な実践者よりもアルゴリズム理論をよりよく理解する必要があるため、他のセクションは少し深く、より理論的になります。 しかし、これらのことを知ることはそれほど有用ではなく、物語の経過をたどることはそれほど難しくないので、おそらくあなたの注意に値するでしょう。 元のテキストは高校生に送信されたため、特別な数学的知識は必要ないため、プログラミングの経験がある人（たとえば、再帰とは何か）は問題なく理解できます。



この記事では、議論の範囲を超えた資料への多くの興味深いリンクを見つけるでしょう。 あなたがプログラマーである場合、これらの概念のほとんどに精通している可能性があります。 コンテストに参加する初心者の学生の場合、これらのリンクをクリックすると、まだ研究していないコンピューターサイエンスとソフトウェア開発の他の分野に関する情報が得られます。 それらを参照して、自分の知識を増やしてください。



「Big O」表記法とアルゴリズムの複雑さの分析は、実用的なプログラマーと初心者の学生の両方が、役に立たないと理解するのが難しい、恐れる、または一般的に回避されることが多いことです。 しかし、それらは一見すると思われるほど複雑で難解ではありません。 アルゴリズムの複雑さは、プログラムまたはアルゴリズムの動作速度を正式に測定するための単なる方法であり、これは非常に実用的な目標です。 このトピックに関する少しの動機付けから始めましょう。

やる気

コードの動作速度を測定するツールがあることはすでにわかっています。 これらはプロファイラーと呼ばれるプログラムで、実行時間をミリ秒単位で決定し、ボトルネックを特定して最適化します。 しかし、それは便利なツールですが、アルゴリズムの複雑さに関係していません。 アルゴリズムの複雑さは、理想的なレベルでの2つのアルゴリズムの比較に基づいており、プログラミング言語の実装、プログラムが実行されているハードウェア、またはこのCPUのコマンドセットなどの低レベルの詳細を無視することです。 実際には、アルゴリズムを、それらが何であるかという観点で比較したいと思います。計算がどのように行われるかについてのアイデアです。 ここではミリ秒をカウントしてもあまり役に立ちません。 低レベルの言語（たとえば、 assembler ）で書かれた悪いアルゴリズムは、高レベルのプログラミング言語（たとえば、 PythonやRuby ）で書かれた良いアルゴリズムよりもはるかに高速であることが判明するかもしれません。 それで、「最良のアルゴリズム」が実際に何であるかを決定する時が来ました。



アルゴリズムは純粋に計算的なプログラムであり、ネットワークタスクやユーザーI / Oなど、コンピューターによって頻繁に実行されることはありません。 複雑さの分析により、このプログラムが計算を実行するときの速度を知ることができます。 純粋な計算操作の例としては、 浮動小数点数の操作（加算と乗算）、RAMにあるデータベースから特定の値を検索、人工知能（AI）を使用してキャラクターの動きを決定し、ゲーム内で短い距離だけ移動するようにしますまたは、文字列に一致する正規表現パターンを起動します。 明らかに、コンピューティングはコンピュータープログラムのいたるところにあります。



複雑さの分析により、入力データストリームが増加したときのアルゴリズムの動作を説明することもできます。 入力で1000個の要素を使用してアルゴリズムを1秒間実行する場合、この値を2倍にするとどうなりますか？ また、高速で動作しますか、1.5倍速くなりますか、4倍遅くなりますか？ プログラミングの実践では、このような予測は非常に重要です。 たとえば、1,000人のユーザーで動作するWebアプリケーション用のアルゴリズムを作成し、その実行時間を測定し、複雑性分析を使用すると、ユーザー数が2,000に増えたときに何が起こるかがかなりわかります。 アルゴリズムの構築における競争については、複雑性分析により、コードが正確性を検証するために最大のテストで実行される時間の長さも理解できます。 したがって、少量の入力データでプログラムの一般的な動作を決定すると、大量のデータフローでプログラムに何が起こるかを知ることができます。 簡単な例から始めましょう：配列の最大要素を見つける。

カウント命令

この記事では、さまざまなプログラミング言語を使用して例を実装します。 それらのどれにも精通していなくても心配しないでください-プログラミングができる人なら誰でも問題なくこのコードを読むことができます。それは単純であり、実装言語のエキゾチックなつまらないものを使用しないからです。 あなたがオリンピアードの学生なら、ほとんどの場合C ++で書いてください。 この場合、C ++を使用して演習を行い、さらに練習することをお勧めします。



配列の最大要素は、最も単純なコードスニペットを使用して見つけることができます。 たとえば、 Javascriptで記述されたもの。 サイズn



入力配列



与えられたn



：

 var M = A[ 0 ]; for ( var i = 0; i < n; ++i ) { if ( A[ i ] >= M ) { M = A[ i ]; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初に、ここで計算される基本命令の数を計算します。 一度だけこれを行います-理論を深く掘り下げると、そのような必要性はなくなります。 しかし、今のところ、私たちがそれに費やす時間に我慢してください。 このコードを分析する過程で、コードを単純な命令に分割することは理にかなっています。これは、プロセッサがすぐにまたはそれに近いところで実行できるタスクです。 プロセッサが次の操作を単一の命令として実行できると仮定します。

• 変数に値を割り当てる
• 配列内の特定の要素の値を見つける
• 2つの値を比較する
• 増分値
• 基本的な算術演算（例：加算および乗算）

分岐（ if



条件の計算後のコードのelse



部分とelse



部分の選択）は瞬間的であると仮定し、計算の際にこの命令を考慮しません。 上記のコードの最初の行の場合：

 var M = A[ 0 ];
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

A[0]



を検索し、 M



値を割り当てるための2つの指示が必要です（ n



常に少なくとも1であると仮定します）。 これらの2つの命令は、 n



の値に関係なく、アルゴリズムに必要です。 for



ループも継続的に初期化され、さらに2つのコマンドが割り当てられます：割り当てと比較。

 i = 0; i < n;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これはすべて、 for



の最初の実行前に発生for



ます。 新しい反復のたびに、さらに2つの命令がありますi



インクリメントと、ループを停止する時間かどうかをチェックする比較です。

 ++i; i < n;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、ループの本体の内容を無視する場合、このアルゴリズムの命令の数は4 + 2n



- for



ループの開始時に4つ、各反復に2つあり、そのうちn



個です。 ここで、 n



がわかれば、アルゴリズムに必要な命令の数がわかるように数学関数f(n)



を定義できます。 空の本体を持つforループの場合、 f( n ) = 4 + 2n



。

最悪のケース分析

ループの本体には、配列内の検索操作と常に発生する比較があります。

 if ( A[ i ] >= M ) { ...
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ただし、 if



本体は、配列の実際の値に応じて開始する場合と開始しない場合があります。 A[ i ] >= M



が発生しA[ i ] >= M



場合、2つの追加コマンドを実行します。配列内の検索と割り当て：

 M = A[ i ]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

命令の数がn



だけでなく特定の入力値にも依存するようになったため、 f(n)



それほど簡単に決定できなくなりました。 たとえば、 A = [ 1, 2, 3, 4 ]



プログラムにはA = [4、3、2、1 A = [ 1, 2, 3, 4 ]



場合よりも多くのコマンドが必要です。 アルゴリズムを分析するとき、最悪の場合のシナリオを考慮することがほとんどです。 私たちの場合はどうなりますか？ アルゴリズムを完了するために最も多くの指示が必要になるのはいつですか？ 回答： A = [ 1, 2, 3, 4 ]



ように、配列が昇順で並べられている場合。 その後、 M



が毎回再割り当てされ、最大数のチームが与えられます。 理論家はこれに対して奇妙な名前を持っています- 最も不利なケースの分析は、最も失敗したオプションの単なる検討に過ぎません。 したがって、最悪の場合、ループの本体でコードから4つの命令が起動され、 f( n ) = 4 + 2n + 4n = 6n + 4



ます。

漸近的挙動

上記で取得した関数を使用すると、アルゴリズムの速度が非常によくわかります。 しかし、私が約束したように、プログラムでチームを数えるなどの退屈なタスクを常に行う必要はありません。 さらに、使用するプログラミング言語の各規定を実装するために必要な特定のプロセッサーの命令数は、その言語のコンパイラーと使用可能な命令セット（パーソナルコンピューターのAMDまたはIntel Pentium、Playstation 2のMIPSなど）に依存します。 前に、この種の条件を無視するつもりであると言いました。 したがって、関数f



を「フィルター」に渡して、理論家が注意を払わないことを好むマイナーな詳細をクリアします。



6n + 4



関数は、 6n



と4



2つの要素で構成されています。 複雑さを分析する場合、 n



大幅に増加した命令をカウントする機能で何が起こっているのかだけn



重要です。 これは、「最悪のシナリオ」という以前の考え方と一致します。私たちは、何か困難なことをせざるを得ないときに「悪い状態」にあるアルゴリズムの動作に興味があります。 これは、アルゴリズムを比較するときに非常に役立つことに注意してください。 それらの1つが大きい入力データストリームで他の1つに勝っている場合、それはより高速で、小さくて軽いストリームにとどまる可能性があります。 それが、 n



増加とともにゆっくり増加する関数の要素を捨て、強く成長する要素だけを残す理由です。 明らかに、 n



の値に関係なく4は4のまま6n



反対に6n



は増加します。 したがって、最初に行うことは4をドロップし、 f( n ) = 6n



のみにします。



4を単に「初期化定数」と考えるのは理にかなっています。 プログラミング言語が異なると、設定に時間がかかる場合があります。 たとえば、Javaは最初に仮想マシンを初期化する必要があります。 そして、プログラミング言語の違いを無視することに同意したので、この値を単に破棄します。



無視できる2番目のことは、 n



前の要因です。 したがって、関数はf( n ) = n



ます。 ご覧のとおり、これにより作業が非常に簡単になります。 繰り返しますが、異なるプログラミング言語（PL）間のコンパイル時間の違いについて考える場合、定数の要素を破棄することは理にかなっています。 あるPLの「配列検索」は、別のPLとはまったく異なる方法でコンパイルできます。 たとえば、Cでは、 A[ i ]



実行には、 i



が宣言された配列のサイズを超えないことの確認は含まれませんが、 Pascalの場合は存在します。 したがって、このPascalコード：

 M := A[ i ]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Cの以下と同等：

 if ( i >= 0 && i < n ) { M = A[ i ]; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そのため、さまざまなプログラミング言語が、命令数に影響するさまざまな要因の影響を受けることを期待するのは理にかなっています。 この例では、最適化の機会を無視する「ダム」Pascalコンパイラを使用していますが、Cの1つではなく、配列要素へのアクセスごとに3つのPascal命令が必要です。 この要因を無視することは、特定のプログラミング言語間の違いを無視するという主流であり、アルゴリズム自体のアイデアそのものの分析に焦点を当てています。



上記のフィルター（「すべての因子をドロップする」および「最大要素のみを残す」）は、ともに漸近的挙動と呼ばれるものを提供します。 f( n ) = 2n + 8



、関数f( n ) = n



で記述されます。 数学の言語では、 n



が無限大になる傾向があるため、関数f



限界に興味があります。 この正式なフレーズの意味を十分に理解していなくても心配する必要はありません。必要なものはすべてわかっています。 （余談：厳密に言えば、数学的定式化では限界の定数を破棄することはできませんでしたが、理論的な情報学の目的のために、上記の理由でこれを行います）。 この概念を完全に理解するために、いくつかのタスクを実行してみましょう。



定数因子を破棄し、最も成長の速い要素のみを残すという原則を使用して、次の例の漸近線を見つけます。

1. f( n ) = 5n + 12
   
   
   
   はf( n ) = n
   
   
   
   を与えます。
   
   根拠は上記と同じです。
2. f( n ) = 109
   
   
   
   はf( n ) = 1
   
   
   
   ます。
   
   109 * 1
   
   
   
   で係数を落としますが、関数がゼロではないことを示すには1が必要です
3. f( n ) = n
   
   
   
   ² + 3n + 112
   
   
   
   はf( n ) = n
   
   
   
   ²を与える
   
   ここで、 n
   
   
   
   ²は3n
   
   
   
   より速く成長し、 3n
   
   
   
   は112
   
   
   
   より速く成長します
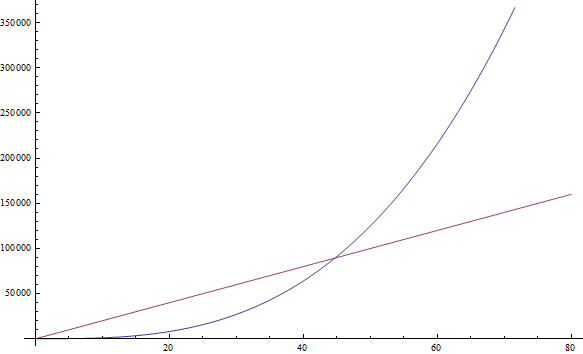
4. f( n ) = n
   
   
   
   ³ + 1999n + 1337
   
   
   
   はf( n ) = n
   
   
   
   ³を与える
   
   n
   
   
   
   前の因子の値は大きいにもかかわらず、さらに大きいn
   
   
   
   見つけることができると信じているため、 f( n ) = n
   
   
   
   ³は1999n
   
   
   
   よりも1999n
   
   
   
   （上記の図を参照）
5. f( n ) = n + sqrt( n )
   
   
   
   はf( n ) = n
   
   
   
   
   
   引数がsqrt( n )
   
   
   
   よりも速く成長するにつれてn
   
   
   
   が増加するため